基于sinh-sigmoidal組合式變換的薄型結(jié)構(gòu)邊界元分析方法*

張亞萍

(泰州職業(yè)技術(shù)學(xué)院 智能制造學(xué)院,江蘇 泰州 225300)

0 引 言

作為一種可拆卸的靜密封連接結(jié)構(gòu),墊片-法蘭-螺栓連接是石油管道及化工設(shè)備中必不可少的重要部件,目前已被廣泛應(yīng)用于機(jī)床裝備、航天航空等眾多工業(yè)領(lǐng)域[1-4]。

結(jié)構(gòu)的密封性能直接影響工業(yè)生產(chǎn)安全和企業(yè)生產(chǎn)利益。墊片作為連接結(jié)構(gòu)中的重要密封元件,其彈性力學(xué)性能也受到了普遍關(guān)注。

常見的密封方式是通過對(duì)上法蘭中的螺栓墊片施加預(yù)緊力。隨著所受預(yù)緊力的逐漸增大,墊片在受壓后,會(huì)表現(xiàn)出高度的非線性與復(fù)雜的時(shí)滯性。因此,準(zhǔn)確評(píng)估初始預(yù)緊力及最大位移載荷下的壓縮回彈性能是保證其密封性能的重要前提[5]。

研究者們一直致力于厘清影響墊片-法蘭-螺栓連接結(jié)構(gòu)密封性能及連接可靠性的影響因素,并不斷優(yōu)化靜密封連接結(jié)構(gòu)設(shè)計(jì)的計(jì)算方法和相應(yīng)的試驗(yàn)標(biāo)準(zhǔn),以期建立起嚴(yán)謹(jǐn)有效的連接設(shè)計(jì)體系。歐美和日本等國家和地區(qū)已經(jīng)建立了基于泄漏率的墊片參數(shù)以及墊片壓縮回彈性能試驗(yàn)方法,并形成了相應(yīng)的體系標(biāo)準(zhǔn)[6-8]。這套體系標(biāo)準(zhǔn)在測試墊片參數(shù)時(shí),均假設(shè)施加在墊片上的應(yīng)力是均勻分布的。

然而,在實(shí)際的生產(chǎn)工作中,種種因素的影響會(huì)導(dǎo)致法蘭發(fā)生偏轉(zhuǎn),通過螺栓施加在墊片表面上沿徑向分布的接觸應(yīng)力是不均勻的。針對(duì)這一現(xiàn)象,現(xiàn)有文獻(xiàn)中普遍采用有限元法(FEM)對(duì)墊片的接觸應(yīng)力進(jìn)行數(shù)值分析。

王璐等人[9]運(yùn)用ABAQUS分析了當(dāng)各螺栓施加的預(yù)緊力產(chǎn)生差異時(shí),墊片接觸應(yīng)力的分布情況。盧志珍、朱樂等人[10-11]運(yùn)用ANSYS自帶的襯墊單元模型Gasket,向墊片施加位移載荷,且步長為2 s,從而得出墊片的壓縮回彈性曲線,借此分析其密封性能。喻健良等人[12]運(yùn)用ABAQUS,分析了不同加載方式和墊片型式對(duì)螺栓交互作用的影響。OMIYA Y等人[13-14]運(yùn)用ABAQUS,分析了在各螺栓預(yù)緊力相同的情況下,墊片的接觸應(yīng)力分布情況,并通過實(shí)驗(yàn)對(duì)此進(jìn)行了驗(yàn)證。

有限元法是目前一種主流的數(shù)值分析方法,并已經(jīng)得到了廣泛的應(yīng)用。但在計(jì)算薄壁結(jié)構(gòu)、應(yīng)力集中、無限域等問題時(shí),其計(jì)算精度及計(jì)算效率較低。為彌補(bǔ)有限元法的不足,近年來諸如無網(wǎng)格法[15]、邊界元法[16-19]等數(shù)值分析方法取得了長足進(jìn)步,各個(gè)瓶頸問題也相繼得到了解決。

邊界元法(BEM)是在邊界積分方程理論基礎(chǔ)上建立起來的一種純邊界離散型數(shù)值分析方法。相較于其他數(shù)值分析方法,其具有離散單元數(shù)量較少、數(shù)據(jù)準(zhǔn)備簡單、計(jì)算量小的優(yōu)勢。但利用BEM分析墊片等薄型結(jié)構(gòu)的彈性力學(xué)問題時(shí),求解的大量近奇異積分會(huì)出現(xiàn)近奇異性,且被積函數(shù)會(huì)隨距離的減小而急劇變化,需要大量高斯積分點(diǎn)才能獲得較好的計(jì)算精度。這一情況嚴(yán)重影響了該方法的計(jì)算效率。

針對(duì)薄型結(jié)構(gòu)分析中的積分近奇異性消除問題,SLADEK V等人[20]于1993年提出了正則化法。2014年,ZHANG Xi-yu等人[21]也提出了一種基于薄型結(jié)構(gòu)混合邊界節(jié)點(diǎn)法的理論分析方法,數(shù)值算例表明了該方法具有一定的適用性。2019年,張見明等人[22]提出了一種新的單元細(xì)分法(基于體二叉樹),大幅提高了奇異和近奇異積分的計(jì)算穩(wěn)定性及精度。

在不同的方法中,非線性變換法能更好地利用計(jì)算機(jī)軟件,對(duì)其進(jìn)行模塊化編程,并且可以不依賴積分核函數(shù);但其計(jì)算精度和穩(wěn)定性受到積分域內(nèi)部投影點(diǎn)位置的影響。

筆者將針對(duì)弱化投影點(diǎn)影響力的新型非線性變換法進(jìn)行研究,提出一種非線性組合式sinh-Sigmoidal變換方法,并將其集成到邊界元程序,以消除積分在徑向和角度方向的近奇異性;然后,分別在理想工況和實(shí)際工況下,采用BEM和FEM程序分析薄型墊片的彈性靜力學(xué)特性,以驗(yàn)證該方法的有效性。

1 邊界元法

筆者以彈性力學(xué)問題為例進(jìn)行說明,將邊界元法應(yīng)用于實(shí)際力學(xué)問題的求解。

經(jīng)典彈性力學(xué)問題的平衡方程和邊界條件描述如下[23]:

(1)

其中:對(duì)于三維問題,均采用指標(biāo)形式記法,下標(biāo)i,j=1,2,3表示對(duì)其所代表的變量求偏導(dǎo)數(shù),即σij,j=?σij/?xj。

同一變量中,若下標(biāo)重復(fù)出現(xiàn)即表示求和,其幾何方程和物理方程如下:

(2)

式中:δij為Kronecker符號(hào),當(dāng)下標(biāo)i=j時(shí)通常取值為1,否則為零;λ,μ均為Lame彈性常數(shù)。

λ,μ與彈性模量E、泊松比ν以及剪切模量G之間的關(guān)系如下:

(3)

經(jīng)典彈性力學(xué)問題相應(yīng)的邊界積分方程常表示如下:

(4)

對(duì)于三維各向同性體,其基本解為開爾文(Kelvin)解。位移和面力的基本解表示如下[24]:

(5)

(6)

式中:r(x,y)為源點(diǎn)y與場點(diǎn)x間的歐幾里得距離。

其中:位移的基本解滿足愛因斯坦求和約定,當(dāng)l=i時(shí),δli=1,其余情況取值均為零。

假設(shè)源點(diǎn)y位于光滑的積分邊界上,則取系數(shù)clj(y)=1/2。在不考慮體力影響的情況下,可得只包含邊界積分項(xiàng)的積分方程,通過單元插值法將所求解的具體問題的邊界進(jìn)行離散化處理。

對(duì)位移和面力進(jìn)行等參差值計(jì)算如下:

(7)

(8)

式中:m為邊界離散的單元總數(shù)量;Nk(ξ,η)則為離散單元內(nèi)部第k個(gè)插值點(diǎn)所對(duì)應(yīng)的形函數(shù)。

筆者通過廣義達(dá)菲變換,將坐標(biāo)轉(zhuǎn)換至(ξ,η)空間,得到了正則化的參數(shù)坐標(biāo)。在給定的相應(yīng)邊界條件下,將場點(diǎn)x取遍積分單元內(nèi)所有插值點(diǎn)的位置,可得3N×3N規(guī)模的線性方程組(其中,N為總的插值點(diǎn)數(shù)量)。

通過計(jì)算機(jī)編程求解,筆者可得邊界上任意未知的位移或面力值。而彈性體內(nèi)任意一點(diǎn)的位移、應(yīng)力、應(yīng)變的值則可以根據(jù)式(4)計(jì)算得出。

2 sinh-sigmoidal組合式變換法

筆者利用BEM分析薄型結(jié)構(gòu)的彈性力學(xué)問題,求解大量的近奇異積分,公式如下:

(9)

式中:f為不存在近奇異性的光滑函數(shù);x為域內(nèi)被積點(diǎn);y為域外源點(diǎn);r為兩點(diǎn)間的距離。

當(dāng)分母rl趨近于零時(shí),積分在徑向和角度方向均會(huì)出現(xiàn)近奇異性,被積函數(shù)隨距離的減小而急劇變化,需要大量高斯積分點(diǎn)才能獲得較好的計(jì)算精度,但其嚴(yán)重影響了計(jì)算效率。

因此,精確高效地求解近奇異積分是利用BEM分析薄型結(jié)構(gòu)問題的關(guān)鍵。基于自適應(yīng)分塊技術(shù)和不同坐標(biāo)變換,筆者提出一種非線性sinh-sigmoidal組合變換法,將其與原始極坐標(biāo)變換下(ρ,θ)坐標(biāo)空間中的近奇異積分相結(jié)合,可以在提高積分計(jì)算精度的同時(shí)大幅降低計(jì)算量,彌補(bǔ)傳統(tǒng)變換法的不足。

2.1 原始極坐標(biāo)變換

局部坐標(biāo)系中的距離函數(shù)如圖1所示。

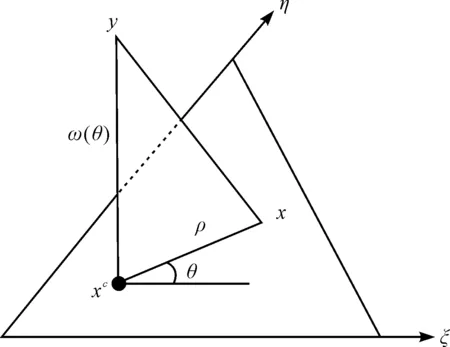
圖1 局部坐標(biāo)系中的距離函數(shù)

在三角形單元中,距離源點(diǎn)y最近的點(diǎn)為投影點(diǎn)xc,兩者的連線垂直于積分單元中xc處的切線。

根據(jù)源點(diǎn)y的位置,即可確定投影點(diǎn)xc的位置。在投影點(diǎn)附近使用泰勒公式展開如下[25-26]:

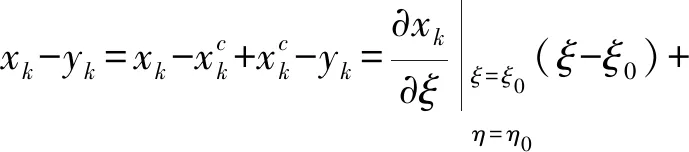
(10)

式中:(ξ0,η0)為投影點(diǎn)在局部空間坐標(biāo)系(ξ,η)內(nèi)的參數(shù)坐標(biāo)。

以(ξ0,η0)為極坐標(biāo)原點(diǎn)變換所得,則ξ、η的表達(dá)式如下:

(11)

將式(11)代入式(10)可得:

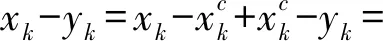
(12)

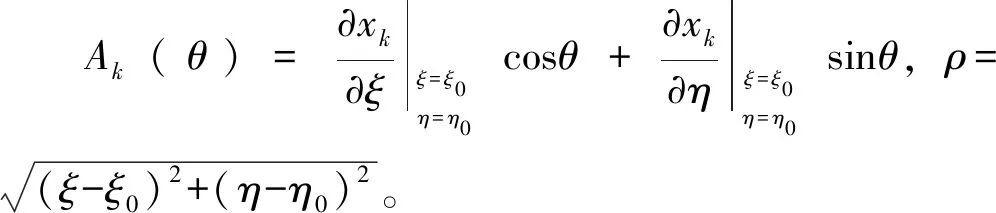
從源點(diǎn)y到場點(diǎn)x的實(shí)際距離r又可以表達(dá)如下:

(13)

其中:ω(θ)=r0/A(θ),A(θ)=|Ak(θ)|。

在局部坐標(biāo)空間系(ξ,η)中,筆者對(duì)近奇異積分的一般形式即式(9)進(jìn)行原始極坐標(biāo)變換,其表達(dá)式如下:

(14)

由式(14)可得,原始極坐標(biāo)變換將積分空間從(ξ,η)轉(zhuǎn)換至(ρ,θ),且徑向和角度方向上均出現(xiàn)了積分近奇異性。

2.2 徑向變換

為保證投影點(diǎn)位于積分形狀良好的子三角形單元內(nèi)部,降低積分形狀對(duì)計(jì)算精度的影響。筆者對(duì)每個(gè)積分單元運(yùn)用自適應(yīng)分塊技術(shù),將sinh變換重新定義如下:

r(s)=ω(θ)sinh(μ1s-η1)

(15)

將積分區(qū)間[0,ρ(θ)]和[θm,θm+1]分別轉(zhuǎn)換至區(qū)間[-1,1],可得:

(16)

因?yàn)橥队包c(diǎn)位于積分單元邊界的高階近奇異積分精度不夠,所以迭代sinh變換是必要的。其公式如下:

s(u)=a+bsinh(μ2u-η2)

(17)

其中:a=-1,b=π/2μ1。將引入的新變量的積分區(qū)間轉(zhuǎn)換至具體區(qū)間[-1,1],簡化編程過程,可得下式:

(18)

將式(15)和式(17)代入式(14),可得:

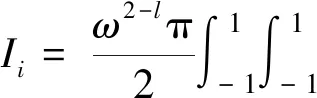
(19)

筆者將上述積分區(qū)間從未知量轉(zhuǎn)換成已知量,可消除積分核函數(shù)在徑向上的積分近奇異性;但角度方向的積分近奇異性依然存在。

2.3 角度方向近奇異性

在典型的sigmoidal變換中,其核函數(shù)能有效地向積分區(qū)間兩端大量聚集高斯積分點(diǎn)。利用這個(gè)特點(diǎn),可將其應(yīng)用于消除角度方向積分近奇異性。常用變換式如下:

(20)

式中:w為變換變量的冪指數(shù),且w≥1。

由此又可得到:

(21)

為了消除積分的雙向近奇異性,并提升計(jì)算的精度,將式(21)代入式(19),可得:

(22)

在上述轉(zhuǎn)換過程中,通常取w=2,以獲得滿意的精度。

3 薄型墊片彈性靜力學(xué)特性分析

3.1 理想工況邊界元分析

根據(jù)上下表面及內(nèi)外環(huán)設(shè)定的邊界條件,以及無體力項(xiàng)的彈性力學(xué)邊界積分方程,筆者對(duì)墊片所有邊界節(jié)點(diǎn)處面力的變化情況進(jìn)行多方向分析,并通過不斷加大網(wǎng)格劃分密度和增加計(jì)算節(jié)點(diǎn)數(shù)量,以此來驗(yàn)證邊界元法的收斂性。

筆者對(duì)該薄型墊片的各個(gè)面施加x、y、z方向的位移邊界約束條件,如下:

(23)

為了驗(yàn)證邊界元法計(jì)算所得結(jié)果的收斂性,筆者取4種不同的網(wǎng)格尺寸以及單元、節(jié)點(diǎn)數(shù)量,對(duì)薄型墊片所有邊界計(jì)算節(jié)點(diǎn)進(jìn)行x、y、z方向上面力變化情況的誤差分析。

邊界節(jié)點(diǎn)各方向面力的平均誤差計(jì)算結(jié)果如表1所示。

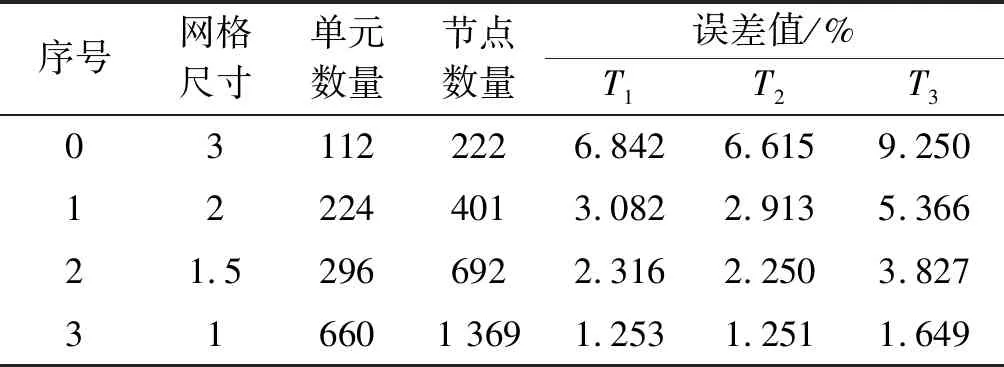
表1 邊界節(jié)點(diǎn)各方向面力的平均誤差計(jì)算

邊界節(jié)點(diǎn)各方向面力的平均誤差值分析結(jié)果如圖2所示。

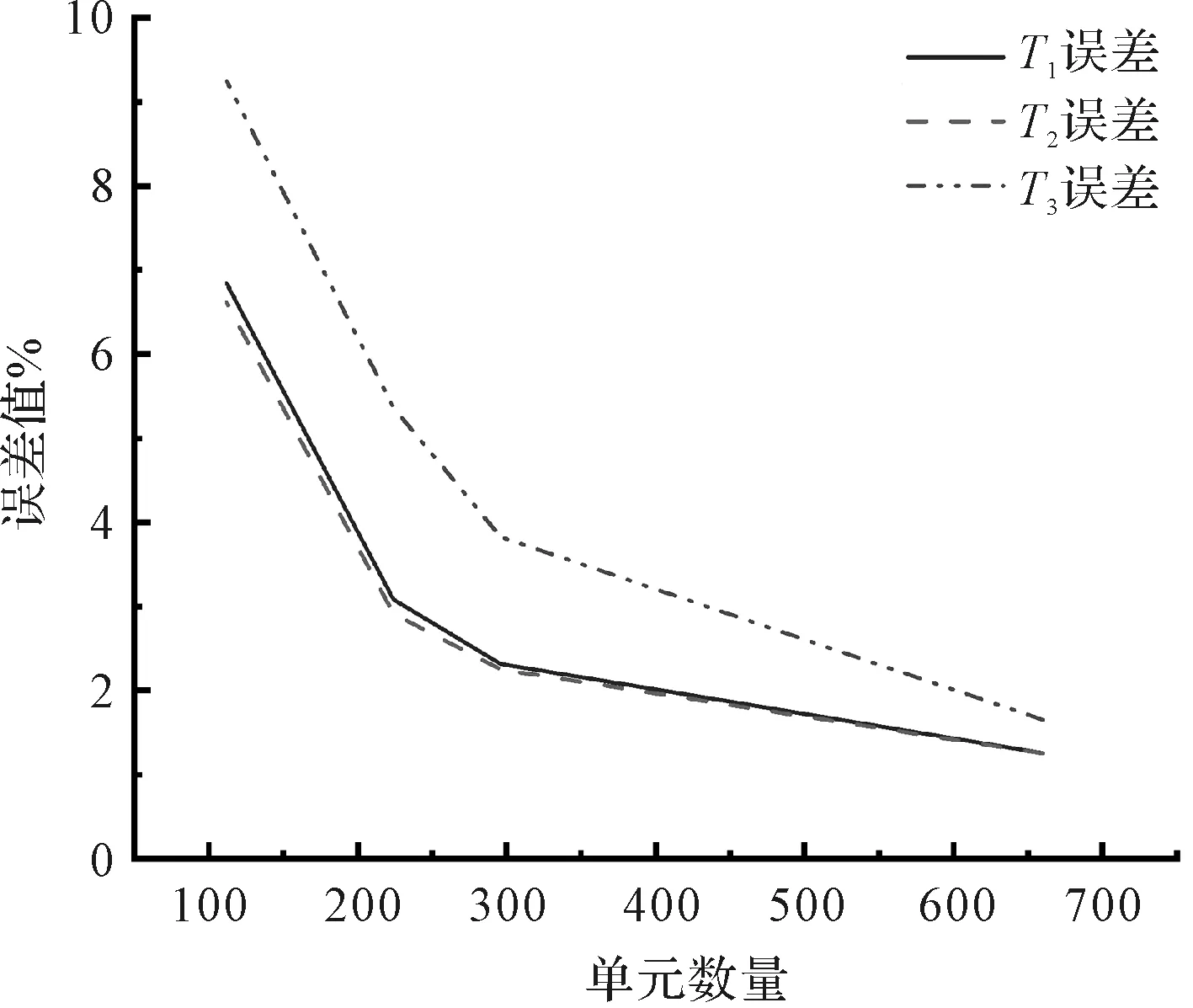
圖2 邊界節(jié)點(diǎn)各方向面力的平均誤差值分析

圖2中結(jié)果顯示:隨著網(wǎng)格尺寸的不斷細(xì)分,單元和節(jié)點(diǎn)數(shù)量的不斷增加,計(jì)算節(jié)點(diǎn)處的誤差值不斷減小。

運(yùn)用BEM程序計(jì)算可得,x、y、z方向上節(jié)點(diǎn)位移的數(shù)值結(jié)果能有效地收斂到精確解,說明該方法在分析薄壁結(jié)構(gòu)彈性力學(xué)問題時(shí)是精確可行的。

3.2 實(shí)際工況墊片受力變形分析

上述結(jié)果已經(jīng)驗(yàn)證了邊界元法在理想工況下(在各方向邊界條件均可以用公式描述),分析薄型墊片所得結(jié)果的有效性與正確性。

為進(jìn)一步驗(yàn)證該方法在實(shí)際工況下同樣具有可行性與一定的精度,筆者分別采用兩種方法(BEM、FEM)分析計(jì)算墊片受外力影響下的變形情況。

薄型墊片的約束條件及載荷施加如圖3所示。

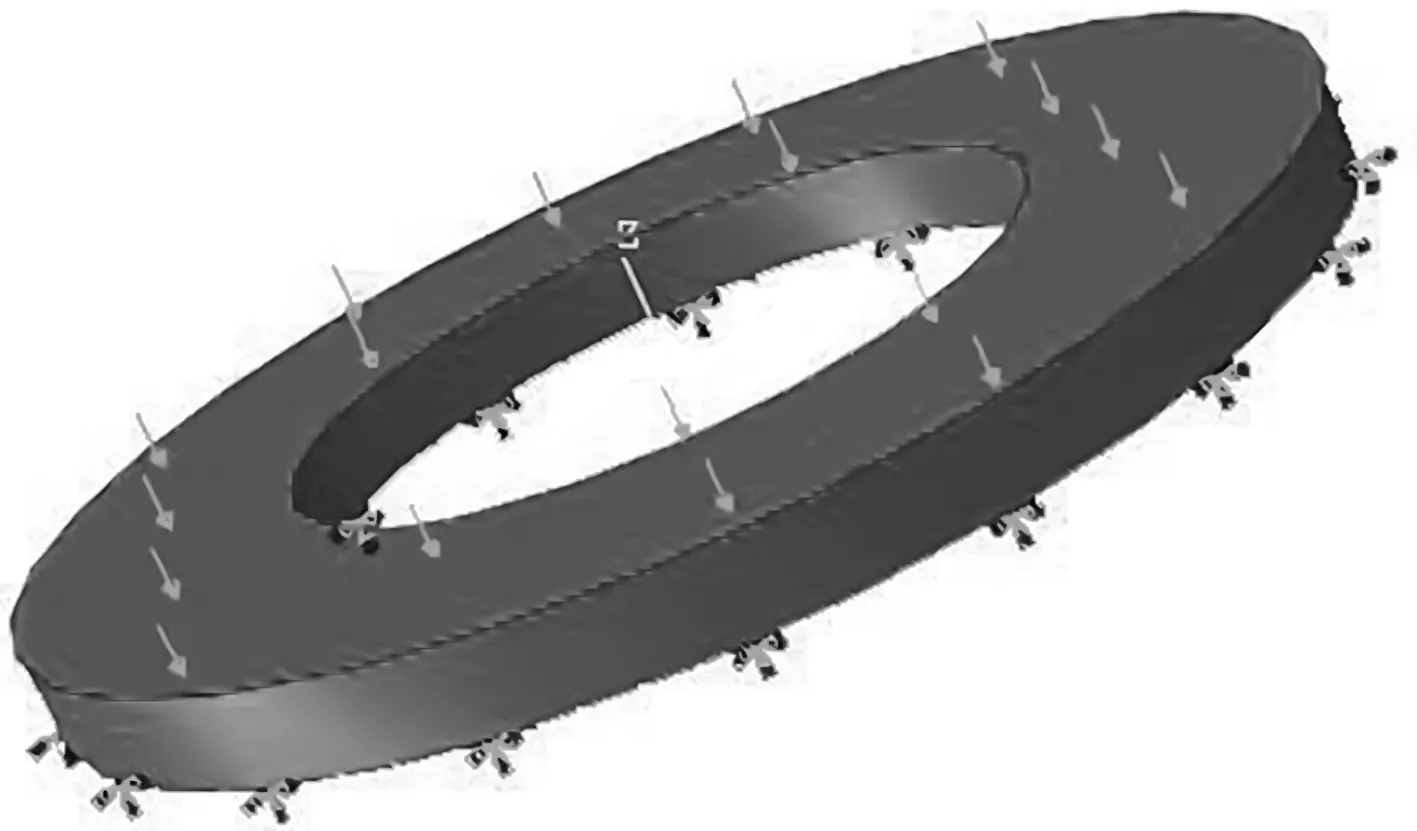
圖3 墊片模型受力情況

因薄型墊片的結(jié)構(gòu)輕量化,此處不考慮自重產(chǎn)生的變形。筆者將其一端面固定,另一端面施加壓力。

邊界元法程序網(wǎng)格劃分如圖4所示。

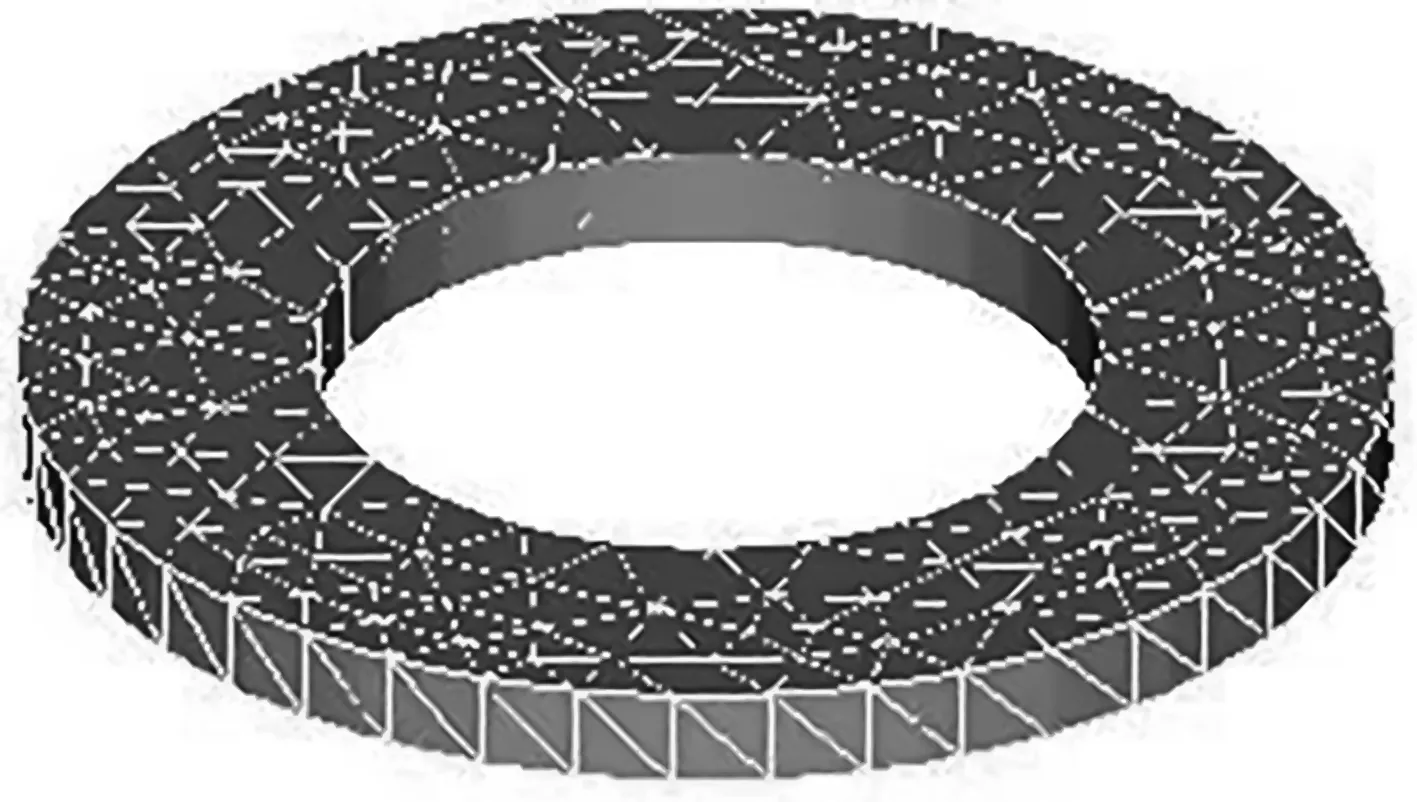
圖4 邊界元法網(wǎng)格劃分

為了獲得更為精確的變形結(jié)果,筆者在邊界元法分析中使用了1 296個(gè)三角形單元,域內(nèi)及表面共計(jì)使用2 113個(gè)節(jié)點(diǎn)。

筆者采用ABAQUS有限元軟件對(duì)墊片模型進(jìn)行網(wǎng)格劃分,其結(jié)果如圖5所示。

圖5 有限元法網(wǎng)格劃分

在有限元法分析中,筆者共計(jì)使用了126 350個(gè)線性六面體單元(C3D8R)以及142 791個(gè)節(jié)點(diǎn)。

采用ABAQUS有限元軟件對(duì)模型進(jìn)行分析,可以得到z方向的位移變形云圖,如圖6所示。

圖6 基于有限元法的z方向位移云圖

墊片在z方向位移變形范圍區(qū)間為[-2.069,0]。

為進(jìn)一步驗(yàn)證邊界元法分析的精確性和高效性,筆者在其厚度方向均勻選取10個(gè)取樣點(diǎn),并進(jìn)行對(duì)比分析。

樣點(diǎn)坐標(biāo)及計(jì)算結(jié)果對(duì)比數(shù)據(jù)如表2所示。

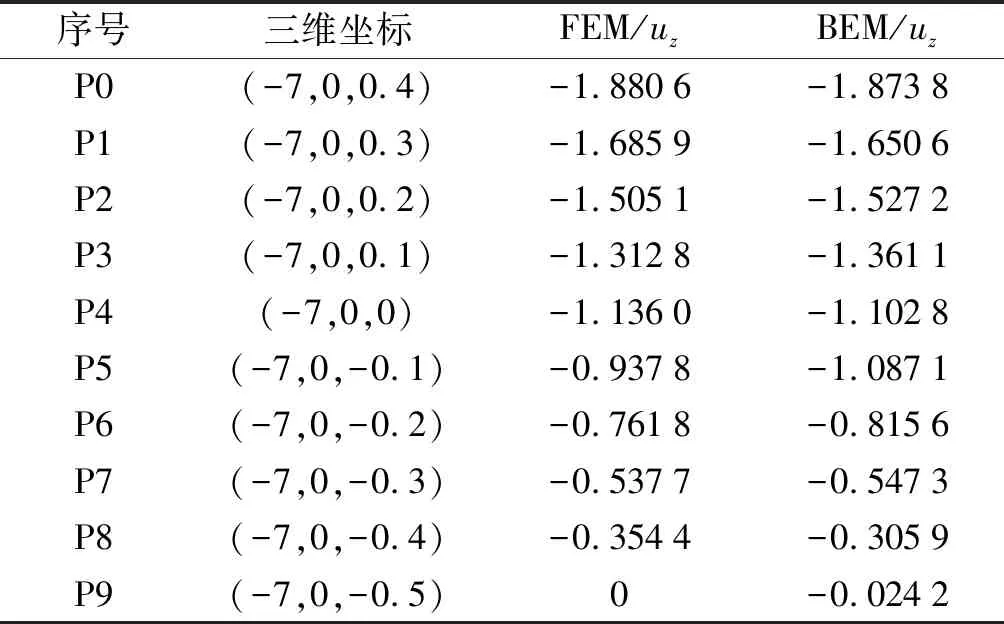
表2 樣點(diǎn)坐標(biāo)及2種方法計(jì)算結(jié)果對(duì)比

由表2數(shù)據(jù)可知:采用邊界元法,以極少的單元和節(jié)點(diǎn)數(shù)量計(jì)算所得z方向位移的變形結(jié)果,與采用有限元法分析所得到的結(jié)果相近。

厚度方向FEM與BEM的位移計(jì)算結(jié)果對(duì)比如圖7所示。

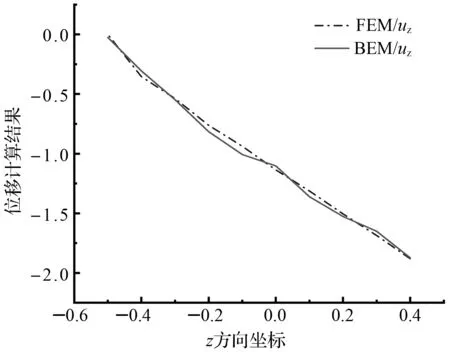
圖7 厚度方向FEM與BEM的位移計(jì)算結(jié)果對(duì)比

由圖7可知:運(yùn)用BEM程序計(jì)算得到的樣點(diǎn)處z方向位移線性圖,與ABAQUS軟件計(jì)算所得圖形趨勢基本吻合,并且從10個(gè)取樣點(diǎn)的具體數(shù)據(jù)值而言,上述2種方法間的計(jì)算誤差均小于1%。

由此可見,該算例也充分驗(yàn)證了邊界元法在實(shí)際工況下分析薄型墊片彈性力學(xué)問題的高效性以及精確性。

4 結(jié)束語

針對(duì)薄型結(jié)構(gòu)邊界元數(shù)值分析過程中的近奇異積分計(jì)算困難問題,筆者提出了一種基于sinh-Sigmoidal組合變換的解決方案,消除了積分在徑向和角度方向的近奇異性,并提高了邊界元法的計(jì)算效率和計(jì)算精度。

通過將其與有限元分析方法(FEM)進(jìn)行比較,結(jié)果驗(yàn)證了該方法的有效性,其是一種適用于薄型墊片彈性靜力學(xué)問題的有效數(shù)值分析方法。

研究結(jié)論如下:

1)采用迭代sinh變換可消除積分的徑向奇異性,采用Sigmoidal變換可消除角度方向奇異性;

2)通過理想工況下的薄型墊片算例分析,驗(yàn)證了BEM在計(jì)算墊片結(jié)構(gòu)面力時(shí)的收斂性和正確性;

3)通過實(shí)際工況下的薄型算例分析,對(duì)比了10個(gè)取樣點(diǎn)處BEM和FEM的位移計(jì)算結(jié)果,計(jì)算誤差均小于1%;但BEM方法的計(jì)算效率優(yōu)勢明顯,驗(yàn)證了BEM計(jì)算的高效性以及精確性;

4)在薄型墊片的設(shè)計(jì)中,可利用BEM對(duì)墊片進(jìn)行彈性力學(xué)分析,得到在表面預(yù)緊力作用下的變形曲線,再進(jìn)行相應(yīng)的補(bǔ)償設(shè)計(jì),以保證薄型墊片的連接可靠性,提高其密封性能。

當(dāng)前的研究主要考慮的是投影點(diǎn)位于積分單元內(nèi)部的情況。對(duì)投影點(diǎn)位于外部的情況,有待筆者進(jìn)一步深入研究。同時(shí),由于在當(dāng)前研究中,所分析對(duì)象為結(jié)構(gòu)簡單的圓形薄墊片,要使BEM方法能得到廣泛的應(yīng)用,未來還需針對(duì)更復(fù)雜的結(jié)構(gòu)開展研究。