齒輪傳動系統可靠性快速建模的數字化分析方法*

2023-10-26 13:27:22韓瑩瑩艾紅旭李梓源

機電工程 2023年10期

韓瑩瑩,艾紅旭,申強,李梓源,李威*

(1.中國船舶集團有限公司第七〇三研究所,黑龍江哈爾濱 150078;2.北京科技大學機械工程學院,北京 100083)

0 引言

機械系統的可靠性研究主要包括可靠性設計、分配、建模、分析、評價和改進等方面的內容。只有創建正確合理的模型,采用正確的分析方法,才能得到準確的可靠性評價結果,進而找出系統的薄弱環節,為系統可靠性設計提供依據,并制定相應的改進措施。

PFEUFER T[1]利用模型算法,對汽車的執行器進行了可靠性分析,在冗余方案的擴展中,基于模型算法的故障診斷方法有利于早期故障信號的檢測;但是,其未對參數化建模進行探究。何曉聰等人[2]研究了威布爾分布在齒輪減速器中應用,應用威布爾分布理論,導出了二級直齒圓柱齒輪減速器的一種壽命可靠性模型;但是,在模型中該研究只考慮了齒輪和軸承的可靠性,沒有考慮軸的可靠性。王正等人[3]綜合運用應力-強度干涉模型、順序統計量理論、泊松隨機過程以及概率微分方程,建立了零件的動態可靠性模型;但是,其未研究系統的可靠性建模方法。SADOU N等人[4]利用Petri網對動態系統進行了可靠性分析,提出了一種在Petri網中預測可能出現故障情況的方法;但對于復雜的系統,該方法會導致狀態空間爆炸。ZHANG G等人[5]建立了kriging可靠性模型,簡化了應力強度干涉模型的計算,并對大型球磨機齒輪傳動系統進行了可靠性計算;但是,在模型中其只考慮了齒輪的可靠性,沒有考慮軸承的可靠性。李春玲等人[6]依據零部件相關壽命,對風電齒輪箱太陽輪進行了可靠性建模;但是,其未對行星輪進行可靠性建模。孫道明等人[7]在考慮了失效模式相關性的條件下,對齒輪進行了可靠性建模,采用Monte Carlo仿真方法,得到了齒輪在兩種失效模式下極限狀態函數的散點圖;但是,其對于齒輪傳動系統可靠性的研究多落腳于單一零件故障模式下的可靠性模型,缺乏對考慮各個零件載荷相關性的齒輪傳動系統整體進行可靠性建模。

RASHID H S J等人[8]利用影響圖,對直升機變速箱進行了可靠性建模,針對主齒輪箱(main gear box,MGB)油系統相關事故,建立了安全風險模型;但是,其僅給出了關系模型,沒有給出相應的數學模型。XIE L等人[9]基于時域級數,對齒輪箱進行了可靠性建模,并定義了時域級聯系統;但是,其未分析各級之間的相互耦合關系。王春華等人[10]以可靠性等為約束條件,選取體積、重合度和傳動效率作為目標函數,利用改進粒子群算法,對行星齒輪傳動進行了多目標可靠性優化設計;但是,在優化設計模型中,其只考慮了太陽輪和行星輪,沒有考慮齒圈。于格等人[11]基于可信度,建立了齒輪可靠性模型,給出了基于性能裕量確信的可靠度計算流程和算法;但是,其僅對單級齒輪傳動系統進行了研究,沒有對多級齒輪系統進行探究。李明凱等人[12]研究了基于參數不確定條件下的齒輪彎曲疲勞可靠性計算及靈敏度分析方法;但是,其只開展了高應力區的成組法試驗,沒有開展低應力區的升降法試驗。QIAN H等人[13]基于Kriging模型,在多種故障模式下,對旋轉矢量(rotation vector,RV)減速器進行了時變可靠性建模分析;但是,其僅考慮了齒輪接觸和彎曲疲勞失效,未考慮齒面膠合失效。王春光等人[14]以系統動力學、可靠性、穩健性和體積作為目標函數,建立了直齒輪箱的可靠性穩健優化設計模型;但其沒有對斜齒輪進行探究。裴幫等人[15]以疲勞實驗數據為基礎,對某地鐵齒輪可靠性進行了分析;但是,其未考慮齒輪共因失效的影響。

由于齒輪傳動系統在實際工程使用過程中變得越來越復雜,由此帶來建模計算量越來越大、效率越來越低,因此,急需開展齒輪傳動系統可靠性快速建模數字化研究,以及開展相應軟件的開發工作。

針對復雜機械系統可靠性建模計算量大和耗時長等問題,綜合應力-強度干涉模型和載荷相關性,筆者建立定軸輪系、行星輪系及混合輪系的可靠性模型,設計開發齒輪傳動系統可靠性數字化建模軟件,完成參數化建模與自動化分析;最后,以功率分支齒輪傳動系統為例,采用解析法和數字化軟件,對其進行可靠性建模與分析,對可靠性快速建模數字化分析平臺的有效性進行驗證。

1 基于載荷相關性的系統可靠性模型

齒輪傳動系統的可靠性計算可通過系統邏輯關系和數學關系來實現。該計算主要體現在可靠性框圖的繪制與可靠度大小的計算方面。為了滿足齒輪傳動系統及子系統的可靠性定量要求,必須建立可靠性關系模型與可靠性數學模型。

筆者將以機械零件的可靠性建模為基礎,分析不同類型和結構特點的機械傳動系統可靠性建模方法;以功率分支齒輪傳動系統為例,給出2種機械傳動裝置可靠性建模方法的適用范圍。

機械零部件的可靠度計算是基于應力-強度分布干涉模型,零件的強度S和工作應力σ均為服從概率統計分布曲線的隨機變量。

作為可靠性設計的基本原則,零部件的強度值要高于應力值。對于固定值而言,其可以從安全系數上得以體現;而對于離散化后的隨機變量,往往并不能簡單地用一個參數來表示。

在特定條件下,強度與應力兩概率密度函數曲線發生了交叉,陰影部分稱為干涉區。

基于應力分布和強度分布的干涉理論,可靠度作為強度大于應力的總概率之和,其表達式如下:

(1)

當應力為xσ時,強度S大于該應力值的概率表示如下:

(2)

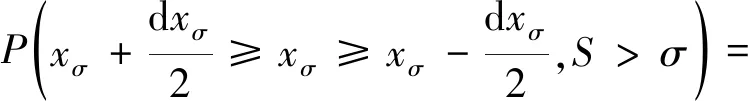
(3)

由此可知,在整個積分區間內,對應力σ進行積分,可得機械零部件的可靠度如下:

(4)

由于系統中不同零部件具有不同的功能,故各元素對系統的可靠性影響能力不同。通過分析對傳動系統影響較大的系統元素,即可近似得到真實的系統可靠性數值。

實際上,大多數機械傳動系統的可靠性模型應具有如下特征[16]:傳動系統任何一個零件失效將導致系統發生失效;同一傳動系統中,各零部件的失效既不會是獨立事件,也不會是完全相關事件,即存在一定程度的相關關系。

若機械傳動系統在廣義隨機載荷L的作用下運行,設載荷L的概率密度函數為fL(L),系統各零部件由此引起的應力Hi=Hi(L),fi(S)是第i個零件強度的概率密度函數,則在L=L0時,由式(4)可知零件的可靠度如下:

(5)

載荷L落在L0附近dL區間內的概率如下:

(6)

若各零件間關于強度Si是相互獨立的,則各零件均可靠的概率如下:

(7)

假設載荷L與各零件的強度相互獨立,對應于所有可能的L0,上述概率為系統的可靠度如下:

(8)

式(8)考慮了各零件關于載荷相關的系統可靠性干涉模型,根據式(7)及零件的可靠性干涉模型,系統可靠度計算公式如下:

(9)

由上述的推導可知,式(5)與式(9)在形式上存在明顯的區別。式(8)僅代表了一種系統可靠性計算模型,在處理復雜系統時,由于存在相當繁瑣的計算,故求解實際問題時并不常用。

2 基于可靠性建模的數字化軟件

齒輪傳動系統的可靠性建模是基于系統中各零部件間的故障邏輯關系,軟件運用系統可靠性框圖,表達系統的功能原理。筆者采用C#.NET,開發了一種基于普通概率法與蒙特卡洛模擬法的系統可靠性建模軟件。

可靠性建模數字化分析流程如圖1所示。

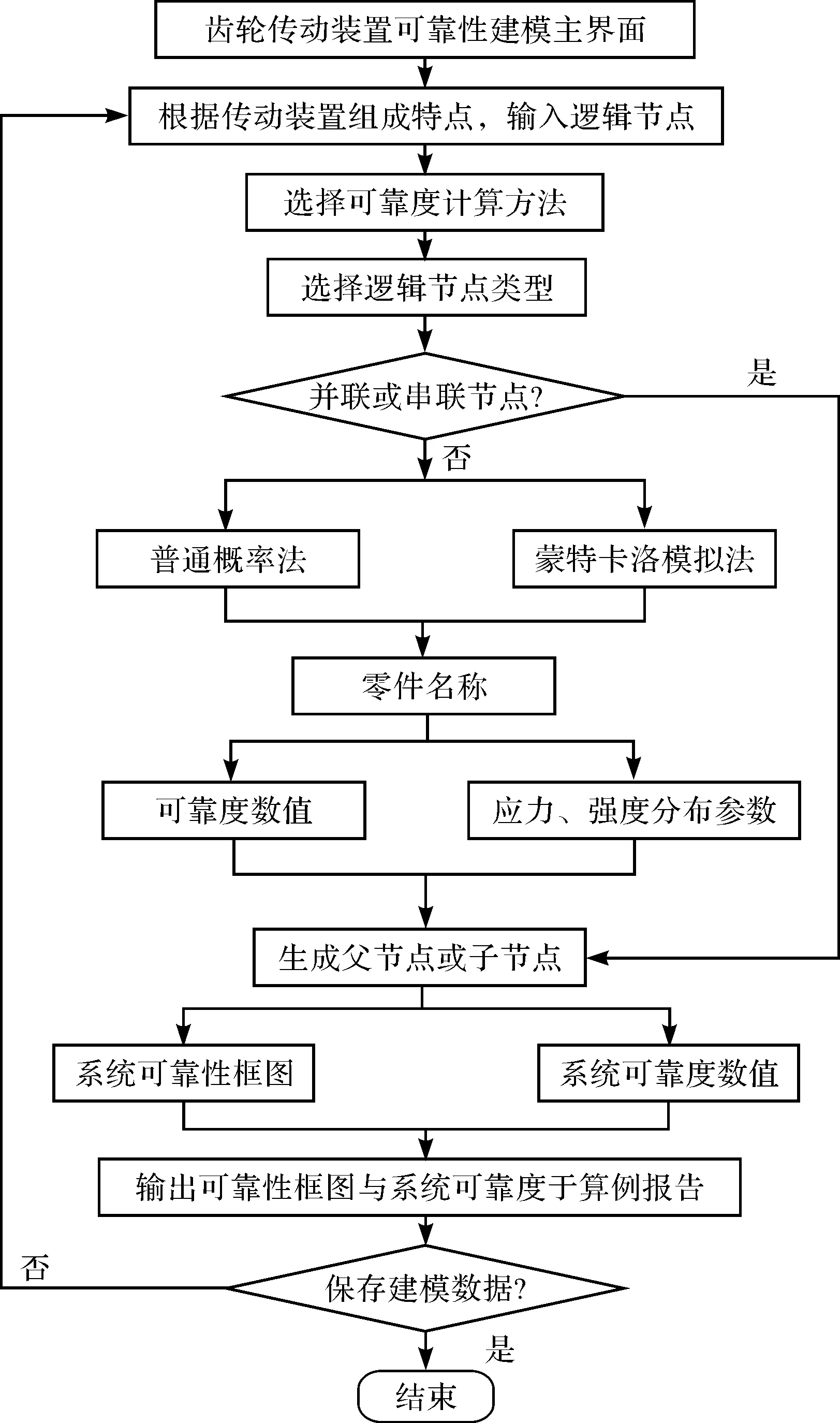
圖1 可靠性建模數字化分析流程

在完成機械零部件可靠性建模參數的輸入之后,結合樹形結構控件中節點間的邏輯關系,筆者最終繪制出系統的可靠性框圖。

可靠性關系模型輸出界面如圖2所示。

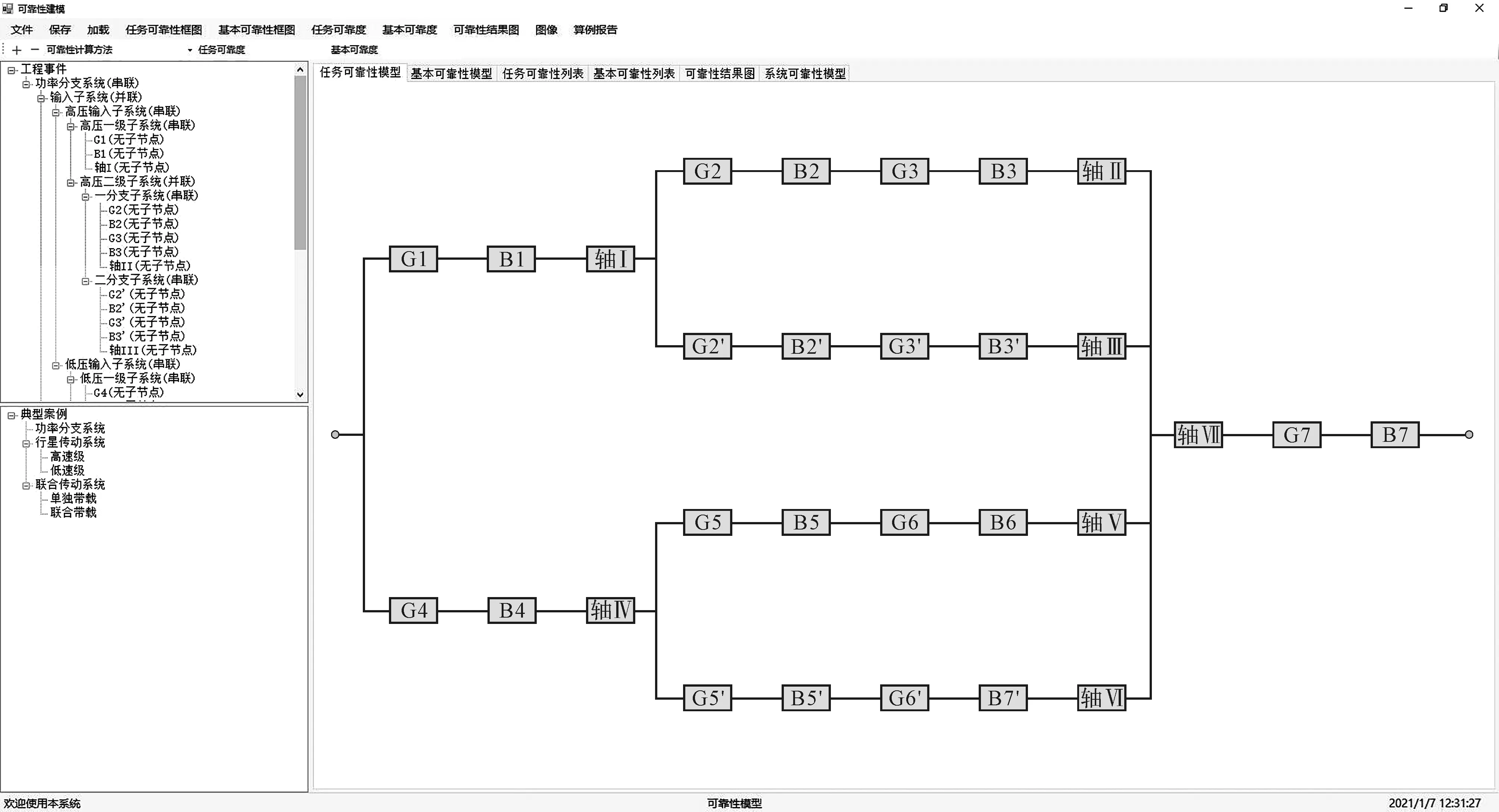
圖2 可靠性關系模型輸出界面

針對邏輯結構生成相應的基本可靠性框圖和任務可靠性框圖后,筆者設計通用算法,對用戶輸入的邏輯結構進行解析。

首先,需要判斷結構的基本可靠性模型和任務可靠性模型是否一致,判斷邏輯采用前序遍歷算法,其條件為結構中是否存在并聯關系節點。由于任務可靠性框圖不簡化混聯結構,邏輯算法的關鍵在于對混聯結構中并聯結構的處理,需要計算結構中最大串聯節點數。該函數對串聯結構返回各子節點最大串聯節點數之和,對并聯結構返回子節點最大串聯節點數。

設節點的最大串聯節點數為g。g算式如下:

(10)

式中:i為g的第i個子節點;k為g有k個子節點。

式(10)為遞歸公式。按照遞歸循環方法設計函數,即可得到輸入節點的最大串聯節點數。

為了表征任務可靠性框圖的邏輯信息,設第i個節點的位置信息為L。L算式如下:

Li=(xi,yi,wi)

(11)

式中:xi為第i個節點的橫坐標;yi為第i個節點的縱坐標;wi為第i個節點的所屬的縱向范圍。

邏輯信息的計算順序按照節點遍歷順序進行,該過程基于樹的前序遍歷。

其前序遍歷算法流程如圖3所示。

圖3 前序遍歷算法流程圖

遍歷全部節點的過程中,首先計算的初始值如下:

(12)

式中:Le為繪圖區域的長度,像素密度單位,PPI;W為繪圖區域的寬度,PPI;g0為根節點的最大串聯節點數。

當節點i為串聯節點,并且節點i+1為節點的第一個子節點時,L算式如下:

Li+1=Li

(13)

當節點i為并聯節點,并且節點i+1為節點的第一個子節點時,L算式如下:

(14)

當節點i為串聯節點,并且節點i+1為節點的領節點時,L算式如下:

Li+1=Li·E+(G,0,0)

(15)

當節點i為并聯節點,并且節點i+1為節點的領節點時,L算式如下:

(16)

當節點i為串聯節點,并且節點i+k為節點的領節點時,L算式如下:

Li+k=Li·E+(G·gi,0,0)

(17)

當節點i為并聯節點,并且節點i+k為節點的領節點時,L算式如下:

(18)

遍歷完畢全部零件節點后,筆者采用類以存儲各節點的邏輯位置信息,從而實現類對象與零件節點一一對應目的。由于基本可靠性框圖為全串聯模型,故只需生成每一零部件的可靠性框圖,依次排列后,即可完成該項建模任務。

然而傳動系統的任務可靠性框圖相對較復雜,需考慮串聯、并聯及混聯結構的空間布局與節點間的位置關系,因此,需針對串聯和并聯節點,分別基于遞歸思想,借助式(13)～式(18)得到其各子節點的坐標值。

3 算例及結果分析

以功率分支齒輪傳動系統為例,其功率分支齒輪傳動裝置結構如圖4所示。

圖4 功率分支齒輪傳動裝置結構圖

筆者根據該齒輪傳動系統的工作環境與所受載荷特點,建立其可靠性模型時只考慮齒輪、軸和軸承3類零件的影響。

由于零部件為單元串聯結構,故可以得到系統的基本可靠性框圖,如圖5所示。

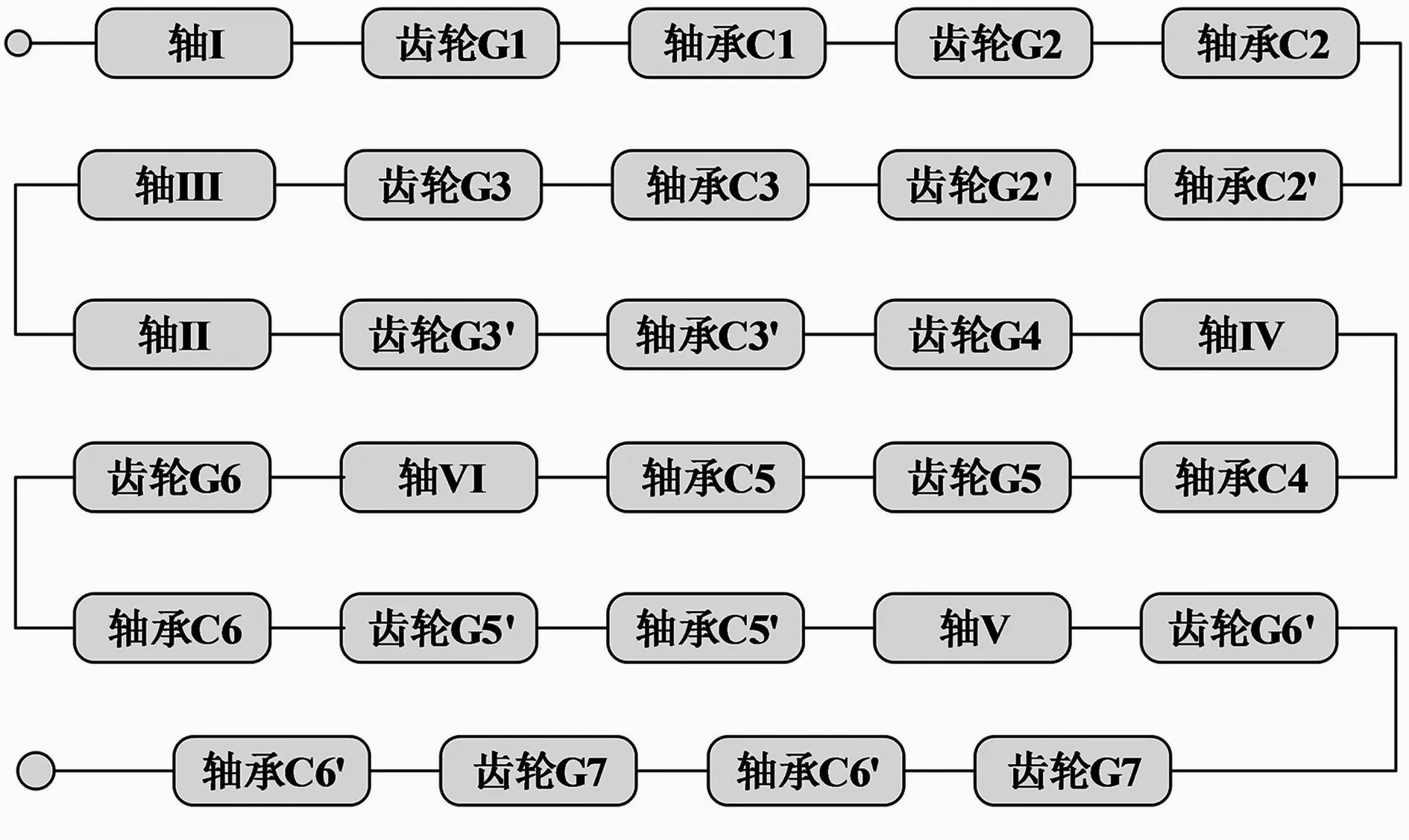
圖5 系統基本可靠性框圖

任務可靠性模型需根據傳動系統的工作特點,結合系統各零部件所執行的功能,得出包含串、并聯結構的任務可靠性框圖。

系統任務可靠性框圖如圖6所示。

圖6 系統任務可靠性框圖

筆者參照非電子元器件可靠性數據手冊(nonelectronic parts reliability data,NPRD)可靠性數據,得到各零部件的故障率,通過故障率與可靠度之間的轉化關系求得可靠度,最后將可靠度代入公式中,進行計算。

由理論推導可得,故障率λ與可靠度R(t)的計算關系如下:

(19)

如果組成系統的零部件數目較多,并且存在明顯的損耗性零件,對有限壽命已知的零件需要定期更換,則零件失效率λ可近似地認為是常數。

取工作時間為12 000 h,可得系統主要零部件失效率λ及可靠度如表1所示。

表1 統主要零部件失效率及可靠度

零件的可靠度可以采用蒙特卡洛模擬法得到。

蒙特卡洛模擬法模塊通常是利用MATLAB軟件,來模擬零件的可靠度計算過程。在進行模擬試驗之前,需要明確機械零部件強度與應力的概率分布情況,建立其應力-強度干涉模型,然后方能求解其可靠度。

同一工況下,齒輪應力與強度的蒙特卡洛擬合數據散點圖,如圖7所示。

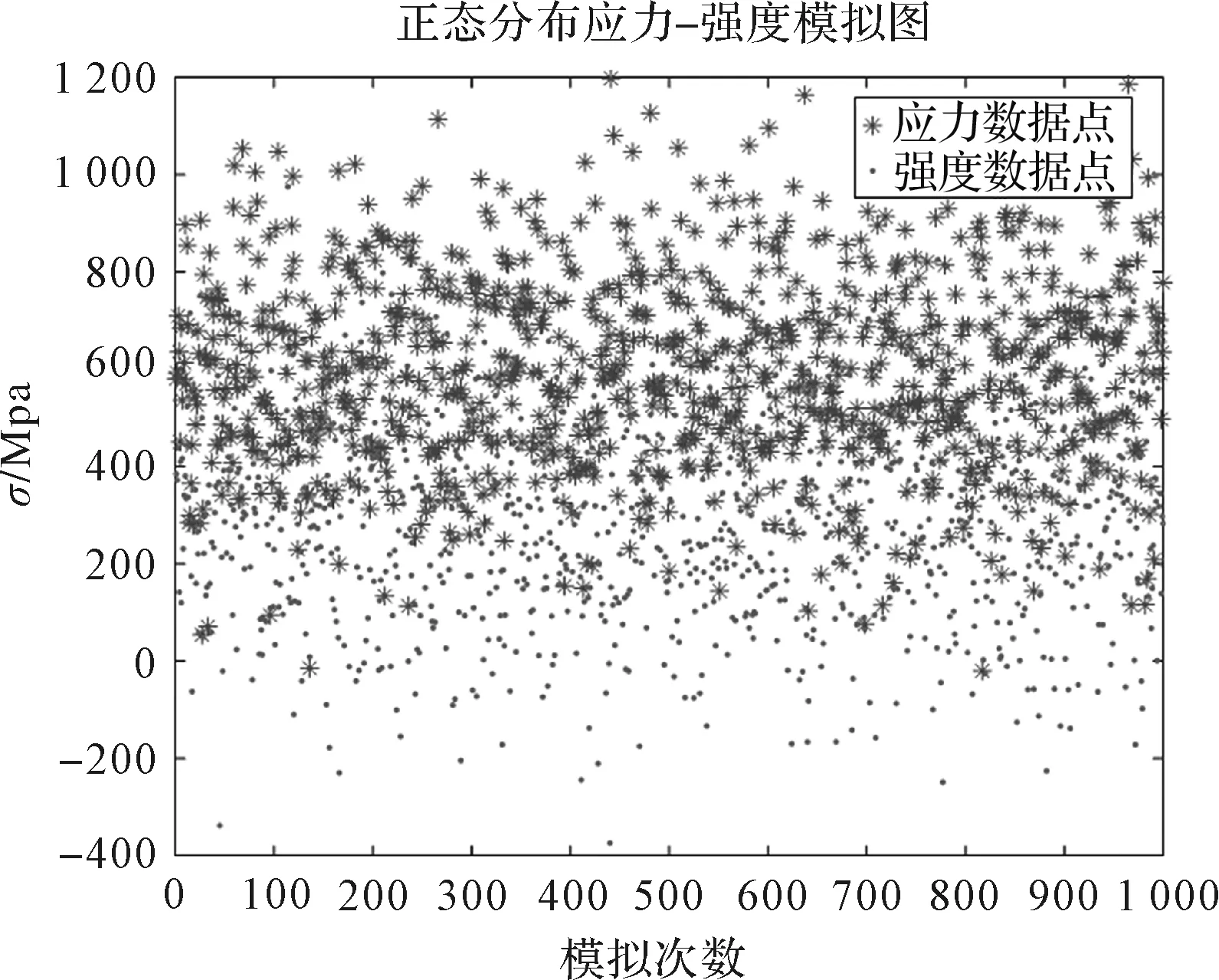
圖7 齒輪應力及強度的蒙特卡洛擬合數據散點圖

為了簡化其運算過程,可根據系統的任務可靠性框圖,將各分支路看成一個整體,而每一整體內部為串聯結構。

由串聯模型計算公式可得出各組成單元可靠度。

系統各單元可靠度如表2所示。

表2 系統各單元可靠度

由表2可得,該系統基本可靠性的可靠度:Rc=RA·RB·RC·RD·RE·RF·RG=0.834 4。

其中,設單元內部各零部件的可靠度為R1、R2。

最后,根據任務可靠性模型的計算特點,可得該系統的任務可靠度數值:Rb=RG·(RA·RH+RB·RI-RA·RB·RH·RI)=0.981 8。

因此,運用普通概率法,計算得到該功率四分支傳動系統的基本可靠度為0.834 4,任務可靠度為0.981 8。

齒輪傳動系統基本可靠度取決于各個環節的可靠度。若想提高系統的基本可靠度,需要采取有利于增加零部件自身可靠度的措施。

軟件生成基本可靠性與任務可靠性對比,如圖8所示(解析計算結果與軟件計算結果誤差為0.016%)。

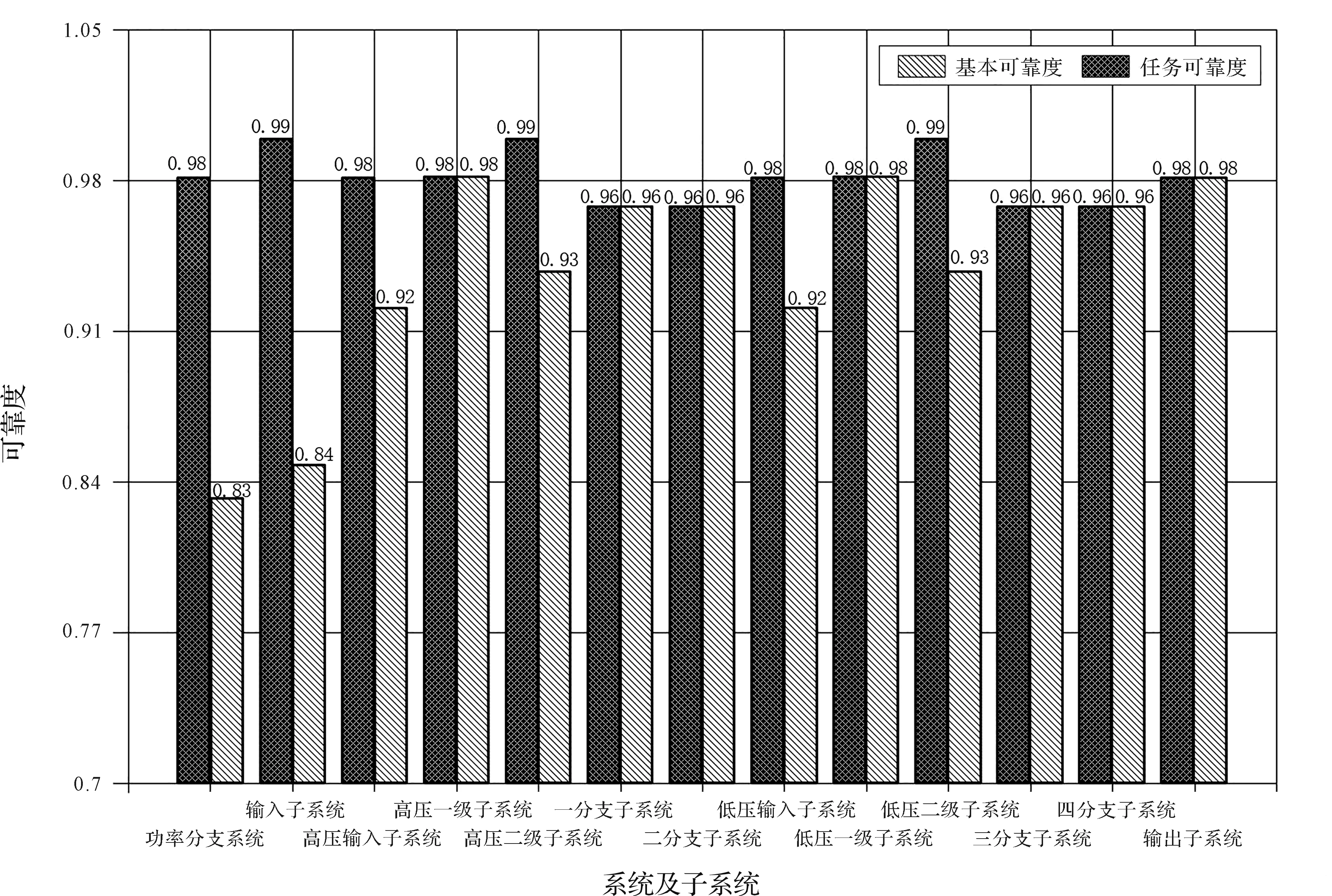
圖8 基本與任務可靠性結果對比圖

通過各子系統與系統的對比可得:隨著系統并聯部分的增多,基本可靠度與任務可靠性之間的差值會越來越大。因此,在可靠性設計中,可通過該圖快速判斷冗余系統的位置,為系統的合理設計提供支持。

為了驗證該可靠性數字化分析方法及軟件的正確性,筆者同時采用解析法進行了計算,兩者取得了較好的一致性。

4 結束語

針對復雜機械系統可靠性建模計算量大和耗時長等問題,綜合應力-強度干涉模型和載荷相關性,筆者提出了一種齒輪傳動系統可靠性快速建模的數字化分析方法,建立了考慮各個零件載荷相關性的系統可靠性模型,設計了齒輪傳動系統可靠性快速建模的數字化平臺;最后,以功率分支齒輪傳動系統為例,采用解析法和數字化軟件,對其進行可靠性建模與分析,對可靠性快速建模數字化分析平臺的有效性進行驗證。

研究結論如下:

1)筆者建立了基于零件載荷相關性的齒輪傳動系統可靠性模型,研究了齒輪傳動系統可靠性關系模型,推導了基本可靠性和任務可靠性數學模型,實現了根據實際齒輪傳動結構選用混聯模型表征可靠性關系模型的目的;采用數理統計概率法,對可靠性數學模型進行了求解,得到了系統基本可靠度為0.834 4,任務可靠度為0.981 8,提高了系統可靠性建模精度;

2)開發了齒輪傳動系統數字化分析平臺可靠性建模模塊,在前處理部分實現了輸入模型結構參數;在中間處理部分根據邏輯結構和遞歸思想,采用遍歷模型,計算了可靠性模型框圖參數,采用蒙特卡洛法計算了可靠度;在后處理模塊實現了自動生成基本可靠性及任務可靠性模型框圖、系統可靠性結果表格、可靠性結果對比圖和自動輸出可靠性建模分析報告Word文檔目標,提高了系統可靠性建模效率;

3)基于所開發的齒輪傳動系統數字化分析軟件可靠性建模模塊,對功率分支齒輪傳動系統進行了可靠性建模數字化分析,軟件仿真分析結果與解析計算結果取得了較好的一致性,驗證了筆者所提出的可靠性建模數字化分析方法(及軟件)的可行性和正確性。