帶功能梯度過渡區域的各向異性轉動圓環的彈性分析*

彭旭龍, 謝小朋, 黃海平, 魏文超, 唐雪松

(1. 長沙理工大學 土木工程學院 力學系, 長沙 410114;2. 中車株洲電力機車有限公司, 湖南 株洲 412000)

0 引 言

受輕量化和高性價比材料需求的驅動,復合材料在航空航天、交通運輸、生物工程、核能發電、航海與軍事等領域發揮著至關重要的作用[1-3]．然而,不同的材料黏結界面成分差異明顯,界面出現強度不匹配,導致材料發生大尺度的變形和高梯度的殘余應力從而使材料失效[4]．功能梯度材料(functionally graded materials,FGMs)因其力學性能隨著空間位置的變化而變化,所以可以解決這些問題．自然界中存在著很多具有功能梯度特性的材料,比如木材、動物的骨骼、貝殼等都是常見的天然功能梯度材料,且其截面都具有明顯的環形層狀結構[5]．這類結構因其良好的物理和力學特性,在機械和航空航天等工程應用中有著極其重要的作用,許多研究人員對其帶來的新的力學問題產生了濃厚的興趣．Dai等[6]求得了在離心力和熱荷載作用下功能梯度圓環的應力和應變場的半解析解．Danesh和Asghari[7]基于應變梯度理論分析了轉動圓盤的彈性力學行為．Obata和Noda[8]使用變分方法推導了功能梯度空心圓柱體和球體的控制方程和邊界條件,并求得了穩態熱應力的解析解．陳康等[9]假設盤心彈性模量分段梯度變化,提出了一種盤心局部梯度的輪盤結構,并采用等厚圓環法計算了輪盤的彈性應力場分布．Abdalla等[10]假定材料沿徑向呈冪函數梯度變化,利用有限元法分析了功能梯度轉動空心盤的熱應力行為．張瑩等[11]用England-Spencer板理論研究了材料梯度因子、板的厚度以及無量綱正應力對功能梯度圓板的影響．Horgan[12]研究了功能梯度各向同性線彈性材料受內壓作用空心圓柱體和旋轉圓盤的應力響應問題．Peng和Li[13-15]對任意梯度變化的各向同性受壓功能梯度空心圓筒和圓環等軸對稱結構進行了彈性和熱彈性分析．

從力學研究的角度看,功能梯度材料最突出的特點是其材料的非均勻性,這使得描述其力學問題的控制微分方程都是變系數的．因此,以往在處理功能梯度材料相關問題時,通常假設材料性能按某些特定函數變化,然后來求得相關問題的解析解[16-19]．然而,功能梯度材料性能的實際變化形式非常復雜,將材料性能簡單假設為坐標的特定函數很難符合實際情況．因此,近年來發展了一些新的數值計算方法．劉思敏等[19]發展了一種用于求解典型連續及不連續各向異性穩態熱傳導問題的數值流形方法．俞海和劉云鵬[20]研究了層狀梯度對Cu/WCP功能梯度材料力學性能的影響,并通過有限元方法模擬了5層Cu/WCP功能梯度材料在沿層向方向拉伸作用下的變形特性及力學行為．Omer[21]基于Pascal多項式和多尺度技術提出了一種求解各向異性功能梯度材料平面彈性方程的無網格方法,且通過邊界元等方法證明了該理論的準確性．彭旭龍等[22-23]采用積分方程方法,推導了轉動圓盤軸對稱平面應力問題中關于徑向應力的積分方程,并采用數值方法對該積分方程進行了求解．劉旭和姚林泉[24]通過Hamilton原理,得到了在溫度變化和由旋轉運動引起的面力作用下旋轉功能梯度納米環板的徑向和橫向耦合運動微分方程,并通過數值計算對該環板進行了振動分析．另一方面,從材料制備和材料性能來看,功能梯度材料更多地表現為各向異性．Bhattacharya等[25]設計、合成和表征了兩種沿軸向分布的多層功能梯度材料,并采用擴展有限元法分析了各向異性功能梯度材料在機械荷載作用下的疲勞問題．Yildirim[26]采用解析與數值的方法,通過施加可能的邊界條件和常用的材料分級規則(如簡單冪次和指數模式),對極正交各向異性功能梯度材料制成的圓盤進行了彈性分析．唐長亮等[27]考慮了各向異性功能梯度材料的飛輪,并建立了飛輪的力學方程,考察了橫向拉伸對應力和變形的影響．有關各向異性功能梯度夾層圓環結構相關力學問題的研究雖然取得了一些成果,但大都是針對材料性能呈特殊梯度變化的情況[28]．有關沿徑向任意梯度變化的夾層各向異性功能梯度圓環的研究還不多,如果能夠給出一種通用的方法得到夾層圓環材料關于任意梯度參數變化情況的解析解或近似解,無疑將會為功能梯度材料的設計和夾層圓環結構的優化提供重要的理論指導意義．

鑒于此,本文仿照生物學中貝殼的三層環狀結構,建立了具有3個不同區域的各向異性圓環,內層與外層為均勻各向異性材料,中間層為材料性能沿徑向任意變化的功能過渡區域．考慮其繞剛性軸勻速轉動,推導得到其控制方程,并給出一種有效的積分方程方法,將問題轉化為求解關于徑向應力的Fredholm積分方程,從而通過對積分方程的數值求解得到夾層圓環的應力和位移場的分布情況,并研究了材料不同的梯度參數變化對應力和位移場的影響．

1 模型建立問題描述

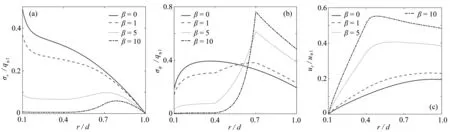
如圖1所示,仿照自然界中貝殼的三層環狀構造結構,考慮一個固結于剛性軸上的功能梯度夾層圓環,外部受均布壓力q0作用且以角速度ω繞剛性軸勻速轉動．該圓環由相互之間黏結非常好的3個區域組成,分別記為區域Ⅰ(a≤r

(1)

對于各向異性材料,Poisson比νrθ,νθr與徑向、環向彈性模量Er,Eθ之間存在以下關系:

(2)

假設圓環的軸向厚度很小,則本問題可以考慮為軸對稱的平面應力問題．因此結構內僅有徑向位移ur不為零,其幾何方程為

(3)

(4)

本構方程為

(5)

(6)

其中εr,εθ和σr,σθ分別表示結構內各點處的徑向、環向應變和徑向、環向應力．同時,應力分量應滿足如下平衡方程:

(7)

現假定夾層圓盤繞剛性軸以角速度ω勻速轉動且承受均布外壓q0作用,同時結構內部各區域之間黏結得非常好,則應滿足如下的邊界條件:

(8)

特別說明,與式(1)類似,本文用上標Ⅰ、Ⅱ、Ⅲ來區分各區域的物理量．

2 過渡層材料性能沿徑向呈冪函數梯度變化

以往關于功能梯度材料相關的力學研究中,為求得問題的解析解,通常將材料性能假設為空間坐標的某種特殊函數,比如冪函數和指數函數．因此,我們首先也假設過渡區域Ⅱ的材料性能沿徑向呈冪函數變化:

(9)

下面給出功能過渡區域Ⅱ的求解過程,對于均勻各向異性區域Ⅰ和Ⅲ可由相似過程簡單求出．在區域Ⅱ,將式(9)代入本構方程(5)和平衡方程(7)得

(10)

其中λ為材料的各向異性度,為環向彈性模量Eθ與徑向彈性模量Er的比值:

(11)

(12)

其中

系數A2,C2由邊界條件和連續性條件確定．因此,區域Ⅱ的應力分量可以表示為

(13)

(14)

區域Ⅰ和Ⅲ的位移分量和應力分量可類似求得．因此,夾層結構內的應力和位移場表達式可整體表示為

(15)

(16)

(17)

其中a≤r1≤b,b≤r2≤c,c≤r3≤d,

待定系數A1,A2,A3,C1,C2,C3可由邊界條件以及連續性條件(8)得到．建立矩陣方程X=P-1Q即可求得X=[A1A2A3C1C2C3]T的值,其中P,Q的表達式詳見附錄．

3 過渡層材料性能沿徑向呈任意函數梯度變化

(18)

(19)

式(18)可改寫為

(20)

上式可看成是關于徑向位移的微分方程,其解可寫為

(21)

(22)

繼而聯立式(21)、(22),代入平衡方程(7),可得

(23)

(24)

其中

(25)

其中

(26)

(27)

h(r)為

4 數值算例與結果分析

假定功能過渡區域Ⅱ的材料性能按特殊冪函數形式變化,通過與第2節的精確解進行比較,可驗證第3節提出的Fredholm積分方程方法的有效性與精確度．同時本節主要運用Fredholm積分方程方法分析材料性能沿徑向呈Voigt函數變化時,梯度參數β、各向異性度λ、功能梯度區域的厚度t等對圓環結構整體所帶來的影響．

4.1 Fredholm積分方程方法的有效性與精確度的驗證

為驗證提出的Fredholm積分方程方法的有效性和精確性,本小節假設過渡層以特殊冪函數形式(9)變化,與得到的精確解進行對比驗證．區域Ⅰ的材料屬性為:

區域Ⅲ的材料屬性與梯度參數β有關

由于Poisson比的變化對應力與位移場的影響較小,因此假設夾層圓環各區域的Poisson比均為ν=0.3,此外假定外部荷載q0=0,角速度ω=100 rad/s,夾層圓環各區域內外徑分別為a/d=0.1,b/d=0.4,c/d=0.7,1．

特殊冪函數時由彈性力學理論求得的精確解與Fredholm積分方程方法得到的數值解對比結果如圖2所示,可以看出精確解與數值解完全重合,由此可以認為Fredholm積分方程方法不但具有精確性而且非常有效．

圖2 冪函數時數值解和解析解的比較Fig. 2 Comparisons of the exact and numerical results with the power law function (qn=ρⅢω2b2,

4.2 各向異性度對圓環結構應力與變形的影響

上述的驗證是通過在特殊冪函數的情況下與精確解比較來進行的,然而在實際工程結構中,夾層圓環材料的屬性隨其組成成分的變化而變化．接下來,我們將考慮更加一般的形式,假設夾層圓環的材料屬性沿半徑呈Voigt函數模型變化:

(28)

4.3 梯度參數對應力與位移場的影響

梯度參數β是夾層圓環結構過渡區域彈性模量的重要控制指標,β改變過渡區域的材料性能也將隨之變化．夾層圓環材料的其余參數設置參照4.2小節．圖4為梯度參數對結構應力場和位移場的影響．

圖4 梯度參數β對應力與位移場的影響Fig. 4 The influences of gradient parameter β on the stress field and displacement fields

由圖4(a)可知,隨著梯度參數β的增大,夾層圓環的徑向應力顯著減小且在各個區域之間徑向應力變化程度趨于平緩,對于各向異性材料來說,當β的值增大到一定程度時,徑向應力在區域Ⅰ與區域Ⅱ的值將變得很小,且徑向應力的最大值出現在區域Ⅲ中間的位置,這表明增大功能梯度參數對于改善夾層結構的徑向應力有明顯效果．由圖4(b)可知,隨著梯度參數β的增大,區域Ⅰ內環向應力與徑向應力變化一致,有著明顯減小的趨勢,且環向應力逐漸趨于零,然而在過渡區域Ⅱ內環向應力會發生明顯的增大現象,且在區域Ⅱ內大約在0.42的位置處隨著梯度參數β的增大環向應力也隨之顯著增大,在過渡層與區域Ⅲ的交界處環向應力達到最大值,隨之快速減小．這對設計各向異性材料來說也是需要特別關注的．由圖4(c)可知,隨著梯度參數β的增大徑向位移也隨之增大,與以往不同的是徑向位移的最大值不再出現在最外層邊界而是出現在過渡層區域．因此,可根據實際的需求通過調整夾層圓環的材料性能變化來進行優化設計．

4.4 過渡區域厚度對結構應力與位移場的影響

假定過渡層厚度參數為t(=(c-b)/d),通過固定區域Ⅰ的半徑((b-a)/d=0.2),調整t的大小來控制厚度參數,從而分析功能過渡區域的厚度變化對結構應力與位移場的影響．其余的夾層圓環材料屬性參數參照4.2小節,其中內層半徑為a/d=0.1．

由圖5(a)可以明顯看到隨著功能梯度過渡區域厚度t增大,夾層圓環整體的徑向應力也隨之減小,且徑向應力的變化趨勢逐漸減緩,對于最外層區域Ⅲ的變化趨勢影響不大,滿足邊界條件．從圖5(b)中可以看到隨著厚度參數t的增大,環向應力整體也隨之減小,環向應力在界面交界處出現的尖點明顯趨于平緩,雖然在接近最外層的區域隨著t的增大環向應力有增大的趨勢,但是變化不是很明顯．比較圖5(a)、5(b)可以發現隨著厚度參數t的增大,夾層圓環整體應力都有明顯的減小,表明增大功能梯度過渡區域厚度能夠有效減緩應力分布．由圖5(c)可以看出,隨著t的增大,徑向位移總體呈增大的趨勢．

圖5 功能過渡區域厚度參數t對應力場和位移場的影響Fig. 5 The influences of thickness parameter t in the functional transition region on the stress field and the displacement field

5 結 論

本文主要分析了帶有功能梯度過渡區域的夾層圓環在外層受均布壓力作用且以角速度ω繞剛性軸勻速轉動時的彈性場問題．當過渡層材料性能為特殊冪函數梯度形式變化時,得到了結構應力場與位移場的解析解．而對于過渡層沿徑向呈任意梯度形式變化時,采用積分方程方法將研究問題轉換為對關于徑向應力的Fredholm積分方程的求解．通過與特殊冪函數梯度形式得到的精確解進行對比,驗證提出的積分方程方法的有效性和精確性．在此基礎上,重點研究了過渡區域材料性能以Voigt函數梯度變化時不同參數對夾層圓環結構彈性場的影響．主要結論如下:

1) 梯度參數的增大可有效減緩徑向應力的分布,但會引起環向應力在過渡區域與區域Ⅲ的交界處的應力增大．

2) 各向異性度的增大會明顯降低夾層圓環的最大徑向應力,同時增加其最大環向應力以及徑向位移．

3) 隨著功能梯度過渡區域厚度增加,夾層圓環的應力變化趨勢明顯減緩,但徑向位移增大．

4) 提出的Fredholm積分方程方法適用于材料性能沿徑向呈任意梯度變化的情況,對于具體梯度變化情況只需代入相應梯度變化進行求解即可．

附 錄

精確解矩陣方程P,Q的表達式如下:

P=