插電混動汽車故障率研究

林 甄 陳奕健 謝金冶

（三亞學院，海南 三亞 572022）

0 引言

由于發展可靠性能夠很好地減少產品帶來的影響[1]，因此插電混動汽車的可靠性研究十分重要，隨著社會的飛速發展，人們的生活水平越來越好，消費需求更加旺盛，對產品的要求也越來越高。在國家大力提倡低碳出行、環保主義以及節能減排的背景下，插電混動汽車的到來無疑是雪中送炭[2]。

提高插電混動汽車的可靠性可以有效降低產品在整個壽命期間的費用。按照前期提出設想、規劃、設計到開始試驗、打造流程、試生產、運輸、儲存、使用、維修以及報廢過程中產生的費用，都可以通過可靠性的研究來降低[3]。

1 故障率研究內容

該文針對插電混動車輛在行駛過程中出現的問題進行研究分析，以威布爾理論分布為基礎，通過線性計算獲得完整的函數圖表，研究其損耗出現的原因以及如何減少勞損的方法等。

該文從安全性的基本理論出發進行概括性的闡述，進行整車的插電混合動車安全性的數據采集，包括線下走訪、網頁信息采集、對整理好的資料進行分析處理等。利用函數特性對工程可靠性理論進行分析，最終確定在實際工程中的適用范圍。

其中理論分布的計算和驗算以線上、線下采集的信息為準進行分組計算、查證，利用微軟旗下的軟件表格進行函數曲線圖表的繪制，得出整體的故障概率走向，研究其分布規律并應用到實際中，最終對其可靠度進行計算驗證。在此過程中可以利用現有的可靠性模型進行比對，建立一組具有插電混動汽車故障運行里程分布動態模型，其中包括損耗間隔里程概率密度模型、可靠度模型和消耗概率模型，并進行初始耗損期、特征虧耗期和損耗期的分析等[4-6]。

2 原始故障數據的獲取和分析

該研究主要采用線下采集信息法、線上收集法、大數據挖掘等方式收集研究資料。利用文獻分析梳理當前插電混動汽車大數據的研究現狀。1）線下調查信息收集法：走訪各個4S 店、汽車維修廠等。收集研究過程中所需要的新能源汽車的故障信息，進行統計、整理，得到數據。2）線上收集：通過互聯網瀏覽、搜尋插電混動汽車論壇、問卷調查、政府政策網頁與網站，查詢相關電子數字資料，從中獲得最新國外新能源汽車與大數據的動態信息。3）大數據挖掘：首先獲取經授權采集的汽車網站數據，通過URL 管理模塊對計劃爬取或已經爬取的URL 進行管理，然后利用網頁下載模塊對URL 管理模塊確定的URL 實施訪問下載，將下載的內容清洗數據并保存。

經過上述數據整理后，根據大數據分析系統獲得結果信息。具體數據見表1。

表1 故障數據表

從表1 可看出，行駛里程在3～4 萬km 時發生的故障最多；在5～6 萬km 后，車輛基本達到穩定狀態，沒有出現高頻率故障。可以得出行駛里程5～6 萬km 是車輛特征無故障工作里程，行駛里程3～6 萬km 是車輛中位無故障工作里程。

3 插電混動汽車的故障發展規律模型

3.1 理論分布參數估計

基于前面收集到的汽車信息，可以對插電混動汽車的故障行駛里程進行近似等于威布爾分布，即服從兩參數變量威布爾理論分布，通過觀察分布規律建立一組參數模型。

觀察規律演變時，應該先計算各個函數的分布值，通過計算結果和函數曲線圖像的對比研究其規律頻譜圖的走向。

函數分布值有賦值法、特值法的計算方法以及整除特性的思想。但在理論分布研究中最常采用回歸法。線性回歸分析是一個專門處理變量的統計關系問題的數理統計技術，是用來確定2 種及2 種以上分布函數關系的一種統計方法。將涉及的函數先進行線性化處理，兩邊連續取對數之后展開分析，計算得出之前假設的模型變量，其中公式定義來自于艾藝紅的概率論與數理統計[7]。

進行線性回歸后的相關計算如下所示。

三參數威布爾分布W（b，θ，m）的故障概率密度函數f（L）、分布函數F（L）與故障率λ（L）分別如公式（1）～公式（3）所示。

式中：b為形狀參數；θ為特征值，也稱為尺度參數。

3.1.1 線性回歸化

由可靠度R（L）與不可靠度F（L）的關系式R（L）+F（L）=1 可得公式（4）。

對公式（4）進行線性回歸化，兩邊連續取2 次對數可得公式（5）。

通過對原函數的線性回歸化，將原函數的參數估計轉化為對線性函數的參數b、A的估計。

3.1.2 參數估計

通過數列（xi，yi）（i=1，2，3，...，n，n=69），利用最小二乘法，運用Excel 軟件對函數關系式進行線性擬合，即可得出參數b、A的值。由公式（3）～公式（7）和表1 的各故障里程點L值可得出xi和yi，其中i=1，2，3，…，53。然后可以得出多組數列（xi，yi），擬合曲線圖如圖1 所示。

圖1 擬合曲線圖

擬合所得參數，b=0.769，A=2.7528，代入公式可得Θ=5.349。經理論分布假設檢驗后，可以判定故障發生里程數據服從威布爾分布的整體。

3.2 理論分布的假設檢驗

在3.1 節中，假設插電混動汽車故障數據的分布規律屬兩參數威布爾分布，然后對已知數據進行線性擬合，最終求出分布函數。

為了檢驗數據點符合擬合直線的程度，該文定義了擬合優度，如公式（9）～公式（11）所示。

式中：i=1，2，3，...，n，n=69；x、y與上節定義相同。

利用tn-2，1-a/2來確定臨界擬合優度rc2，如公式（11）所示。

式中：a為1 分布的顯著水平。

確定臨界擬合優度rc2與擬合優度r2之后，通過驗證是否滿足不等式r2>rc2來判斷y與x之間是否存在線性關系y=bx+A。

在新課程改革之前，傳統的教學模式以老師為中心，灌輸式地向學生傳授書本知識，導致學生在課堂上昏昏欲睡，課堂效率低下，這是因為傳統的教學觀念完全忽視了學生才是教學的主體，沒有考慮到學生接受知識的能力，因此，提高初中歷史課堂教學的效率，教師必須擺脫傳統教學觀念，更新歷史課堂的教學模式，為高效課堂的構建打下良好的基礎，歷史教師還應該具備現代化的教學理念，在高校課堂的教學中，以學生為中心，營造輕松的學習氛圍，激發學生對歷史的興趣，提升學生自主思考的能力，幫助學生養成良好的思維習慣，為學生之后的學習打下堅實的基礎。

計算得出=35，=3.6626，r2=0.91>0.9。

如果滿足檢驗要求，則可以判斷y與x之間存在的線性關系可信，可以判定故障發生里程數據服從威布爾分布的整體。

3.3 插電混動汽車故障分布規律的趨勢研究

故障分布規律的趨勢研究主要是以可信的理論分布得出相關的特征函數，如故障累計概率F（L）（既分布函數）、概率密度函數f（L）、失效率函數λ（L），繪制其總數居里程數的函數圖。

由3.2 節得出可靠性數據服從于二參數威布爾分布W（0.0769，5.349），并檢驗其可信。

3.3.1 故障分布趨勢分析

已知分布的參數，可得可靠度函數R（L）與故障分布函數F（L），如公式（12）、公式（13）所示。

故障概率密度函數f（L），如公式（15）所示。

3.3.3 故障率趨勢分析

根據理論模型，可得故障率函數λ（L），如公式（15）所示。

3.4 故障發展規律壽命周期分析

該文的可靠性特征量估計值為以下各項數值。1）特征壽命L0.37。根據特征壽命的定義和威布爾分布參數的意義，θ即為特征壽命，單位為萬km，根據計算可得L0.37=53490km。2）中位壽命L0.5。由可靠度關系式可知，里程點LR處的可靠度變換后可得。將R=0.5 時的里程值代入可得L0.5=9106km。3）可靠壽命L0.9=268km。4）平均故障間隔里程Lm。在該研究中，理論分布威布爾分布的概率密度函數f（L）為連續的+∝函數，則其中。當b=0.0769 時，由Γ 表可查出。代入參數，可得平均故障間隔里程Lm=44985km。

根據上文計算可靠性特征量估計值，通過這些數值可以將插電混動汽車的可靠性在量度方面進行評價，具體數據見表2。

表2 插電混動汽車可靠性特征量估計值

4 結論

該文首先對插電混動汽車現今所處地位以及未來的發展方向進行了概述，介紹了目前傳統燃油車、新能源汽車和插電混動汽車三者的發展情況，結合現在環境問題以及能源危機的大背景討論發展插電混動汽車的重要性以及提高汽車可靠性的意義。

其次，分析可靠性工作中數據處理的關鍵作用。按照以往的工作經驗，可靠性數據的分布規律通常都可以用某些科學方法進行近似分析，而運用上述科學分布法可以針對實際工作問題進行可行性分析，論述了可信度研究工作中最常見的4 個科學方法：指數分布、正態分布、對數正態分布和威布爾分布（包括三參量與二參數）。利用威布爾二參數檢驗插電混動車輛故障發展變化規律，并對線性參量的回歸化、模型擬合優度和臨界模型擬合優度對特征量數據和所使用的樣本數據的處理，得出汽車故障演變規律與里程L服從于威布爾分布。

分析收集到的69 條數據，最終得出插電混動汽車故障發生情況如圖2 所示。可以看出與發動機有關的故障發生概率最大，總共出現18 次，其次就是與電機有關的。插電混汽車的故障規律主要體現在以上2 點。

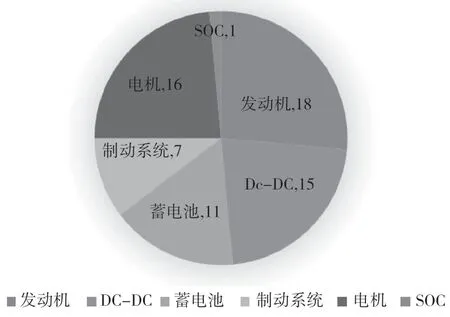
圖3 故障規律分布圖