機器故障下的柔性作業車間調度優化

劉道興

（山東科技大學，山東 青島 266590）

0 引言

車間調度問題最早是由JOHNSON 在20 世紀50 年代提出的[1]，到了20 世紀90 年代BRUCKER 擴展了車間調度理論，提出柔性作業車間調度（Flexible Job-shop Scheduling Problem，FJSP）[2]，隨后眾多學者又在FJSP 問題上加入了動態擾動，研究在擾動條件下的車間調度問題。

隨著計算機技術的快速發展，啟發式算法為解決FJSP問題提供了更好的思路，也逐漸取代了傳統的調度規則和數學類方法。陳鴻海等[3]、尹愛軍等[4]、景志強等[5]、曾強等[6]對非支配排序遺傳算法進行改進研究，解決了相關的車間調度問題，并證明各自的改進在解決調度問題上的可行性。陳魁等[7]利用小生境粒子群優化算法解決了考慮工件運輸時間的多目標FJSP 問題。趙博選等[8]使用基于多策略融合的Pareto 人工蜂群算法求解多目標的FJSP 問題。

該文將機器故障下的柔性作業車間調度問題分為2 個階段：首先，采用智能算法求解出靜態預調度方案。其次，在靜態調度方案基礎上提出了基于2 種重調度策略的組合重調度策略，并驗證了該策略在解決機器故障下的FJSP 問題的可行性。

1 問題描述

該文將考慮機器故障的FJSP 問題分為2 個過程，首先是傳統的靜態FJSP 問題，其次是在靜態調度方案基礎上發生機器故障后的重調度。

FJSP 問題的具體描述如下：有n個工件在m臺機器上加工，工件的工序數和加工工藝已經確定無法改變，并且所有工序在可選機器上的加工時間是確定的，選擇不同機器的加工時間也不盡相同。調度的目的就是通過調整工序的加工順序和選擇加工機器找到更優的加工方案，以實現各項優化目標，所有工件生產完成后即調度結束。

研究FJSP 問題時要與實際生產狀態相匹配，需要提出以下假設條件：第一，開始時，所有的機器都處于待機狀態，且工件加工只能選擇一臺機器。第二，工藝順序為確定順序，在加工時不能發生改變，該工件的前道工序加工完成后才能對后道工序進行加工。第三，出現設備故障時，受到影響的機器停止加工，未受到影響的機器繼續加工。第四，發生設備故障時，故障在一定時間內可以維修恢復。第五，工序時間包括加工時間和工作準備時間。第六，工件能在可加工機器上任意切換。第七，前、后工件之間沒有約束關系。

2 模型建立

從最小加工總時間、最小機器總能耗、最小機器總負載3 個角度建立柔性作業車間調度優化模型。

2.1 最小加工總時間

最小加工總時間指的是最后一道工序加工完成后花費的總時間最短，是調度方案效率最直接的體現，如公式（1）所示。

式中：i為工件號；ti為工件i的加工時間。

2.2 最小機器總能耗

最小機器總能耗指的是從加工開始到所有工件加工完成機器所消耗的能源最小（包括空載與負載），如公式（2）所示。

式中：j為工序號；qi為工序數；z為機器號；m為機器數；Tijz為工件oij在機器z上的加工時間；oij為工件i的第j道工序；Xijz為決策變量，當工件i在機器z上加工為1，否則為0；Lz、ULz分別為機器z在負載下的能耗與空載下的能耗；CTz為oij在機器z上的完工時間。

2.3 最小機器總負載

總負載最小是指工件在機器上的加工時間最小，其計算如公式（3）所示。

3 問題求解

3.1 靜態FJSP 問題求解

針對靜態的多目標FJSP 問題，該文采用改進的灰狼優化算法進行求解。狼優化算法（GWO）是2014 年由澳大利亞學者提出的一個群智能優化算法[9]，其主要是模擬狼群的捕獵過程，具有收斂性強、參數少和易實現的特點，在求解車間調度問題上具有很大優勢。但是該算法本身也存在一定缺陷。首先，GWO 作為非精確算法，在求解迭代過程中需要挑選一個或多個優秀個體去引導目標優化的方向，而FJSP問題涉及目標較多，個體優劣判斷較難，會直接影響算法性能，因此需要采用孫新宇等[10]提出的方法，即引入非支配排序及擁擠度計算，以此來判斷算法中的個體優劣。其次，針對GWO 線性收斂易造成局部最優解的問題，在孫新宇法改進的基礎上，該文采用了一種非線性收斂因子，避免算法出現局部最優解的問題。

3.1.1 非支配排序及擁擠度計算

采用孫新宇提出的方法，引入非支配排序及擁擠度計算，經過快速非支配排序和擁擠度計算，得到種群中每個個體的非支配序和擁擠度，當且僅當個體i的非支配序大于等于個體j且個體i的擁擠度大于個體j，可得個體i優于個體j。

3.1.2 改進非線性收斂因子

作為群體智能算法，GWO 法有全局搜索和局部搜索2個過程，二者的平衡關乎算法收斂速度，進而影響算法求解的性能。在GWO 中，收斂因子a決定了算法是實現全局搜索還是局部搜索。傳統的GWO 中，a隨迭代從2 線性遞減至0，但實際求解問題時算法的迭代常常不是呈線性的。在迭代初期，收斂因子a應當緩慢衰減，以保證算法實現全局搜索，找到更好的全局解。到了算法迭代后期，收斂因子a應當快速衰減，以保證算法在局部搜索，進而更加準確地找到局部內的最優解。此情況下的a線性收斂策略將無法滿足算法迭代規律[11]，因此該文改進了收斂因子a的收斂方式，采用一種非線性收斂方式，如公式（4）所示。

式中：e 為自然數；t為迭代次數；tmax為最大迭代次數。

3.1.3 算法流程

改進后的灰狼優化算法步驟如下。步驟1：設置種群數量、算法參數以及種群迭代次數；步驟2：初始化種群；步驟3：解碼得到優化目標的參數；步驟4：根據得到的優化目標參數進行非支配排序和擁擠度計算；步驟5：計算后用灰狼算子更新種群；步驟6：計算個體的適應度，最優的3個為α、β、δ三只狼；步驟7：判斷算法是否達到最大迭代次數，是則輸出結果，否則轉到步驟4。

3.2 機器故障下的重調度求解

在靜態預調度方案的基礎上，當發生機器故障時，需要及時調整調度策略，以保證生產的穩定進行。該文針對機器故障下的調度策略的調整，采用重調度策略代替單一重調度策略，并結合2 種調整策略的特點，保證在不同情況下重調度策略的適用性。

3.2.1 右移重調度策略

發生機器故障后，直接調整故障機器上正在加工的工序或者將要在故障機器上加工的工序，直到機器可以加工工件，即為右移重調度策略。具體步驟如下：首先，確定故障機器、故障發生時間和故障修復時間。其次，分析確定出預調度中在故障機器上直接加工或者將要加工的工序集合。最后，根據故障的修復時間，將受到影響的工序右移，直到故障修復，滿足工件的加工條件后開始加工，形成右移重調度方案。

3.2.2 完全重調度策略

當機器發生故障時，將方案切分，故障前的加工工序不變，將故障后所有機器待加工的工件完全重組，重新編碼解碼，得到新的調度方案，即為完全重調度策略。具體步驟如下：首先，找到故障發生時間進行切分，確定未開始的需要重新調度的工序集合，其中包括中斷的工序和沒有開始加工的工序。其次，確定所有機器的開工時間，機器的開工時間為故障發生后的最早空閑時間。最后，采用智能算法對確定好的工序合集進行編碼解碼，得到新的調度方案，與切分的調度前半部分方案組合即為故障發生后的完全重調度方案。

3.2.3 重調度流程

在重調度階段，為了探究在不同情況下如何選擇重調度策略，并探究組合重調度策略是否優于單一重調度策略，對2 種重調度策略分別進行求解試驗。然后將結果進行對比，選取較優的方案作為最終的重調度方案。

4 仿真結果與分析

為了驗證方案求解機器故障下FJSP 問題的可行性，采用標準車間調度數據MK01。該算例是一個工件數為10、機器數為6 的10×6 算例。

4.1 靜態預調度方案

仿真試驗的運行環境為Intel Core i7 CPU，主頻2.60GHz，內存16GB，Windows 11，64 位操作系統，試驗仿真軟件為Python3.6.5，種群大小為100，進行150 次迭代，得到的預調度結果圖如圖1 所示，排產的甘特圖如圖2 所示。

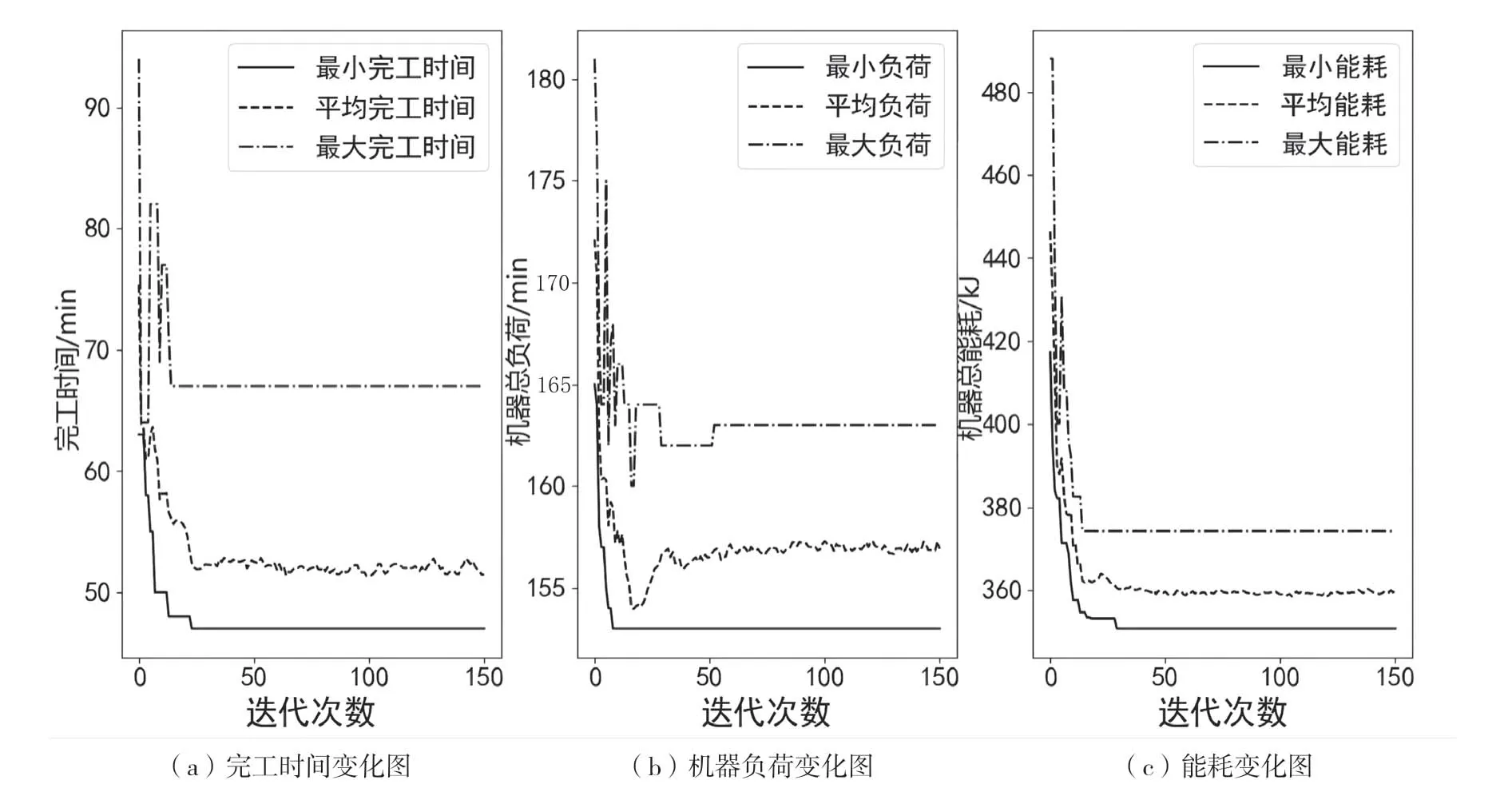
圖1 改進灰狼優化算法目標函數結果圖

圖2 中的矩形方塊代表算法中工件的解碼，即工件加工的順序，其中的數字代表工件號，某工件按照時間順序出現的次數代表該工件的第幾道工序。部分加工順序的舉例如圖3 所示。機器3 中第一個矩形方塊中的數字1 代表工件1 的第一道工序，機器6 中第一個矩形方塊10 則為工件10 的第一道工序，而機器3 第2 個方塊中的10 為第二次出現，則為工件10 的第二道工序。依此類推，解碼得到排產的加工順序，即為可行的靜態調度方案，具體如下。

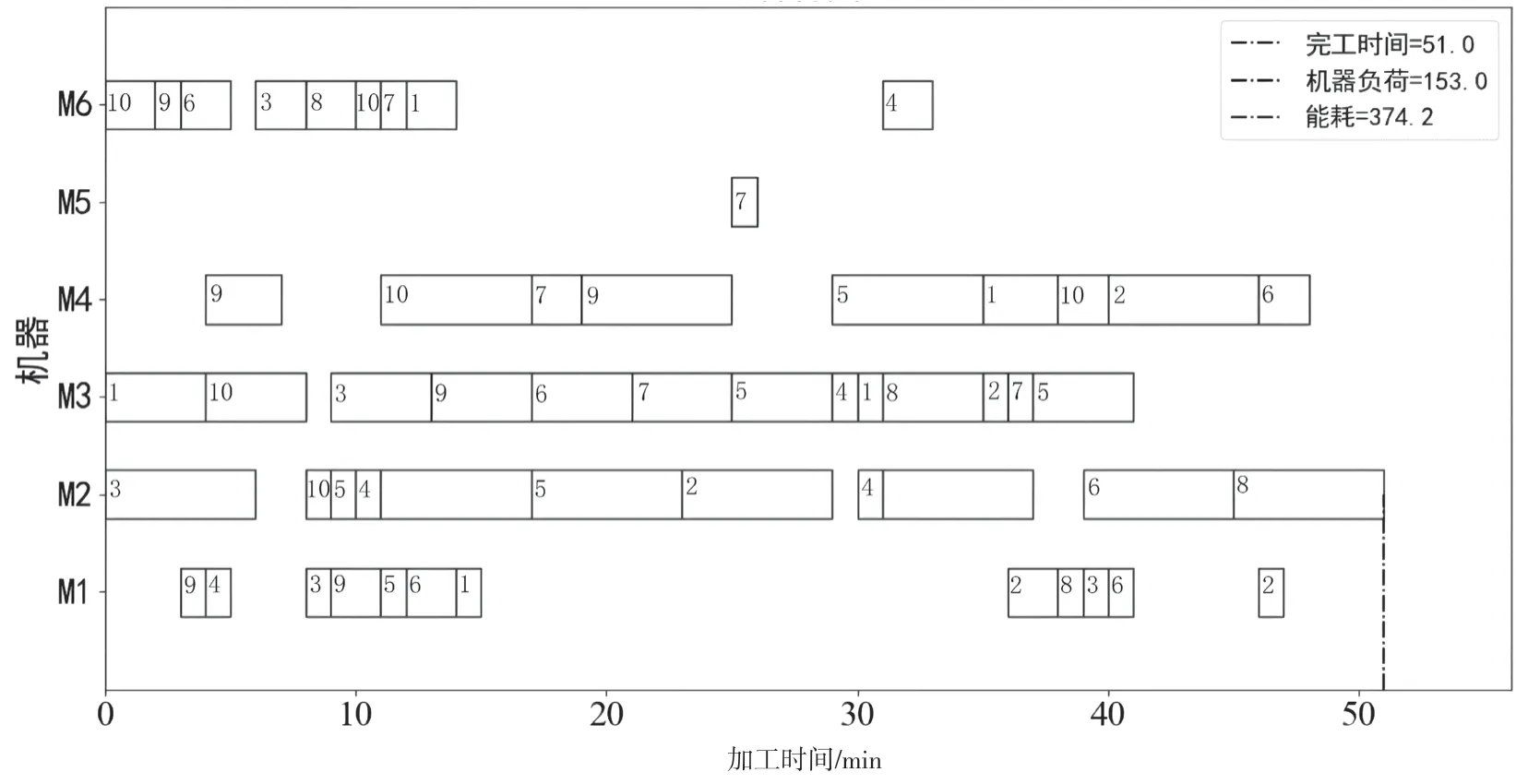
圖2 改進灰狼優化算法MK01 甘特圖

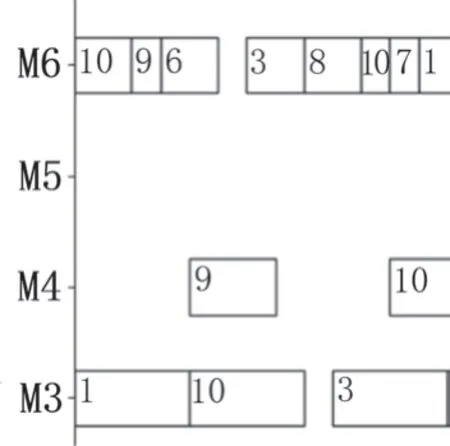
圖3 排產甘特圖（局部）

預調度工序集：

預調度工序集對應機器集：

預調度工序集對應機器加工時間集：

4.2 重調度方案

為驗證加工機器對加工的影響，本試驗在預調度的方案基礎上選取機器3 在第15min 發生故障，故障持續時間為6min，在不同的重調度策略下得到的排產甘特圖如圖4、圖5所示。

圖4 機器3 故障下右移重調度甘特圖

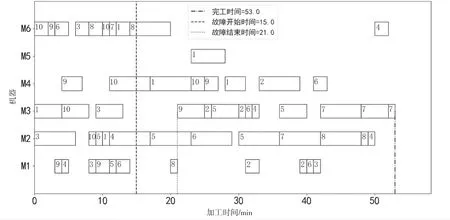
圖5 機器3 故障下完全重調度甘特圖

從重調度排產甘特圖可得，當故障發生在對后續工件加工影響較大的機器3 上時，完全重調度策略要優于右移重調度策略。采取同樣的調度策略，當故障發生在機器5 對工件加工影響較小的機器且故障持續時間依舊為6min 時，右移重調度策略的完工時間為51min，而完全重調度策略的完工時間為54min，此時右移重調度策略要優于完全重調度策略。

綜上所述，進行重調度時，如果只采用某一種重調度策略，可能在不同條件下會缺乏適應性，因此采用2 種重調度的組合策略，在不同條件下選擇不同策略進行重調度，才能保證生產的高效進行。

5 結語

該文將機器故障下柔性作業車間調度問題分為靜態預調度和機器故障下的重調度2 個部分。首先，采用了改進的灰狼優化算法，計算得到靜態預調度方案。其次，基于右移重調度策略和完全重調度策略的特點，提出了一種組合重調度策略，驗證了其比單一重調度策略在解決生產調度問題上更具適應性。

目前該文只考慮了2 種重調度策略，下一步工作需要挖掘更加完善的重調度策略，以提高重調度方案在解決動態調度方面的適應性。