研讀標準·理解本質·構建體系·發展思維
——2022年中考數學試題命題分析及復習教學建議

謝 慧，李 巖

（北京市朝陽區教育科學研究院；北京市日壇中學）

2021年7月，中共中央辦公廳、國務院辦公廳印發了《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》.在此政策背景下，2022年全國各地區中考數學試卷的命制結合自身特點，緊密聯系教材，充分挖掘教材中適切的素材，發揮考試命題助推政策落地的作用，引導教學回歸課堂，引導教師發揮課堂的教學主渠道作用.從整體上看，2022年中考數學試題的命制以落實立德樹人為根本任務，以《義務教育數學課程標準（2011年版）》（以下簡稱《標準（2011年版）》）為依據，體現《義務教育數學課程標準（2022年版）》（以下簡稱《標準（2022年版）》）的素養目標，以教材為抓手，適度創新，把控難度，發揮試題育人功能；立足課堂教學實際，緊扣學科本質，突出學習過程，考查數學思維，關注數學核心素養.

一、總體情況分析

2022年全國各地中考數學在試卷結構、題型分布、分數設置等方面均保持穩定，依據《標準（2011年版）》規定的課程目標與課程內容命題，考查主干知識、核心能力和基本思想方法.試卷合理搭建難度梯度，試題表述和設問與學生學習經驗一致，易于學生理解，有利于不同水平的學生作答，營造了良好的教育教學評價環境.結合數學學科自身特點，選取源于學生生活及與社會經濟發展有關的素材，將社會主義核心價值觀自然融入試題中，發揮試題的育人功能.

初中階段的數學課程內容由“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”四個領域組成.從調研的2022年全國各地區151份中考數學試卷可以看出，各地均能夠以基礎知識和基本技能為載體考查學生的關鍵能力和數學核心素養.統計的151份試卷中，以考查“數與代數”“圖形與幾何”“統計與概率”三個領域為重點，試題數量分別為2 001道，1 222道，621道（含有知識重疊），重點考查知識之間的內在聯系和整體結構，與教材內容和呈現形式相一致.另外，有45份試卷將綜合與實踐或融入試題中，或進行獨立命題，較2021年中考而言有大幅度的提升.可見，2022年中考數學命題極大地關注了學生學習過程的地位和作用.

“數與代數”領域是從數及其運算，到代數式及其運算，再到方程（組）和解方程（組）、不等式（組）和解不等式（組），再到函數逐步發展的.52份試卷中單獨考查了數及其運算，如江蘇徐州卷、湖北黃石卷、山東濟南卷等；共234道題涉及代數式及其運算，多以選擇題、填空題、計算題為主，考查內容主要為列代數式、整式運算、因式分解、分式運算、二次根式的意義及運算.“方程與不等式”部分的495道試題中有約40%考查實際問題，凸顯了數學的應用價值.函數是“數與代數”領域的主干知識，調研的2022年全國各地區151份中考數學試卷中共有679道題涉及函數問題.函數是研究事物運動變化規律的數學模型，它既來源于生活又服務于生活，即從生活實際中抽象出函數的有關概念，再運用函數知識解決實際問題.函數的圖象與性質是函數內容研究的主體，通過對函數圖象的研究，從圖形和數量兩個角度及其相互聯系中，凸顯出函數的本質特征是聯系和變化.這既是函數教學的主線，又是函數學習的主線.例如，江蘇南通卷第24題、吉林長春卷第21題、山東臨沂卷第20題等用圖象刻畫實際生活中變量之間的函數關系；山東淄博卷第20題、遼寧阜新卷第18題、內蒙古呼和浩特卷第21題等利用數形結合的思想方法研究反比例函數、一次函數和二次函數的圖象與性質；北京卷第25題、湖北襄陽卷第14題、浙江衢州卷第23題等都是將實際問題抽象成函數模型后，利用二次函數的圖象與性質解決問題.

“圖形與幾何”領域以發展學生的空間觀念、幾何直觀、推理能力為核心，通過研究基本幾何圖形的性質，積累有關知識與經驗，借助幾何直觀，運用推理探索圖形變化的性質，發現在運動變化過程中圖形中的不變量與不變關系，并建立圖形與坐標的關系.其中，涉及三角形、多邊形、圓等重點圖形的試題數量分別為707道，476道，389道，總體較2021年略有提高.其中，多邊形和圓兩部分試題數量基本不變，可見對于三角形這個基本圖形的考查力度有所增加.2022年，有更多地區的中考數學試卷對“圖形與幾何”領域的考查難度有所降低，在回歸基礎、突出本質、強化思維與表達、創設情境、滲透育人價值等方面都做了有益的探索，試題設計適當降低了基本圖形結構的復雜程度.以尺規作圖角度進行考查的試題從2021年的29道上升到51道，可見越來越多的地區關注到了作圖是幾何學習的重要手段和重要過程，這也是邏輯的起點和思維的開始.例如，遼寧營口卷、河北卷都命制了從圖形運動變化的角度通過操作、觀察、猜想得到結論，再用演繹推理證明其結論成立的試題；北京卷第28題從圖形與坐標關系的角度出發，引導學生探究運動變化過程中圖形的不變量與不變關系.

“統計與概率”領域重點突出對統計全過程的考查，在數據的收集、整理和描述的基礎上，考查了平均數、眾數、方差在分析數據分布情況時的作用，以及樣本估計總體的思想，著重考查了學生對數據進行分析和利用數據中提供的信息解決問題的能力.2022年大部分地區中考數學試卷中相關試題的命制取材于學生生活、學習中的常見情境，與學生學習的過程和經驗一致.學生在經歷統計的全過程中，樹立數據觀念，發展運用統計思想解決問題的能力.調研的151套2022年中考數學試卷中，統計專題中有182道試題考查數據的收集與整理，其中有19道題考查了調查的方式，有174道題結合統計圖表考查數據分析，如山東棗莊卷第19題考查了“數據調查—數據收集與整理—數據分析”的全過程；概率專題中，寧夏卷第22題、廣西桂林卷第22題、甘肅蘭州卷第21題等考查了用頻率估計概率的相關問題，其他地區的試卷中大多考查用列舉法求概率，如江蘇鎮江卷第21題、遼寧鞍山卷第20題等.

二、命題立意與導向

1.扎實基礎，落實“四基”要求

由于初中學業水平考試具有考查學生完成義務教育階段數學課程學習的達標性考核功能.因此，數學的基礎知識與基本技能是初中學業水平考試考查的重要方面.從對2022年全國各地區中考數學試題的分析可以看出，其從數學學科角度考查了最基礎和最重要的部分；從義務教育性質的角度考查了課程目標所涉及的基本要求.

“數與代數”領域的基礎內容主要涉及三大類：對象——數、字母（常量、變量）；運算——四則運算、乘方與開方運算、式的運算；關系——數量關系（相等與不等）、函數關系.在數學教學過程中，它們多以概念、原理、法則的形式出現.

例1（山東·日照卷）下列運算正確的是（ ）.

（A）a6÷a2=a3（B）a4·a2=a6

（C）（a2）3=a5（D）a3+a3=a6

答案：B.

例2（江蘇·鎮江卷）“五月天山雪，無花只有寒”，反映出地形對氣溫的影響.大致海拔每升高100米，氣溫約下降0.6℃.有一座海拔為2 350米的山，在這座山上海拔為350米的地方測得氣溫是6°C，則此時山頂的氣溫約為______.

答案：-6°C.

例3（遼寧·鞍山卷）先化簡，再求值：，其中m=2.

當m=2時，.

考查目標：例1～例3考查冪的運算和正負數的意義，以及分式的運算.

命題意圖：例1源于教材，是一道立足整式的核心知識，考查學生運算能力的基礎試題.四個選項的設計涉及同底數冪的運算、冪的乘方、整式加減運算，體現了對學生扎實運算基本功的關注.例2通過與現實生活聯系，考查正負數的意義及有理數的混合運算.正確理解試題的含義，準確進行計算是解題的關鍵，體現了數學源于生活又應用于生活.例3考查“數與代數”中的代數式及其運算，涉及整式與分式部分的內容，要求學生通過分式的加、減、乘、除運算對代數式進行化簡，考查學生的運算能力.

命題評價：此類試題屬于對基礎知識和基本技能的考查，主要體現對學生運算能力的考查.充分理解運算對象、準確求得運算結果是學生需要掌握的必要技能.

“圖形與幾何”領域的基礎內容主要涉及三大類：對象——點、線、面（角、線段），平面圖形（多邊形、圓），坐標；性質——單個圖形在形狀、度量、變化、位置等方面的性質；關系——兩個對象之間的關系，如平行和垂直，全等、相似和對稱，距離、大小和位置等.

例4（北京卷）下面幾何體中，是圓錐的為（ ）.

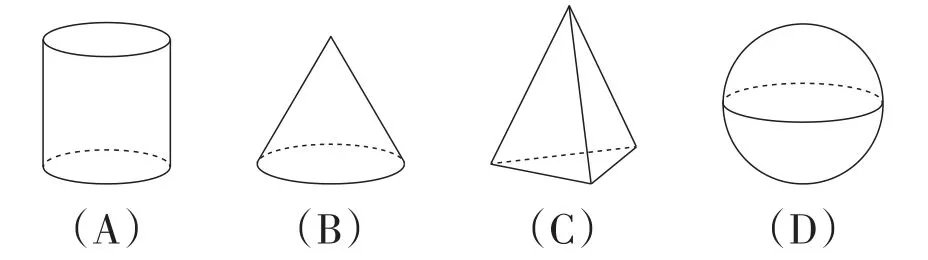
答案：B.

例5（江蘇·常州卷）下列圖形中，為圓柱的側面展開圖的是（ ）.

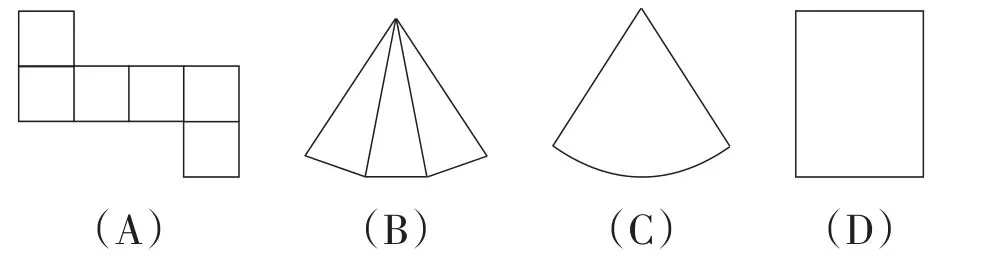
答案：D.

考查目標：例4和例5要求學生能識別立體圖形及其展開圖.

命題意圖：初中階段，“圖形與幾何”領域的內容主要涉及平面幾何，高中階段則是解析幾何和立體幾何.從初、高中銜接的角度考慮，初中階段涉及的立體圖形的有關內容是命題時主要選擇的知識載體，所以這類試題是學生會做且內涵豐富的試題.

命題評價：例4考查立體圖形，例5考查立體圖形的展開圖.以上兩道題貫徹了《標準（2011年版）》中“通過實物和具體模型，了解從物體抽象出來的幾何體、平面、直線和點等”的要求.

例6（湖北·十堰卷）如圖1，工人砌墻時，先在兩個墻腳的位置分別插一根木樁，再拉一條直的參照線，就能使砌的磚在一條直線上.這樣做應用的數學知識是（ ）.

圖1

（A）兩點之間，線段最短

（B）兩點確定一條直線

（C）垂線段最短

（D）三角形兩邊之和大于第三邊

答案：B.

例7（山東·臨沂卷）如圖2，A，B位于數軸上原點兩側，且OB=2OA.若點B表示的數是6，則點A表示的數是（ ）.

圖2

（A）-2 （B）-3 （C）-4 （D）-5

答案：B.

考查目標：例6考查學生用兩點確定一條直線、兩點之間線段最短等基本事實解釋生活問題的能力；例7考查直線和數軸的相關概念.

命題意圖：《標準（2011年版）》中明確要求學生會比較線段的長短，理解線段的和、差，以及線段中點的意義，掌握兩點確定一條直線、兩點之間線段最短等基本事實.兩道試題都考查了學生對直線相關概念的理解.

命題評價：例6是對基本事實的考查，要求學生能夠運用數學原理解釋生活現象，題面簡潔、明確，素材基本來源于教材，是學生熟悉的情境，落實了基本數學活動經驗.例7借助數軸考查線段的數量關系和數形結合思想，體現了“學考合一”，是學生應知必會的核心知識.

例8（北京卷）如圖3，在?ABCD中，AC，BD交于點O，點E，F在AC上，AE=CF.

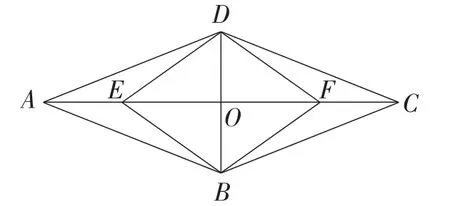
圖3

（1）求證：四邊形EBFD是平行四邊形；

（2）若∠BAC=∠DAC，求證：四邊形EBFD是菱形.

答案：略.

考查目標：此題考查學生運用平行四邊形的性質與判定、菱形的判定定理解決簡單問題的能力.

命題意圖：此題以特殊平行四邊形為考查主體，通過圖形與圖形之間的全等關系，結合三角形、四邊形等圖形的基本性質，考查圖形與圖形之間的邏輯關系.此類試題具有一定的綜合性，通常以中檔題為主，解答題居多.其中也充分體現了對應思想、轉化思想和模型觀念.

命題評價：此題為綜合性幾何證明題，定位恰當、難度適中，要求學生具備探尋條件與結論之間邏輯關聯的思維能力，符合《標準（2011年版）》的要求.第（1）小題中，證明四邊形EBFD是平行四邊形，既可以運用全等三角形的性質，也可以利用平行四邊形的性質，體現了平行四邊形性質的簡潔性，是“圖形與幾何”領域的核心內容.第（2）小題添加條件后，要求進一步證明四邊形EBFD為菱形.兩道小題之間有內在的邏輯聯系，考查學生對平行四邊形和菱形的性質，以及它們之間的知識聯系的掌握情況，特別是對四邊形的對角線性質進行了關注，考查了學生在合情推理、演繹推理等方面的發展水平.此題的考查角度與學生開展學習的過程相一致，能夠引導教師在教學的過程中鼓勵學生對已經學習的幾何定義、性質、判定串聯成線，形成知識結構網絡.

“統計與概率”領域的基礎內容主要涉及兩大類：對象——數據、概率（頻率）；意義——統計量的計算及推斷，概率的計算.統計部分涉及的內容主要包括數據的收集、表示、處理，數據統計量的計算及其意義.部分地區中考試題的命制關注了統計全過程的體現和統計圖表的運用，要求學生借助常見的真實背景分析具體數據之間的關系，給出適當的方案，提出決策；概率部分包括概率的含義、簡單古典事件概率值的計算等.這類試題中涉及的背景多為純數學或簡單的實際背景，且結構簡單，主要用于考查學生對相關基礎知識和基本技能的掌握情況.

例9（江蘇·徐州卷）如圖4，下列裝在相同的透明密封盒內的古錢幣，其密封盒上分別標有古錢幣的尺寸及質量.例如，錢幣“文星高照”密封盒上所標“45.4*2.8 mm，24.4 g”是指該枚古錢幣的直徑為45.4 mm，厚度為2.8 mm，質量為24.4 g.已知這些古錢幣的材質相同.

圖4

根據圖中信息，解決下列問題.

（1）這5枚古錢幣，所標直徑的平均數是____，所標厚度的眾數是_____，所標質量的中位數是_____；

（2）由于古錢幣無法從密封盒內取出，為判斷密封盒上所標古錢幣的質量是否有錯，桐桐用電子秤測得每枚古錢幣與其密封盒的總質量如表1所示.

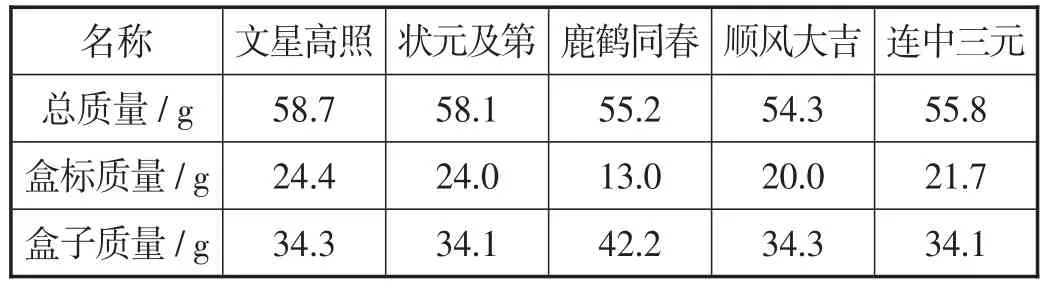
表1

試應用所學的統計知識，判斷哪枚古錢幣所標的質量與實際質量差異較大，并計算該枚古錢幣的實際質量約為多少克.

答案：（1）45.74，2.3，21.7；

（2）“鹿鶴同春”的實際質量約為21.0 g.

考查目標：此題要求學生能夠理解平均數、中位數、眾數等統計量的概念和統計意義.

命題意圖：此題以中國古錢幣為背景，考查學生的統計相關知識、數據統計意識，以及運用統計數據進行推斷和決策的能力.

命題評價：此題以基本的統計知識（平均數、中位數、眾數等）為考查載體，通過實際問題引導學生體會基本統計方法，即收集數據、整理數據、描述數據、分析數據、應用數據，并運用所得數據進行推斷和決策，體現了基本統計思想.這是統計學習的本質要求，同時也引導學生在解決問題過程中體會“統計是進行判斷、決策的有效手段”.尤其是對平均數含義的考查，體現了統計在生活中的作用.

從以上三個領域的考查可以看出，2022年中考數學試題大多能體現初中學業水平考試的要求，在考查基礎知識和基本技能的同時注重落實對基本活動經驗、基本數學思想的考查；注重試題設問角度的創新性，設問方式的開放性，思維的層次性和發展性，以及試題的應用性及育人功能，凸顯素養立意.

2.突出過程，重視知識本質

2022年全國各地區中考數學試卷除了考查知識外，更多關注了知識的生成過程與學生的學習過程，考查角度體現了從“知其然”到“知其所以然”的轉變，部分地區中考試卷的考查指向了“何由以知其所以然”.除了關注學生對結論的理解、記憶，也關注了獲得結論的方式、方法及學習的全過程.通過對知識學習過程的考查，引導教學關注知識本質，加強學生對數學知識的理解，通過對數學本質的思考，更好地理解實際生活，解釋實際生活中的現象.

例10（北京卷）下面是證明三角形內角和定理的兩種添加輔助線的方法，選擇其中一種，完成證明.

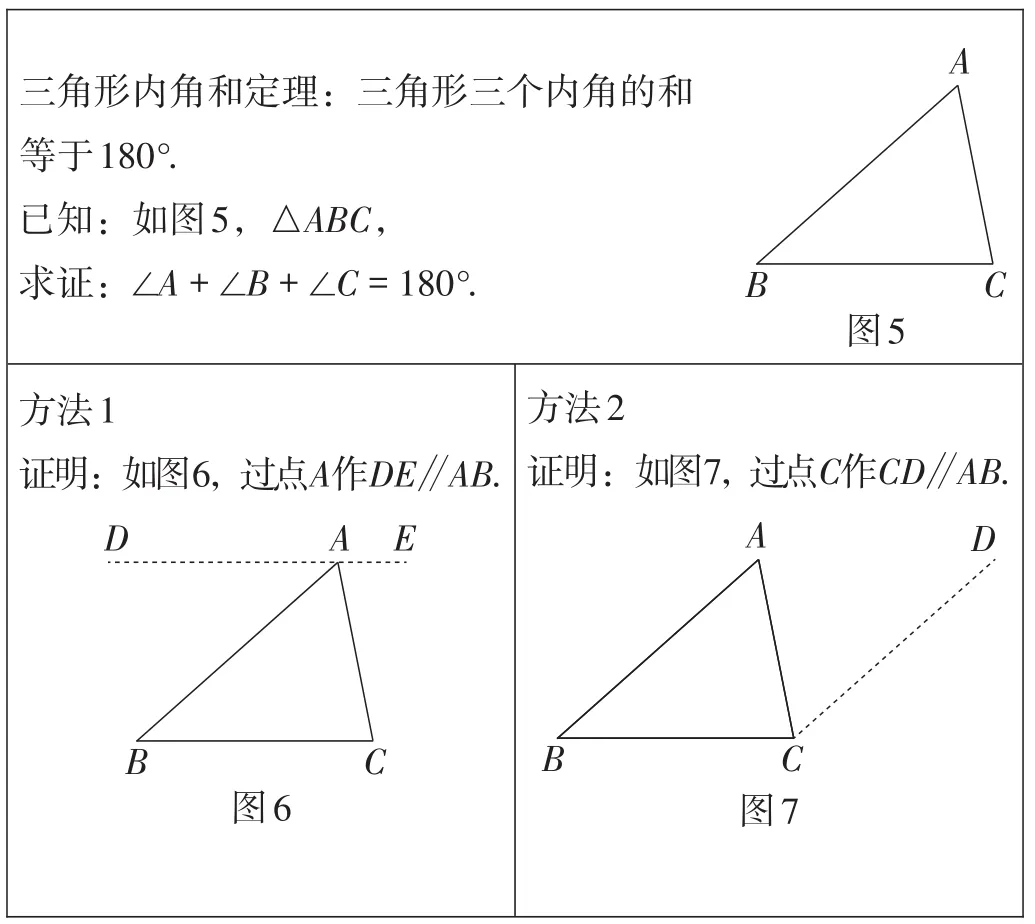
考查目標：此題要求學生能證明三角形內角和定理，以及運用平行線的性質解決簡單的問題.

命題意圖：此題考查三角形內角和定理的證明，素材來源于教材，體現了知識的形成過程和研究過程，旨在引導教師的教和學生的學不僅要關注結果，更要關注形成結果的過程.此題給出了兩種不同的輔助線添加方式，學生可以自主選擇其中一種進行證明，體現了鼓勵學生從多個角度思考問題的教學導向，同時尊重和鼓勵學生的自主選擇權.

命題評價：三角形是學生在初中階段的幾何學習中第一次對一個圖形進行系統性學習，三角形內角和定理的證明也是學生第一次接觸完整的邏輯推理過程，第一次接觸添加輔助線.如何將小學階段的學習經驗和操作經驗轉化為邏輯推理的過程，充分體現了通過輔助線達到轉化問題的目的，其中也蘊含了圖形的運動變化.

例11（北京卷）單板滑雪大跳臺是北京冬奧會比賽項目之一，舉辦場地為首鋼滑雪大跳臺，運動員起跳后的飛行路線可以看作是拋物線的一部分.建立如圖8所示的平面直角坐標系，從起跳到著陸的過程中，運動員的豎直高度y（單位：m）與水平距離x（單位：m）近似滿足函數關系y=a(x-h)2+k(a＜0).

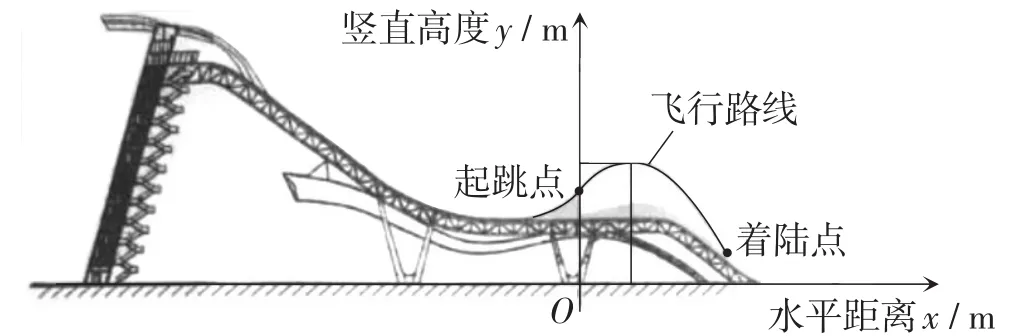
圖8

某運動員進行了兩次訓練.

（1）第一次訓練時，該運動員的水平距離x與豎直高度y的幾組數據如表2所示.

表2

根據上述數據，直接寫出該運動員豎直高度的最大值，并求出滿足的函數關系y=a(x-h)2+k(a＜0 )；

（2）第二次訓練時，該運動員的豎直高度y與水平距離x近似滿足函數關系y=-0.04(x-9)2+23.24.記該運動員第一次訓練的著陸點的水平距離為d1，第二次訓練的著陸點的水平距離為d2，則d1________d2（填“＞”“=”或“＜”）.

答案：（1）該運動員豎直高度的最大值為23.20 m.函數關系式為y=-0.05(x-8)2+23.20.

（2） ＜.

考查目標：此題要求學生能夠根據給定坐標求出滿足關系的二次函數關系式，能運用二次函數的圖象和性質解決實際問題.

命題意圖：此題考查了函數學習的全過程.全國各地區中考對于函數的重視程度明顯提高，類似考查角度的試題還有河南卷第21題、江西卷第22題、湖北武漢卷第22題、浙江臺州卷第24題等.

命題評價：此題以北京冬奧會單板滑雪大跳臺比賽為背景，要求學生分析運動變化的過程，建立函數模型求解.第（2）小題要求學生比較水平距離，方法靈活多樣，可計算比較，可畫圖比較，也可以通過分析拋物線開口變化來比較.不同的方法體現了學生的不同思維水平.能夠理解函數圖象變化本質與解析式中自變量的系數有直接關系的學生可以通過幾何直觀、邏輯推理等多種角度解決此問題.

3.關注情境，重視文化傳承

情境是學生理解數學知識的基礎，也是發展學生數學抽象和數學建模能力的重要途徑之一.2022年全國各地區中考試題在情境設置方面，關注了時代性、跨學科性、應用性，反映了現代科技成果和時代的進步，同時凸顯了情境的公平性和數學本質蘊含的豐富性，以及與試題設問的匹配性.

例12（山東·棗莊卷）北京冬奧會開幕式的巨型雪花狀主火炬塔的設計，體現了環保低碳理念.如圖9，它的主體形狀呈正六邊形.若點A，F，B，D，C，E是正六邊形的六個頂點，則tan∠ABE的值為______.

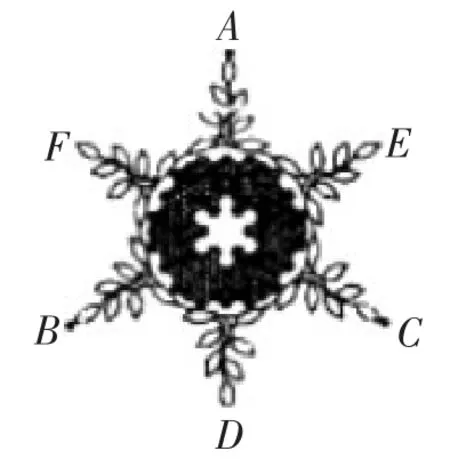
圖9

.

例13（四川·綿陽卷）在2022年北京冬奧會開幕式和閉幕式中，一片“雪花”的故事展現了“世界大同、天下一家”的主題，讓世界觀眾感受了中國人的浪漫.如圖10，將“雪花”圖案（邊長為4的正六邊形ABCDEF）放在平面直角坐標系中，若AB與x軸垂直，頂點A的坐標為A(2，-3).則頂點C的坐標為（ ）.

圖10

答案：A.

考查目標：例12和例13要求學生能運用銳角三角函數、勾股定理、正多邊形與圓、等邊三角形的性質和判定、坐標與圖形的相關知識解決實際問題.

命題意圖：兩道試題均以2022年北京冬奧會主火炬“雪花”圖案為現實情境，讓學生從中提取有效信息，構建數學模型.但兩道試題的考查角度略有不同.例12側重求正多邊形中相關角度的三角函數值，體現了設計圖案的特殊性.例13側重運用平面直角坐標系對“雪花”進行量化分析，體現了代數與幾何的統一性.雖然兩道試題的考查角度有所不同，但都充分挖掘了素材中蘊含的數學原理，考查了學生的數學抽象能力，強化了學生的數學應用意識.

命題評價：兩道試題的設計情境真實，符合實際，在考查相關知識技能的同時，突出了“數學來源于現實生活，又服務于現實生活”的理念，彰顯了數學的育人價值，體現了初中數學學習既要使學生有數學知識的增長，也要使學生有數學思維能力發展的課程目標和評價理念，引導教師在教學中應該揭示知識蘊含的數學本質及其體現的數學思想，幫助學生厘清相關知識之間的聯系和區別，發展數學核心素養.

例14（山東·濰坊卷）筒車（如圖11（a））是我國古代利用水力驅動的灌溉工具，車輪縛以竹簡，旋轉時低則舀水，高則瀉水.如圖11（b），水力驅動筒車按逆時針方向轉動，竹筒把水引至A處，水沿射線AD方向瀉至水渠DE，水渠DE所在直線與水面PQ平行；設筒車為⊙O，⊙O與直線PQ交于P，Q兩點，與直線DE交于B，C兩點，恰有AD2=BD·CD，連接AB，AC.

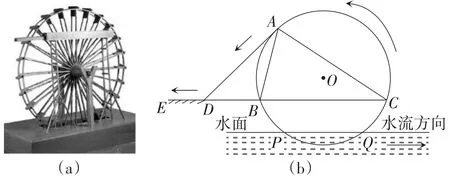
圖11

（1）求證：AD為⊙O的切線；

（2）筒車的半徑為3 m，AC=BC，∠C=30°.當水面上升，A，O，Q三點恰好共線時，求筒車在水面下的最大深度.（精確到0.1 m，參考值：.）

答案：（1）證明略.

（2）筒車在水面下的最大深度約為0.9 m.

考查目標：例14要求學生應用圓周角定理、切線的相關概念、相似三角形的性質與判定、解直角三角形等知識解決實際問題.

命題意圖：此題不再要求學生單純地在幾何圖形中解決求邊長的問題，而是通過數學問題的求解解決實際問題，引導學生運用數學的眼光觀察現實世界，運用數學的模型解釋生活實際問題.在用數學的方法解決實際問題的過程中，需要學生靈活運用所學知識分析問題.

命題評價：此題以我國古代利用水力驅動的灌溉工具——筒車為素材，讓學生體會古代勞動人民的智慧.通過數學抽象引導學生感受生活中蘊含著豐富的數學知識和物理知識.此題首先引導學生從實際問題中抽象出幾何圖形，需要學生具備遷移能力，并能夠將數學問題與實際問題建立關聯.第（1）小題考查切線的證明，區別于常規考法，將切線的實際意義蘊含其中；第（2）小題考查了角的數量關系運算，根據平行和垂直等位置關系，構造特殊三角形，利用銳角三角函數求出最大深度.此題將觀察、猜想、推理、計算融于一體，體現了“問題情境—建立模型—求解模型—解釋推斷”的數學建模過程.

4.體現應用，凸顯學科價值

2022年全國各地區中考數學試題選擇具有時代氣息的素材和具有優良數學文化底蘊的經典問題作為載體，關注數學與生活的聯系，進一步加強對學生數學應用意識的考查，提高學生對數學的整體認識和理解，體現了數學的應用價值，既有利于實現初中學業水平考試目標，較好地體現育人功能，也對初中數學教學起到了良好的導向作用.《標準（2022年版）》中指出，通過數學的眼光，可以從現實世界的客觀現象中發現數量關系與空間形式；應用意識主要是指有意識地利用數學的概念、原理和方法解釋現實世界中的現象與規律，解決現實世界中的問題；能夠感悟現實生活中蘊含著大量的與數量和圖形有關的問題，可以用數學的方法予以解決.應用型試題是指需要用數學的思想和方法來解決源于現實世界的、有實際背景的一類問題.此類試題有利于考查學生對相關知識和方法的理解水平，以及解決問題的意識與能力，有助于學生體會數學的應用價值和文化底蘊.

例15（浙江·金華卷）圖12是光伏發電場景，其示意圖如圖13所示，EF為吸熱塔，在地平線EG上的點B，B′處各安裝定日鏡（介紹見圖14）.繞各中心點（A，A′）旋轉鏡面，使過中心點的太陽光線經鏡面反射后到達吸熱器點F處.已知AB=A′B′=1 m，EB=8 m，，在點A觀測點F的仰角為45°.

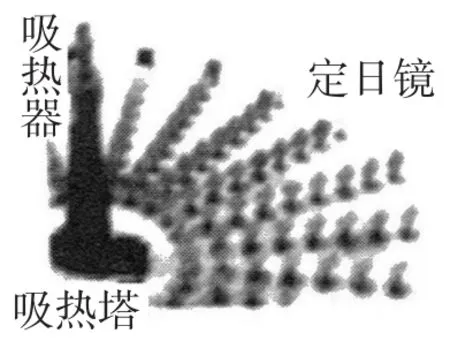
圖12

圖14

（1）點F的高度EF為_____.

（2）設∠DAB=α，∠D′A′B′=β，則α與β的數量關系是______.

答案：（1）9 m；（2）α-β=7.5°.

考查目標：例15要求學生能根據平行線的性質探究角的關系，根據三角函數值求角的度數，應用解直角三角形知識解決實際問題.

命題意圖：此題需要利用三角函數來解決實際問題，也是初中階段應用型問題考查的知識點之一.此題既是實際操作問題，也是三角函數題，又是幾何圖形題.雖然集多種功能于一身，但是考查難度較小，問題的設計充分體現出對數學應用意識的滲透.

命題評價：光伏發電場景體現了科技的發展，抽象出的數學模型簡單易懂，除考查數學知識外還考查了學生的數學閱讀能力，使學生更好地體會數學的應用價值和工具性作用，以及數學應用的廣泛性.

例16（北京卷）甲工廠將生產的Ⅰ號、Ⅱ號兩種產品共打包成5個不同的包裹，編號分別為A，B，C，D，E，每個包裹的重量及包裹中Ⅰ號、Ⅱ號產品的重量如表3所示.

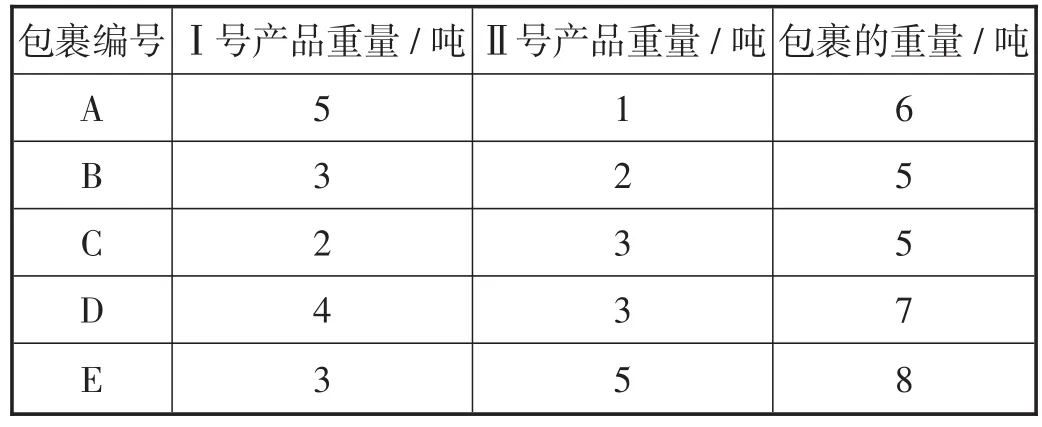
表3

甲工廠準備用一輛載重不超過19.5噸的貨車將部分包裹一次運送到乙工廠.

（1）如果裝運的Ⅰ號產品不少于9噸，且不多于11噸，寫出一種滿足條件的裝運方案_______（寫出要裝運包裹的編號）；

（2）如果裝運的Ⅰ號產品不少于9噸，且不多于11噸，同時裝運的Ⅱ號產品最多，寫出滿足條件的裝運方案_______（寫出要裝運包裹的編號）.

答案：（1）ABC（或ABE或AD或ACE或ACD或BCD）；（2）ACE.

考查目標：例16要求學生能夠運用方程、不等式等相關知識建立數學模型解決實際問題.

命題意圖：此題從具體的情境出發，考查學生的數學閱讀能力和邏輯推理能力，引導學生用數學的眼光發現問題，并將其轉化為數學問題，進而用數學的思維探索、分析和解決問題.

命題評價：此題的解決思路多樣，解決方法具有開放性，要求學生能選擇恰當的方法解決問題，既可以列舉出所有可能性，也可以借助方程或不等式討論量與量之間的關系，能對結果的實際意義做出解釋，有利于發展學生的數學應用意識，體現了數學在解決實際問題中的工具性作用.

5.關注思維，注重探究，體現學科素養

探究型試題是考查“數學思考”與“問題解決”課程目標落實情況的有效載體，需要學生對某一問題進行深入思考與研究，其解決過程沒有既定的公式或者解決途徑可以套用，要通過猜想或者證明的過程得到結果.《標準（2011年版）》指出，數學為人們提供了一種理解與解釋現實世界的思考方式.通過經歷獨立的數學思維過程，學生能夠理解、分析、解決簡單的數學問題和實際問題；能夠探究自然現象或現實情境所蘊含的數學規律，經歷數學“再發現”的過程；發展質疑問難的批判性思維，形成實事求是的科學態度，初步養成講道理、有條理的思維品質，逐步形成理性精神.而情境類試題中的探究性問題就需要學生通過數學思維，建立數學對象之間的邏輯聯系，并且運用符號運算、形式推理等數學方法，分析、解決數學問題或者實際問題.

關于“綜合與實踐”領域下的探究型問題，2022年全國各地區中考試卷中均有不同形式的體現，呈現方式有閱讀理解型問題、操作型問題、開放型問題等.此類問題有利于考查學生的數學探索能力，有利于評價學生的歸納、類比、概括、推理等思維能力水平.

例17（四川·樂山卷）華師版八年級下冊數學教材第121頁習題19.3第2小題及參考答案如下.

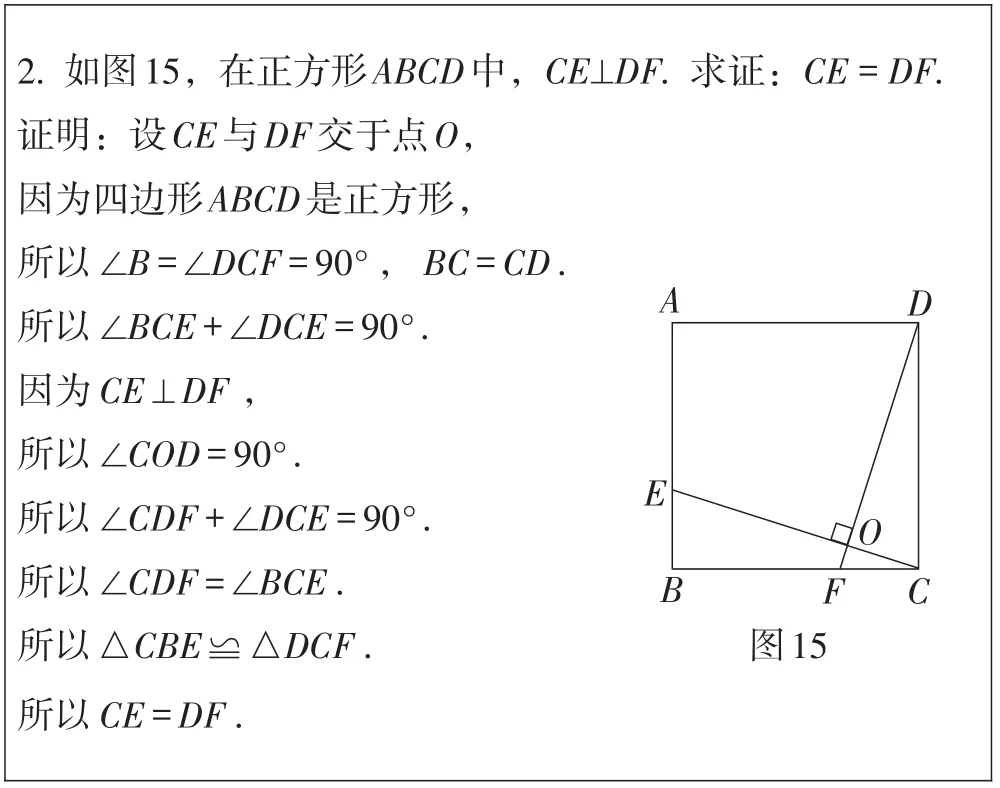
某數學興趣小組在完成了以上解答后，決定對該問題進一步探究.

（1）【問題探究】如圖16（a），在正方形ABCD中，點E，F，G，H分別在線段AB，BC，CD，DA上，且EG⊥FH.試猜想的值，并證明你的猜想.

（2）【知識遷移】如圖16（b），在矩形ABCD中，AB=m，BC=n，點E，F，G，H分別在線段AB，BC，CD，DA上，且EG⊥FH.則的值為_______.

（3）【拓展應用】如圖16（c），在四邊形ABCD中，∠DAB=90°，∠ABC=60°，AB=BC，點E，F分別在線段AB，AD上，且CE⊥BF.求的值.

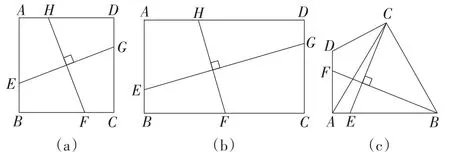
圖16

考查目標：例17要求學生運用全等三角形、相似三角形的性質和判定，以及四邊形和直角三角形的性質解決綜合問題.

命題意圖：此題是一道以四邊形為載體命制的綜合題，考查了旋轉的性質、平行四邊形的性質、矩形的性質、全等三角形的判定與性質、相似三角形的判定與性質、等邊三角形的判定與性質.

命題評價：此題以問題為導向，考查學生積累數學經驗、增強應用意識的能力.學生可以通過觀察、發現及證明，運用所學基礎知識和基本證明方法開展對圖形的探究.此題雖然難度較大，但是素材依舊來源于教材，引導教學重視教材、回歸教材.

2019年教育部發布的《關于加強初中學業水平考試命題工作的意見》中提出，各地要取消初中學業水平考試大綱，嚴格依據義務教育課程標準命題.從2022年全國各地區中考數學試題的命制中可以看出，命題的導向性還是十分明確的.一是盡可能挖掘教材中的素材，問題的設計更加基礎，突出對基礎知識、基本技能、核心概念的重點考查，提高了對課堂作為教學主陣地的重視程度；二是以科學和文化作為情境的試題重點考查學生運用數學知識解決問題的能力，充分挖掘數學學科的育人功能；三是關注探究和實踐過程，引導教學注重知識的形成過程和學生的學習過程，引導學生在學習中要能發現、會表達、肯探究，體會數學本質，體現數學核心素養的導向.

三、復習教學建議

1.學習課程標準，用好教材，立足課堂教學

綜觀2022年全國各地區中考數學試題，從命題的趨勢來看，引導教學重視課堂、重視教材，鼓勵教師挖掘教材中的素材，促進學生積極探究，重視知識的形成過程，讓學生經歷幾何圖形的觀察、構成要素關系的思考、有邏輯的數學表達、概括歸納、遷移運用等學習過程，體會數學是認識、理解、表達真實世界的工具、方法和語言，增強學生認識真實世界、解決現實問題的能力.因此，要求教師用好教材，不僅要關注教材中的定義、定理、例題、習題，更要關注引言、思考、探究、歸納、銜接性語言、小結反思等欄目，從教材中尋找數學知識再發現、再創造的途徑、過程和方法.教師只有充分理解教材，才能更好地用教材教學.

在課堂教學過程中，一方面，教師要以教材內容為教學載體，設計和選擇能夠引發學生思考的教學方式，注重采用啟發式、探究式、參與式、互動式等教學方式；另一方面，要強化情境的設計和問題的提出，注重發揮情境設計和問題提出對學生主動參與教學活動的促進作用，可以從社會生活、科學和學生已有的數學經驗等方面入手，圍繞教學任務，選擇貼近學生生活經驗、適合學生年齡特點和認知層次的素材，以體現數學學科的育人功能.

2.構建單元，形成結構，整體設計教學

《標準（2022年版）》中明確提出，要整體把握教學內容，注重教學內容的結構化，注重教學內容與核心素養的關聯，重視單元整體教學設計.

例如，在“數與代數”領域中，運算能力應該是貫穿于學習始終的，教師可以嘗試從明確運算對象、理解運算法則、求得運算結果、優化運算過程的角度，形成基于發展學生運算素養的單元教學設計；改變過于注重以課時為單位的教學設計，合理整合教學內容，分析主題—單元—課時的數學知識和核心素養的主要表現，確定單元教學目標，并落實到教學活動的各個環節中.

再如，在“圖形與幾何”領域中，知識內容比較多，要在有限的題量和考試時間內把學生對于幾何圖形的理解和學生學習過程的獲得考查出來，這就需要教師在復習過程中幫助學生從不同的角度和層次再次審視同一個知識點，通過形成知識結構，利用單元教學設計逐漸幫助學生站在較高的視角，完整地審視初中平面幾何圖形的性質，從而達到事半功倍的效果.在“圖形與幾何”領域，通過圖形的變化再次重構圖形的性質是學生需要具備的能力.因此，“圖形的變化”“圖形的性質”“圖形與坐標”三個專題實際上是緊密聯系的三個板塊.

在中考復習教學中，除了要加深學生對圖形的全面認識，更要使學生系統掌握教材知識，形成良好的數學認知結構.這是教師應做、能做且必須做好的工作.“系統掌握”是指學生頭腦中有清晰的、穩定的、可辨別的、遷移能力強的數學知識結構圖，不僅要理解知識及其中蘊含的數學思想方法，而且要明確知識之間的邏輯關系.復習課中，教師要讓學生在進一步明晰概念內涵的基礎上，把已學過的概念、定理、公式等用前后一致的數學思想串聯起來.這就必須讓學生重讀教材、梳理知識、形成專題、積累經驗，構建邏輯主線.從知識角度來講，“圖形的性質”專題主要涉及三角形、平行四邊形、圓等基本圖形；“圖形的變化”則包括平移、軸對稱、旋轉三種變化，考查的方式主要是借助直線型的基本圖形和圖形變化的性質來研究圖形構成要素之間的關系.復習的主要任務之一就是采用橫向聯系的方式，抓住運動變化的主線，突出知識之間的聯系，構建知識網絡，深化學生對知識的理解.

3.理解原理，提升思維，突出素養教學

數學的基本技能是能夠應用知識解決問題的載體.以實際問題為背景，開展學科綜合實踐活動或跨學科綜合實踐活動，能夠幫助學生將實際問題轉化為數學問題.從命題的角度來講，也需要學生經歷完整的探究過程，除了考查基本技能，還要考查其中蘊含的數學原理，要求學生理解數學本質.因此，在復習備考的過程中，要讓學生明確題目之間的聯系及其背后考查的數學原理，探求數學的本質.數學思想方法是對數學知識和方法形成的規律性的理性認識，是解決數學問題的根本策略，是溝通基礎知識與基本技能的橋梁，是數學知識的重要組成部分，是數學知識在更高層次上的抽象和概括，其蘊含在數學知識發生、發展和應用的過程中.因此，在復習時，教師要引導學生注意體會教材例題、習題及中考試題中所體現的數學思想和方法，培養學生用數學思想方法解決問題的意識.數學思想方法是數學的精髓，是讀書由厚到薄的升華.在復習過程中，教師要注重培養學生在解題中提煉數學思想的習慣，使學生能夠在活動中積累數學活動經驗，探索解決問題的基本思路和基本邏輯，在問題解決的過程中提升能力，發展數學核心素養.

總而言之，2022年全國各地區中考數學試卷都突出了“平穩”這一主題，適度創新，圍繞主干知識，注重對學生學習過程和學習方法的考查，凸顯素養導向，關注學生的持續發展.因此，在復習過程中，教師不僅要引導學生體會試題所蘊含的理念，關注知識的融合、結構的梳理，使之系統化、條理化，更要關注學生參與學習過程的完整性，幫助其形成數學思維，提高邏輯推理能力、數學閱讀能力，以及綜合運用數學知識分析問題、解決問題的能力，真正做到學懂數學知識、體會數學本質、感悟數學思想，學會并主動運用數學的思維創新解決問題.