高強度鋼方管局部感應加熱數值模擬及實驗研究

王 宇， 劉 靖， 馬曉燕， 韓靜濤,

(1. 北京科技大學 材料科學與工程學院，北京 100083；2. 欣諾冷彎型鋼產業研究院(曹妃甸)有限公司，河北 唐山 063200)

高強度鋼方管作為一種綠色環保的輕量化材料，通過減小自身截面尺寸和質量，降低焊接和涂裝工作量，減少能源和資源消耗，在汽車輕量化和鋼結構建筑等領域應用廣泛.然而，高強度鋼室溫下屈服強度高，在發生塑性變形時的流動應力、最小彎曲半徑和回彈量較大[1]，導致成形后的尺寸精度差[2]，且容易在彎角處出現裂紋[3].高強度鋼方管的主要塑性變形區域為圓角，在輥壓成形過程中存在厚度減薄缺陷和冷作硬化效應[4]，4個圓角的外形尺寸難以統一.為了避免出現角部裂紋，高強度鋼方管需要采用更大的圓角半徑，但會減小方管的應用范圍，同時增大焊接難度和工作量.

為了克服高強度鋼方管的冷成形難題，改善圓角區域的幾何尺寸和組織性能，彭雪鋒等[5]在冷輥壓成形工藝基礎上，提出局部熱輥壓成形工藝，在成形道次之前增添加熱裝置，對高強度鋼普通方管(下文中簡稱“方管”)進行二次輥壓成形，目的是將上述不均勻的4個圓角成形為圓角半徑極小的“尖角”，同時克服厚度減薄缺陷和冷作硬化效應.感應加熱技術具備加熱速度快、加熱效率高、環境污染小等優點，可以滿足局部熱輥壓成形工藝的技術要求.選用合適的感應加熱工藝參數，在圓角區域迅速獲得適宜溫度的透熱，是得到理想高強度鋼尖角方管(下文中簡稱“尖角方管”)的重要前提.

由于目前的測量手段難以獲得坯料表層以下的溫度分布，所以學者們對感應加熱技術中溫度場的研究多是借助有限元法.馬駿等[6]通過數值仿真，完成小型可變氣隙直流感應加熱器樣機的建模，探索不同加熱條件與鋁棒加熱分布間的關系.Guo等[7-8]分別建立圓管和方管的變曲率局部感應加熱彎曲成形工藝有限元模型，前者發現軸向推進速度和加熱工藝參數對成形結果影響顯著，后者研究了芯棒對成形質量和成形極限的影響.Wang等[9-11]分別將局部感應加熱技術應用到水火彎板和齒輪軋制工藝中，前者通過熱彈塑性分析，研究了不同工藝參數對鋼板彎曲結果的影響，后者通過分析溫度場結果，對加熱線圈的結構進行了優化，同時減輕成形缺陷，提高了成形精度.此外，研究表明，在加熱線圈上安裝導磁體可以增強局部感應加熱效果[12]，不同幾何尺寸的導磁體對加熱速率和溫度分布均勻性也有顯著影響[13].

盡管不少學者已經對感應加熱技術進行了數值模擬研究，但絕大多數研究重點僅為溫度場，而電磁場作為影響溫度場的根本源頭，相關研究很少.與此同時，很多數值模擬研究缺乏相應實驗驗證，而測溫槍作為目前最常用的測溫儀器，只能進行單點溫度捕捉且準確度不高.彭雪鋒等[5]選用700 ℃作為最高熱成形溫度，成形后的方管外圓角半徑為2 mm，約等于板帶厚度，但是內圓角處萌發了大量微小裂紋，在后續工程應用中存在安全隱患，這表明加熱工藝參數有待進一步優化，否則無法徹底解決高強度鋼成形難題.

為了進一步提升高強度鋼方管“尖角化”效果，即大幅減小外圓角半徑并消除裂紋缺陷，同時避免傳統“試錯法”造成的資源浪費，本文建立局部感應加熱輥壓成形工藝的電磁-溫度場耦合模型，從電磁場角度揭示溫度場變化的根本原因，對加熱工藝參數進行系統性優化.采用數值模擬優化后的加熱工藝參數開展實驗研究，并利用紅外熱像儀對整個加熱區域進行高精度的溫度捕捉，驗證有限元模型的預測精度.

1 數學模型

1.1 電磁場模型

局部感應加熱輥壓成形工藝中，方管加熱的基本電磁場理論是麥克斯韋方程組，它由4個方程組成，微分形式如下[14]：

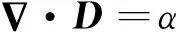
(1)

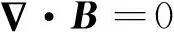
(2)

(3)

(4)

式中：D為電位移矢量；α為電荷密度；B為磁感應強度矢量；E為電場強度矢量；H為磁場強度矢量；J為電流密度矢量；t為時間.

假設分析域內不存在自由載荷，則式(1)和(4)可以簡化為

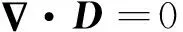
(5)

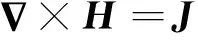
(6)

在電磁場分析中，直接求解E和H并不方便，為了降低求解難度，引入矢量磁位A和標量電位φ，分別滿足：

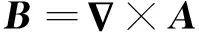
(7)

(8)

此外，B、H、J、E之間還滿足以下關系：

J=Je+Js=σE+Js

(9)

B=μH=μ0μrH

(10)

式中：Je為感應電流密度；Js為激勵源電流密度；σ為電導率；μ為磁導率；μ0為真空磁導率；μr為相對磁導率.

假設源電流隨時間按正弦規律變化，將式(7)～(10)代入式(6)，整理得到電磁場的控制方程：

(11)

1.2 溫度場模型

方管溫度場的變化遵循熱力學第一定律，熱傳導過程遵循傅里葉定律[14]：

(12)

式中：ρ為密度；c為比熱容；T為溫度；k為導熱系數；Q為加熱功率密度.

將Je和σ代入得：

(13)

同時考慮熱對流和熱輻射兩種傳熱方式，方管內外表面溫度邊界條件如下所示：

(14)

式中：n為邊界面法向量；h為表面對流換熱系數；Tamb為環境溫度；ε為表面發射率；σsb為斯特藩-玻爾茲曼常量.

2 幾何模型及邊界條件

方管局部感應加熱的三維模型如圖1(a)所示.方管的圓角外側排布著平行于z軸方向的同一根銅管，銅管外側安裝有導磁體.為了保證加熱段銅管的平行度，銅管兩端分別加裝固定板.銅管、導磁體和固定板一同構成加熱線圈的主體.

為了提高求解效率，對三維模型進行簡化，將圖1(a)中所標橫截面的二維模型作為研究對象建模，將方管形心設為平面直角坐標系的原點，如圖1(b)所示.

為了更加貼近實際狀況下的磁感線分布狀態，在模型的最外圍邊界上施加磁感線平行邊界條件：

A=0

(15)

電磁場在其他內部邊界上具有連續性，渦流區和非渦流區交界面的邊界條件[15]為

n×(H1-H2)=0

(16)

式中：H1和H2分別為渦流區和非渦流區的磁場強度矢量.

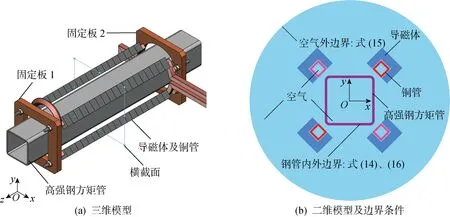
圖1 幾何模型Fig.1 Geometric model

3 數值模擬

數值模擬過程可分為3個部分：前處理、求解以及后處理.本文基于ANSYS參數化設計語言(ANSYS Parametric Design Language, APDL)，實現了全流程的參數化設計與分析.

3.1 前處理

首先在繪圖軟件中繪制二維模型，導出為通用圖形文件，然后導入到ANSYS中生成幾何模型.之后，定義單元類型和材料參數并指定給相應幾何面，設置網格密度并完成網格劃分，如圖2所示.可以看出，空氣域的網格形狀不規則且尺寸最大.方管、銅管和導磁體的網格均由規則四邊形構成，且網格細小，過渡均勻.從內圓角到外圓角，方管網格的徑向厚度逐漸減小，外圓角表層的網格厚度最小，設為室溫下集膚深度的一半，這樣可以充分模擬出感應加熱的集膚效應.最后選擇相應邊界，分別施加電磁場和溫度場邊界條件.前處理中所有點、線和面的選擇以及數值設定都基于APDL命令流，這樣可以大幅降低改變幾何模型或者載荷參數后的工作量.

為保證計算結果準確性，所有物理量都采用國際單位制.方管橫截面寬度和高度均為0.04 m，厚度為0.002 m，內、外圓角半徑分別為0.002 m和0.004 m.在電磁場分析中，銅管、方管、導磁體和空氣域均選用基于矢量磁位理論的二維八節點磁單元PLANE53.而在溫度場分析中，由于只研究方管的溫度變化，所以只需將方管單元定義為二維八節點熱單元PLANE77，其他區域無需定義熱單元.

定義銅管、空氣域和導磁體的相對磁導率μr分別為1、1及 1 000，由于三者不參與溫度場計算，所以無需額外定義溫度場相關的材料參數.方管參與電磁場和溫度場的耦合計算，需要定義隨溫度變化的相對磁導率μr、電阻率ρT、導熱系數k和比熱容c等材料參數[16]，如表1所示.

前處理主要常數如表2所示，其中環境溫度Tamb設為室溫293 K.方管表面與周圍空氣的對流換熱系數h[17]選用40 W·m-2·K-1.于坤等[18]的研究成果表明，當溫度超過900 ℃以后，ε趨于0.7，所以本文選用ε為0.68.

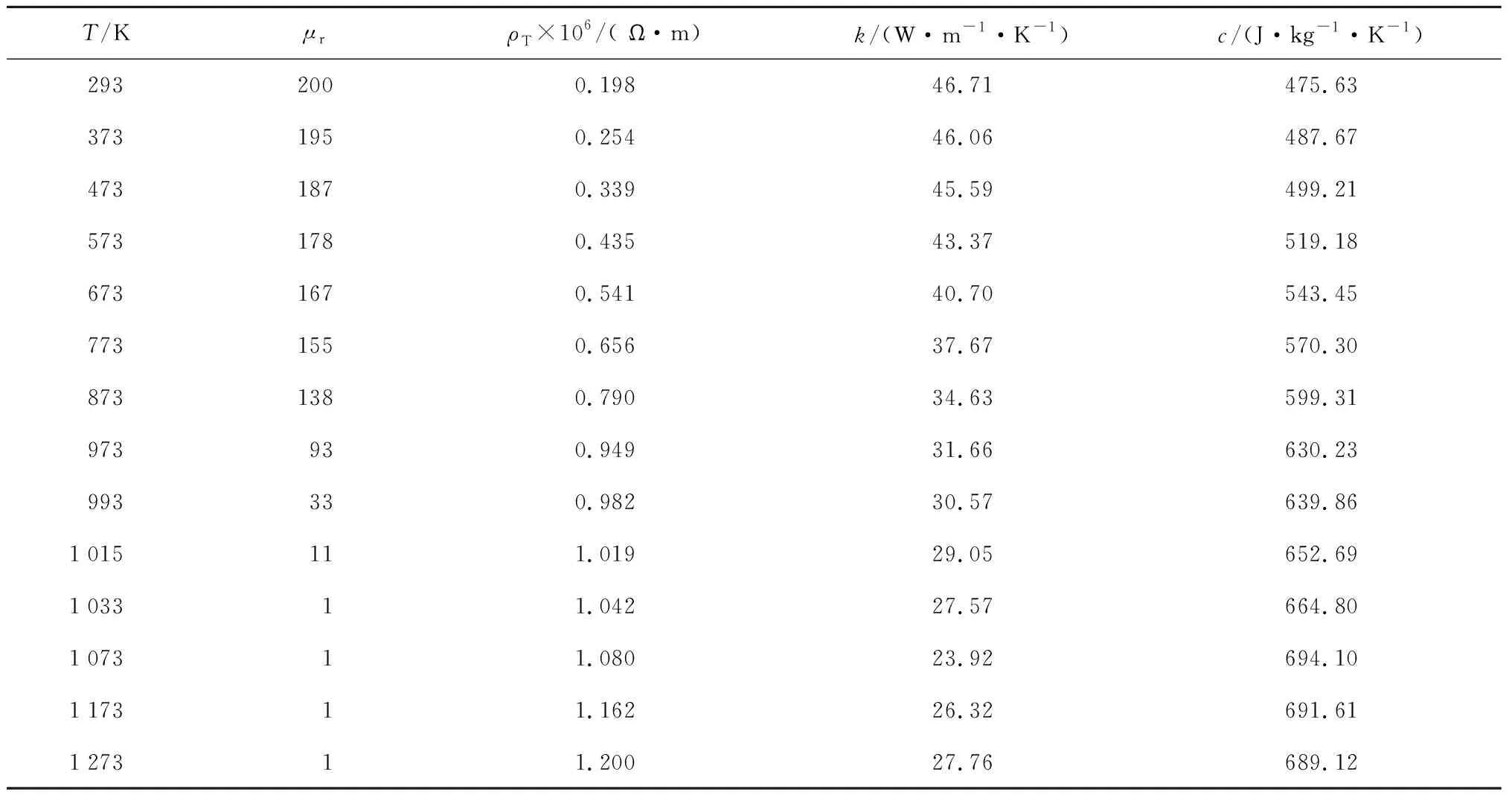
表1 高強度鋼材料參數Tab.1 Material parameters of high strength steel

3.2 求解流程

感應加熱技術是一種建立在電磁感應和電流熱效應兩個物理原理基礎上的電加熱方法，因此感應加熱數值模擬涉及到電磁場和溫度場的耦合分析，本文選用物理環境法實現它們的順序耦合.此方法使用同一個滿足所有物理場要求的實體模型和網格，然后創建多個用來定義物理環境的物理文件，基于APDL命令流，反復調用不同文件，實現載荷在多物理場中的傳遞，計算流程如圖3所示.其中，Δt為時間步增量，n為預設步數.

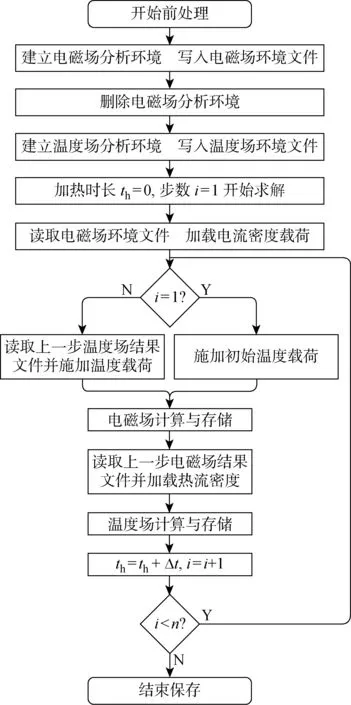
圖3 電磁-溫度順序耦合計算流程Fig.3 Electromagnetic-temperature sequential coupling calculation process

首先分別在電磁場和溫度場環境中完成相應的設置，并寫入到不同的物理環境文件中.下一步基于APDL命令流，先調用電磁場環境文件，施加初始溫度載荷，完成第一次電磁場的求解，保存結果到電磁場結果文件中.之后讀取該結果文件，將感應電流生成的焦耳熱作為內熱源加載到溫度場中，完成溫度場的求解并保存，根據求解后的實時溫度，對材料參數進行更新.最后根據時間步增量Δt更新加熱時長th，同時分析步數i增加，進入下一個分析步的求解.整個過程循環往復，直到分析步數i增加到與預設步數n相等時，循環結束，求解完畢.

3.3 模擬參數

在局部感應加熱過程中，銅管和方管之間的加熱間距、銅管橫截面尺寸及長度、導磁體的選用、加熱頻率、加熱功率及加熱時長是7個主要的模擬參數.理論上，銅管和方管之間的加熱間距越小，加熱效率越高，但是兩者也更容易接觸，造成短路.綜合考慮加熱效率和安全性，銅管外表面和方管外圓角最短距離定為0.004 m.根據方管圓角區域的幾何尺寸和加熱間距，選用的銅管橫截面寬度和高度均為0.01 m，厚度為 0.001 5 m.銅管長度較短時，對加熱功率的要求較大，會造成不必要的設備成本增加，而銅管過長時，由于銅管自重及加工制作難度，銅管的平面度和平行度會有所下降，綜合考量后，加熱段銅管長度選用0.1 m.

除了上述3個標量參數，將剩余4個參數作為變量參數考慮，為了研究導磁體的影響，分別建立含導磁體模型和無導磁體模型，考慮到實際黏結狀態，將導磁體與銅管的間隙值設為 0.000 5 m.根據方管厚度值0.002 m和加熱溫度峰值 1 100 ℃，加熱頻率范圍選取1～100 kHz，加熱功率范圍選用 30～55 kW.通過加熱功率換算得到電流值，再將電流值除以銅管截面積，得到加載在銅管上的電流密度.考慮到實際電流的走向與圖1(a)中的z軸平行，規定一、三象限銅管上的電流密度為正值，二、四象限銅管上的電流密度為負值，由于整個電路串聯，所以各象限電流密度的絕對值相等.加熱時長為加熱段銅管長度和方管移動速度之比，由于加熱段銅管長度已定為0.1 m，所以當方管移動速度范圍選用0.5～6 m·min-1時，相應得到加熱時長的范圍為1～12 s.

將有限元模型求解之后的結果分別存儲在電磁場結果文件和溫度場結果文件中，分別讀入兩個文件，從某一時刻云圖結果、隨路徑或時間變化的節點結果等方面進行討論與分析.

4 結果與討論

4.1 導磁體的效果

加熱頻率為80 kHz，加熱功率為30 kW，加熱時長為1 s時的磁感線分布如圖4所示，其中圖4(a)和圖4(b)分別為無導磁體模型和含導磁體模型的整體結果圖以及第一象限結果圖.由圖4(a)可以看出，在銅管外表面區域，磁感線最為密集，而距離銅管中心越遠，磁感線越稀疏.但由于方管的存在，原本呈圓形分布的磁感線被迫經過外圓角表層，從而增大了表面磁感線密度.由圖4(b)可以看出，在導磁體的作用下，磁感線分布區域大幅縮小，尤其是在導磁體外側空氣域中，幾乎不存在磁感線.與此同時，由于大量磁感線從導磁體內穿過，所以方管外圓角表層的磁感線密度大幅上升.

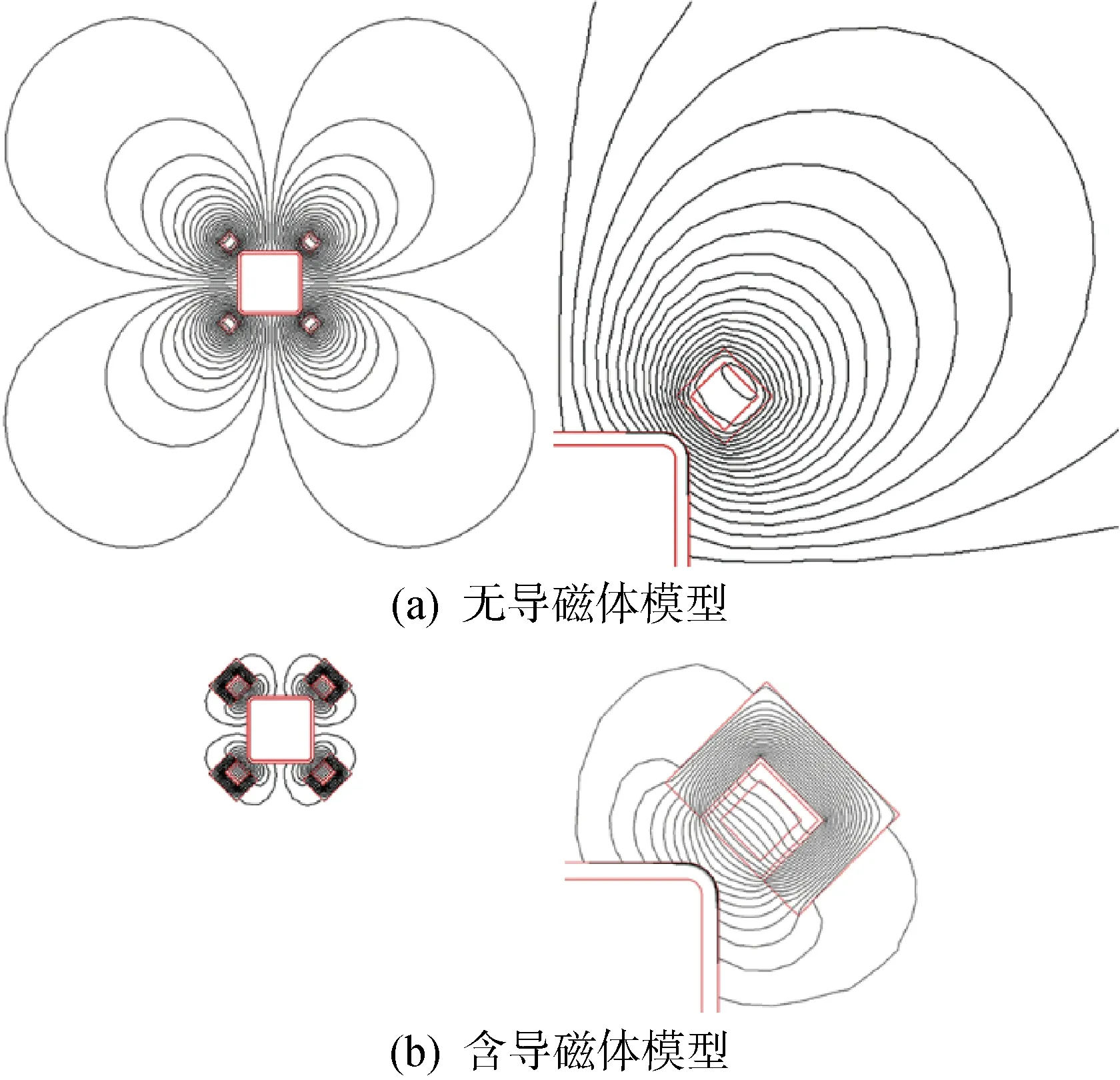
圖4 導磁體對磁感線的影響Fig.4 Influence of magnetizers on magnetic induction line

導磁體的相對磁導率遠高于空氣、銅管和方管，強烈降低了所處區域的磁阻，可以將原本自由散布在空氣域中的磁感線“吸引”到體內，使磁感線從體內穿過，大幅提升體內磁通量，然后通過控制開口位置，將體內高密度磁感線引導至待加熱區域.在其他模擬參數相同的情況下，可以明顯看出導磁體對空間磁感線分布的控制能力以及對局部區域磁通量的大幅提升效果.

與圖4相同的加熱參數下的磁場強度(H)結果如圖5所示.由圖5(a)可以看出，與磁感線分布規律相同，磁場強度在與方管圓角相鄰的銅管外壁附近達到了最大值，約為 27 990 A/m，磁場強度沿銅管外表面向外逐漸遞減.而在圖5(b)中，磁場強度最大值出現在相似位置，約為 239 700 A/m，大于圖5(a)中磁場強度極值的8.5倍.可以看出，在導磁體開口位置與方管圓角之間，營造出了強磁場區域，而在導磁體的另外3個方向，磁場強度迅速衰減，接近0.

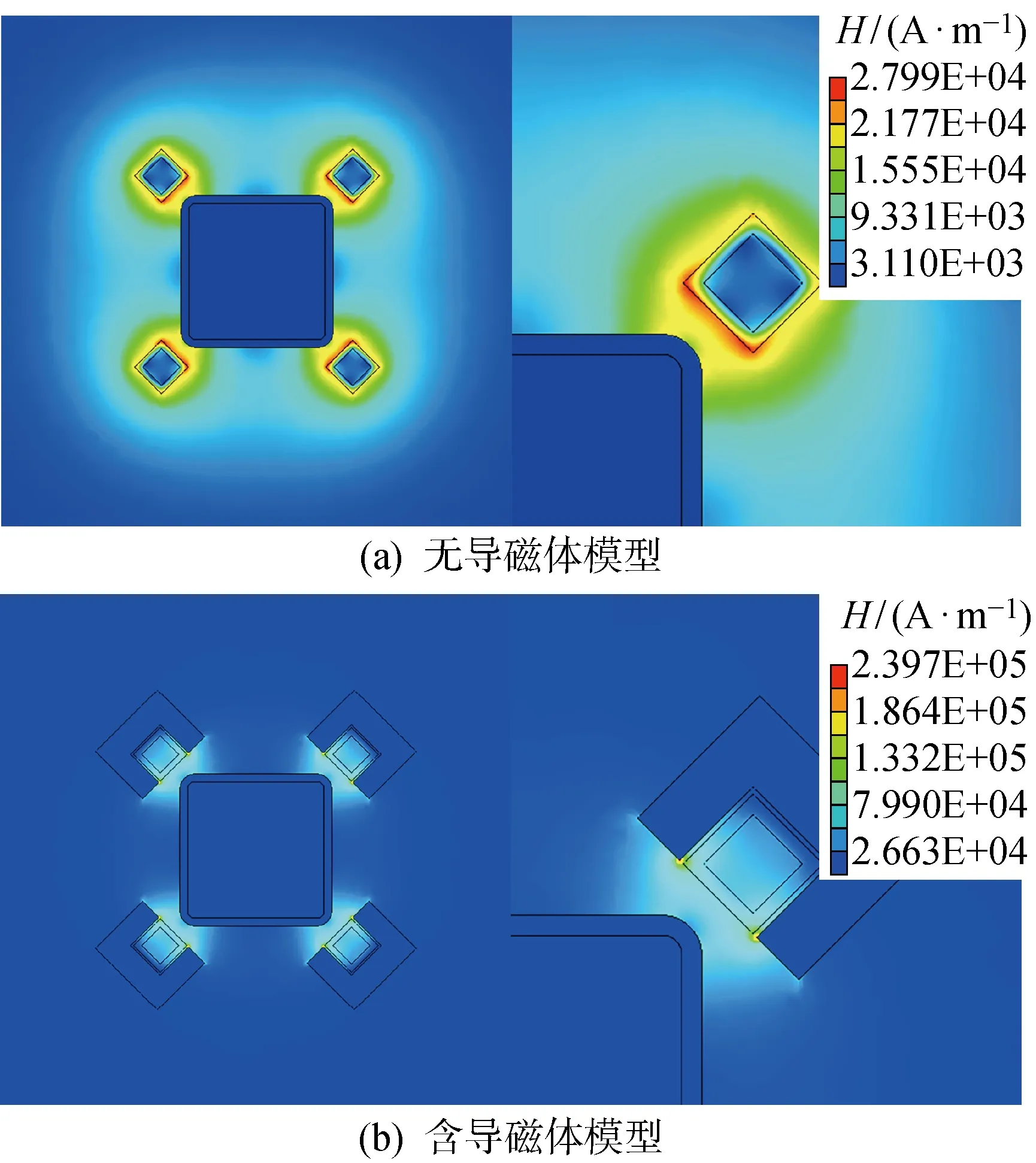
圖5 導磁體對磁場強度的影響Fig.5 Influence of magnetizers on magnetic field intensity

無導磁體模型的加熱溫度峰值僅為91.7 ℃，而含導磁體模型則達到了350.2 ℃，約是前者的4倍.導磁體將原本發散的磁場集中到方管外圓角區域，使該區域的磁場強度提高近一個量級，這是導磁體能夠大幅提升加熱效率的根本原因.

4.2 加熱頻率的影響

為研究加熱頻率(f)對模擬結果的影響，采用含導磁體模型，選用物理環境法，加熱時長選用1 s，加熱功率選用P=30 kW，對f=1，80 kHz 分別建模分析.圖6所示為兩種加熱頻率下圓角區域加熱溫度和磁感應強度(B)分布情況.可以看出，當f=1 kHz時，圖6(a)中方管圓角溫度分布較為均勻，最大值位于外圓角表層中心，約為20.23 ℃，相比較環境溫度20 ℃，升溫幅度極小.當f=80 kHz時，圖6(b)中溫度最大值仍在同一位置，約為 354.6 ℃，但無論是徑向還是周向，溫度差值都明顯增大，內外圓角中心位置溫差約為100 ℃.

圖6 加熱頻率對加熱溫度和磁感應強度的影響Fig.6 Influence of heating frequency on heating temperature and magnetic flux density

由式(13)可知，感應電流密度Je直接決定加熱功率密度Q的值，而感應電流密度Je的值和分布規律又與磁感應強度B保持一致.當f=1 kHz時，如圖6(c)所示，方管圓角區域的磁感應強度分布范圍較廣，覆蓋了從外圓角表層到約1/2板厚的區域，表層磁感應強度最大，約為1.543 T.當f=80 kHz 時，圖6(d)中方管圓角區域的磁感應強度分布范圍很窄，集中在從外圓角表層到約1/10板厚的區域，與此同時，表層磁感應強度峰值約為5.861 T.通過對比可知，當f從 1 kHz 提升到 80 kHz 時，磁感應強度覆蓋區域減少了80%，表層磁感應強度提升到近4倍，這使得表層溫度提升了約16倍.

當加熱頻率較低時，磁感應強度在較大區域內均勻分布，整個區域緩慢升溫，而當加熱頻率增加后，磁感應強度大幅提高并集中在外圓角表層區域，加熱速度和溫度大幅提升，但同時會增大外圓角和內圓角之間的溫差.由此可見，存在最佳加熱頻率，可以在適當的加熱速度下，實現圓角區域均勻透熱的加熱要求.

為了找到最佳加熱頻率，在其他參數不變的情況下，額外進行20、40及60 kHz共3種加熱頻率下的數值模擬，從外圓角中心點到內圓角中心點路徑的磁感應強度分布如圖7所示，圖中d為外圓角中心點沿徑向的深度.可以看出，不同頻率下的磁感應強度都呈現出先增長至峰值，再衰減至0的趨勢.磁感應強度峰值與加熱頻率成正比，而峰值所處深度以及歸零深度則與加熱頻率成反比.f=1 kHz時，磁感應強度峰值在約0.15 mm深度出現，并且在約 1.2 mm 深度(1/2板厚附近)趨于0，這與圖6(c)的結果完全吻合.對于其他4種加熱頻率，峰值所處深度均小于0.04 mm，磁感應強度在0.3 mm深度之內基本都已歸零.

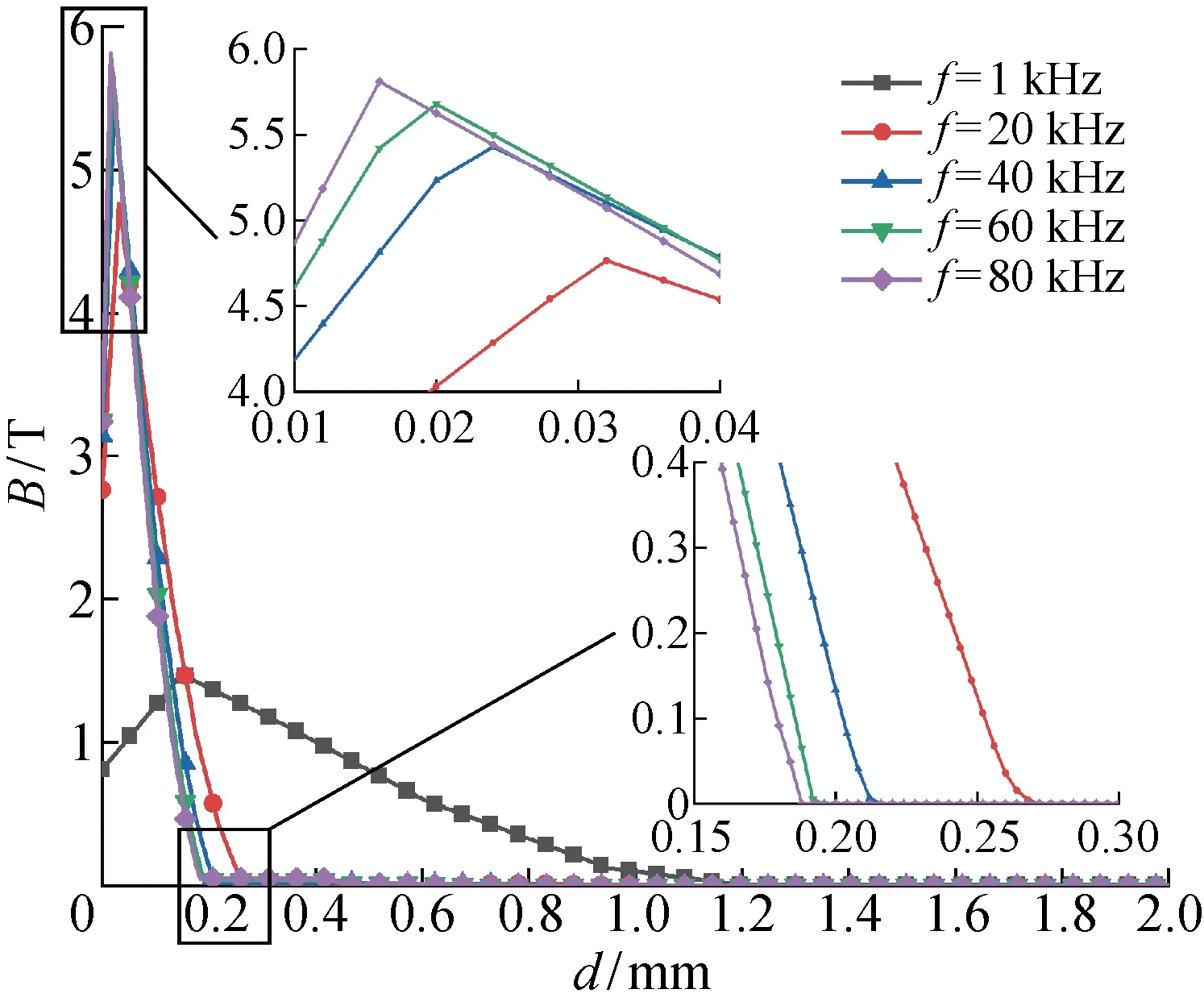
圖7 磁感應強度隨加熱頻率的變化Fig.7 Magnetic flux density versus heating frequency

圖6和7表明，隨著加熱頻率提升，磁感應強度峰值所處深度和歸零深度均向外圓角表層移動.當加熱頻率較高時，磁感應強度在距離表層不到1/10厚度的區域內，迅速增長至峰值并急速衰減至0，表明磁感應強度具有與感應電流相似的集膚效應.這決定了工件表層最先被加熱，直到表層溫度超過居里點后，表層失磁，加熱位置才開始向深層移動，導致表層和深層之間存在從高溫到低溫的溫度梯度.圓角區域均勻透熱的實質是要保證內圓角區域達到目標加熱溫度的同時，盡量縮小外圓角表層峰值溫度與目標加熱溫度的溫度差值.

高強度鋼方管材質為亞共析鋼，通過JMatPro軟件計算得到，在平衡狀態下的奧氏體和鐵素體共存的最高溫度約為840 ℃，考慮到感應加熱過程溫升速度較快，所以把目標加熱溫度提高至900 ℃，讓鐵素體盡可能多地轉變為奧氏體.為了滿足厚度方向均勻透熱的加熱要求，當加熱功率為50 kW，內圓角中心位置達到900 ℃時，對不同加熱頻率所需加熱時長以及外圓角和內圓角中心位置的溫度差值(ΔT)進行統計，計算相鄰兩數據點之間的增長率，結果如圖8所示.

圖8 加熱時長和溫度差值隨加熱頻率的變化Fig.8 Heating time and temperature difference versus heating frequency

從圖中可以看出，隨著加熱頻率的增加，加熱時長逐步降低，溫度差值不斷增大.當f從20 kHz增加到40 kHz時，加熱時長減少了68%，溫度差值增加了150%，而當f超過40 kHz以后，加熱時長的降低率和溫度差值的增長率都逐步減小.這是因為圓角區域幾何尺寸和材料性能參數的限制，當f超過40 kHz以后，不管是磁感應強度峰值、峰值出現位置還是歸零位置，差距都明顯縮小(見圖7).

當f=40 kHz，P=50 kW時，內圓角中心在t>2.6 s后到達900 ℃，此時內外圓角溫度差值約為66 ℃.不足3 s的加熱時長和小于70 ℃的溫度差值可以滿足加熱要求，而當加熱頻率進一步增加時，加熱時長下降的優勢已經無法彌補設備成本以及溫度差值提升帶來的劣勢.綜上所述，最佳加熱頻率選取為40 kHz，同時為了方便計算，將加熱時長 2.6 s 取整為3 s，對應的鋼管移動速度為2 m/min.

4.3 加熱功率的影響

在圖8結果基礎上，選定加熱頻率及時長分別為40 kHz及3 s，對47.5、50.0、52.5及55.0 kW共4種加熱功率下的電磁-溫度場進行數值模擬，將溫度大于等于900 ℃的區域著色顯示，結果如圖9所示.可以看出，當其他參數相同時，加熱功率越大，高溫區域和溫度峰值也越大.

當加熱功率為47.5和50.0 kW時，如圖9(a)和9(b)所示，只有部分圓角區域溫度達到了 900 ℃ 以上.當加熱功率為52.5 kW時，如圖9(c)所示，整個圓角區域溫度剛好達到900 ℃以上，溫度峰值約為 1 117 ℃，加熱效果比較理想.而當加熱功率提升到55.0 kW時，如圖9(d)所示，900 ℃以上的溫度區域遠超圓角區域，此時的溫度峰值位于外圓角中心，約為 1 197 ℃，外圓角區域容易出現組織過熱，甚至有過燒和熔化的風險.綜上所述，加熱功率應優先選用52.5 kW.

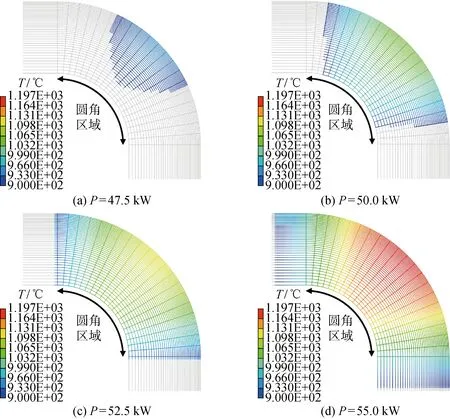
圖9 圓角區域溫度分布隨加熱功率的變化Fig.9 Temperature distribution at fillet area versus heating power

5 實驗研究

5.1 加熱溫度

為了驗證數值模擬結果的準確性，按照圖1幾何模型制作加熱線圈，使用和有限元模型相同的標量參數以及優化后的變量參數，開展高強度鋼方管局部感應加熱輥壓成形實驗研究.其中，優化后的變量參數如下：在銅管外安裝相同尺寸的導磁體；選用加熱頻率為40 kHz、最大輸出功率為120 kW的超音頻感應加熱設備；鋼管移動速度為2 m/min，對應加熱時長為3 s；加熱功率優選52.5 kW，另外兩組對照實驗的加熱功率分別為42.5和47.5 kW.實驗過程中，借助紅外熱像儀測量方管外表面加熱溫度，熱像儀與方管之間的測量距離約為0.5 m.

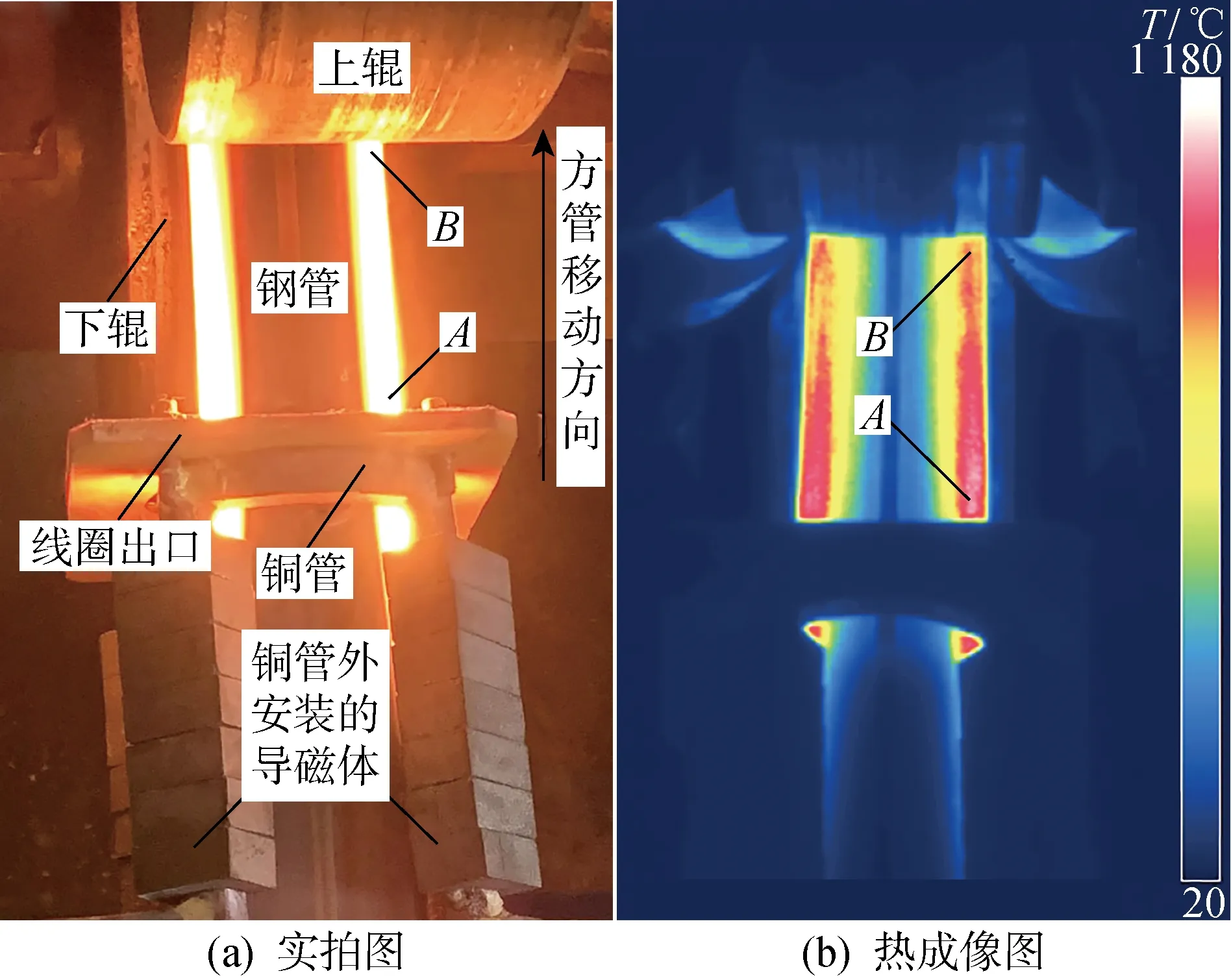
圖10 局部感應加熱實驗Fig.10 Local induction heating experiment

當加熱功率為52.5 kW時，局部感應加熱實驗的實拍圖和熱成像圖如圖10所示.方管自下而上移動，穿過線圈之后，進入成形道次.由于銅管和導磁體的遮擋，無法直接測量加熱段的溫度分布，只能通過測量空冷段的溫度分布，驗證數值模擬結果的準確度.在專業后處理軟件中，選用與表2中一致的發射率，提取右側外圓角中心從剛離開線圈到即將進入成形道次之間(A點與B點之間區域)的溫度分布曲線.

基于APDL命令流，采用含導磁體模型和物理環境法，f=40 kHz，進行P=42.5，47.5，52.5 kW的局部感應加熱數值模擬.根據方管移動距離和速度之比，得到分析時長為4.5 s，其中加熱時長為3 s(從進入到離開線圈所需時間)，空冷時長為1.5 s，略大于從A點移動到B點所需時間.提取第一象限外圓角中心溫度隨時間變化的曲線，結合方管移動速度，將時間換算成實際位移，即可獲得方管外圓角中心溫度在加熱段和空冷段的變化曲線.

熱像儀測溫結果和數值模擬結果如圖11所示，其中D為電位移.在加熱段初期，即加熱溫度低于居里點(約770 ℃)之前，溫升速度較快，且與加熱功率成正比.當加熱溫度達到居里點附近時，由于方管的相對磁導率、比熱容及熱導率發生劇烈變化，致使溫升速度陡然上升.當加熱溫度超過約900 ℃后，由于方管外圓角早已失磁，此時溫度上升的熱量來源為深層加熱位置的熱傳導，所以溫升速度大幅下降.在空冷段，方管外圓角的熱傳遞方式主要為與空氣的熱輻射和熱對流以及與圓角深層位置的熱傳導，溫降速度與幅度均與加熱功率成正比.

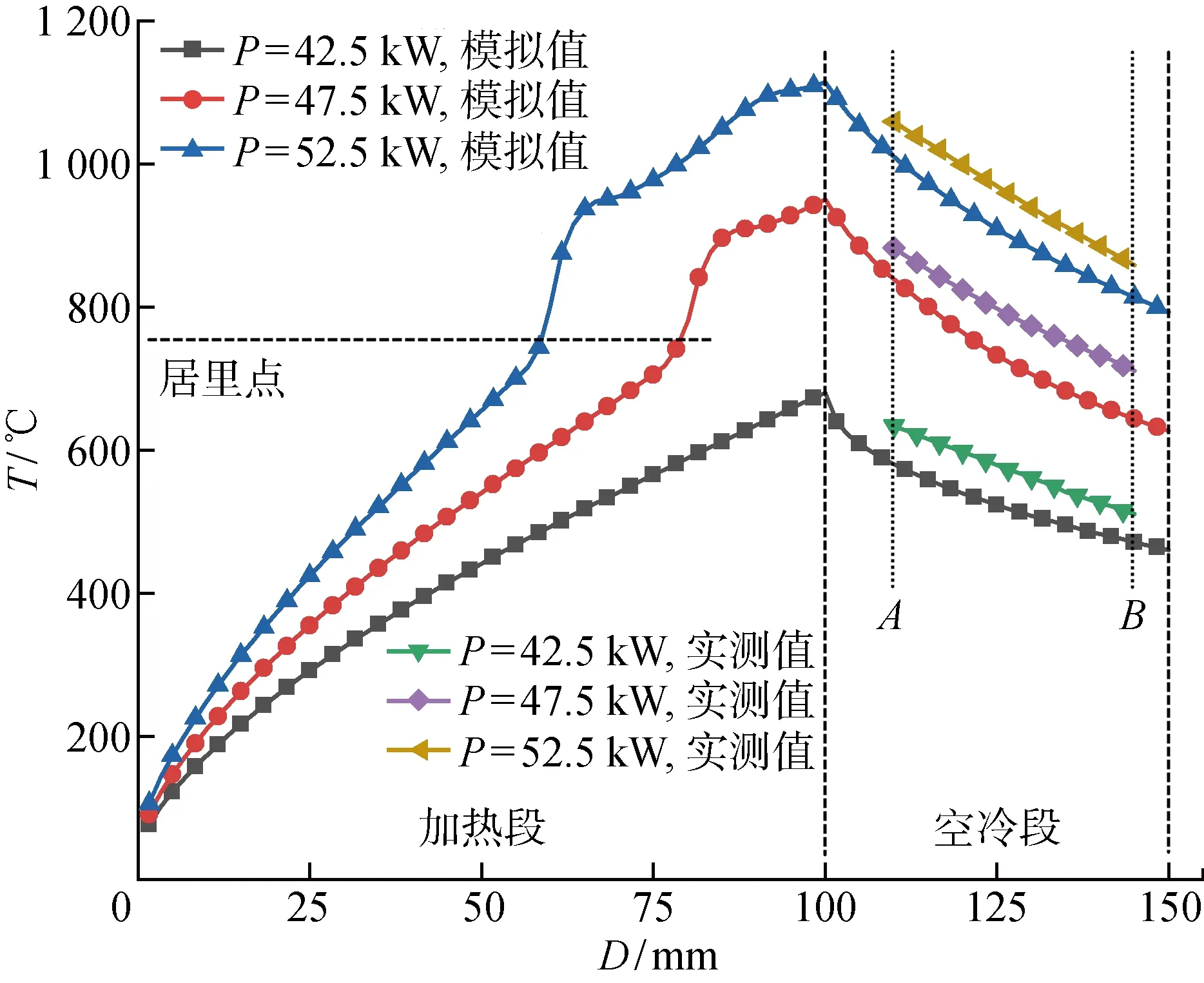
圖11 溫度實測值與模擬值的對比Fig.11 Comparison of measured and simulated temperature

在3種加熱功率下，A點和B點之間的加熱溫度模擬值均低于實測值.然而根據實測值曲線的變化不難發現，在加熱段和空冷段的分界處，即D為100 mm時，實測值與模擬值的準確度有所提升.這是因為方管外圓角在空冷段，只有熱量的流失，材料熱物性參數的取值對溫度變化起到決定性作用，比如模型中采用恒定的表面換熱系數，而實際狀況下，它應當跟隨溫度差值的變化而改變.

當加熱功率為42.5、47.5 及52.5 kW時，20個數據點的誤差均值分別為8.95%、8.02%及5.74%，說明方管的材料熱物性參數更加適用于高溫場合.3種加熱功率下，溫度模擬值與實測值的誤差均值約為7.57%，說明有限元模型具備一定的預測能力，與實際情況吻合良好.

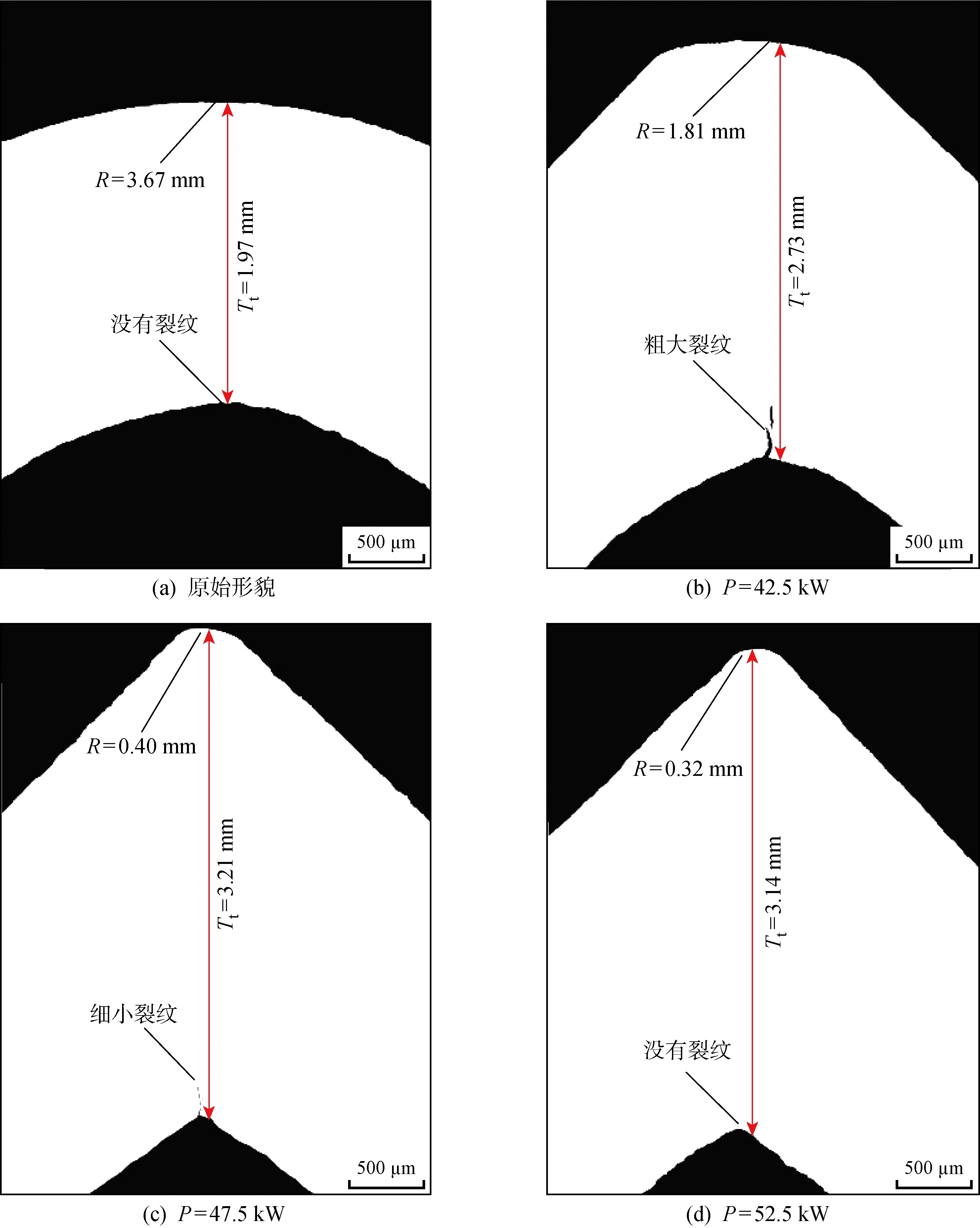
圖12 角部區域形貌隨加熱功率的變化Fig.12 Morphology at fillet area versus heating power

5.2 角部區域形貌

對普通方管和3種加熱功率下成形后的尖角方管角部區域分別取樣，經過鑲嵌—粗磨—細磨—拋光后，在金相顯微鏡下觀察形貌，如圖12所示.其中圖12(a)為普通方管的原始角部區域形貌，圖12(b)～12(d)分別為P=42.5，47.5，52.5 kW成形后的尖角方管角部區域形貌.如圖12(a)所示，普通方管的角部區域厚度Tt最小，為1.97 mm，外圓角半徑R最大，為3.67 mm，整個區域沒有裂紋.當P=42.5 kW時，如圖12(b)所示，R值減小到 1.81 mm，Tt增加到2.73 mm，但是內圓角位置出現了0.34 mm長的粗大裂紋.當P=47.5 kW時，如圖12(c)所示，R減小到0.40 mm，Tt增加到 3.21 mm，但是內圓角位置仍有0.18 mm長的細小裂紋.當P=52.5 kW時，如圖12(d)所示，R繼續減小到0.32 mm，Tt為3.14 mm，未出現任何裂紋.

普通方管角部區域經過多道次冷彎成形，從平直板帶逐漸彎曲成圓角，不可避免地出現彎曲減薄現象，相比較板帶厚度2 mm，角部厚度降低了 0.03 mm，此時R超過板厚的1.8倍，足夠大的彎曲半徑確保角部區域未出現裂紋.然而，當P=42.5 kW 時，圓角形貌開始發生較大變化，Tt超過板厚，R小于板厚，但是由于加熱功率不足，導致內圓角區域溫度較低，成形時出現了粗大裂紋.

當P提升到47.5及52.5 kW時，Tt和R分別進一步增加和減小.參照圖9(a)和圖9(c)所示，當P=47.5 kW時，內圓角區域溫度仍低于 900 ℃，導致成形時出現細小裂紋，而當P=52.5 kW 時，由于整個圓角區域溫度均超過 900 ℃，充分提升了高強度鋼塑性變形能力，與原始形貌相比，Tt增加約59%，R減小約91%；與文獻[5]研究結果相比，R減小約84%，同時徹底克服內圓角裂紋缺陷，消除后續使用中的安全隱患.

6 結論

(1) 基于矢量磁位法和物理環境法，利用APDL命令流建立局部感應加熱輥壓成形工藝的電磁-溫度場耦合模型.分析不同加熱工藝參數對模擬結果的影響，并基于優化后參數進行實驗研究.加熱溫度模擬值與實測值的誤差均值約為7.57%，說明有限元模型預測能力良好，可以指導實際生產實踐.

(2) 模擬結果表明，導磁體可以將原本自由散布在空間中的磁感線“吸引”到體內，再通過控制開口位置，將體內高密度磁感線引導至待加熱區域，大幅提高該區域的磁場強度.在局部感應加熱技術中，應當采用外形適宜的導磁體，以便提升局部感應加熱效率.

(3) 模擬結果表明，磁感應強度具有與感應電流相似的集膚效應，電磁集膚效應對溫度場分布起到決定性作用.需要快速均勻透熱時，應當根據目標加熱溫度，首先選擇適中的加熱頻率和加熱時長，然后再根據目標加熱范圍，確定加熱功率.本工藝確定的最佳加熱頻率、加熱功率以及加熱時長分別為 40 kHz、52.5 kW以及3 s.

(4) 實驗結果表明，選用數值模擬優化后的加熱工藝參數，加熱溫度符合預期，“尖角化”效果顯著提升.成形后的高強度鋼尖角方管外圓角半徑為0.32 mm，減小約91%，角部厚度為3.14 mm，增加約59%，沒有出現裂紋缺陷，滿足工程應用的安全要求.