膜結構在暴雨積水時材料模型研究

龐 妍， 卿 強， 王沙沙， 張翔宇， 龔景海

(上海交通大學 船舶海洋與建筑工程學院，上海 200240)

膜結構具有質量輕、強度高的特點，被廣泛應用于體育館、機場、煤棚等結構.坡度較小、較平整的膜結構易在暴雨天氣下發生積水而導致結構破壞，因此模擬膜結構遭遇暴雨影響具有必要性.膜材本構模型會直接影響膜面計算變形的大小，但目前在數值模擬中采用的膜材本構模型往往不能準確地反映出實際工作中膜面的形態變化.

膜結構技術規程[1]中建議采用正交比例加載進行重復拉伸試驗確定膜材的彈性模量，因為雙軸拉伸試驗更符合膜材的受力情況.在膜結構和膜材性能的相關研究中[2-6]，通常選擇經過雙軸循環拉伸多次之后已經穩定的曲線作為膜材模型.孫戰金等[7]在預張力測量技術的研究中指出，聚酯纖維類膜材經過多次反復張拉，在消除大部分殘余應變后，膜材的彈性模量基本穩定在一個固定值，通過計算加載曲線的斜率來確定膜材彈性模量，建立膜材線性本構模型；張其林等[8]將第五循環的加載曲線擬合后得到的直線斜率作為試驗所得的彈性模量；黃賽帥等[9]將膜材第二、第三次加載試驗曲線進行擬合得到直線，并取兩次加載的平均值，最終確定膜材的彈性模量和泊松比；Yang等[10]提出了膜材的二階非線性模型，與線性模型相比，該模型能更好地模擬測試數據.

現有文獻多采用循環多次后穩定的加載曲線進行線性化擬合，求解膜材彈性模量，以及建立膜材線性本構模型[11-15]，但并不適用于所有情況.實際上，膜結構在施工完畢后，在遭遇暴雨作用時，膜材并不滿足循環加載多次后已經穩定的要求.進行模擬分析時，膜結構采用的膜材材料模型是否能準確反映膜材實際情況，對結構的安全性有關鍵性影響.若采用的膜材彈性模量與實際值偏差大，則膜面變形的計算結果誤差較大，結構在暴雨天氣下將有被破壞的危險.

為模擬膜結構受暴雨作用時的受力變形特性，本文在某臨時頂蓋樣機上進行均布荷載加載試驗，選擇較平整的膜面區域進行加載，模擬膜面的積水變形.通過膜材的單軸拉伸及雙軸拉伸建立了膜材的線性和雙折線材料模型.基于不同膜材材料模型建立有限元模型進行計算，將數值模擬結果與試驗測得的結果進行比較分析，判斷材料模型選用的合理性，為膜結構的分析設計及遭遇暴雨的數值模擬提供參考.

1 試驗模型

1.1 試驗對象

試驗對象為一跨度為40 m的圓形核電站臨時頂蓋，采用骨架式膜結構，整體模型如圖1所示.

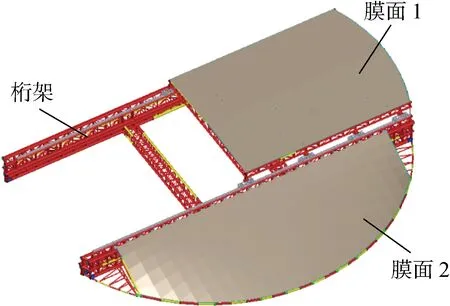
圖1 模型整體示意圖Fig.1 Schematic diagram of overall model

由于排水需求，膜面有一定坡度.如圖2所示，膜面1與平面夾角為2.1°，坡度較小，膜面較平，容易在暴雨天氣下產生積水，引起膜面較大變形.

圖2 膜面1坡度示意圖Fig.2 Schematic diagram of slope of membrane Surface 1

選取膜面1作為試驗加載區域.在暴雨時，雨水作為均布荷載作用在膜面上，因此在膜面上施加均布荷載，模擬其遭遇暴雨時的結構變化.為觀測膜面在均布荷載作用下的變形，采用局部加載的方法，在膜面上選取加載區域如圖3所示，加載區域長3.295 m，寬1.52 m，四周均有鋼桁架支承.

圖3 加載區域示意圖Fig.3 Schematic diagram of loading area

1.2 膜材參數

試驗模型的膜面采用Ferrari1202S2膜材，密度為 1 050 g/m2，經緯向拉伸強度均為112 kN/m，經向撕裂強度為800 N，緯向撕裂強度為650 N，黏結強度為2.4 kN/m.根據設計，膜面張拉后預應力為1 kN/m.

1.3 膜材材料模型

對膜材進行單軸拉伸試驗和應力比(經向：緯向)分別取1∶1、2∶1、1∶2、1∶0、0∶1下的雙軸拉伸試驗，如圖4和圖5所示.

圖4 單軸拉伸試驗Fig.4 Uniaxial tensile test

圖5 雙軸拉伸試驗Fig.5 Biaxial tensile test

由單軸拉伸強度試驗可得到膜材的經、緯向極限抗拉強度，分別為102.85和103.71 kN/m，與膜材材料參數顯示的112 kN/m接近.膜結構技術規程[1]規定膜面應力不允許超過膜材極限抗拉承載力的1/4，故雙軸拉伸試驗的應力峰值為膜材抗拉極限強度的1/4，取26 kN/m.

在雙軸拉伸試驗中，各應力比下均進行3次有效試驗，取3次試驗計算的平均值作為最終結果，膜材在不同應力比下雙軸拉伸的經緯向應力-應變曲線如圖6所示.

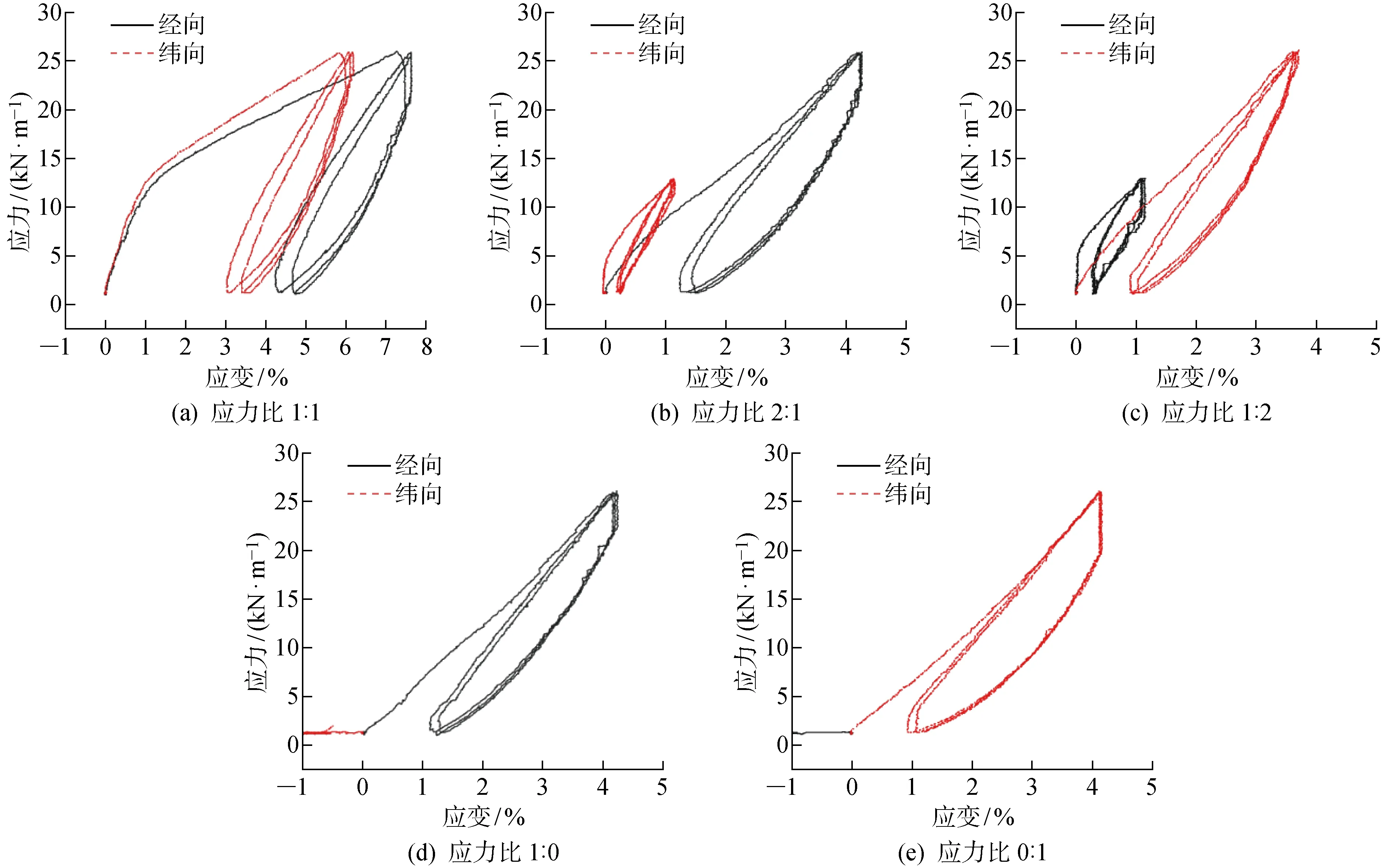
圖6 不同應力比下的應力-應變曲線Fig.6 Strain-stress curves at different stress ratios

通過試驗可確定膜材雙軸本構模型的力學參數，該結構中Ferrari膜材為正交各向異性彈性材料，本構關系由下式確定：

(1)

式中：Nw、Nf分別為十字形膜材試樣經向、緯向荷載；Ew、Ef分別為膜材的經向、緯向彈性模量；εw、εf分別為經向、 緯向應變；νw、νf分別為經向、緯向泊松比；t為膜材厚度.

采用最小二乘法，根據下式可得：

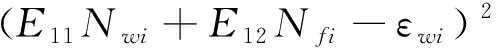
(2)

(3)

(4)

(5)

式中：S為最小二乘法所對應的函數；E11、E22和E12為最小二乘法的待定系數；i為角標，代表雙軸拉伸試驗中測得的每一組數據.

考慮膜材為正交異性材料，E11、E22和E12之間相互獨立，故有

(6)

從而得到3個相互獨立的方程：

(7)

(8)

(9)

將應力比為1∶1、2∶1、1∶2、1∶0、0∶1下雙軸拉伸試驗的應力、應變增量代入式(7)～(9)中，求解線性方程組，即可得到膜材的彈性模量和泊松比.

目前研究多采用膜材線性本構模型，即取應力-應變曲線循環加載段的起點和終點作割線，由割線斜率求得膜材模量.但由圖6可以看出，在第一次加載時，膜材的應力-應變曲線呈現出明顯的非線性.在加載的初始階段，曲線斜率最大，隨著應力的增大，曲線斜率減小即膜材經、緯向彈性模量減小.

建立以下兩種本構模型：線性與雙折線本構模型，分別記為模型1和模型2.模型1為線性模型，取應力-應變曲線第一次循環加載段的起點和終點作割線；模型2為雙折線模型，第一階段取應力-應變曲線第一次循環加載段的起點到應力13 kN/m處作割線，第二階段取應力13 kN/m處到終點作割線.以應力比1∶1時的應力-應變曲線為例，模型1和模型2的割線如圖7所示.

圖7 試驗膜材應力-應變曲線(應力比1∶1)Fig.7 Stress-strain curve at a stress ratio of 1∶1 of membrane material

利用應力比1∶1、2∶1、1∶2、1∶0、0∶1下的應力-應變曲線，分別進行差值計算得到模型1和模型2的膜材力學參數，如表1所示，其中G為切變模量.

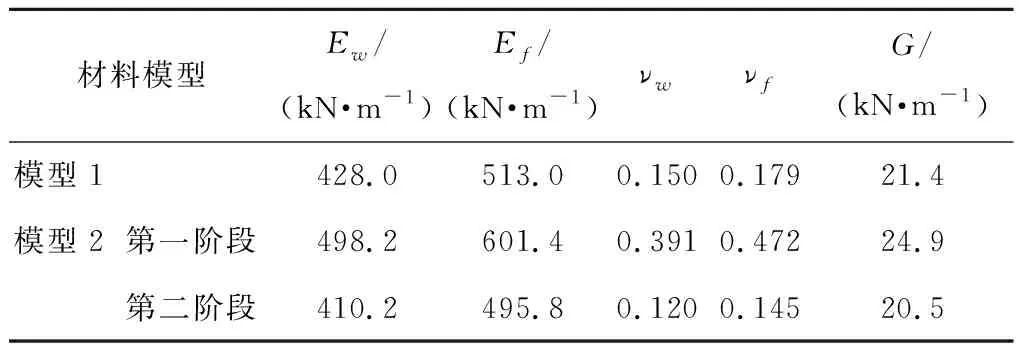
表1 膜材試件彈性模量及泊松比計算結果

2 均布荷載加載試驗

2.1 試驗過程

試驗采用均布荷載模擬膜面遭遇暴雨作用.頂蓋結構具有抵抗17級臺風的需求，因此均布荷載的取值考慮了臺風強度.17級臺風對應的風壓力為2.0 kN/m2，風荷載標準值為5.67 kN/m2，設計值為1.5×5.67 kN/m2=8.505 kN/m2.試驗所施加的均布荷載需大于風荷載設計值，加載時選用30 kg沙袋，分3級進行加載.為模擬均布荷載的效果，以布滿一層為1級荷載，不斷往上疊加沙袋，總共加載193袋.第1級荷載為4.2 kN/m2，第2級荷載為3.3 kN/m2，第3級荷載為2.2 kN/m2，加載完畢后，該膜面所承受的最大荷載即本試驗場布荷載為9.7 kN/m2.膜面上的荷載加載過程如圖8所示.

圖8 均布加載過程圖Fig.8 Uniform load loading process diagram

在加載前以及每一級荷載加載完畢后，待膜面變形穩定，采用PENTAX型全站儀對膜面測點的位置進行測量，測點取加載區域的中心點.

2.2 試驗結果

在各級荷載作用下，膜面最大變形與荷載的關系如圖9所示.在第1級荷載加載時，膜面的高度變化最大，在隨后加載過程中，高度變化速度變慢.在3級荷載加載完畢時，膜面最低點的豎向變形已達到0.184 m.

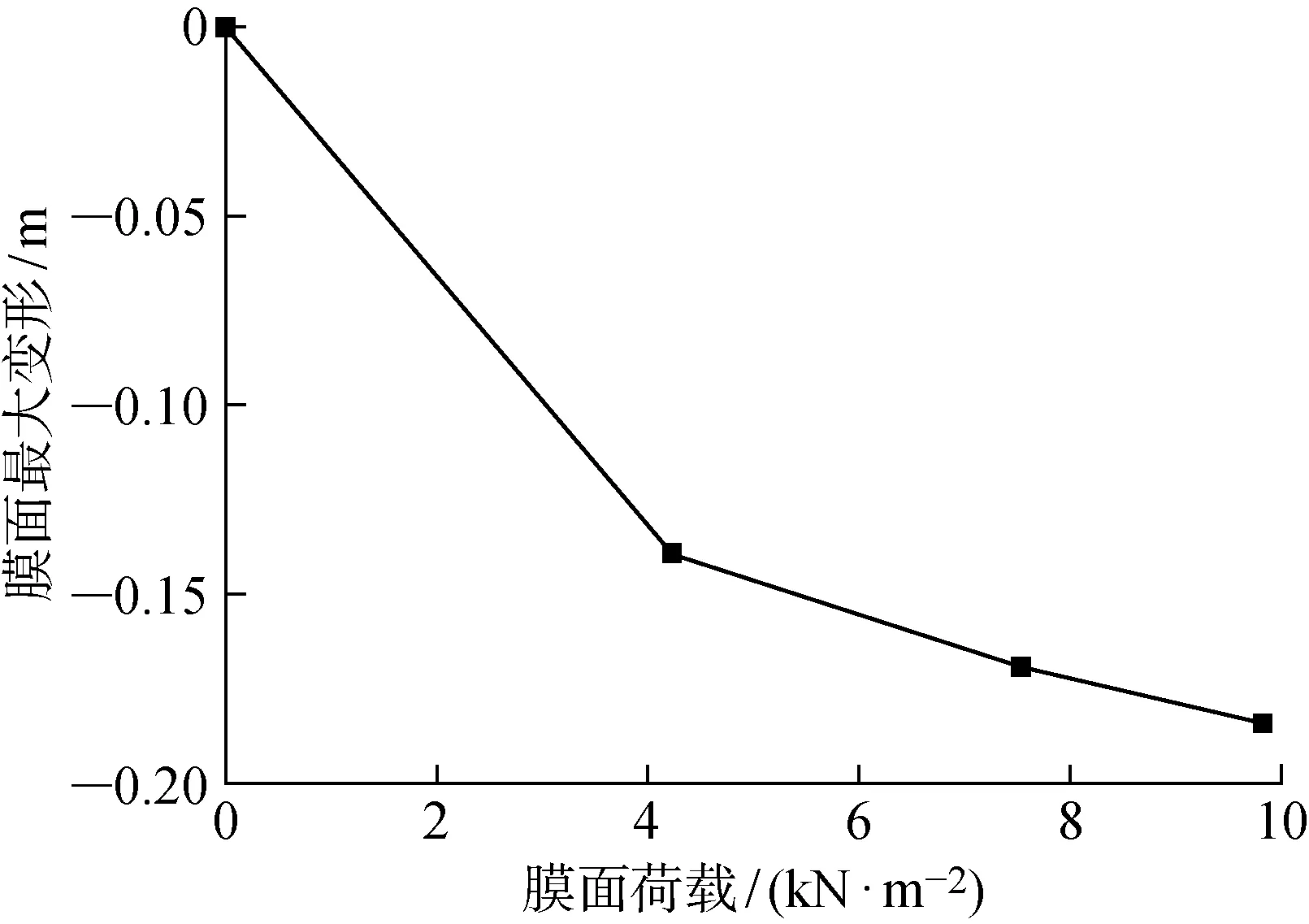
圖9 膜面最大變形與荷載的關系圖Fig.9 Maximum deformation of membrane surface versus load

3 數值模擬

3.1 有限元數值模擬

使用STCAD軟件建立試驗對象的有限元分析模型, 如圖10所示.圖中，加載區域膜面的尺寸為 3.92 m×1.52 m，此處采用三節點膜單元，網格劃分為36×12，如圖11所示.該區域邊緣處膜單元的節點與桁架單元的節點耦合平動方向的自由度.

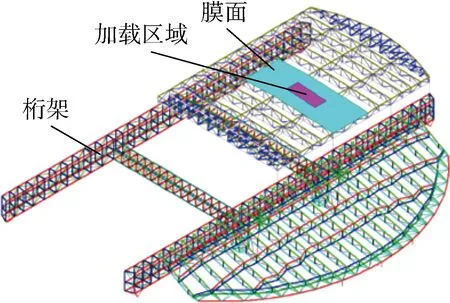
圖10 有限元模型Fig.10 Finite element model

圖11 膜單元網格劃分示意圖Fig.11 Diagram of meshing of membrane elements

采用模型1和模型2分別進行膜材材料模型分析，與材料模型1和模型2對應的有限元模型分別稱為模型A和模型B.

由于本試驗的膜結構在施工時，按設計要求施加經、緯向1 kN/m的初始預應力，故在有限元模型中，對膜面賦予同樣的預應力進行加載過程的受力分析.采用非線性有限元法分析加載過程中的荷載變化和結構受力狀態.

兩個模型在3級荷載加載過程中的變形變化規律一致，第1級荷載加載后膜面變形增量最大，隨后，變形的速度減慢，各級荷載下加載區域膜面的變形如圖12所示.

圖12 各級荷載下加載區域膜面的變形Fig.12 Deformation of membrane surface of loading area at different loads

模型A與模型B的最大變形對比如圖13所示，兩模型變形形態相似.模型A的最大變形為 195.03 mm，模型B的最大變形為181.20 mm，比模型A小7.09%.

圖13 模型A與模型B最大變形對比圖Fig.13 Comparison of maximum deformation between model A and model B

模型A和模型B的加載區域膜面應力(σ)云圖如圖14所示.在第3級荷載作用下，模型A和模型B的膜面經向應力均大于13 kN/m，達到膜材雙折線本構模型的第二階段.

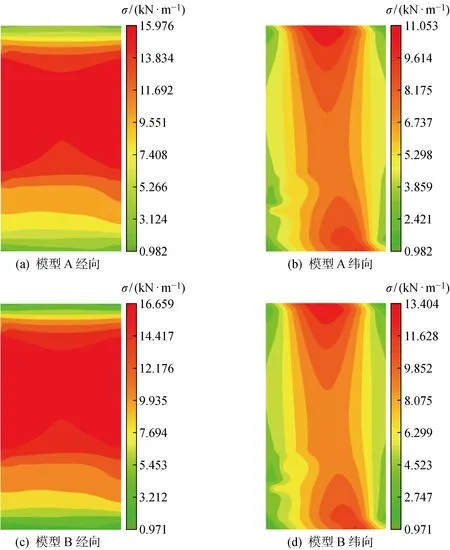
圖14 加載區域膜面的應力云圖Fig.14 Stress cloud image of loading area of membrane

3.2 有限元分析結果與試驗結果對比

試驗和有限元模型得到的膜面最大變形與荷載的關系如圖15 所示.由圖可知，在初始狀態到第3級荷載9.7 kN/m2的加載過程中，有限元模型與試驗的膜面變形變化規律一致.在加載初期，曲線的斜率大，隨著荷載的增加，膜面高度變化大；在加載后期，膜面的高度變化逐漸減緩.

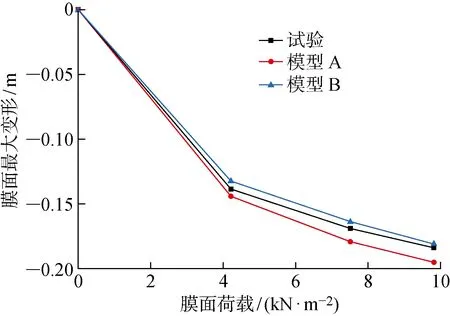
圖15 膜面最大變形與荷載的關系Fig.15 Maximum deformation of membrane surface versus load

試驗測得的膜面最大變形為184 mm，模型A的最大變形為195.03 mm，比試驗結果大5.99%，模型B的最大變形為181.20 mm，比試驗結果小1.52%.模型B的變形比模型A更接近試驗值.局部區域在荷載作用下的試驗與模型A、模型B膜面位置對比如圖16所示.

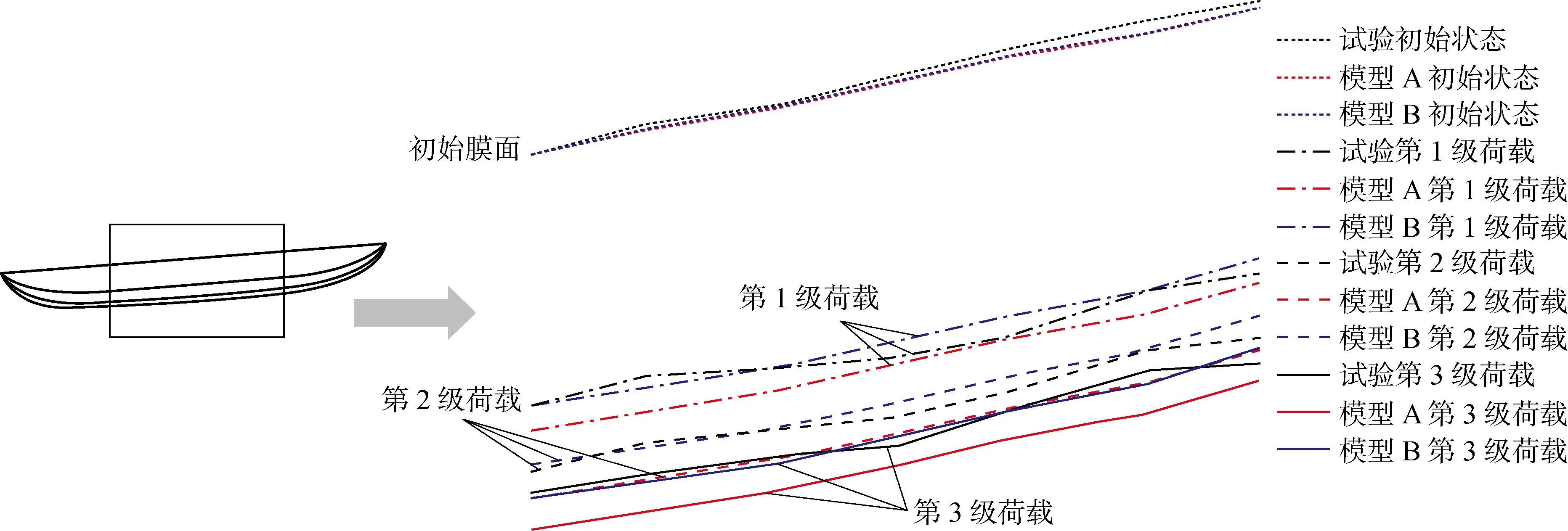
圖16 試驗與有限元模型膜面位置圖Fig.16 Membrane surface of test and finite element models

在整個加載過程中，模型A的變形大于試驗變形，模型B的變形小于模型A.在施加第1級荷載后，兩個有限元模型與實際結構的變形都較為接近，但模型B比模型A更接近.施加第2級荷載后，模型B的變形值仍接近試驗值，而模型A的變形值已明顯偏離試驗值.隨著荷載增加，模型B分析結果與試驗值越來越接近，模型A的分析結果與試驗值的偏差越來越大.

3.3 膜材本構模型的選擇

在工程設計中，常常采用膜材模型1即膜材線性本構模型，但實際上，膜材在加載過程中經、緯向應力不斷增大，膜材的彈性模量會隨應力水平的變化而變化.本文分析表明，考慮該影響的雙折線本構模型可以更好地擬合出膜結構受荷載作用后的變形，其分析結果比線性本構模型更合理.

根據有限元分析結果與試驗結果的對比分析，采用膜材模型2的有限元模型與試驗的實際變形更接近.由圖6的應力-應變曲線可知，在加載的初始階段，膜材經、緯向彈性模量最大，隨著應力的增大，膜材彈性模量減小.在本試驗中，若采用膜材線性本構模型，在加載的初始階段，彈性模量偏小，導致結構分析結果的變形偏大，應力偏小，不利于準確模擬膜結構受荷載作用后的變形和內力狀態.

4 結論

通過對膜結構模型的加載試驗與試驗過程的有限元模擬，得到以下主要結論：

(1) 相較于線性材料本構模型，采用膜材雙折線本構模型更能準確模擬膜結構在荷載作用下的變形.建議在實際工程中，采用考慮應力水平影響的膜材雙折線本構模型，有利于結構的安全.

(2) 實際工程遭受暴雨時，較平的膜面易產生變形和積水，對結構造成危害和危險.因此，當膜材產生一定的變形時，有必要通過張緊裝置將膜材重新張緊，避免產生過大變形.

(3) 采用膜材雙折線本構模型的有限元分析所預測的膜面變形結果較為準確，但在加載的初始階段，有限元模型的變形與試驗結果有一定差值.膜材的彈性模量隨應力比的變化而不斷改變，在下一步的研究中，將對膜材特性進行深入研究，建立更合理的膜材非線性本構模型.