單向熱塑性復(fù)合材料層壓板偏軸拉伸試驗(yàn)及其數(shù)值模擬

張 健， 陳秀華， 陳 勇， 范 寅

(上海交通大學(xué) a. 機(jī)械與動(dòng)力工程學(xué)院； b. 航空航天學(xué)院，上海 200240)

復(fù)合材料由于強(qiáng)度高、剛度大、質(zhì)量輕和抗疲勞等優(yōu)點(diǎn)，在航空航天、能源和交通等領(lǐng)域應(yīng)用廣泛[1].隨著熱塑性預(yù)浸料纖維浸漬技術(shù)及低成本制造技術(shù)的發(fā)展和成熟，熱塑性復(fù)合材料由于高韌性、高損傷容限、生產(chǎn)效率高、易修復(fù)和可回收等眾多優(yōu)點(diǎn)，在商用航空、汽車(chē)和風(fēng)力發(fā)電葉片等領(lǐng)域逐漸得到應(yīng)用[2-4].為了設(shè)計(jì)出一個(gè)能滿足要求的熱塑性復(fù)合材料結(jié)構(gòu)件，在設(shè)計(jì)分析階段需要一個(gè)合適的本構(gòu)方程來(lái)描述熱塑性復(fù)合材料在不同載荷條件下的力學(xué)行為.對(duì)于熱塑性復(fù)合材料，已有試驗(yàn)研究表明AS4/PEEK、C/PPS和AS4/PEKK等熱塑性復(fù)合材料在剪切方向會(huì)由于塑性變形而表現(xiàn)出顯著的非線性行為[5-7].另外，由于不同組分的力學(xué)性能存在較大差異，復(fù)合材料內(nèi)部的應(yīng)力分布極不均勻，其損傷模式極為復(fù)雜，包括纖維斷裂、基體斷裂和纖維/基體脫黏等，這些損傷模式可以單獨(dú)或者同時(shí)發(fā)生[8].在加載的過(guò)程中，復(fù)合材料將會(huì)出現(xiàn)上述損傷并逐漸演化直至失去承載能力.因此，為了準(zhǔn)確預(yù)測(cè)熱塑性復(fù)合材料的非線性力學(xué)行為和極限強(qiáng)度，在本構(gòu)方程中應(yīng)同時(shí)考慮塑性和損傷的影響.

連續(xù)介質(zhì)損傷力學(xué)為復(fù)合材料的有限元分析提供了判斷損傷起始和損傷演化的框架，國(guó)內(nèi)外學(xué)者在此基礎(chǔ)上建立了眾多的彈性損傷模型[9-17].彈性損傷模型假設(shè)復(fù)合材料在破壞前表現(xiàn)為線彈性，該模型適用于描述在加載過(guò)程中應(yīng)力-應(yīng)變曲線表現(xiàn)為線彈性的復(fù)合材料.但對(duì)于在加載過(guò)程中塑性行為較為明顯的熱塑性復(fù)合材料，彈性損傷模型的模擬效果并不理想.例如Maa等[18]使用彈性損傷模型分析AS4/PEEK開(kāi)孔層壓板的極限拉伸載荷，模擬結(jié)果與試驗(yàn)結(jié)果誤差在10%以上，最大的誤差達(dá)到了25.83%，誤差較大的原因?yàn)槟Ｐ退僭O(shè)的纖維方向?yàn)榇嘈詳嗔巡⒉荒軠?zhǔn)確模擬實(shí)際的損傷演化.上述研究表明，對(duì)于在加載過(guò)程中產(chǎn)生了塑性變形的熱塑性復(fù)合材料，彈性損傷模型將產(chǎn)生較大的誤差；Xiao[19]的研究表明，未考慮塑性效應(yīng)會(huì)低估復(fù)合材料結(jié)構(gòu)的能量吸收能力，從而導(dǎo)致較大的誤差.

為了同時(shí)考慮復(fù)合材料的塑性行為和損傷累積，以往研究在彈性損傷模型中加入塑性項(xiàng)，即在塑性力學(xué)的框架內(nèi)建立彈塑性損傷模型.Ladeveze等[20]提出一種復(fù)合材料彈塑性損傷模型，該模型不僅計(jì)入了塑性變形，同時(shí)也考慮了由基體開(kāi)裂和纖維/基體脫黏而造成的剛度退化，但模型不考慮沿纖維方向的損傷，與試驗(yàn)結(jié)果對(duì)比顯示，該模型能夠準(zhǔn)確模擬復(fù)合材料的塑性力學(xué)行為和破壞行為；陳靜芬[8]提出一種基于單參數(shù)塑性模型[21]和Hashin準(zhǔn)則[22]的二維彈塑性損傷本構(gòu)模型.為解決有限元隱式計(jì)算中由于應(yīng)變軟化而導(dǎo)致的計(jì)算困難問(wèn)題，作者對(duì)損傷變量進(jìn)行了黏性正則化.結(jié)果表明該模型能夠準(zhǔn)確預(yù)測(cè)存在顯著塑性力學(xué)行為的復(fù)合材料的破壞載荷，但該模型忽略了層間應(yīng)力的影響，因而對(duì)于預(yù)測(cè)包含分層損傷的復(fù)合材料強(qiáng)度問(wèn)題顯得不夠準(zhǔn)確.

本文對(duì)不同角度的單向AS4/PEEK層壓板進(jìn)行了偏軸拉伸試驗(yàn)和相應(yīng)的數(shù)值模擬.通過(guò)對(duì)斷裂面的觀察，分析了斷裂面角度與鋪層角度存在差異的原因.對(duì)不同角度單向?qū)訅喊宓膽?yīng)力-應(yīng)變曲線的分析表明，在破壞前纖維方向僅有線彈性行為，將Sun等[21]提出的三維塑性勢(shì)函數(shù)進(jìn)行了簡(jiǎn)化，塑性勢(shì)函數(shù)中的參數(shù)通過(guò)信任域反射算法計(jì)算得到.結(jié)合LaRC05準(zhǔn)則[23]和裂紋帶理論[24]建立了三維彈塑性損傷本構(gòu)模型，通過(guò)編寫(xiě)基于Abaqus的用戶自定義材料子程序VUMAT并將其應(yīng)用于不同鋪層角度的偏軸拉伸試驗(yàn)的數(shù)值模擬中，與試驗(yàn)獲得的結(jié)果進(jìn)行對(duì)比，驗(yàn)證了該模型的正確性.本文提出的三維彈塑性損傷模型考慮了除纖維方向外各方向的塑性變形并以及斷裂面角度對(duì)復(fù)合材料損傷的影響，與文獻(xiàn)[8,18]相比，該模型能更加準(zhǔn)確地預(yù)測(cè)試驗(yàn)件的拉伸強(qiáng)度.

1 試驗(yàn)及結(jié)果分析

1.1 試驗(yàn)設(shè)置

試驗(yàn)采用單向AS4/PEEK層壓板，共有7種鋪層，分別為[0]8、[15]20、[30]20、[45]20、[60]20、[80]20和[90]16.其中，[0]8鋪層的試驗(yàn)件尺寸為250 mm×15 mm×1.12 mm，[90]16鋪層的試驗(yàn)件尺寸為250 mm×25 mm×2.24 mm，其余試驗(yàn)件的尺寸為250 mm×25 mm×2.8 mm.試驗(yàn)件兩端粘有加強(qiáng)片，[0]8鋪層加強(qiáng)片的尺寸為25 mm×15 mm×1.5 mm，其余試驗(yàn)件加強(qiáng)片的尺寸均為 25 mm×25 mm×1.5 mm，斜削角均為90°.每種鋪層有5個(gè)試驗(yàn)件.

圖1 偏軸拉伸試驗(yàn)的試驗(yàn)設(shè)備Fig.1 Test equipment for off-axis tensile test

試驗(yàn)使用UTM5105X微機(jī)控制電子萬(wàn)能力學(xué)試驗(yàn)機(jī)進(jìn)行加載，如圖1所示.該試驗(yàn)機(jī)最大載荷為100 kN，準(zhǔn)確度精度為0.5級(jí)；使用應(yīng)變片測(cè)量試驗(yàn)件的應(yīng)變，應(yīng)變片型號(hào)為BX120-3AA，精度等級(jí)為A.試驗(yàn)根據(jù)ASTM D 3039/D 3039M-17[25]標(biāo)準(zhǔn)進(jìn)行，采用位移加載，加載速度為5 mm/min.

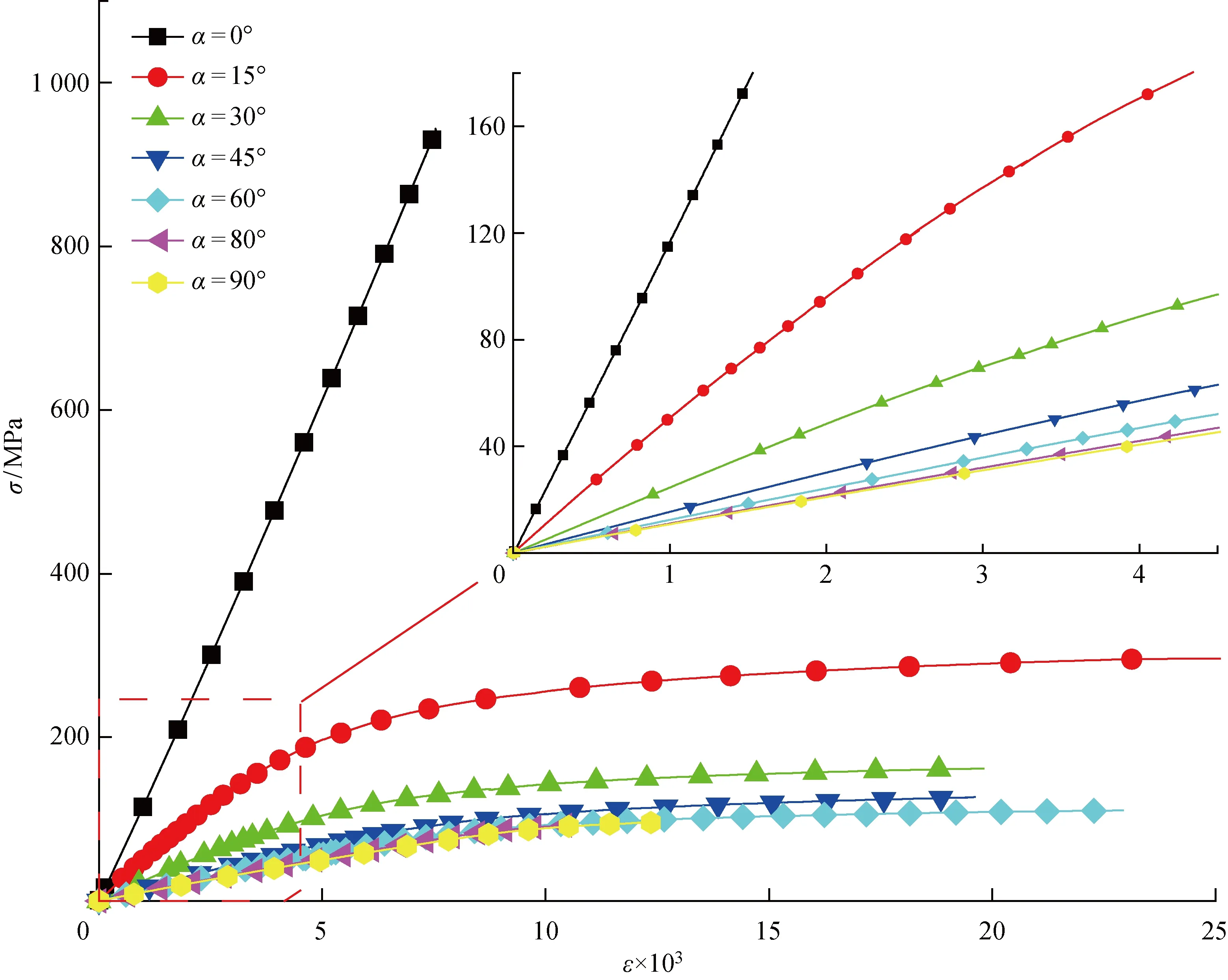
圖2 偏軸拉伸應(yīng)力-應(yīng)變曲線Fig.2 Stress-strain curves of off-axis tensile

1.2 試驗(yàn)結(jié)果及分析

采用ASTM D3039/D3039M-17[25]提出的方法對(duì)試驗(yàn)數(shù)據(jù)進(jìn)行處理，拉伸應(yīng)力的計(jì)算公式為

(1)

式中：σi為第i個(gè)點(diǎn)的拉伸應(yīng)力；Pi為第i個(gè)點(diǎn)的力；A為試驗(yàn)件的橫截面積.

偏軸拉伸試驗(yàn)的應(yīng)力-應(yīng)變(σ-ε)曲線如圖2所示.從應(yīng)力-應(yīng)變曲線可知，當(dāng)偏軸角度為α=0°時(shí)，試驗(yàn)件在破壞前的力學(xué)行為都表現(xiàn)為線彈性；隨著偏軸角度的逐漸增加，試驗(yàn)件的力學(xué)行為首先表現(xiàn)為線彈性，在應(yīng)力超過(guò)一定范圍后表現(xiàn)出明顯的非線性行為；當(dāng)偏軸角度在80°～90°之間時(shí)，試驗(yàn)件的力學(xué)行為只有一小段的線彈性行為，隨后發(fā)生斷裂，原因是這些偏軸角度纖維已經(jīng)不能承受足夠的載荷，在表現(xiàn)出塑性變形前基體已經(jīng)發(fā)生了斷裂破壞.

不同鋪層的破壞模式、破壞部位和斷裂面角度總結(jié)如表1所示.對(duì)比不同試驗(yàn)件的斷裂面角度和偏軸角度，斷裂面角度與偏軸角度的差異在 -1°～2°之間.破壞后的試驗(yàn)件圖片如圖3(a)所示，斷裂面的顯微照片如圖3(b)所示.斷裂面內(nèi)觀察到的主要是基體的斷裂，在基體的斷裂處可以觀察到裸露的纖維，纖維只有少數(shù)發(fā)生了斷裂，未發(fā)生斷裂的纖維沒(méi)有觀察到明顯的偏轉(zhuǎn).對(duì)斷裂面的觀察和分析表明，斷裂面角度與偏軸角度存在差異的原因?yàn)樵谠囼?yàn)件的制造過(guò)程中， 層壓板的鋪層角度與設(shè)定的角度存在一定的誤差.

表1 不同鋪層的破壞模式、破壞部位及斷裂面角度[25]

圖3 試驗(yàn)結(jié)束后的試驗(yàn)件及斷裂面Fig.3 Test specimens and fracture surface after test

2 數(shù)值模擬設(shè)置

2.1 三維彈塑性損傷模型

由試驗(yàn)結(jié)果可知，單向AS4/PEEK層壓板在偏軸拉伸載荷作用下存在顯著的由塑性變形引起的非線性力學(xué)行為及破壞行為.為了準(zhǔn)確模擬上述行為，需要建立一個(gè)包含彈性模型、塑性模型和損傷起始及演化模型的三維彈塑性損傷模型.

2.1.1彈性模型 在線彈性階段，本構(gòu)關(guān)系采用三維模型.對(duì)于正交各向異性層壓板，其典型的應(yīng)力-應(yīng)變關(guān)系為

(2)

式中：

(3)

(4)

(5)

(6)

(7)

(8)

C44=G12

(9)

C55=G23

(10)

C66=G13

(11)

(12)

式中：E1、E2和E3為彈性模量；G12、G23和G13為剪切模量；ν12、ν13和ν23為泊松比；σij(i,j=1, 2, 3)為材料坐標(biāo)系下的應(yīng)力；εij(i,j=1, 2, 3)為材料坐標(biāo)系下的應(yīng)變.

2.1.2塑性模型 本模型采用的塑性屈服函數(shù)為

(13)

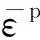
Fp(σ)=

(14)

式中：a66為復(fù)合材料各向異性程度的參數(shù)，假定其值與材料有關(guān).

等效應(yīng)力定義為

(15)

采用關(guān)聯(lián)流動(dòng)法則確定塑性應(yīng)變?cè)隽繛?/p>

(16)

式中：dλ為比例因子.

為保證單位體積塑性功率(dWp)相等，有

(17)

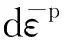
(18)

強(qiáng)化函數(shù)采用Sun等[21]提出的冪函數(shù)形式的各向同性強(qiáng)化函數(shù)，為

(19)

式中：β和n為材料參數(shù)，可通過(guò)擬合等效應(yīng)力-等效塑性應(yīng)變曲線得到.

塑性勢(shì)函數(shù)中的參數(shù)a66可以通過(guò)偏軸拉伸試驗(yàn)得到[21, 27].如圖4所示，x-y坐標(biāo)系為整體坐標(biāo)系，1-2坐標(biāo)系為材料坐標(biāo)系，x軸和1軸之間有一個(gè)大小為θ的夾角，在平行于x軸的拉伸載荷的作用下，復(fù)合材料層壓板的受力狀態(tài)視為平面應(yīng)力狀態(tài).將層壓板在整體坐標(biāo)系的應(yīng)力轉(zhuǎn)換到材料坐標(biāo)系，轉(zhuǎn)換公式為

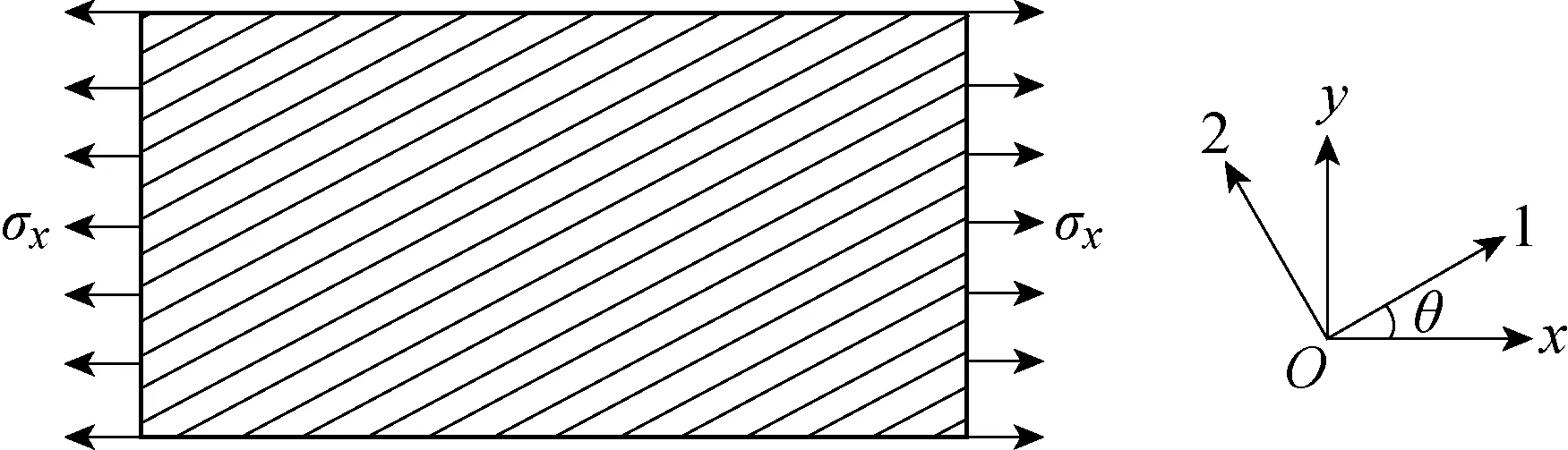
圖4 偏軸拉伸試驗(yàn)示意圖Fig.4 Schematic diagram of off-axis tensile test

σ11=cos2θσx

(20)

σ22=sin2θσx

(21)

σ12=-sinθcosθσx

(22)

式中：σx為x方向的應(yīng)力.將式(20)～式(22)代入式(15)可得等效應(yīng)力為

(23)

式中:

(24)

由塑性應(yīng)變?cè)隽康淖鴺?biāo)轉(zhuǎn)換可得

(25)

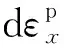
(26)

假設(shè)材料具有顯著的塑性效應(yīng)，且滿足小變形假設(shè)，則總應(yīng)變?cè)隽靠梢苑纸鉃閺椥詰?yīng)變?cè)隽亢退苄詰?yīng)變?cè)隽績(jī)刹糠諿8]，即

(27)

故x方向的塑性應(yīng)變?cè)隽靠梢员硎緸?/p>

(28)

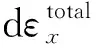
(29)

通過(guò)上述變換，可將偏軸拉伸試驗(yàn)獲得的應(yīng)力-應(yīng)變曲線轉(zhuǎn)換為等效應(yīng)力-等效塑性應(yīng)變曲線.對(duì)于不同角度的偏軸拉伸試驗(yàn)，經(jīng)過(guò)轉(zhuǎn)換后的等效應(yīng)力-等效塑性應(yīng)變曲線應(yīng)該是一致的，故可以通過(guò)選取適當(dāng)?shù)腶66的值使得不同角度的等效應(yīng)力-等效塑性應(yīng)變曲線重合.對(duì)于a66的選取，目前有試錯(cuò)法[21]和信任域反射算法[28]等計(jì)算方法.本文采用Jang等[28]提出的信任域反射算法進(jìn)行計(jì)算.具體計(jì)算流程為：首先設(shè)定a66的初值，此處設(shè)定為0.5，然后采用式(20)～式(29)將試驗(yàn)獲得的不同角度的應(yīng)力和應(yīng)變數(shù)據(jù)變換為等效應(yīng)力和等效塑性應(yīng)變數(shù)據(jù)，將等效應(yīng)力視為等效塑性應(yīng)變的函數(shù)，通過(guò)最小化目標(biāo)函數(shù)來(lái)獲得a66.目標(biāo)函數(shù)的形式為

(30)

(θ1,θ2=15°, 30°, 45°, 60°, 80°, 90°)

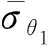
2.1.3損傷起始及演化模型 對(duì)于纖維拉伸損傷，本模型采用最大應(yīng)力準(zhǔn)則來(lái)預(yù)測(cè)，即

(31)

式中：Xt為纖維方向的拉伸強(qiáng)度.當(dāng)fft≥1時(shí)，發(fā)生纖維拉伸損傷.

為了預(yù)測(cè)基體損傷，本模型采用LaRC05準(zhǔn)則[23].該準(zhǔn)則認(rèn)為基體損傷的發(fā)生只與潛在斷裂面上的正應(yīng)力(σn)和兩個(gè)剪應(yīng)力(σnT和σnL)有關(guān)，表達(dá)式為

(32)

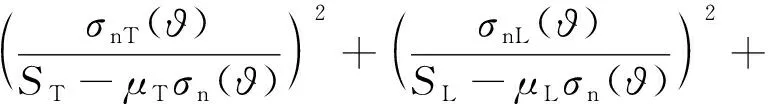
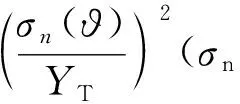
(33)

(34)

式中：?為潛在斷裂面角度，范圍為0°～180°；ST為橫向剪切強(qiáng)度；SL為縱向剪切強(qiáng)度；μT為橫向摩擦系數(shù)；μL為縱向摩擦系數(shù)；YT為基體抗拉強(qiáng)度；Yc為基體抗壓強(qiáng)度；φ0為純橫向壓縮破壞的斷裂面的角度，對(duì)于碳纖維增強(qiáng)復(fù)合材料，試驗(yàn)[29]測(cè)定其值范圍為φ0=53°±2°.當(dāng)基體最大應(yīng)力fmt≥1時(shí)，發(fā)生基體拉伸損傷.

在使用失效準(zhǔn)則對(duì)復(fù)合材料的損傷模式進(jìn)行預(yù)測(cè)后，需要采用適當(dāng)?shù)膿p傷變量來(lái)模擬復(fù)合材料發(fā)生損傷后的力學(xué)行為.本模型使用的損傷變量包括纖維拉伸損傷變量(dft)和基體拉伸損傷變量(dmt)，損傷變量從損傷起始時(shí)的0逐漸演化為完全退化時(shí)的1[30].損傷變量的更新采用Donadon等[31]提出的形式，即

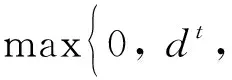
(35)

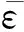
(36)

式中：εf為最終失效時(shí)的應(yīng)變.

對(duì)于纖維的損傷，當(dāng)前增量步的等效應(yīng)變對(duì)應(yīng)于1方向上的應(yīng)變分量，損傷開(kāi)始時(shí)的應(yīng)變和最終失效時(shí)的應(yīng)變的計(jì)算公式為

(37)

(38)

式中：Gft為纖維拉伸破壞斷裂能；L為特征長(zhǎng)度.

對(duì)于基體的損傷，由于在斷裂面上的拉應(yīng)力會(huì)促進(jìn)基體的損傷，損傷開(kāi)始時(shí)的應(yīng)變和最終失效時(shí)的應(yīng)變的計(jì)算相對(duì)更加復(fù)雜.當(dāng)滿足式(33)的失效準(zhǔn)則時(shí)，基體發(fā)生損傷，此時(shí)的等效應(yīng)力和等效應(yīng)變?yōu)?/p>

(39)

(40)

(41)

對(duì)于混合失效情形，基體失效的斷裂能為

(42)

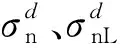
(43)

當(dāng)層壓板發(fā)生基體損傷時(shí)，通過(guò)式(32)將應(yīng)力旋轉(zhuǎn)到斷裂面上，對(duì)斷裂面上的應(yīng)力進(jìn)行軟化，為了考慮反向載荷對(duì)裂紋閉合的影響，斷裂面上的正應(yīng)力只在其為拉伸應(yīng)力時(shí)進(jìn)行軟化，斷裂面上的應(yīng)力軟化式為

(44)

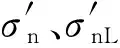
Matzenmiller等[32]認(rèn)為纖維的斷裂、屈曲和壓縮破壞會(huì)對(duì)基體的損傷演化產(chǎn)生影響，故纖維損傷導(dǎo)致的應(yīng)力軟化計(jì)算公式為

(45)

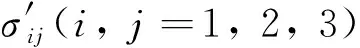
2.2 數(shù)值模擬設(shè)置

依據(jù)三維彈塑性損傷模型的數(shù)值算法編寫(xiě)基于Abaqus的用戶自定義材料子程序VUMAT，其計(jì)算流程如圖5所示.

計(jì)算過(guò)程采用位移增量逐級(jí)加載的方式，在第n+1步的具體計(jì)算步驟如下.

(2) 假定當(dāng)前增量步的塑性應(yīng)變張量和等效塑性應(yīng)變與上一增量步一致，計(jì)算試應(yīng)力為

(46)

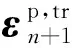
(3) 檢查屈服條件：

(47)

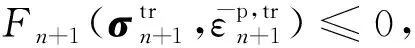
(4) 采用Newton-Raphson方法迭代求解非線性方程：

(48)

表2 AS4/PEEK性能參數(shù)Tab.2 Properties of AS4/PEEK

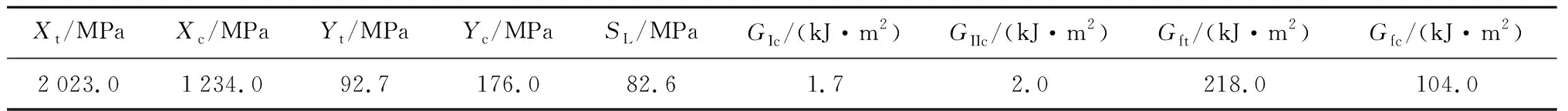
表3 AS4/PEEK的強(qiáng)度及斷裂能Tab.3 Strength and fracture energy of AS4/PEEK

首先初始化參量：

(49)

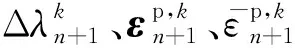
其次計(jì)算第k+1次迭代的比例因子增量為

(50)

并更新第k+1次迭代的塑性應(yīng)變張量和等效塑性應(yīng)變?yōu)?/p>

(51)

再次計(jì)算試應(yīng)力為

(52)

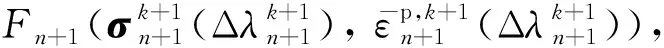
Ftol(=10-6)

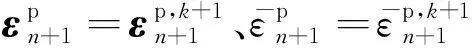
(5) 判斷是否發(fā)生損傷起始.

首先計(jì)算fft，如果fft≥1，則計(jì)算纖維損傷變量dft；否則dft=0.

然后計(jì)算fmt，如果fmt≥1，則計(jì)算基體損傷變量dmt；否則dmt=0.

(6) 更新應(yīng)力，進(jìn)入下一增量步.

AS4/PEEK材料的性能參數(shù)、強(qiáng)度及斷裂能[33-35]如表2和表3所示.其中，Gfc為纖維壓縮壓縮破壞斷裂能，Xc為纖維壓縮破壞斷裂能.為了減少計(jì)算量，有限元模型不考慮加強(qiáng)片部分，模型長(zhǎng)度為200 mm，其余尺寸與試驗(yàn)件尺寸一致，模型的鋪層包含試驗(yàn)件的7種鋪層.有限元模型的單元類型為C3D8R，厚度方向的單元尺寸為0.14 mm，長(zhǎng)度和寬度方向的單元尺寸為1 mm.在加載過(guò)程中，如圖1(b)所示試驗(yàn)件的上邊界在x、y和z的3個(gè)方向的位移保持一致，對(duì)試驗(yàn)前后的試驗(yàn)件的上邊界橫截面尺寸進(jìn)行測(cè)量，上邊界橫截面尺寸變形微小，可以將試驗(yàn)件的上邊界視作剛性平面，故有限元模型的邊界條件為一端約束x、y和z方向的位移Ux、Uy和Uz，另一端與參考點(diǎn)耦合， 在參考點(diǎn)上施加x方向位移并約束y和z方向的位移.將一組節(jié)點(diǎn)耦合至參考點(diǎn)并在參考點(diǎn)施加位移載荷已在文獻(xiàn)[10,34,36]中使用廣泛.包含邊界條件的有限元模型如圖6所示.

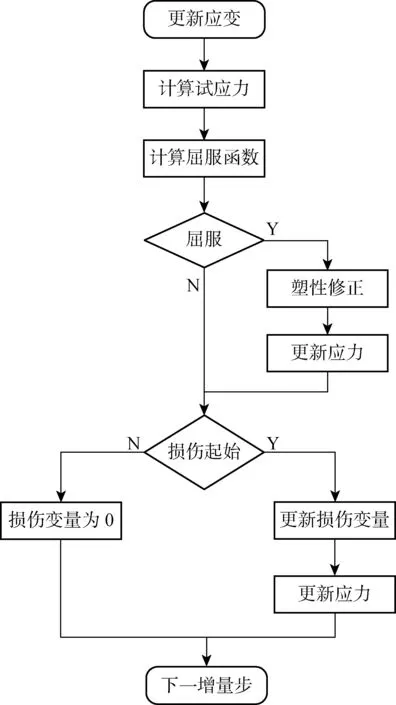
圖5 VUMAT計(jì)算流程圖Fig.5 Flow chart of subroutine VUMAT

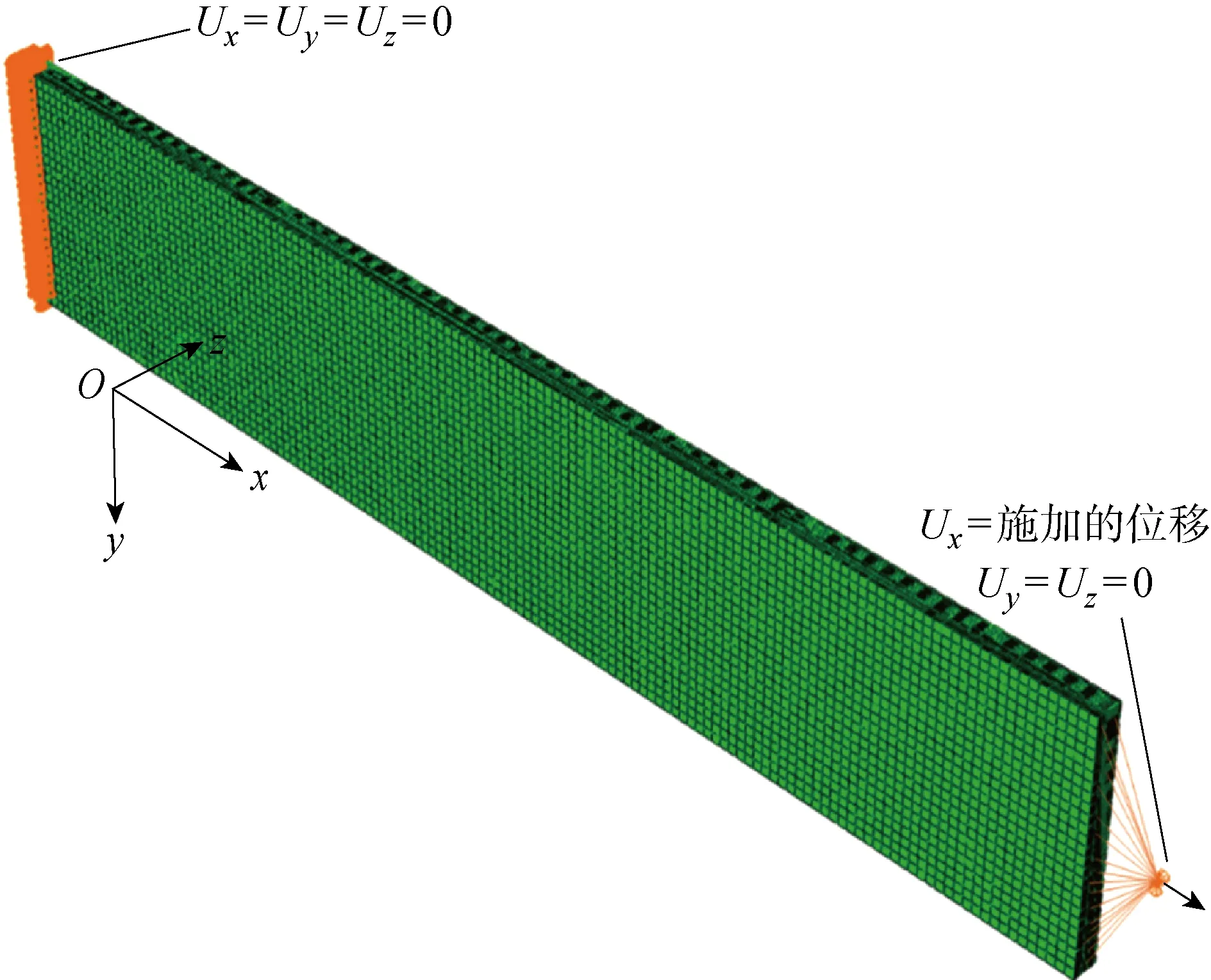
圖6 包含邊界條件的有限元模型Fig.6 Finite element model with boundary conditions

3 數(shù)值模擬結(jié)果及分析

3.1 塑性參數(shù)的確定

利用MATLAB軟件編寫(xiě)程序進(jìn)行塑性參數(shù)的求解.模型假設(shè)纖維方向是線彈性的，故[0]8鋪層的數(shù)據(jù)未考慮，對(duì)其余鋪層獲得的應(yīng)力-應(yīng)變曲線進(jìn)行計(jì)算，最優(yōu)化目標(biāo)函數(shù)后獲得的塑性參數(shù)為a66=1.50，擬合等效應(yīng)力-等效塑性應(yīng)變曲線獲得的硬化函數(shù)的參數(shù)值為β=292.67，n=0.134 6.選取上述值繪制的等效應(yīng)力-等效塑性應(yīng)變曲線如圖7所示，其中ξ為鋪層角度.擬合得到的等效應(yīng)力-等效塑性應(yīng)變曲線與試驗(yàn)值存在誤差的原因有兩個(gè)：一是試驗(yàn)測(cè)量獲得的應(yīng)力和應(yīng)變數(shù)據(jù)存在一定的測(cè)量誤差；二是在進(jìn)行數(shù)值優(yōu)化過(guò)程中存在的舍入誤差.

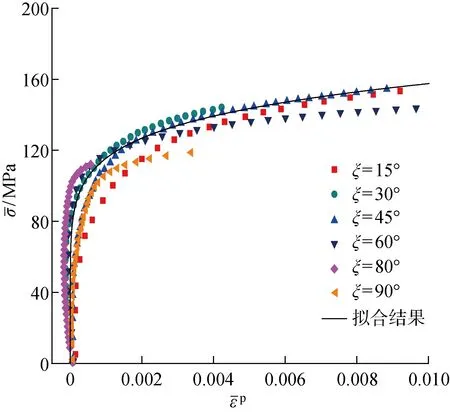
圖7 等效應(yīng)力-等效塑性應(yīng)變曲線Fig.7 Equivalent stress-equivalent plastic strain curve

3.2 數(shù)值模擬結(jié)果

數(shù)值模擬獲得的不同角度的應(yīng)力-應(yīng)變曲線與試驗(yàn)獲得的應(yīng)力-應(yīng)變曲線的對(duì)比如圖8所示，可以看出數(shù)值模擬獲得的應(yīng)力-應(yīng)變曲線與試驗(yàn)獲得的應(yīng)力-應(yīng)變曲線吻合較好，表明本模型能夠較為準(zhǔn)確地模擬單向AS4/PEEK層壓板的塑性效應(yīng).

試驗(yàn)和數(shù)值模擬預(yù)測(cè)的拉伸強(qiáng)度見(jiàn)表4，表中實(shí)驗(yàn)值為5件試驗(yàn)件的拉伸強(qiáng)度的平均值.從表4可知，在試驗(yàn)件厚度相同的情況下，隨著偏軸角度的增加，拉伸強(qiáng)度逐漸下降.數(shù)值模擬預(yù)測(cè)的拉伸強(qiáng)度與實(shí)驗(yàn)值的最大誤差為19.05%，不超過(guò)20%，表明該模型適用于預(yù)測(cè)單向AS4/PEEK層壓板偏軸拉伸的拉伸強(qiáng)度.

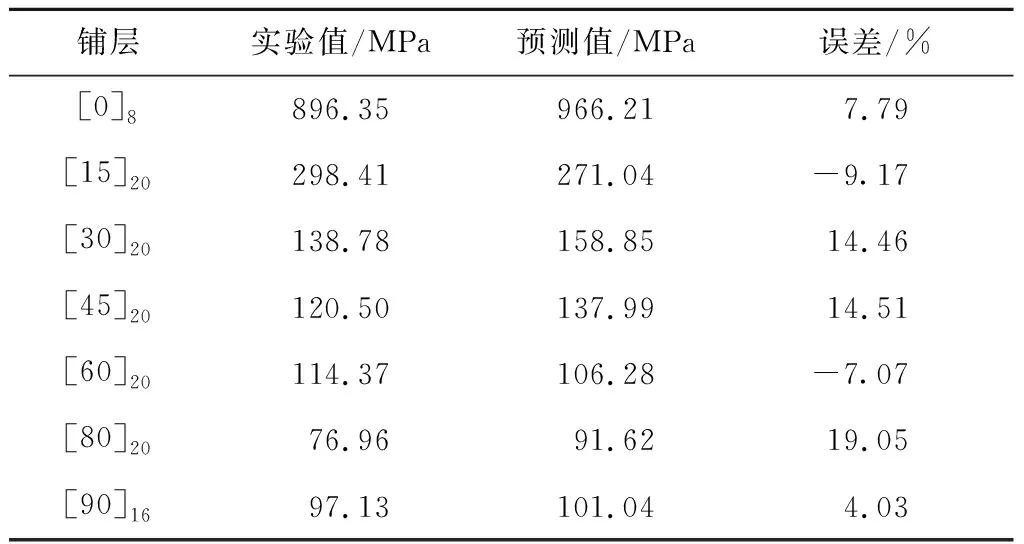
表4 拉伸強(qiáng)度及誤差的對(duì)比Tab.4 Comparison of tensile strength and error

[45]20鋪層數(shù)值模擬和試驗(yàn)獲得的應(yīng)力-總應(yīng)變(εtotal)曲線對(duì)比如圖9所示.結(jié)合圖10的塑性應(yīng)變(εp)-總應(yīng)變曲線可知，當(dāng)總應(yīng)變?cè)?1.5×10-3以下時(shí)，各個(gè)方向都不存在塑性變形，此時(shí)層壓板表現(xiàn)為線彈性；隨著總應(yīng)變的增大，除纖維方向外其余方向的塑性變形逐漸增大，使得層壓板表現(xiàn)出明顯的非線性力學(xué)行為；當(dāng)總應(yīng)變達(dá)到 22.7×10-3時(shí)，應(yīng)力出現(xiàn)急劇下降，表明此時(shí)層壓板已經(jīng)完全破壞.從圖10可以看出，塑性變形主要發(fā)生在1-2平面內(nèi)和3方向，且1-2平面內(nèi)的剪切塑性應(yīng)變約為2方向和3方向的塑性應(yīng)變的3倍，表明剪切變形在塑性變形中處于主導(dǎo)地位.

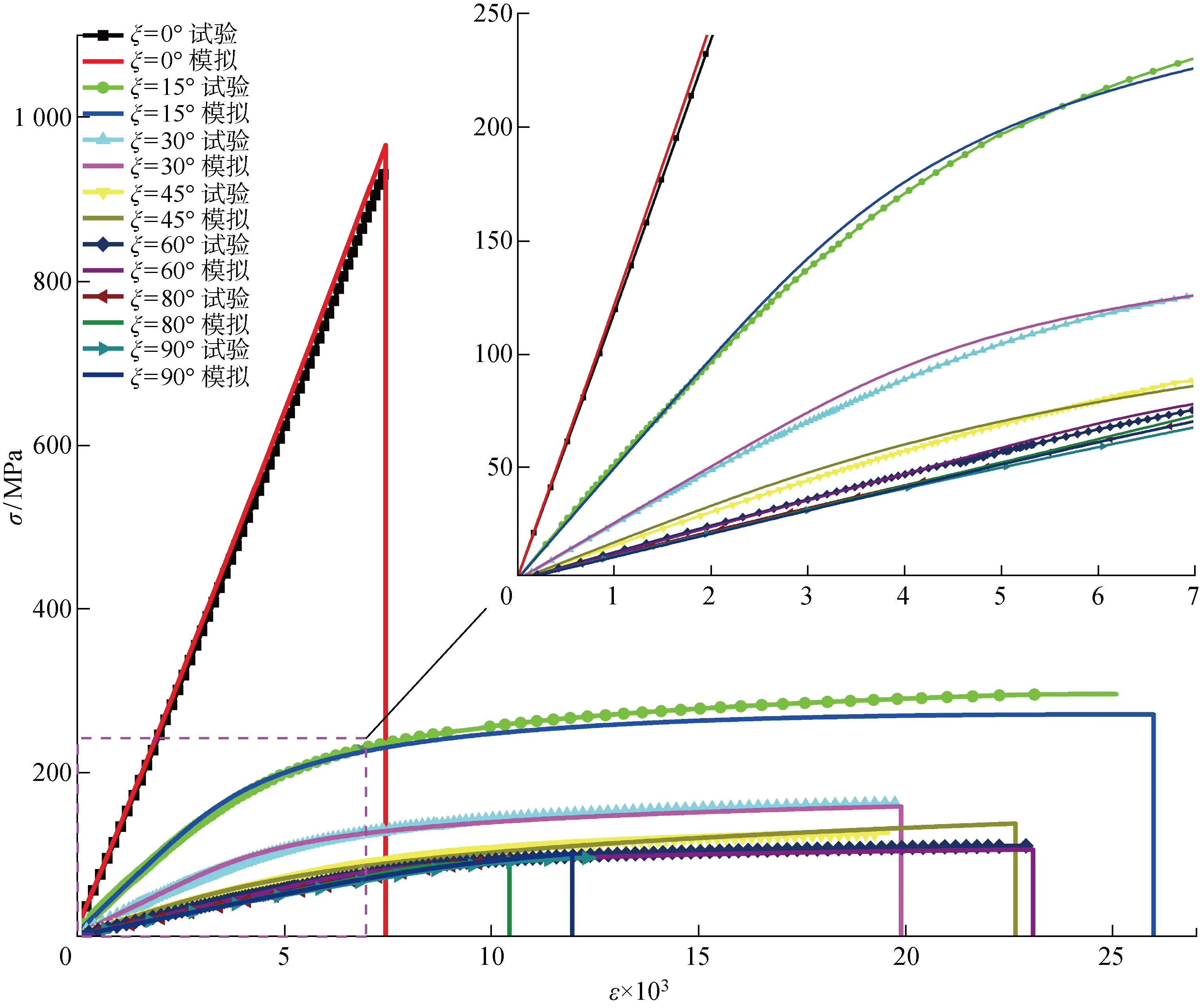
圖8 數(shù)值模擬與試驗(yàn)的應(yīng)力-應(yīng)變曲線對(duì)比Fig.8 Comparison of stress-strain curves between numerical simulation and test

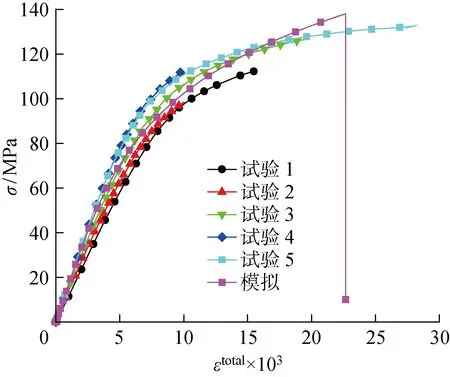
圖9 [45]20鋪層試驗(yàn)與數(shù)值模擬應(yīng)力-總應(yīng)變曲線對(duì)比Fig.9 Comparison of stress-total strain curves between experiment and numerical simulation of [45]20 specimens

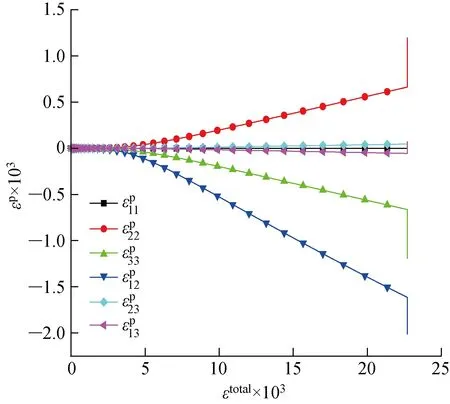
圖10 塑性應(yīng)變-總應(yīng)變曲線Fig.10 Plastic strain-total strain curve

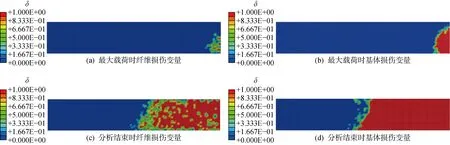
圖11 [45]20鋪層損傷變量Fig.11 Damage variables of [45]20 specimens

最大載荷和分析結(jié)束時(shí)的損傷變量(δ)云圖如圖11所示，當(dāng)損傷變量值為0時(shí)表示未發(fā)生破壞，損傷變量值為1時(shí)表示已經(jīng)完全破壞.模擬結(jié)果表明，當(dāng)載荷達(dá)到7.34 kN時(shí)，層壓板首先在端部的邊緣發(fā)生基體破壞；隨著載荷的增加，在基體的破壞部位附近發(fā)生纖維破壞，然后基體破壞和纖維破壞開(kāi)始向未破壞的部位傳播；當(dāng)載荷達(dá)到最大值9.66 kN時(shí)，基體破壞已經(jīng)擴(kuò)展至層壓板端部的另一邊緣；計(jì)算結(jié)束時(shí)，基體破壞和纖維破壞已經(jīng)擴(kuò)展到試驗(yàn)件的中部，此時(shí)的層壓板已完全失去承載能力.

4 結(jié)論

通過(guò)對(duì)[0]8、[15]20、[30]20、[45]20、[60]20、[80]20和[90]16共7種鋪層進(jìn)行偏軸拉伸試驗(yàn)，獲得了相應(yīng)的應(yīng)力-應(yīng)變曲線及拉伸強(qiáng)度.對(duì)不同鋪層角度的斷裂面角度進(jìn)行測(cè)量，測(cè)得的斷裂面角度與鋪層角度的差異在 -1°～2°之間，對(duì)斷裂面的觀察和分析表明導(dǎo)致此差異的原因?yàn)锳S4/PEEK層壓板在制造過(guò)程中鋪層角度和設(shè)計(jì)角度存在誤差.

對(duì)于AS4/PEEK層壓板在加載過(guò)程中表現(xiàn)出顯著的非線性力學(xué)行為和破壞行為，提出一個(gè)同時(shí)考慮塑性效應(yīng)和損傷累計(jì)的三維彈塑性損傷本構(gòu)模型，并開(kāi)發(fā)了基于Abaqus的用戶材料子程序VUMAT.塑性模型中的參數(shù)使用信任域反射算法計(jì)算得到，其值為a66=1.50，β=292.67和n=0.134 6.

將三維彈塑性損傷本構(gòu)模型應(yīng)用于單向AS4/PEEK層壓板的偏軸拉伸數(shù)值模擬，預(yù)測(cè)得到的應(yīng)力-應(yīng)變曲線與試驗(yàn)獲得的應(yīng)力-應(yīng)變曲線吻合良好，表明該模型能夠較為準(zhǔn)確地模擬單向AS4/PEEK層壓板的塑性效應(yīng).對(duì)加載過(guò)程中的各方向的塑性應(yīng)變的分析表明，1-2平面內(nèi)的剪切塑性應(yīng)變?cè)谒苄宰冃沃姓贾鲗?dǎo)地位.對(duì)比數(shù)值模擬與試驗(yàn)測(cè)量的拉伸強(qiáng)度，在相同的厚度下，隨著偏軸角度的增大，拉伸強(qiáng)度逐漸下降，預(yù)測(cè)的拉伸強(qiáng)度與實(shí)際的拉伸強(qiáng)度的最大誤差不超過(guò)20%，表明該模型適用于預(yù)測(cè)單向AS4/PEEK層合板的偏軸拉伸強(qiáng)度.