聲子晶體中低頻減振降噪技術(shù)及帶隙特性研究

胡啟國(guó)，白 熊，魏 晨，汪柯宇

(重慶交通大學(xué) 機(jī)電與車(chē)輛工程學(xué)院，重慶 400074)

0 引言

大型機(jī)械裝備產(chǎn)生的振動(dòng)噪聲往往呈現(xiàn)中低頻特性，這種噪聲更加沉悶，難以降噪，而聲子晶體技術(shù)因其特定頻段帶隙可設(shè)計(jì)性的特點(diǎn)，為齒輪箱減振降噪提供新的選擇.聲子晶體作為近年來(lái)用于裝備減振降噪研究新熱點(diǎn)，已被廣泛應(yīng)用于國(guó)防、航天、船舶、交通以及微電子領(lǐng)域.

早在二十世紀(jì)八十年代，就有學(xué)者提出一種具有特殊帶隙特性的功能材料，并將其命名為光子晶體[1,2].到了新世紀(jì)，學(xué)者在對(duì)周期變化的多材料復(fù)合結(jié)構(gòu)進(jìn)行研究時(shí)，發(fā)現(xiàn)彈性波在這些復(fù)合結(jié)構(gòu)中傳播時(shí)，周期結(jié)構(gòu)內(nèi)部形成獨(dú)特的色散關(guān)系[3,4]，故此聲子晶體的概念得以產(chǎn)生.聲子晶體結(jié)構(gòu)因?yàn)閷?duì)彈性波的帶隙特性而被廣泛運(yùn)用于機(jī)械行業(yè)中[5]，更因其輕質(zhì)、吸能、吸聲以及電磁屏蔽的特性，被現(xiàn)代工業(yè)認(rèn)為是當(dāng)前國(guó)際上最具前景的新一代先進(jìn)超材料[6].聲子晶體一般由兩種及兩種以上材料組合而成，材料組成十分豐富.

經(jīng)過(guò)學(xué)者們多年的研究，越來(lái)越多材料被用于聲子晶體的設(shè)計(jì).張賽等[7]選用石英玻璃和水作為一維聲子晶體結(jié)構(gòu)組成材料.Hyasse等[8]利用石墨烯-雙層半導(dǎo)體制備無(wú)限和半無(wú)限超晶格.聲子晶體帶隙特性除了與其組成材料有關(guān)外，還會(huì)受到不同結(jié)構(gòu)形狀的影響.考慮不同的應(yīng)用場(chǎng)景，學(xué)者們開(kāi)發(fā)出多種結(jié)構(gòu)形式的聲子晶體，并針對(duì)結(jié)構(gòu)參數(shù)對(duì)帶隙影響展開(kāi)分析.如李夏臨等[9]設(shè)計(jì)了一種二維分布式陀螺結(jié)構(gòu)聲子晶體.對(duì)晶格常數(shù)、散射體尺寸和陀螺式聲子晶體的角動(dòng)量、轉(zhuǎn)動(dòng)慣量和扭轉(zhuǎn)剛度對(duì)帶隙特性影響進(jìn)行了分析.康太鳳等[10]設(shè)計(jì)了一種空心散射體聲子晶體.這種聲子晶體由四個(gè)環(huán)氧樹(shù)脂連接板與空心鉛柱組合而成，其中鉛柱上附著硅橡膠材料.

考慮應(yīng)用場(chǎng)景不同，學(xué)者們針對(duì)不同應(yīng)用場(chǎng)景對(duì)聲子晶體進(jìn)行了設(shè)計(jì)與研究.許祥曦[11]將桁架管設(shè)計(jì)為一維聲子晶體周期性排列結(jié)構(gòu)形式，用于海洋平臺(tái)桁架減振系統(tǒng).Sheikhaleh等[12]利用二維光子晶體加壓濾波，基于波長(zhǎng)調(diào)制方法，提出了一種新型光學(xué)微機(jī)電系統(tǒng)加速度計(jì)傳感器.沈惠杰[13]將海水運(yùn)輸管路的振動(dòng)噪聲控制理論與聲子晶體帶隙特性相結(jié)合，基于一維聲子晶體結(jié)構(gòu)形式設(shè)計(jì)出周期性海水管路，使得海水運(yùn)輸管路具有水力噪聲帶隙特性.

基于現(xiàn)有研究基礎(chǔ)，考慮大型機(jī)械裝備，如大型齒輪箱中低頻振動(dòng)噪聲問(wèn)題，設(shè)計(jì)了一款包覆魔方型聲子晶體結(jié)構(gòu)，并對(duì)該聲子晶體帶隙產(chǎn)生機(jī)理，帶隙影響因素，傳輸損耗進(jìn)行了分析.

1 聲子晶體基本理論與結(jié)構(gòu)介紹

1.1 彈性波波動(dòng)方程

固體介質(zhì)中的某一點(diǎn)受到外界物理作用擾動(dòng)的情況下，由于介質(zhì)的彈性，會(huì)使得擾動(dòng)質(zhì)點(diǎn)同其周?chē)|(zhì)點(diǎn)間的彈性力增加.而這種質(zhì)點(diǎn)的作用持續(xù)下去，便會(huì)形成從擾動(dòng)源開(kāi)始的波動(dòng)現(xiàn)象.這種現(xiàn)象可以用彈性波波動(dòng)方程來(lái)進(jìn)行表示：

(1)

式(1)中：ρ為介質(zhì)密度，u為位移矢量，λ、μ都為L(zhǎng)ame系數(shù).而基于Lame定理和Helmholtz證明可以知道，對(duì)于任意矢量，在其定義域內(nèi)有散度存在，則該矢量便可以用一個(gè)標(biāo)量φ的梯度φ和一個(gè)矢量位Ψ的旋度×Ψ之和來(lái)表示，而彈性波動(dòng)場(chǎng)正好滿(mǎn)足這一條件，因此可以得到：

u=φ+×ψ

(2)

將式(2)代入式(1)中，并進(jìn)行散度與旋度變換可以得到φ和ψ滿(mǎn)足的波動(dòng)方程：

(3)

(4)

1.2 Bloch定理

(5)

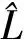
Yk,n(X)=eik×Xuk,n(X)

(6)

式(6)對(duì)應(yīng)其本征值滿(mǎn)足：

λk,n=λk+Gm,n

(7)

uk,n(X)對(duì)于格矢Rn的平移具有周期性質(zhì)，同樣滿(mǎn)足式：

uk,n(X+Rn)=uk,n(X)

(8)

(9)

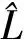
(10)

λk,n=λξk,n

(11)

由式(10)、(11)可以證明，波矢取值在倒格子空間高對(duì)稱(chēng)點(diǎn)處，本征場(chǎng)群沿對(duì)稱(chēng)面的法向分量取零，本征譜取極值.由此可知，如果想要計(jì)算帶隙頻率范圍而進(jìn)行能帶結(jié)構(gòu)計(jì)算，任意波矢k只要在不可約布里淵區(qū)的邊界取值開(kāi)展計(jì)算即可，其中不可約布里淵區(qū)如圖1中藍(lán)色部分所示.

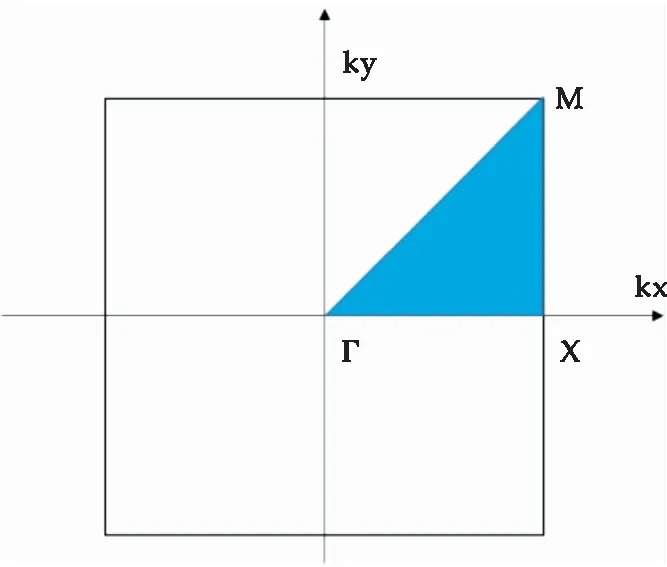
圖1 不可約布里淵區(qū)示意

1.3 包覆魔方型聲子晶體模型

考慮中、低頻段噪聲更加沉悶且難以降噪的特點(diǎn)，設(shè)計(jì)了一種包覆魔方型聲子晶體結(jié)構(gòu)，如圖2所示，該聲子晶體單胞結(jié)構(gòu)由兩種材料構(gòu)成，整個(gè)聲子晶體單胞為立方體結(jié)構(gòu)，各邊邊長(zhǎng)相等.同樣內(nèi)部散射體也為立方體結(jié)構(gòu)，由27個(gè)小立方體構(gòu)成一個(gè)類(lèi)似魔方的立方體結(jié)構(gòu).聲子晶體單胞外層包覆層由硅橡膠構(gòu)成，中心由金屬組成散射體，構(gòu)成一種可在中低頻范圍對(duì)彈性波進(jìn)行耗散的局域共振型聲子晶體單胞.

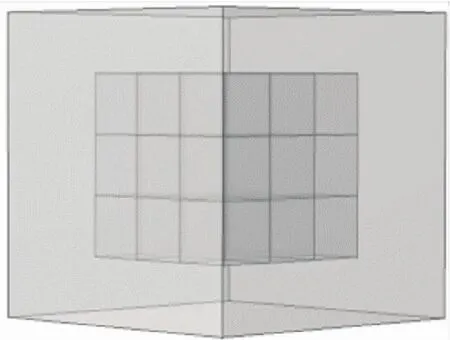
圖2 聲子晶體單胞結(jié)構(gòu)

2 聲子晶體帶隙產(chǎn)生機(jī)理分析

2.1 聲子晶體帶隙計(jì)算

基于有限元方法，利用Comsol分析軟件對(duì)包覆魔方型聲子晶體帶隙進(jìn)行求解.以晶格常數(shù)a為15 mm，散射體尺寸b為9 mm，其中散射體選用鎢材料，包覆層選用硅橡膠材料，材料參數(shù)如表1所示，對(duì)其帶隙進(jìn)行求解.

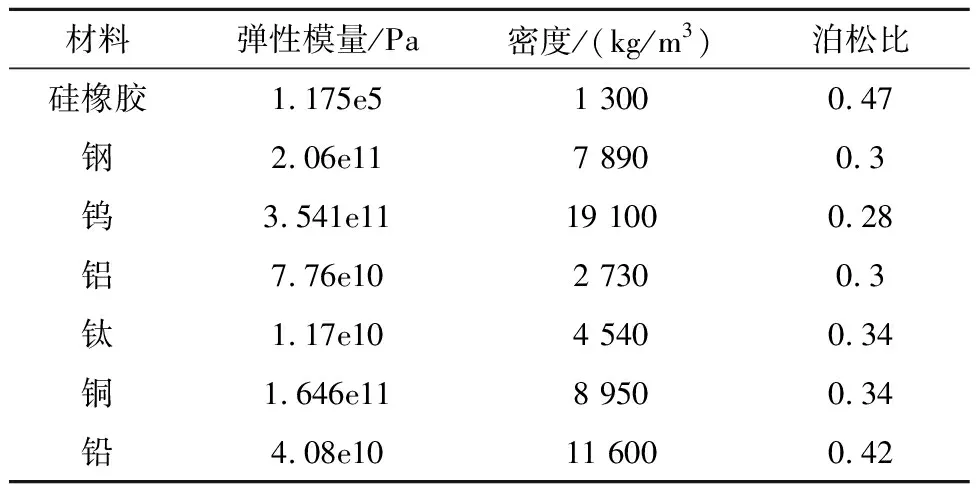
表1 材料參數(shù)表

首先，在幾何模塊中進(jìn)行建模，并利用材料模塊分別對(duì)包覆層與散射體進(jìn)行材料定義.接著添加固體力學(xué)物理場(chǎng)，并設(shè)置周期性邊界條件.由于該聲子晶體為立方結(jié)構(gòu)，彈性波從6個(gè)面入射，起到耗散彈性波效果相同，因此只對(duì)單獨(dú)一個(gè)面設(shè)置邊界條件.選擇周期性邊界條件類(lèi)型為Floquet周期，設(shè)置周期矢量kx，ky.最后設(shè)置參數(shù)化掃描，分別從Γ～X(0～π)，X～M(π～2π)，M～Γ(2π～3π)三個(gè)矢量方向?qū)哆M(jìn)行掃描，選取了10個(gè)特征頻率數(shù)量，通過(guò)軟件對(duì)聲子晶體特征頻率進(jìn)行求解，結(jié)合軟件自帶的參數(shù)化掃描功能，即可得到以鎢材料為散射體的包覆魔方型聲子晶體帶隙圖，如圖3所示.

從圖3可以看出，能帶在高對(duì)稱(chēng)點(diǎn)分開(kāi)，這是由于長(zhǎng)波行波在中低頻范圍內(nèi)，其波長(zhǎng)遠(yuǎn)遠(yuǎn)大于單元結(jié)構(gòu)也即晶格常數(shù)的長(zhǎng)度，而彈性波在中低頻范圍內(nèi)傳播與均勻介質(zhì)相同，能帶圖呈線(xiàn)性關(guān)系.當(dāng)硅橡膠包覆層中的行波頻率接近或者等于散射體共振單元的固有頻率時(shí)，則散射體共振單元內(nèi)會(huì)發(fā)生局域共振.硅橡膠包覆層中的長(zhǎng)波與散射體的共振模態(tài)相互耦合，絕大部分彈性波能量將被局域在散射體共振單元中，以此實(shí)現(xiàn)彈性屏蔽，故此會(huì)出現(xiàn)帶隙.以鎢材料為散射體，硅橡膠為包覆層的聲子晶體在166～350 Hz頻率范圍內(nèi)產(chǎn)生了完全帶隙，如圖陰影部分所示

圖3 鎢散射體帶隙結(jié)構(gòu)圖

2.2 高對(duì)稱(chēng)點(diǎn)振動(dòng)模態(tài)與帶隙產(chǎn)生機(jī)理

這里可以將聲子晶體等效為質(zhì)量-彈簧系統(tǒng)，如圖4所示，當(dāng)入射彈性波頻率處于完全帶隙頻段內(nèi)時(shí)，入射彈性波會(huì)對(duì)硅橡膠包覆層產(chǎn)生力F的作用，當(dāng)彈性波傳遞到振子Me而使其發(fā)生運(yùn)動(dòng)，振子Me同樣會(huì)對(duì)硅橡膠包覆層產(chǎn)生反作用力f.基體在兩力共同作用下振動(dòng)，當(dāng)入射彈性波激勵(lì)頻率與共振單元的固有頻率接近時(shí)，兩作用力反向疊加，包覆層合外力為零.因而包覆層趨于靜止?fàn)顟B(tài)，入射彈性波被局域化，振動(dòng)能量無(wú)法傳播，僅局限于共振單元中，能量被共振單元消耗掉，故而彈性波在完全帶隙頻段無(wú)法傳播.

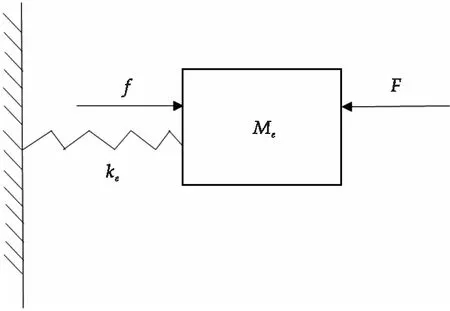
圖4 等效彈簧-質(zhì)量系統(tǒng)

基于聲子晶體等效質(zhì)量-彈簧系統(tǒng)，并對(duì)第一布里淵區(qū)內(nèi)的A～F六個(gè)高對(duì)稱(chēng)點(diǎn)的振動(dòng)模態(tài)進(jìn)行求解，對(duì)聲子晶體帶隙產(chǎn)生機(jī)理進(jìn)行分析，求解結(jié)果如圖5所示.其中A、B為彎曲振動(dòng)模式，A點(diǎn)的頻率為78.15 Hz，以y為軸發(fā)生彎曲，B點(diǎn)的頻率為89.83 Hz，以z軸為中心發(fā)生彎曲.此時(shí)該局域共振單元振子為硅橡膠包覆層，基體為散射體.散射體受到兩側(cè)硅橡膠包覆層的擠壓作用，分別z軸正向和y軸正向的移動(dòng).當(dāng)彈性波頻率和該局域共振系統(tǒng)固有頻率相似，散射體在發(fā)生位移后，處于靜止?fàn)顟B(tài)，此時(shí)聲子晶體原胞所受合力為零，故不能產(chǎn)生局域共振而耗散彈性波或者聲波.

圖5 A～F振型圖

C～F四個(gè)高對(duì)稱(chēng)點(diǎn)都為扭轉(zhuǎn)振動(dòng)模式，C點(diǎn)處的頻率為141.02 Hz，在該處聲子晶體原胞以y軸中心發(fā)生扭轉(zhuǎn)；D、E兩點(diǎn)處的頻率分別為164.92 Hz、184.62 Hz，都以z軸為中心進(jìn)行扭轉(zhuǎn)；F點(diǎn)處的頻率為347.74 Hz，以x軸為中心進(jìn)行扭轉(zhuǎn).C、F點(diǎn)處，共振單元振子為散射體，硅橡膠包覆層為基體，C、F點(diǎn)處分別以y、x為軸發(fā)生扭轉(zhuǎn)，扭轉(zhuǎn)帶動(dòng)散射體同時(shí)發(fā)生扭轉(zhuǎn)，當(dāng)入射彈性波剛好為這一頻率時(shí)，激發(fā)扭轉(zhuǎn)發(fā)生，此時(shí)散射體合力為0，故處于相對(duì)靜止?fàn)顟B(tài)，難以產(chǎn)生耗散彈性波的作用.D、E兩點(diǎn)處頻率時(shí)，入射彈性波與兩者頻率相同時(shí)，同樣激發(fā)扭轉(zhuǎn)發(fā)生，但入射頻率由于波長(zhǎng)的緣故，只激發(fā)了外部硅橡膠包覆層處的發(fā)生扭轉(zhuǎn)，而散射體相對(duì)靜止，故同樣不能起到耗散彈性波的作用.

3 聲子晶體帶隙特性影響分析

3.1 材料參數(shù)對(duì)帶隙特性的影響

對(duì)于聲子晶體，可以把帶隙特性影響因素分為兩類(lèi)，分別為材料參數(shù)和結(jié)構(gòu)尺寸因素[14,15].現(xiàn)在先從材料因素對(duì)包覆魔方型聲子晶體進(jìn)行分析.根據(jù)表1數(shù)據(jù)，選用鋼、鎢、鋁、鈦、銅、鉛分別作為散射體，得出不同材料下聲子晶體完全帶隙對(duì)比情況，如圖6所示.

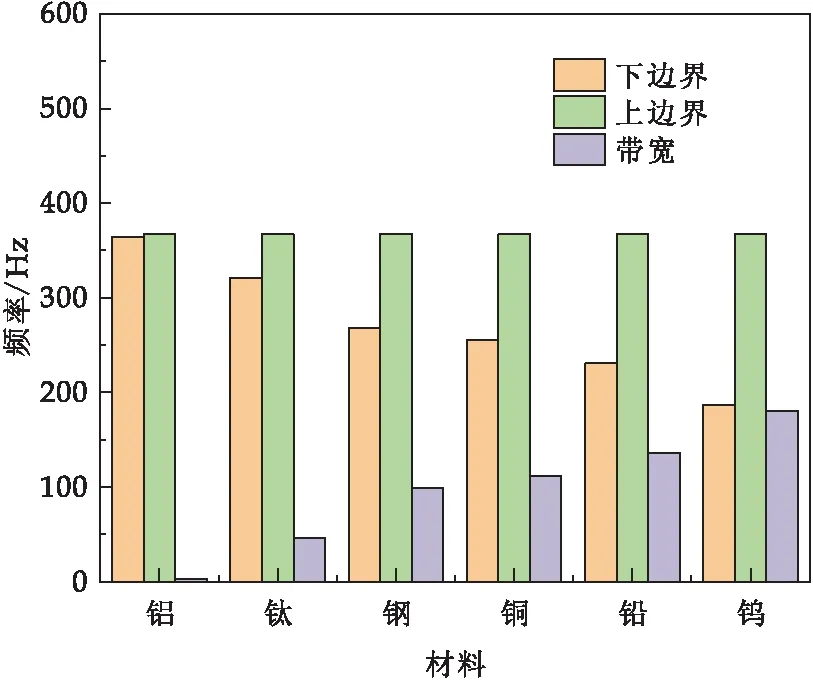
圖6 不同材料散射體聲子晶體完全帶隙對(duì)比

從圖6可以看出，包覆魔方型聲子晶體的完全帶隙寬度以鎢為散射體時(shí)最寬，鋁為散射體時(shí)完全帶隙寬度最小.并且，不同材料完全帶隙上邊界幾乎相同，而完全帶隙下邊界存在較大的差異.結(jié)合表1材料參數(shù)數(shù)據(jù)，發(fā)現(xiàn)鎢材料的彈性模量與密度皆高于其余材料，可以猜想該聲子晶體的完全帶隙寬度與材料彈性模量和密度間存在一定關(guān)系.為了驗(yàn)證這個(gè)猜想，選取以鎢為散射體的包覆魔方型聲子晶體，開(kāi)展材料力學(xué)參數(shù)對(duì)完全帶隙寬度影響分析，其結(jié)果如圖7、圖8所示.

由圖7可知，橫坐標(biāo)為楊氏模量，隨著楊氏模量的增加，聲子晶體帶隙上、下邊界幾乎保持不變，固可知楊氏模量對(duì)該聲子晶體帶隙影響效果并不明顯；由圖8可知，橫坐標(biāo)為包覆魔方型聲子晶體散射體質(zhì)量密度，隨著散射體質(zhì)量密度的增加，完全帶隙上、下邊界都處于減少趨勢(shì)，并且?guī)捲鰧?故此可以得出結(jié)論，聲子晶體散射體質(zhì)量密度對(duì)完全帶隙有一定影響，但影響范圍不大.

圖7 散射體楊氏模量對(duì)帶隙的影響

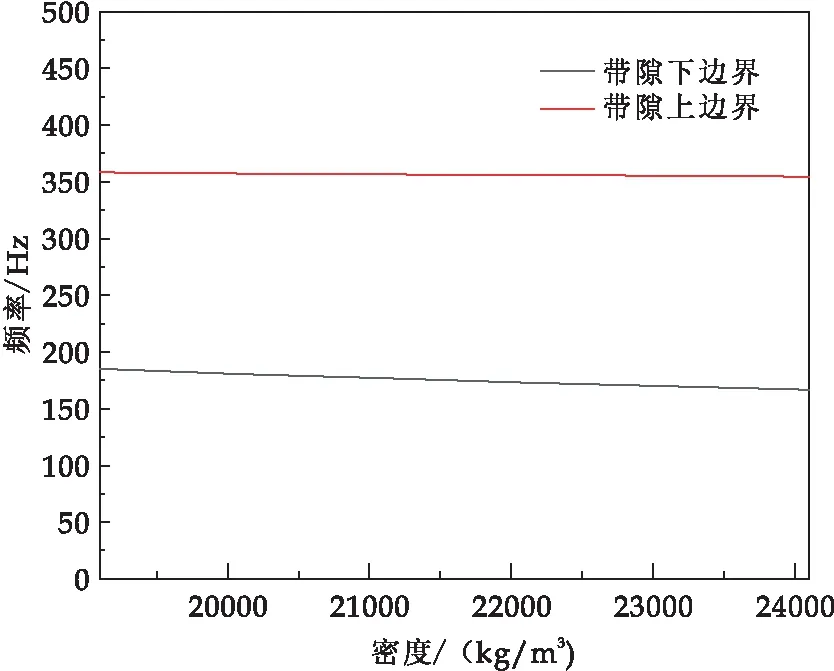
圖8 散射體密度對(duì)帶隙的影響

3.2 結(jié)構(gòu)參數(shù)對(duì)帶隙特性的影響

除了散射體材料對(duì)完全帶隙有影響外，聲子晶體自身結(jié)構(gòu)參數(shù)也會(huì)對(duì)完全帶隙造成影響.這里選取鎢材料作為包覆魔方型聲子晶體的散射體，分別以該包覆魔方型聲子晶體晶格常數(shù)、散射體尺寸為變量展開(kāi)分析，得出結(jié)論如圖9、圖10所示.

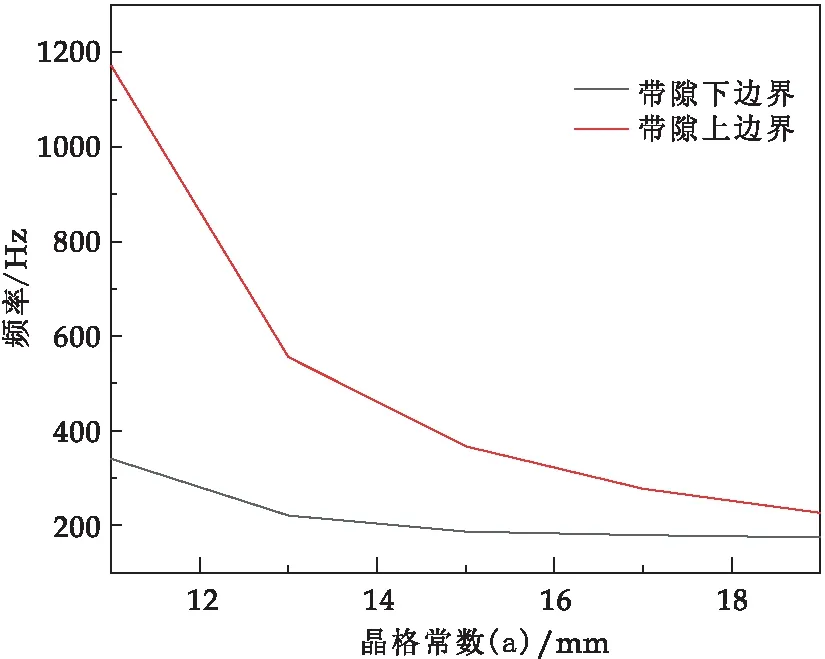
圖9 不同晶格常數(shù)對(duì)帶隙的影響

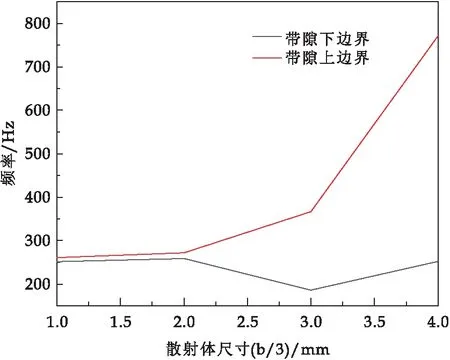
圖10 不同散射體尺寸對(duì)帶隙影響

圖9表示不同晶格常數(shù)下聲子晶體完全帶隙變化情況，隨著晶格常數(shù)的增加，完全帶隙上、下邊界呈減小趨勢(shì).上、下邊界對(duì)比可以得出，上邊界隨著晶格常數(shù)的增加，數(shù)值下降趨勢(shì)更加陡峭，而下邊界數(shù)值，相對(duì)更加平緩.圖10為散射體尺寸對(duì)完全帶隙影響曲線(xiàn)，包覆魔方型聲子晶體完全帶隙寬度隨著散射體邊長(zhǎng)的增加而增加，其中聲子晶體隨著散射體尺寸的增加，完全帶隙上邊界呈逐漸增加的趨勢(shì).隨著散射體尺寸的增加，完全帶隙下邊界呈先減少再增加的變化，其中增加轉(zhuǎn)折點(diǎn)出現(xiàn)在散射體尺寸為3 mm時(shí).從對(duì)比分析可知晶格常數(shù)和散射體尺寸都對(duì)完全帶隙有著顯著影響.

4 聲子晶體彈性波傳輸損耗分析

4.1 聲子晶體板振動(dòng)響應(yīng)

為了進(jìn)一步確定該包覆魔方型聲子晶體完全帶隙特性，選擇晶格常數(shù)a為15 mm，散射體尺寸b為9 mm，散射體為鎢，包覆層選用硅橡膠，驗(yàn)證包覆魔方型聲子晶體減振、降噪能力性能.利用Comsol多物理場(chǎng)分析軟件，首先對(duì)包覆魔方型聲子晶體板進(jìn)行建模，以聲子晶體單胞為基礎(chǔ)，利用陣列功能構(gòu)建10×10的聲子晶體板，同時(shí)在聲子晶體板兩側(cè)構(gòu)建過(guò)渡層與完美匹配層，如圖11所示.

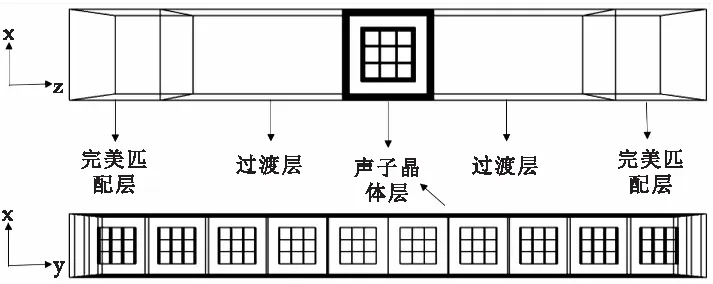
圖11 聲子晶體板傳輸損耗仿真模型

通過(guò)向z軸正方向給定振動(dòng)加速度1 m/s2，對(duì)傳輸損耗模型進(jìn)行求解，可以得到彈性波影響下聲子晶體內(nèi)部振動(dòng)位移云圖，如圖12所示.這里選擇141 Hz，251 Hz，301 Hz，521 Hz四個(gè)激勵(lì)頻率，當(dāng)激勵(lì)頻率落于聲子晶體完全帶隙頻段范圍以?xún)?nèi)時(shí)，彈性波受到聲子晶體局域共振的作用，使得彈性波被抑制，反之彈性波則可以順利通過(guò)聲子晶體.

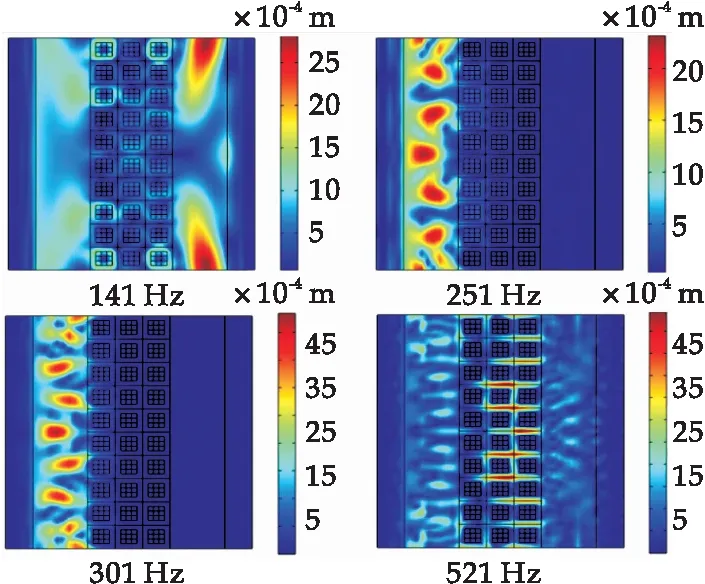
圖12 各激勵(lì)頻率下振動(dòng)位移云圖

4.2 不同層數(shù)聲子晶體板傳輸損耗對(duì)比

對(duì)于實(shí)際工程應(yīng)用中，由于現(xiàn)場(chǎng)環(huán)境的不同，聲子晶體減振、降噪的能力同樣也會(huì)有所差異[16].為了增強(qiáng)減振、降噪的能力，往往需要使用多層聲子晶體結(jié)構(gòu).為了了解不同層數(shù)聲子晶體的減振、降噪能力，這里提取了不同層數(shù)聲子晶體傳輸損耗曲線(xiàn)，如圖13所示.

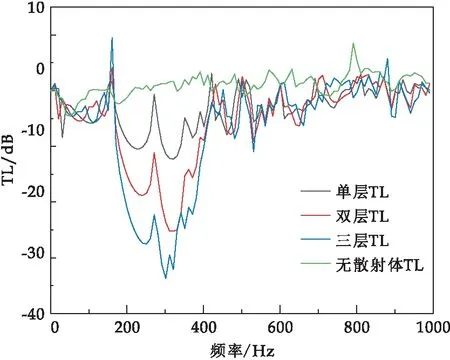
圖13 不同層數(shù)聲子晶體傳輸損耗對(duì)比

由圖13可以看出，橫坐標(biāo)為頻率，縱坐標(biāo)為傳輸損耗TL(Transmission Loss，TL)，在166～350 Hz頻段，隨著包覆魔方型聲子晶體板層數(shù)的增加，其傳輸損耗以每層10～15 dB數(shù)值減少.相比較于無(wú)散射體的硅橡膠板，其傳輸損耗效果明顯減少.但在160 Hz左右頻率范圍內(nèi)，隨著層數(shù)的增加，出現(xiàn)傳輸損耗數(shù)值的增加的現(xiàn)象.這是由于隨著層數(shù)的增加，在150 Hz頻率左右，聲子晶體降噪板和入射彈性波產(chǎn)生整體共振的原因.為了解決這一問(wèn)題，并優(yōu)化包覆魔方型聲子晶體板的減振效果，引入缺陷型聲子晶體板，利用聲子晶體板缺陷效應(yīng)來(lái)解決這一問(wèn)題.

4.3 不同缺陷聲子晶體傳輸損耗對(duì)比

所謂聲子晶體缺陷，就是在周期排列的聲子晶體中出現(xiàn)一點(diǎn)、一條線(xiàn)和一個(gè)面的異于其它聲子晶體的結(jié)構(gòu)形式，在帶隙圖上表現(xiàn)出來(lái)就是會(huì)在其它頻段產(chǎn)生完全帶隙的現(xiàn)象.這里選用三層聲子晶體板，在中間層設(shè)置聲子晶體散射體尺寸缺陷、聲子晶體散射體材料缺陷兩種缺陷形式，得出傳輸損耗曲線(xiàn)如圖14、圖15所示.

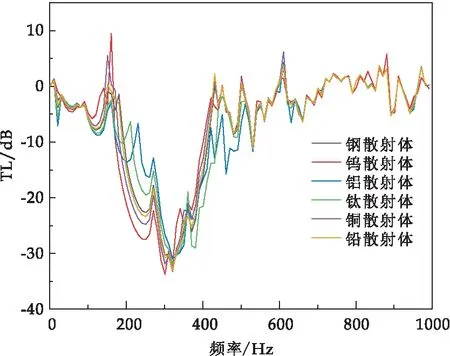
圖15 不同散射體材料缺陷傳輸損耗對(duì)比

從圖14可以看出，中間缺陷層聲子晶體散射體尺寸b為9 mm和b為7 mm時(shí)，在頻率170 Hz左右產(chǎn)生傳輸損耗增加的現(xiàn)象，也即出現(xiàn)傳輸損耗異常，當(dāng)使用這兩種聲子晶體降噪板時(shí)，在165 Hz頻率附近將導(dǎo)致彈性波的增大，也即振動(dòng)幅度增大.此外，在使用缺陷型聲子晶體板后，在頻段60～155 Hz范圍內(nèi)，相較于無(wú)缺陷聲子晶體板，產(chǎn)生了新的完全帶隙.散射體尺寸b不同時(shí)，產(chǎn)生帶隙值不同，當(dāng)b為11 mm時(shí)，產(chǎn)生的最大傳輸損耗為16.5 dB.通過(guò)引入散射體尺寸點(diǎn)缺陷聲子晶體單胞，可以有效優(yōu)化聲子晶體彈性波傳輸損耗異常增加現(xiàn)象，從而提升聲子晶體板減振、降噪性能.

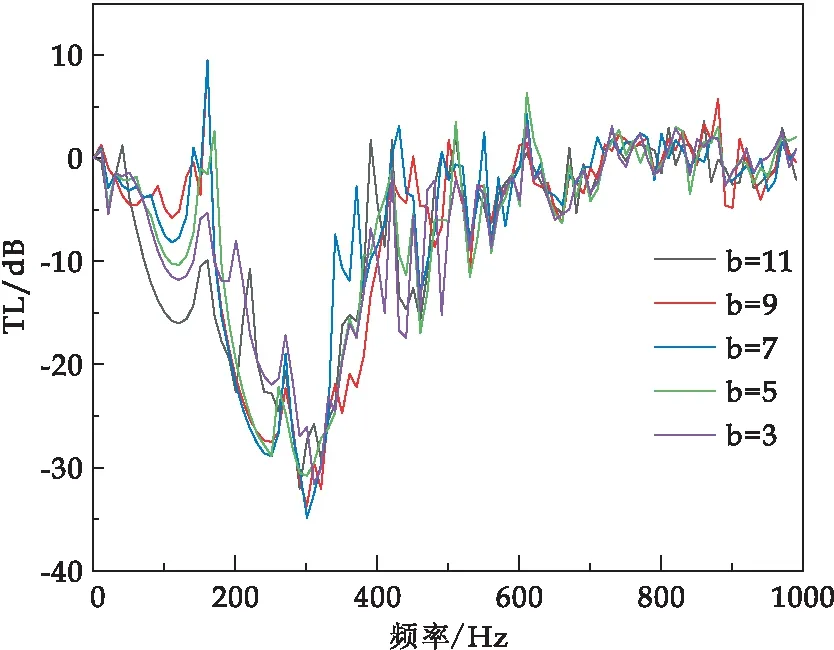
圖14 不同散射體尺寸缺陷傳輸損耗對(duì)比

由圖15可以看出，當(dāng)缺陷層散射體材料為鎢和鉛時(shí)，165 Hz附近傳輸損耗增加.引入鉛作為散射體的缺陷聲子晶體也出現(xiàn)與無(wú)缺陷聲子晶體一樣的問(wèn)題，這是由于鉛的力學(xué)性質(zhì)，如密度、彈性模量，相較于其它材料更加接近如鎢，故此會(huì)產(chǎn)生近似的帶隙特性.在頻率166～350 Hz范圍內(nèi)，也即鎢材料包覆魔方聲子晶體完全帶隙頻段范圍內(nèi)，無(wú)缺陷聲子晶體傳輸損耗特性表現(xiàn)最佳，隨后依次為鉛、銅、鋼、鈦、鋁作為散射體的聲子晶體單胞.然而在92～160 Hz范圍內(nèi)，傳輸損耗效果最佳的為鋁材料，隨后依次為鈦、鋼、銅、鉛、鎢，并且以鋁、鈦、鋼、銅為散射體的缺陷聲子晶體單胞在這個(gè)頻段范圍內(nèi)未出現(xiàn)傳輸損耗增加的現(xiàn)象.為此可以得出結(jié)論在鎢材料為散射體的聲子晶體板中，引入不同材料作為散射體的缺陷聲子晶體單胞可以在其它頻段產(chǎn)生額外完全帶隙，基于這一規(guī)律，可以達(dá)到額外頻段的傳輸損耗優(yōu)化效果.

5 結(jié)論

(1)提出一種包覆魔方型聲子晶體結(jié)構(gòu)，以鎢為散射體材料，硅橡膠為包覆層，利用Comsol多物理場(chǎng)分析軟件，對(duì)帶隙進(jìn)行求解，發(fā)現(xiàn)在中低頻段(166～350 Hz)產(chǎn)生完全帶隙結(jié)構(gòu)；基于該聲子晶體對(duì)其帶隙產(chǎn)生機(jī)理進(jìn)行分析.

(2)從散射體材料參數(shù)和聲子晶體結(jié)構(gòu)參數(shù)對(duì)帶隙特性的影響進(jìn)行分析，得出結(jié)論：這些參數(shù)都對(duì)聲子晶體完全帶隙有著相應(yīng)的影響，其中晶格常數(shù)和散射體尺寸對(duì)帶隙影響更為明顯.

(3)為了驗(yàn)證聲子晶體減振降噪性能，搭建聲子晶體傳輸損耗求解模型，分析了不同層數(shù)聲子晶體傳輸損耗變化情況，發(fā)現(xiàn)每增加一層，聲子晶體傳輸損耗隨機(jī)減少約10～15 dB.

(4)為了解決隨著層數(shù)的增加，特定頻段傳輸損耗不降反升的問(wèn)題，利用散射體尺寸缺陷、散射體材料缺陷對(duì)傳輸損耗進(jìn)行優(yōu)化，通過(guò)引入缺陷聲子晶體解決了傳輸損耗異常的問(wèn)題，而且產(chǎn)生了新的完全帶隙，使得減振、降噪頻段得以擴(kuò)展.