密度泛函理論計算半導體材料的帶隙誤差研究

張澤群，孫慶德

(中國工程物理研究院 a. 北京計算科學研究中心，b. 研究生院，北京 100193)

電子能帶結構是材料最為關鍵的基本性質之一。從電子的能帶結構出發，根據電子的填充情況，可以區分導體、半導體和絕緣體。帶隙是半導體的電子能帶結構中最為重要的性質之一，定義為導帶的最小值(conduction band minimum，CBM)與價帶的最大值(valence band maximum, VBM)之間的差值，可以根據CBM和VBM對應的高對稱點是否相同分為直接帶隙與間接帶隙。能否較好地描述電子能帶結構是第一性原理計算研究領域的一項重要研究課題。

對于材料電子能帶結構的第一性原理描述，最常用的方法是基于局域密度近似(local density approximation, LDA)或廣義梯度近似(generalized gradient approximation, GGA)的Kohn-Sham密度泛函理論[1-3]，但是這個方法的不足是帶隙的計算值偏小。對于傳統的半導體材料，通過LDA或GGA法計算得到的帶隙值均要比實驗值小很多[4]，且有材料的帶隙越小，計算帶隙誤差越小的趨勢，因此有觀點認為當帶隙為0時，就會像金屬材料一樣，LDA或GGA方法計算的帶隙誤差會消失。針對上述觀點，本文中以半導體材料砷化鎵為例，對LDA或GGA法帶隙計算值的誤差問題進行研究，并在理論上給出出現帶隙誤差的物理解釋。

1 LDA或GGA法計算的帶隙誤差

LDA或GGA法可以在花費較少的計算資源的條件下得到材料體系較為準確的多種性質，但是這2種方法的主要缺點是會導致砷化鎵、單晶硅等傳統半導體的帶隙計算值顯著偏小。雜化泛函法是在LDA、GGA法的基礎上引入Hartree-Fock交換能而得到的一種計算方法，例如Heyd-Scuseria-Ernzerhof(HSE)方法，可以更精確地計算帶隙，但是相應的計算量和計算時長增加數倍。

采用不同方法得到的幾種常見半導體材料的帶隙計算值與實驗值如表1所示。可以看出，LDA、GGA法計算得到的帶隙的差別不明顯，均存在帶隙計算值偏小的現象，而HSE法計算得到的帶隙與實驗值較吻合，因此可以分別使用GGA、HSE法計算的帶隙值代表LDA、GGA法的計算值和實驗值。

表1 采用不同方法得到的不同材料的帶隙計算值與實驗值

對帶隙誤差進行進一步的分析，得到GGA法的帶隙誤差與帶隙實驗值之間的關系，如圖1所示。由圖可以看出，LDA、GGA法計算帶隙的誤差與材料本身的帶隙具有正相關的趨勢，即材料的帶隙越大，則LDA、GGA法計算的帶隙誤差也越大；帶隙越小，則LDA、GGA法計算的帶隙誤差也越小。對于金屬材料來說，LDA、GGA法計算得到的結果是正確的，因此有觀點認為，當半導體材料的帶隙為0時，就會像沒有帶隙的金屬材料一樣，LDA或GGA法計算的帶隙誤差也會消失。

圖1 采用廣義梯度近似方法計算得到的 不同半導體材料的帶隙誤差與帶隙實驗值

本文中以閃鋅礦構型(zincblende)的砷化鎵為例，通過對其進行加壓即壓縮晶格體積的方式來減小帶隙，分別利用GGA、HSE法進行計算，探究砷化鎵的帶隙為0時，LDA、GGA法計算的帶隙誤差是否消失。

2 計算方法

本文中所有的計算采用的是基于密度泛函理論的Vienna從頭計算模擬軟件包(Viennaabinitiosimulation package，VASP)[10]。在計算中使用了投影綴加平面波的方法來處理價電子與原子核之間的相互作用力[11]。體系的交換關聯泛函采用基于GGA的Perdew-Burke-Ernzerhof 交互關聯泛函(PBE)[12]法與雜化泛函HSE[13]法。對于所有的計算過程，設定平面波函數動能的截斷能為500 eV； 在結構馳豫的過程中，設定原子受力與能量的收斂判據分別為0.1 eV/nm和10-5eV。簡約布里淵區取尺寸為12×12×12(倒格矢a、b、c方向上高對稱點K點的數量)的K點網格。在使用HSE法時，設定引入Hartree-Fock精確交換能的比例系數為0.28。

3 結果與討論

通過對砷化鎵晶格進行應變工程來調控體系的帶隙，即通過施加外壓壓縮晶格體積的方式調控帶隙。在具體的計算過程中，采取等比例改變VASP的輸入文件POSCAR中基矢的縮放系數來實現，即從三維方向上同時等比例地壓縮晶格常數，相當于改變了原胞的體積。確定基矢的縮放系數取值區間為0.80～1.06、步長為0.01進行計算，與平衡狀態下的原胞相比，砷化鎵晶格的體積變化率為51.2%～119.1%。

對于所得計算數據，通過擬合Birch-Murnaghan(BM)固體狀態方程[14]，可以分別獲得砷化鎵晶體的體系總能量、壓強、體積彈性模量與晶格體積的關系，如圖2所示。BM固體狀態方程為

(1)

(2)

(3)

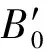
(a)總能量-晶格體積(b)壓強-晶格體積(c)體積彈性模量-晶格體積GGA-PBE—基于廣義梯度近似-Perdew-Burke-Ernzerhof 法; HSE—雜化泛函Heyd-Scuseria-Ernzerhof法。圖2 采用不同方法計算得到的砷化鎵晶體的體系總能量、壓強、體積彈性模量與晶格體積的關系

利用GGA-PBE、HSE法分別計算得到的晶格常數、帶隙等計算值與實驗值如表2所示。可以看出，GGA-PBE法計算得到的晶格常數偏大，而帶隙和體積彈性模量的計算值顯著偏小； HSE法的計算值與實驗值吻合較好。為了排除晶格常數的誤差對GGA-PBE法計算帶隙的影響，代入晶格常數實驗值，分別采用GGA-PBE、HSE法進行計算，發現GGA-PBE法計算得到的體積彈性模量與HSE法的相同，而帶隙計算值仍然偏小，說明晶格常數的差異不是引起帶隙誤差的主要原因。

表2 采用不同方法得到的砷化鎵晶格常數、體積彈性模量、帶隙的計算值與實驗值

在壓縮晶格體積的過程中采用GGA-PBE、HSE法計算得到的砷化鎵帶隙與晶格體積、壓強的關系如圖3所示，其中的紅色標點為平衡態的取值點。由圖可以看出，2種方法計算得到的帶隙均隨著晶格體積的壓縮經歷一個先增大后減小的過程，且會產生由直接帶隙半導體到間接帶隙半導體的轉換過程。

(a)晶格體積

(b)壓強 GGA-PBE—基于廣義梯度近似的Perdew-Burke-Ernzerhof 法；HSE—雜化泛函Heyd-Scuseria-Ernzerhof法。圖3 不同方法計算得到的砷化鎵帶隙與 晶格體積、壓強的關系

對砷化鎵轉為間接帶隙半導體的過程進行研究，在這一過程中，價帶最小值的取值點一直都在Γ點。選取砷化鎵電子結構的高對稱點Γ、X處的導帶能量值隨體積變化的關系進行研究，導帶最小值的取值點會隨著體積的壓縮從Γ點轉變到X點，由此產生了直接帶隙半導體到間接帶隙半導體的轉變。計算得到的砷化鎵導帶的Γ、X點與價帶Γ點之間的能量差值與晶格體積的關系如圖4所示，圖中標點處為對應2種方法的平衡態的取值點。

GGA-PBE—基于廣義梯度近似的Perdew-Burke-Ernzerhof 法；HSE—雜化泛函Heyd-Scuseria-Ernzerhof法。圖4 不同方法對應導帶的Γ、X點與價帶Γ點 之間的能量差值與晶格體積的關系

GGA-PBE、HSE法均顯示，隨著體積的壓縮，Γ點能量不斷增大； 隨著體積的壓縮，X點能量不斷減小，其原因是對于砷化鎵而言，Γ點的形變勢是正的，而X點的形變勢是負的。

對于間接帶隙減小過程，HSE法計算的帶隙誤差、GGA-PBE法計算的帶隙誤差與帶隙的關系如圖5所示。由圖可以看出，對于砷化鎵而言，帶隙越小，LDA或GGA法計算的帶隙誤差越小。

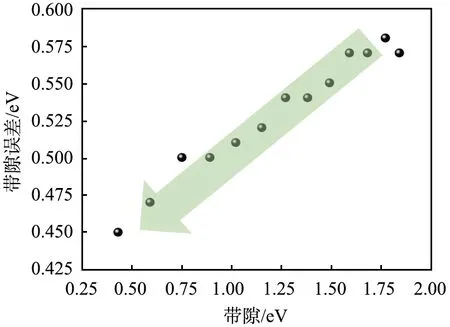
圖5 采用基于廣義梯度近似的Perdew-Burke-Ernzerhof 法計算的砷化鎵的帶隙誤差與帶隙的關系

進一步研究當半導體帶隙減小到0時，不同方法計算的帶隙誤差是否會消失。根據圖3，當采用GGA-PBE法，且晶格體積壓縮到27.36×10-3nm3時(對應的壓強為122 GPa)，LDA或GGA法計算的帶隙為0。當采用HSE法，體積壓縮到23.58×10-3nm3時(對應的壓強為190 GPa)，帶隙為0。兩者對比可以看出，當壓縮晶格體積使HSE法的計算的帶隙為0時，GGA法計算得到的帶隙并不等于0，反之亦然，因此當帶隙為0時，LDA或GGA法計算的帶隙誤差會消失這一說法是不準確的。

為了探究引起帶隙誤差的根源，通過HSE法計算得到砷化鎵在CBM、VBM處的波函數分布，如圖6所示。由圖可以看出，砷化鎵的VBM主要是由砷原子(As) 的p軌道組成的，而CBM主要是由鎵原子(Ga)的 s軌道組成的，這2個態的交換關聯勢之間存在差別，軌道波函數的不連續性是導致LDA、GGA法計算的帶隙偏小的主要原因。

圖6 砷化鎵的導帶的最小值與價帶的最大值處波函數的分布

對砷化鎵帶隙形成的物理過程進行理論分析，如圖7所示。VBM由As的p軌道和Ga的p軌道耦合得到，而CBM是由As的s軌道與Ga的s軌道耦合得到的，這種CBM與VBM處的s、p軌道波函數的不連續性與帶隙關系不大，因此GGA的計算帶隙誤差也與帶隙關系不大，即使帶隙為0，這個誤差仍然存在，這主要是由CBM和VBM的原子軌道組成決定的。

圖7 砷化鎵帶隙形成的物理過程

4 結論

針對LDA、GGA法導致帶隙計算值偏小的現象，本文中以砷化鎵為例研究計算帶隙誤差與帶隙的關系。結果表明，帶隙趨近于0時，LDA、GGA法計算的帶隙誤差逐漸減小，但是并不會消失。對于GaAs半導體來說，CBM和VBM處的波函數的不連續性是導致LDA、GGA法計算帶隙偏小的主要原因，而且這個計算誤差不會隨帶隙的消失而消失，因此需要研究一種新的方法來對半導體的帶隙進行更精準的計算，例如采用多體格林函數方法。