離散型隨機變量數字特征的常見題型及處理策略

郭興甫

(云南省曲靖市會澤縣東陸高級中學)

離散型隨機變量的數字特征是高中數學教材中的重要內容,也是每年高考命題的熱點內容,題目難度中等偏上,題型多以解答題的形式出現,分值在12至17分之間.為幫助各位讀者能在高考復習中更好地掌握這部分內容,本文以近年的高考及模擬題為例說明這部分內容的常見題型及處理策略,供復習參考.

1 離散型隨機變量分布列的性質及其應用

例1(1)若離散型隨機變量X的分布列為

(2)(多選題)已知m,n均為正數,隨機變量X的分布列如表1所示,則下列結論一定成立的是( ).

表1

A.P(X＝1)＜P(X≠1)

B.E(X)＝1

D.D(X＋1)＜1

綜上,選BCD.

2 求離散型隨機變量的分布列

例2已知2件次品和3件正品混放在一起,現需要通過檢測將其區分,每次隨機檢測一件產品,檢測后不放回,直到檢測出2件次品或者檢測出3件正品時檢測結束.

(1)求第一次檢測出的是次品且第二次檢測出的是正品的概率;

(2)已知每檢測一件產品需要費用100元,設X表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求X的分布列.

(2)X的可能取值為200,300,400,則

故X的分布列如表2所示.

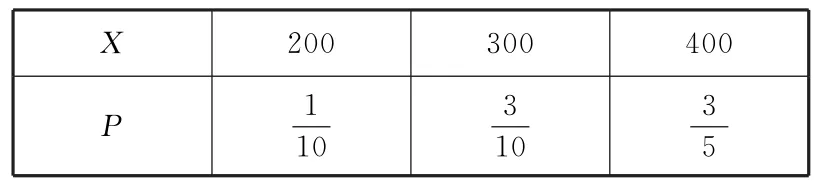
表2

3 求離散型隨機變量的均值與方差

例32022年世界乒乓球團體錦標賽于9 月30日至10月9日在成都舉行.近年來,乒乓球運動已成為國內民眾喜愛的運動之一.今有甲、乙兩位選手爭奪乒乓球比賽冠軍,比賽采用三局兩勝制,即某位選手率先獲得兩局勝利時比賽結束.根據以往經驗,甲、乙在一局比賽獲勝的概率分別為,且每局比賽結果相互獨立.

(1)求甲獲得乒乓球比賽冠軍的概率;

(2)比賽開始前,工作人員買來兩盒新球,分別為“裝有2個白球與1個黃球”的白盒與“裝有1個白球與2個黃球”的黃盒.每局比賽前裁判員從盒中隨機取出1個球用于比賽,且局中不換球,該局比賽后,直接丟棄.裁判按照如下規則取球:每局取球的盒子顏色與上一局比賽用球的顏色一致,且第一局從白盒中取球.記甲、乙決出冠軍后,兩盒內白球剩余的總數為X,求隨機變量X的分布列與數學期望.

記事件A:“甲奪得冠軍”,則

記Wi表示第i局從白盒中抽取的白色球,Yi表示第i局從黃盒中抽取的黃色球,X的所有可能取值為1,2,3,所以

綜上,X的分布列如表3所示.

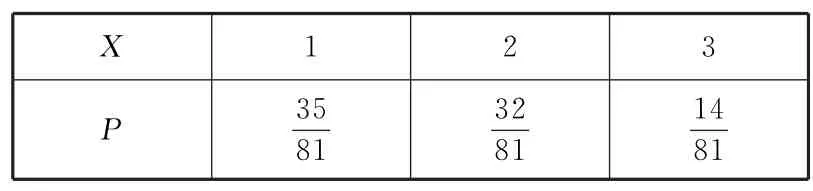
表3

例4教育部門出臺了“雙減”政策,即有效減輕義務教育階段學生過重作業負擔和校外培訓負擔,持續規范校外培訓(包括線上培訓和線下培訓).“雙減”政策的出臺對校外的培訓機構經濟效益產生了嚴重影響.某大型校外培訓機構為了規避風險,尋求發展制訂科學方案,工作人員對2022年前200名報名學員的消費金額進行了統計整理,其中數據如表4所示.

表4

(1)該大型校外培訓機構轉型方案之一是將文化科輔導培訓向音體美等興趣愛好培訓轉移.為了深入了解當前學生的興趣愛好,工作人員利用分層抽樣的方法在消費金額為[9,11)和[11,13)的學員中抽取了5人,再從這5人中選取3人進行有獎問卷調查,求抽取的3人中消費金額為[11,13)的人數的分布列和數學期望.

(2)以頻率估計概率,假設該大型校外培訓機構2022年所有學員的消費金額可視為服從正態分布N(μ,σ2),μ,σ2分別為前200名報名學員消費金額的平均數ˉx以及方差s2(同一區間的花費用區間的中點值替代).

(ⅰ)試估計該機構學員2022 年消費金額為[5.2,13.6)的概率(保留一位小數);

(ⅱ)若從該機構2022年所有學員中隨機抽取4人,記消費金額為[5.2,13.6)的人數為η,求η的方差.

X的分布列如表5所示.

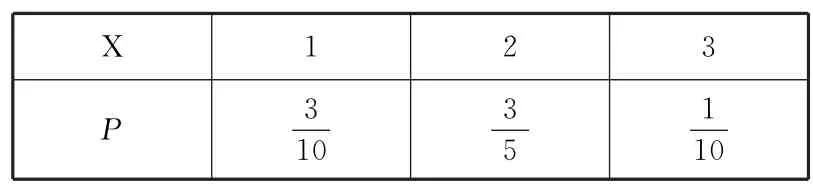
表5

(2)(ⅰ)由題意得

4 隨機變量均值與方差在決策中的應用

例5某公司圓滿完成預定的生產任務,為答謝員工的辛勤努力,公司決定在聯歡晚會后,擬通過摸球兌獎的方式對500位員工進行獎勵,規定:每位員工從一個裝有4種面值的獎券的箱子中,一次隨機摸出2張獎券,獎券上所標的面值之和就是該員工所獲得的獎勵額.

(1)若箱子中所裝的4種面值的獎券中有1張面值為80元,其余3張均為40元,試比較員工獲得80元獎勵額與獲得120元獎勵額的概率的大小;

(2)公司對獎勵總額的預算是6萬元,預定箱子中所裝的4種面值的獎券有兩種方案:第一種方案是2張面值20元和2張面值100元;第二種方案是2張面值40元和2張面值80元.為了使員工得到的獎勵總額盡可能地符合公司的預算且每位員工所獲得的獎勵額相對均衡,請問選擇哪一種方案比較好? 并說明理由.

所以P(X＝80)＝P(X＝120),故員工獲得80元獎勵額與獲得120元獎勵額的概率相等.

(2)第一種方案為(20,20,100,100),設員工所獲得的獎勵額為X1,則X1的可能取值為40,120,200,所以

所以X1分布列如表6所示.

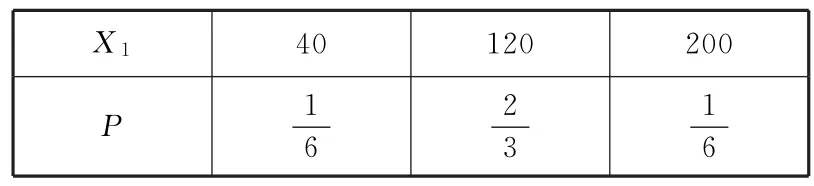
表6

第二種方案為(40,40,80,80),設員工所獲得的獎勵額為X2,則X2的分布列如表7所示.

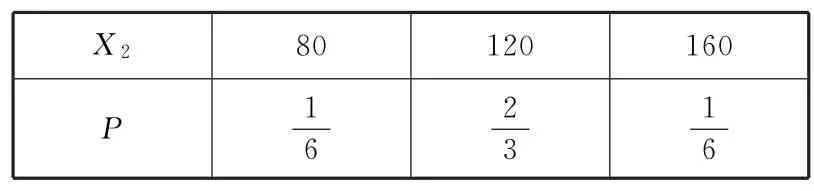
表7

又因為500E(X1)＝500E(X2)＝60000元,所以兩種方案獎勵額的數學期望都符合要求,但第二種方案的方差比第一種方案的小,故應選擇第二種方案.

例6在中國共產黨的正確領導下,我國順利實現了第一個百年奮斗目標——全面建成小康社會.某地為了鞏固扶貧成果,決定繼續對甲、乙兩家鄉鎮企業進行指導.指導方式有兩種,一種是精準指導,一種是綜合指導.已知對甲企業采用精準指導時,投資50萬元,增加100萬元收入的概率為0.2,增加200萬元收入的概率為0.8,采用綜合指導時,投資100萬元,增加200萬元收入的概率為0.6,增加400萬收入的概率為0.4;對乙企業采用精準指導時,投資50萬元,增加100萬元收入的概率為0.3,增加200萬元收入的概率為0.7,采用綜合指導時,投資100萬元,增加200萬元收入的概率為0.7,增加400萬元收入的概率為0.3.指導結果在兩家企業之間互不影響.

(1)若決策部門對甲企業進行精準指導、對乙企業進行綜合指導,設兩家企業增加的總收入為X萬元,求X的分布列;

(2)若有150萬元無息貸款可供甲、乙兩家企業使用,對兩家企業應分別進行哪種指導總收入最高?請說明理由.

故當決策部門對甲企業進行精準指導、對乙企業進行綜合指導時,兩家企業增加的總收入X的分布列如表8所示.

表8

(2)指導方案1:對甲、乙兩家企業均進行精準指導.設兩家企業增加的總收入為Y萬元,則Y的可能取值為200,300,400,且

指導方案2:對甲企業進行精準指導、對乙企業進行綜合指導.

由(1)可得E(X)＝300×0.14＋400×0.56＋500×0.06＋600×0.24＝440.

指導方案3:對甲企業進行綜合指導、對乙企業進行精準指導.

設兩家企業增加的總收入為Z,則Z的可能取值為300,400,500,600,且

因為350＜440＜450,故選擇指導方案3,即對甲企業進行綜合指導、對乙企業進行精準指導總收入最高.

5 分布列、均值與方差的創新應用

例7某汽車公司最近研發了一款新能源汽車,并在出廠前對100輛汽車進行了單次最大續航里程(理論上是指新能源汽車所裝載的燃料或電池所能夠提供給車行駛的最遠里程)的測試.現對測試數據進行分析,得到如圖1所示的頻率分布直方圖.

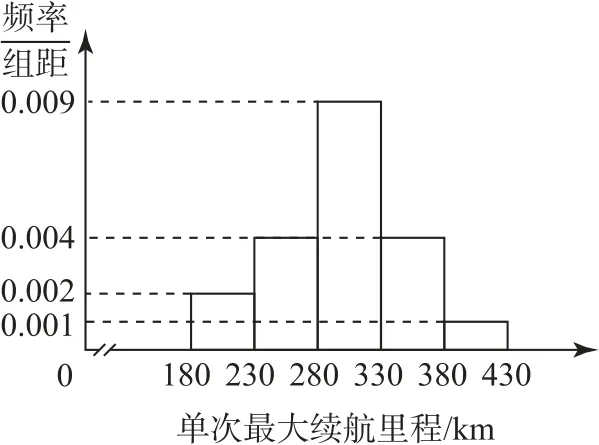
圖1

(1)估計這100輛汽車的單次最大續航里程的平均值xˉ(同一組中的數據用該組區間的中點值代表);

(2)根據大量的汽車測試數據,可以認為這款汽車的單次最大續航量程X近似地服從正態分布N(μ,σ2),經計算第(1)問中樣本標準差s的近似值為50.用樣本平均數作為μ的近似值,用樣本標準差s作為σ的估計值,現任取一輛汽車,求它的單次最大續航里程恰在250km 到400km 之間的概率;

(3)某汽車銷售公司為推廣此款新能源汽車,現面向意向客戶推出“玩游戲,送大獎”活動,客戶可根據拋擲硬幣的結果,操控微型遙控車在方格圖上行進,若遙控車最終停在“勝利大本營”,則可獲得購車優惠券.已知硬幣出現正、反面的概率都是,方格圖上標有第0格、第1格、第2格、…、第50格.遙控車開始在第0格,客戶每擲一次硬幣,遙控車向前移動一次,若擲出正面,遙控車向前移動一格(從k到k＋1),若擲出反面,遙控車向前移動兩格(從k到k＋2),直到遙控車移到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結束.設遙控車移到第n格的概率為Pn,試證明{Pn－Pn－1}(1≤n≤49,n∈N?)是等比數列,并解釋此方案能否成功吸引顧客購買該款新能源汽車.

參考數據:若隨機變量ξ服從正態分布N(μ,σ2),則

(2)由(1)及條件可得X～N(300,502),所以

(3)遙控車開始在第0格為必然事件,P0＝1,第一次擲硬幣出現正面,遙控車移到第一格,其概率為

遙控車移到第n(2≤n≤49)格有兩種可能:①遙控車先到第n－2格,又擲出反面,其概率為②遙控車先到第n－1 格,又擲出正面,其概率為,所以

鏈接練習

1.已知隨機變量X～B(6,p),Y～N(μ,σ2),且P(Y≥2)＝,E(X)＝E(Y),則p＝( ).

2.某圍棋學校選拔參加圍棋大賽選手的規則如下:①每位參加者都要依次和A,B,C,D四位大師進行四場比賽;②每場比賽參賽選手只有獲勝和失敗兩種結果,若獲勝,則該場比賽依次得1分,1分,1分,3分;若失敗,則該場得0分;③四場比賽結束后,累計得分大于或等于5分,則成為圍棋大賽選手;小于5分時,則不能成為圍棋大賽選手.學生甲和A,B,C,D四位大師進行比賽,獲勝的概率依次為,且各場比賽相互之間沒有影響.

(1)求學生甲成為圍棋大賽選手的概率;

(2)設學生甲最后累計得分為X,求X的分布列和數學期望.

鏈接練習參考答案

1.B.

(2)隨機變量X的分布列如表9所示.

表9

(完)