一道兩線段長乘積為定值月考題的背景與性質應用

北京市第十二中學高中部(100071) 劉剛

1.試題呈現

(1)求橢圓C的方程及A點坐標;

(2) 設直線l與x軸交于點B,過點B的直線與橢圓C交于E,F兩點,記A在x軸上的投影為G,T為BG的中點,直線AE,AF與x軸分別交于M,N兩點,試探究|TM|·|TN|是否為定值,若為定值,求出此定值;否則,請說明理由.

試題考查了橢圓的標準方程、幾何性質、直線與橢圓的位置關系以及定值問題,考查了方程、轉化與化歸等數學思想以及坐標法的應用,檢驗了數學運算、邏輯推理等數學核心素養.試題平中見奇,內涵豐富,符合新課標理念.

2.試題解答

3.試題背景

為了揭示題1 的背景,下面先給出高等幾何中的幾個定義和性質.

(1)調和點列與調和線束

定義1一條直線上的四個點A,B,C,D如果滿足,那么稱A,B,C,D為調和點列,亦稱B,D調和分割線段AC.過調和點列A,B,C,D所在直線外一點P,向A,B,C,D引四條線束,稱這四條線束PA,PB,PC,PD為調和線束.

性質1如圖1,設直線l與調和線束PA,PB,PC,PD分別交于點A′,B′,C′,D′,則A′,B′,C′,D′為調和點列.

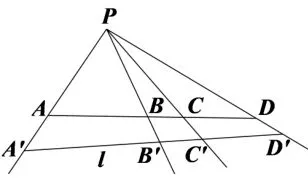
圖1

性質2如圖2,如果PA,PB,PC,PD為調和線束,且PD//AC,則PB平分線段AC.

圖2

(2)極點與極線

定義2如圖3,若點P不在圓錐曲線Γ 上,過點P引兩條割線與Γ 依次交于E,F,G,H四點,直線EH與FG交于點M,直線EG與FH交于點N,則直線MN為點P關于Γ 的極線,直線PM為點N關于Γ 的極線,直線PN為點M關于Γ 的極線.若點P在圓錐曲線Γ 上,則過點P的切線即為極線.

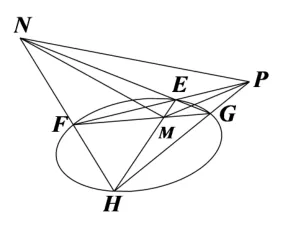
圖3

定義3已知有心圓錐曲線Γ:ax2+by2=1 (ab/=0),極點P(x0,y0),則點P關于圓錐曲線Γ 的極線方程為ax0x+by0y=1,當y0=0 時,極線方程為ax0x=1.

若圓錐曲線Γ 是拋物線y2=2px(p ＞0),極點P(x0,y0),則點P關于圓錐曲線Γ 的極線方程為y0y=p(x+x0),當y0=0 時,極線方程為x0+x=0.

性質3如圖4,已知點P是圓錐曲線Γ 外一點,點P關于Γ 的極線AB與Γ 相交于A,B兩點,則PA、PB是Γ 的兩條切線;過點P的一條割線交Γ 及極線AB于點M,N,Q,則P,M,Q,N為調和點列.

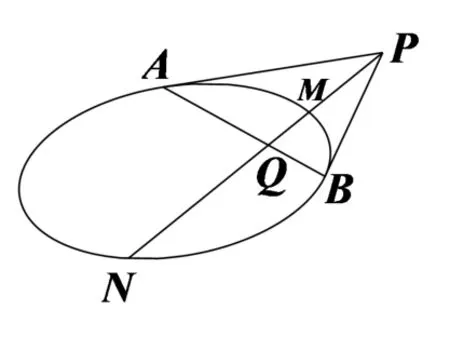
圖4

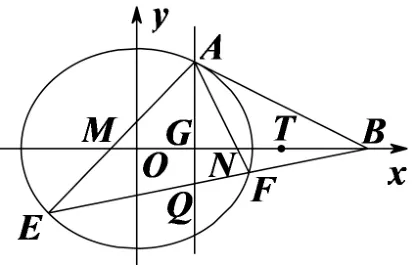
圖5

本題經過推廣,還可以得到更一般的結論.

定理如圖6,已知橢圓C:=1 (a ＞b ＞0),點B是橢圓C外一點,過點B作橢圓C的兩條切線PA、PD,其中A、D是切點,直線OB與直線AD交于點G,T為BG的中點,過點B的直線與橢圓C交于E,F兩點,直線AE,AF與直線OB分別交于M,N兩點,則|TM|·|TN|為定值|TG|2.

圖6

圖7

4.性質應用

簡解(1)橢圓C的方程為=1.

(2)如圖8,連接AB,設l與直線x=-2 交于點D,因為B(-4,0),所以點B關于橢圓C的極線方程是x=-2,于是點B,M,D,N是調和點列,即AB,AM,AD,AN是調和線束.因為PQ//AD,所以AB平分線段PQ,故

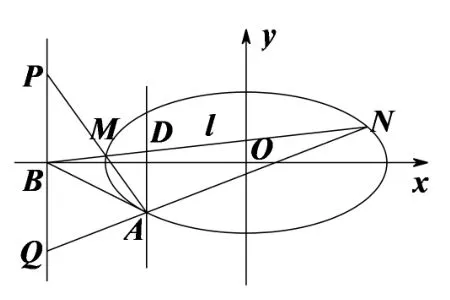
圖8

題目4(2018 年高考北京卷理科第19 題)已知拋物線C:y2=2px經過點P(1,2),過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N.

(1) 求直線l的斜率的取值范圍;(2) 設O為原點,為定值.

簡解(1) 略,直線l的斜率的取值范圍是(-∞,-3)∪(-3,0)∪(0,1).

(2) 如圖9,連接PQ,OP,設l與OP交于點D,不妨設M在線段OQ上,N在線段OQ的延長線上,即λ ＞0,μ ＜0.由已知可得直線PQ的方程為y=x+1,與拋物線C的方程y2=4x聯立,得x2-2x+1=0,此時Δ=0,所以直線PQ是拋物線C的切線,P是切點.又y軸也是拋物線C的切線,O是切點,所以點Q關于拋物線C的極線是OP,所以Q,A,D,B是調和點列,于是PQ,PA,PD,PB是調和線束,由此得Q,M,O,N是調和點列,所以,即,整理得=2,即為定值.

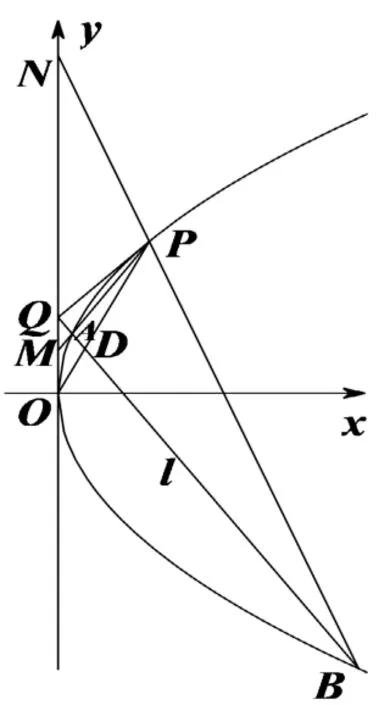
圖9