考慮備切機組涉頻特性的高頻切機優化方法

姜惠蘭，李希鈺，肖 瑞

（天津大學智能電網教育部重點實驗室，天津 300072）

隨著我國能源轉型的不斷推進，風力、光伏等新能源的并網規模也在逐年擴大，使得電網結構相對薄弱的區域型送端電網中出現直流外送通道故障產生大量的過剩功率，容易引發嚴重的高頻問題，威脅電網的安全穩定運行。作為頻率緊急控制措施，高頻切機方案是抵御過剩功率故障下高頻危害的重要控制措施[1-2]。隨著新能源場站級涉頻技術的不斷成熟，高頻切機方案中備切機組的涉頻特性差異也越來越明顯，所以考慮機組涉頻特性的高頻切機方案優化方法有待進一步研究。

文獻[3-4]分析了不同類型機組的頻率響應特性，為保證高頻切機方案對不同程度負荷缺失的適應性，采用基于“最小欠切原則”的方法分輪次確定高頻切機方案；文獻[5-7]根據工程運行經驗給出多個備選切機方案，通過對比各方案的實施效果確定最優方案；文獻[8]針對系統頻率響應特性及影響因素進行分析，考慮高頻切機方案與機組超速保護、低頻減載保護等控制措施的協調配合，確定高頻切機方案各輪次的動作頻率、動作延時、切機量及切機類型；文獻[9]將高頻切機方案整定模型分解為首輪單次切機總量子模型和分輪次切機量優化子模型，依據系統暫態頻率裕度指標和機組與故障點間的電氣距離進行機組組合方式的優化；文獻[10]依據系統送端線路故障情況構造罰函數，按故障程度及概率確定適應各故障情況的高頻切機方案。

現有高頻切機組合方案的尋優方法，一方面忽略了系統頻率特性曲線在不同時間區段的影響因素、特征的差異以及相互關聯性，不夠全面體現高頻切機方案實施效果的優勢；另一方面，高頻切機方案在整定滿足系統頻率約束的各輪次切機量時，忽略了被切除機組的涉頻特性差異對切機方案的影響，難以達到最優的實施效果和對所有故障情況的適用性。本文通過分析高頻切除機組對系統頻率響應特性的影響，給出了一種依據不同頻率響應階段下系統頻率特性差異評價高頻切機方案實施效果的目標函數，在此基礎上，提出考慮機組涉頻特性的高頻切機方案遞進修正優化方法。它是在滿足系統頻率響應變化曲線約束的前提下，依據頻率變化曲線在不同頻率響應階段下的特性差異和影響因素，建立切機量最小和評價指標最優的多目標優化模型，同時制定了切機方案各輪次初始切機量和遞進修正整定量的措施，達到權衡總切機量最小與實施效果最優的效果。

1 備切機組涉頻特性對系統高頻響應的影響

本文采用電力系統等值模型分析系統高頻響應過程。圖1所示的分析高頻響應的等值模型，考慮了負荷頻率調節效應，機組的功率調節和調速器慣性響應。

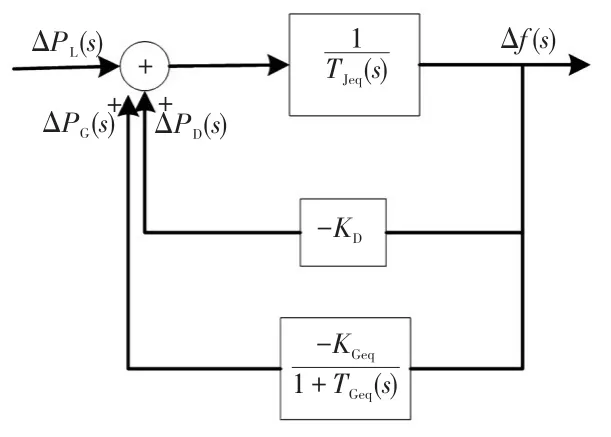
圖1 高頻響應等值模型Fig.1 Equivalent model of over-frequency response

圖1中：ΔPL為過剩功率，Δf為系統頻率變化量，ΔPG為同步機組出力改變量，ΔPD為負荷變化量，TJeq為系統等值慣性時間常數，KGeq為系統等值單位調節功率，TGeq為等值機組調速器時間常數，KD為負荷頻率調節效應系數，s為拉普拉斯算子。

由圖1可以得到系統頻率響應過剩功率變化的傳遞函數G(s)[11]為

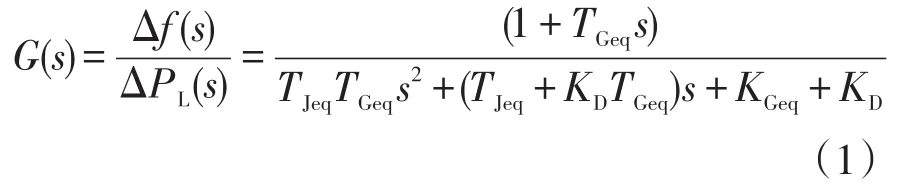
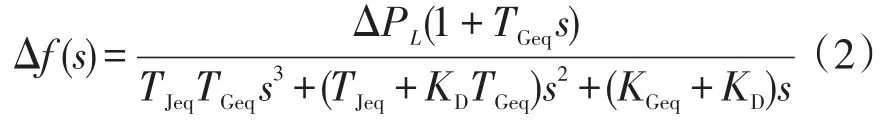
通過拉氏反變換得到頻率偏差的時域表達式為

可見，頻率暫態變化特性主要受系統的等值慣性時間常數、調節功率能力影響，而機組涉頻特性差異也正體現在自身的慣性時間常數和單位調節功率上。

設切機動作后的系統等值慣性時間常數為TJeq.trip，等值單位調節功率為KGeq.trip，上述參數均以系統總額定容量為基準值，則有

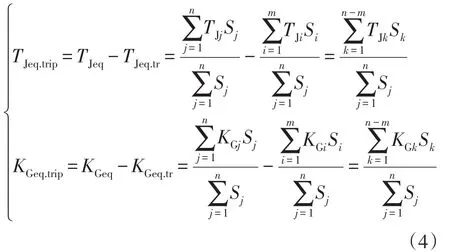
式中：n為機組總臺數；m為切除的備切機組臺數；TJeq.tr和KGeq.tr分別為被切除機組的等值慣性時間常數和等值單位調節功率；TJi、KGi和Si分別為機組i的慣性時間常數、單位調節功率和額定容量。

由式（4）可以看出，隨著高頻切機逐輪次動作切除發電機組，TJeq.tr和KGeq.tr會不斷增大，使得切機動作后的系統等值慣性時間常數TJeq.trip和KGeq.trip隨動作輪次的增加不斷減小，且系統等值涉頻參數水平會因被切除機組的涉頻特性差異而不同，進而影響系統在過剩功率故障下的高頻響應過程，這也是不同高頻切機機組組合方式會產生不同的實施效果的原因。

2 評價不同頻率響應階段下高頻切機實施效果的目標函數

2.1 頻率響應階段的劃分

系統等效轉子運動方程為

式中：TJeq為系統等效慣性時間常數；PmΣ為總機械功率；PeΣ為總電磁功率；Δf為系統頻率偏差。

從式（5）可知：dΔf/ dt的方向能夠反映系統總機械功率PmΣ和總電磁功率PeΣ的關系。若PmΣ＞PeΣ，則dΔfdt＞0 ；若PmΣ＜PeΣ，則dΔf/ dt＜0。本文主要依據dΔf/ dt的變化方向來劃分系統高頻響應時間階段，如圖2所示。階段I：從故障時刻t0到頻率最高tmax區段，dΔf/ dt＞0，且由最大值逐漸衰減至0；階段II：從頻率最高tmax到頻率最低tmin區段，dΔf/ dt＜0 ；階段III：從頻率最低tmin到穩態值t∞的區段，系統經小幅波動達到穩態。該時段劃分方法可以利用同一階段下的頻率響應變化基本具有一致性的特點，合理地分析不同階段下的高頻切機方案實施效果需求的差異。

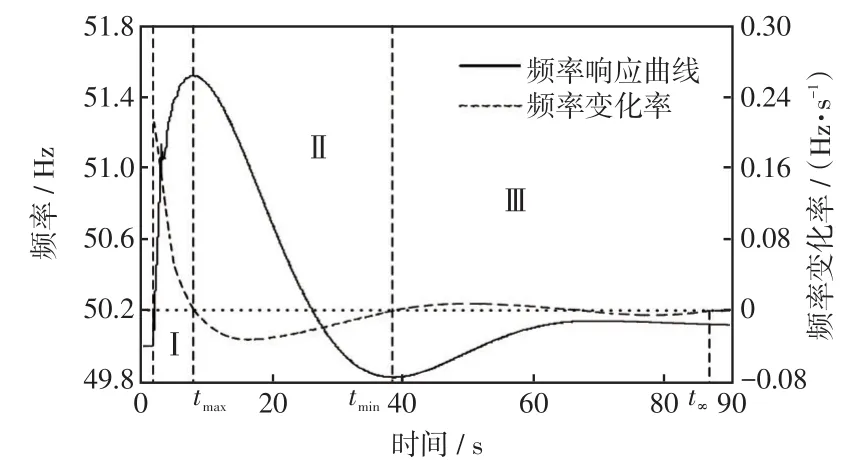
圖2 系統頻率響應階段劃分示意Fig.2 Schematic of division of system frequency response stages

2.2 評價高頻切機方案實施效果的目標函數

對所劃分的3個頻率響應階段，依據頻率變化特點和影響因素的不同，構建了相應階段的目標函數。

1）階段I的目標函數

在階段I，系統頻率時域響應為一條單調上升曲線，最大值和變化率越小，對應的高頻切機方案的實施效果越好。影響這些指標的主要因素包括該響應階段的系統慣量水平與功率調節能力，因此定義系統平抑功率ΔPm來綜合反映抵消故障功率過剩的能力，即

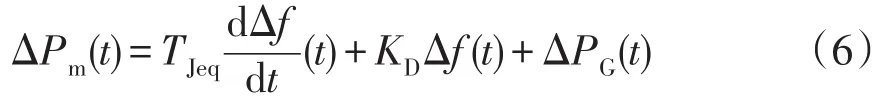
式中，ΔPG為機組一次調節隨頻率偏差的出力變化。

可以看出，系統平抑功率ΔPm在階段I隨系統頻率偏差Δf和頻率變化率dΔf/ dt的增大而不斷增大；系統等值機組的涉頻特性越好，即TJeq和KGeq越大，系統平抑功率水平越高，頻率偏差及其變化率將越小。

考慮到高頻切機動作通常是在階段I完成，各輪次動作后系統等值機組的涉頻參數會發生變化，也即系統的涉頻特性參數僅在相鄰動作輪次間保持不變，切機機組組合方式的不同使得相鄰輪次間平抑功率增量存在差異。為了更合理地運用系統平抑功率來評價高頻切機方案在階段I下的實施效果，應分別計算各輪次動作之間的平抑功率增量并進行累加。因此，所構建的響應階段I下的目標函數為

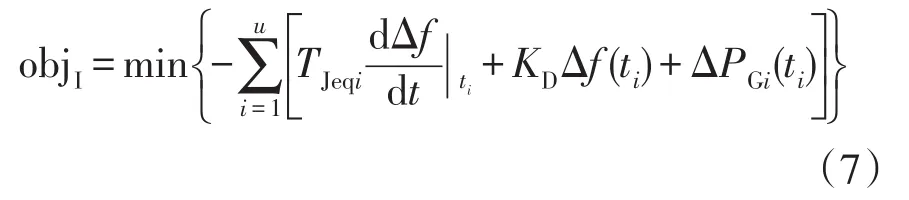
式中：u為切機方案的動作輪次；TJeqi為第i輪動作后系統的等效慣性時間常數；ΔPGi為第i輪動作后機組調速器出力改變量；ti為第i輪動作時刻。

2）階段Ⅱ的目標函數

在階段Ⅱ下，系統頻率時域響應為一條單調下降的曲線。系統頻率從最大偏差到最小偏差的最大跌落深度越小、所用的跌落時間越短，對應的高頻切機方案的實施效果越好。本文采用綜合考慮系統頻率最大跌落深度和所用跌落時間同時最小來評價該階段的實施效果。所構建的響應階段Ⅱ下的目標函數為

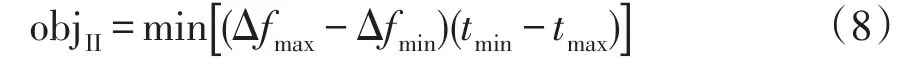
式中：Δfmax和Δfmin分別對應系統頻率偏差的最大值和最小值；tmax和tmin分別對應系統頻率達到最大偏差和最小偏差的時間。

3）階段Ⅲ的目標函數

在階段Ⅲ下，系統頻率將從最小偏差逐漸恢復至穩態頻率。頻率恢復至穩態值所用的時間越短，且恢復過程中圍繞穩態頻率的波動越小，對應高頻切機方案的實施效果越好。為了兼顧階段Ⅲ下縮短系統頻率恢復時間及抑制頻率波動的需求，可以用頻率偏差時域積分絕對值的大小來評價該時段高頻切機方案實施效果。所構建的響應階段Ⅲ下的目標函數為

式中，t∞為頻率達到穩態值的時間。

3 高頻切機方案整定優化的數學模型

探求保障系統頻率穩定的緊急控制措施的高頻切機優化方案時，在滿足頻率穩定指標要求的前提下考慮高頻切機方案的經濟性及實施效果，同時還需要考慮與機組超速保護和低頻減載等頻率緊急控制措施的配合[12]。因此，針對高頻切機機組組合優化問題，本文建立了相適應的數學模型。

1）目標函數

目標函數1：高頻切機方案的總切機量最小，有

目標函數2：高頻切機方案的實施效果最優，有

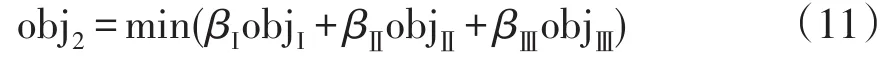
式中，βI、βⅡ和βⅢ分別表示頻率響應階段Ⅰ、Ⅱ、Ⅲ各子目標所占的權重，可通過線性加權評估法[12]確定。

2）約束條件

根據電力行業的系統暫態及穩態頻率標準，以及機組超速保護等緊急控制措施的動作頻率[13]，所建立的約束條件為

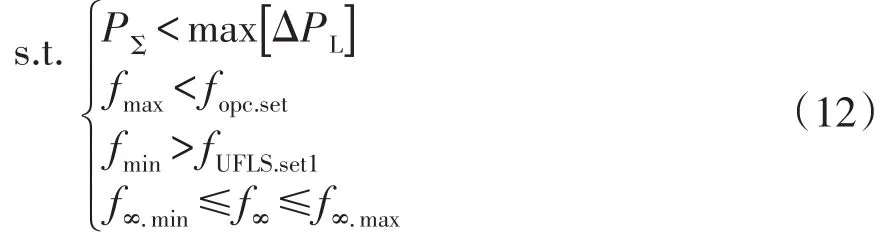
其中，約束條件1表示總切機量PΣ不得超過可能的最大過剩功率；約束條件2表示系統暫態頻率最大值fmax不應高于機組超速保護動作值fopc.set；約束條件3表示暫態頻率最小值fmin不應低于低頻減載的第1級動作值fUFLS.set1；約束條件4表示系統穩態頻率f∞應在允許的穩態頻率上限值f∞.max和下限值f∞.min之間。

4 考慮機組涉頻特性的高頻切機方案優化

目前高頻切機整定優化方法中，有的研究依據最嚴重故障情況確定的總切機量人為整定各輪次切機量，難以保證所有故障情況滿足頻率約束條件；有的研究沒有考慮備切機組涉頻特性差異對頻率響應特性的影響，給出的切機方案不是最優的；還有的研究對整個暫態期間構建相同的優化目標函數，忽略了頻率特性曲線在不同階段下的影響因素和特征的差異，不能全面體現高頻切機方案實施效果的優勢。本文提出一種計及備切機組涉頻特性差異的高頻切機方案遞進修正優化方法，高頻切機方案的確定過程包括基于備切機組等容量模型替換的初始切機量整定和基于NSGA-Ⅱ算法遞進修正切機量的高頻切機機組組合優化。

4.1 基于備切機組等容量模型替換的初始切機量整定

考慮到備切機組涉頻特性差異對系統頻率響應的影響，為了有效解決備切機組涉頻特性差異及切除順序不同對切機量整定的影響問題，本文采用將備切機組等容量模型替換的方式，即將系統等效模型中的備切機組等容量替換為常規新能源機組（出力穩定且不響應系統頻率的變化），形成等容量替換模型。由于等容量替換模型降低了等值慣量水平和頻率調節能力，基于該模型整定的初始切機量是保守的，使得實際模型在不同故障情況下系統頻率特性能夠滿足約束的同時還留有一定的裕度。初始切機量的整定步驟如下：

步驟1設定切機方案動作輪次u次、各輪次動作頻率fi和動作延時td.i,i=1～u；

步驟2將系統中可能出現的故障情況按過剩功率由小到大排序，形成故障集，并將備切機組按額定容量由小到大進行排列，形成備切機組集合；

步驟3按照故障集順序進行仿真計算，記錄系統頻率響應曲線最大值fmax剛好不超過第（i+1）輪次動作頻率的故障序號為Fi，對應的過剩功率為第i輪切機動作所適應的最大過剩功率ΔPmax.i,i=1～u；

步驟4調整切機量，使第i輪動作后，所有故障序號不超過Fi的故障情況下的頻率特性曲線都滿足頻率穩定約束。記錄第i輪次切機量為ΔPtrip.i,i=1～u。

4.2 基于NSGA-Ⅱ算法遞進修正切機量的高頻切機機組組合優化

在高頻切機機組組合優化數學模型的基礎上，采用NSGA-Ⅱ算法對高頻切機機組組合多目標優化問題進行求解。本文以總切機量最小和高頻切機實施效果最優為目標進行優化，由最優折衷解得到的高頻切機方案實現了對兩個目標的兼顧。總體優化流程如圖3所示。

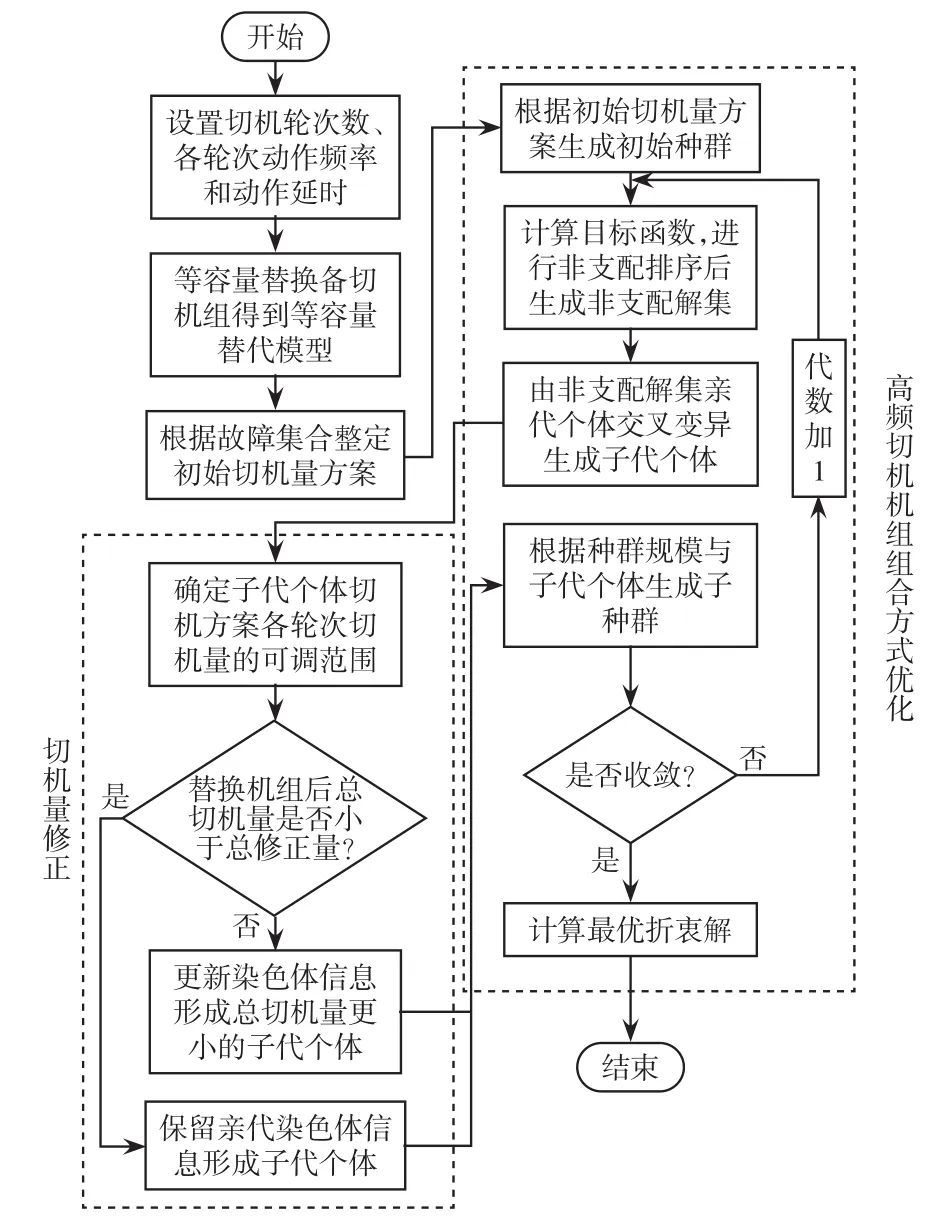
圖3 高頻切機方案整定優化流程Fig.3 Optimization process of setting of over-frequency generator tripping scheme

高頻切機方案整定的目的是優化出各輪次動作機組的組合，所以本文給出的遺傳染色體是待切機組的動作順序組合，而且采用十進制整數編碼來反映備切機組的動作輪次，編碼方式為

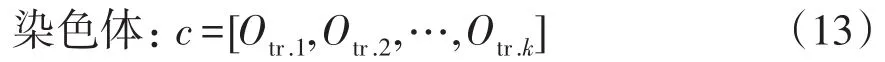
式中：k為備切機組臺數；Otr.1～Otr.k分別為對應備切機組的動作順序編碼，表示為

當Otr.i=0時，表示編號為i的備切機組不參與切機方案；當Otr.i=j時，表示編號為i的待切機組參與切機方案的第j輪動作。

尋找高頻切機方案的優化過程是通過對實際模型仿真計算而逐代演化的，在NSGA-Ⅱ迭代過程中，通過交叉變異操作隨機生成的子代個體切機方案總切機量將發生變化，可能不同于初始切機量。由前面分析可知，用等容量替換得到的初始切機量應用于實際系統時是有一定裕量的，為了高頻切機方案的經濟性目標，交叉變異操作應滿足以下原則：

（1）交叉操作生成的子代個體總切機量應等于親代，二者僅機組組合方式不同；

（2）變異操作生成的子代個體總切機量應小于親代。

基于上述原則通過交叉變異操作可以實現子代個體切機方案總切機量的逐代修正，步驟如下：

步驟1根據等容量替換模型與實際模型的涉頻特性差異，確定初始切機量方案的總切機修正量；

步驟2根據各輪次初始切機量與在實際模型中適應的最大過剩功率的差值，將總切機修正量分配到各動作輪次，確定各輪次的切機修正量最大范圍；

步驟3執行變異操作時，在各輪次的切機修正量范圍內，用小容量機組替換親代個體中的備切機組進行個體切機量修正，若滿足頻率約束則該個體將作為子代個體。

5 仿真分析

圖4為含新能源的區域電網接線圖，系統可能出現的故障情況及相應過剩功率如表1所示。本文對高頻切機方案遞進修正優化方法進行了仿真，并與文獻[3]的整定方法進行了對比分析，以驗證所提方法的優勢。

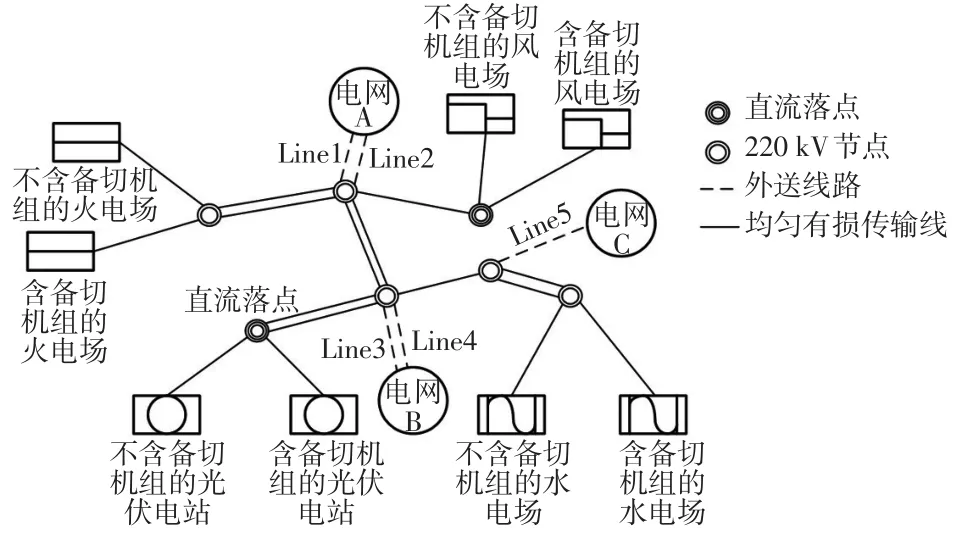
圖4 區域電網接線圖Fig.4 Wiring diagram of regional grid

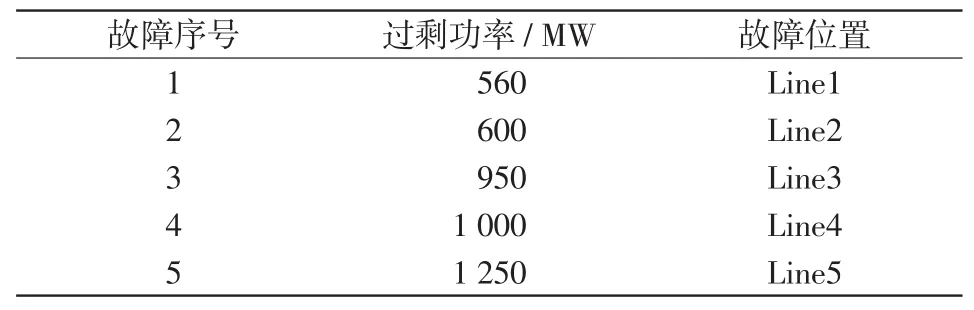
表1 區域電網故障Tab.1 Faults in regional grid

5.1 初始切機量的整定計算

按照工程經驗給定切機方案動作輪次、各輪次動作頻率及動作延時，并用備切機組等容量模型替換的方式，整定出的各輪次初始切機量和相應的最大過剩功率，如表2所示。

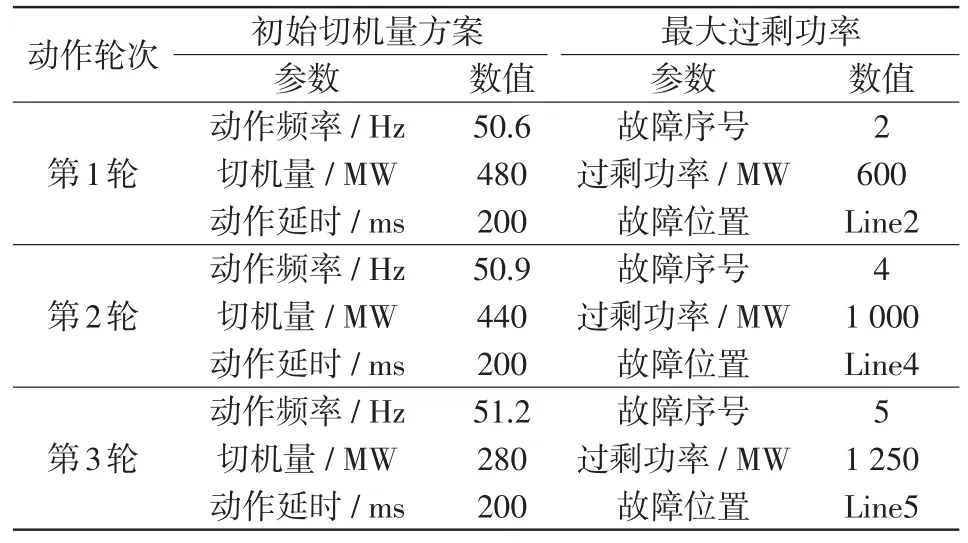
表2 初始切機量方案及相應的最大過剩功率Tab.2 Initial generator tripping scheme and the corresponding maximum excess power

5.2 高頻切機機組組合優化結果

依據所確定的初始切機量生成NSGA-Ⅱ算法的初始種群，種群規模設置為24，頻率響應曲線各時間區段評價指標的線性加權值βⅠ、βⅡ和βⅢ分別為0.3、0.3和0.4。通過基于NSGA-Ⅱ算法對高頻切機機組組合方案進行遞進修正優化，得到的Pareto最優解集如圖5所示，由其最優折衷解可得高頻切機機組組合方案。

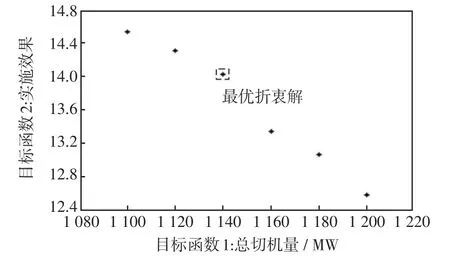
圖5 二維空間Pareto最優解集前沿Fig.5 Frontier of Pareto optimal solution set in twodimensional space

實際上，在尋優的迭代過程中，每一代產生的非支配解集都有對應的最優折衷解，也分別對應兩個目標函數。最優折衷解目標函數隨迭代次數的變化如圖6所示。圖6（a）目標函數1所代表的高頻切機方案總切機量隨迭代次數的變化情況，圖6（b）目標函數2所代表的高頻切機方案實施效果隨迭代次數的變化情況。從圖6（a）可以看出，總切機量經過7代修正，由初始切機量1 200 MW逐漸減小至1140MW，證明了基于NSGA-Ⅱ優化算法遞進修正切機量方法的有效性。從圖6（b）可以看出，評價高頻切機方案實施效果的目標函數2的計算值總體呈逐代減小，同樣證明了本文所提優化方法的有效性。

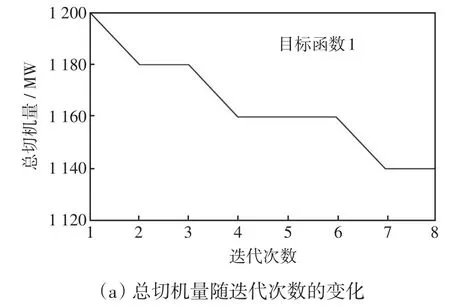
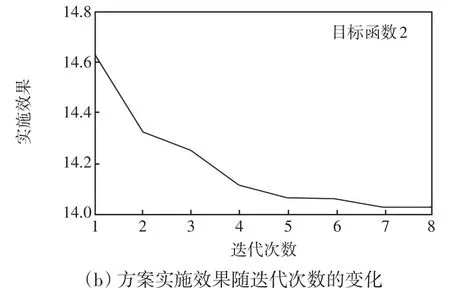
圖6 最優折衷解目標函數隨迭代次數的變化Fig.6 Changes in objective functions of optimal compromise solution with the number of iterations

5.3 高頻切機方案對比分析

本文還與文獻[6]所述整定方法進行了仿真對比，得到的兩種高頻切機方案示于表3中，過剩功率最嚴重故障情況下的系統頻率特性曲線如圖7所示。由表3可知，在切機方案的動作輪次、動作頻率及動作延時相同的前提下，采用本文方法得到的高頻切機機組組合方案，其總切機量為1 140 MW，相較于文獻[6]的總切機量1 180 MW，減少了40 MW，提高了高頻切機方案的經濟性；另一方面，由圖7可見，本文方法的高頻切機方案作用下的頻率響應曲線，暫態頻率的最高值為51.23 Hz，頻率的跌落深度為1.47 Hz，恢復至穩態頻率的時間為88 s，對應計算的目標函數2為obj2=14.027；而文獻[6]方法的高頻切機方案作用下的頻率響應曲線，暫態頻率的最高值為51.48 Hz，頻率的跌落深度為1.70 Hz，恢復至穩態頻率的時間為90 s，對應計算的目標函數2為obj2=15.050，說明用本文方法優化出的高頻切機方案實施效果更優。

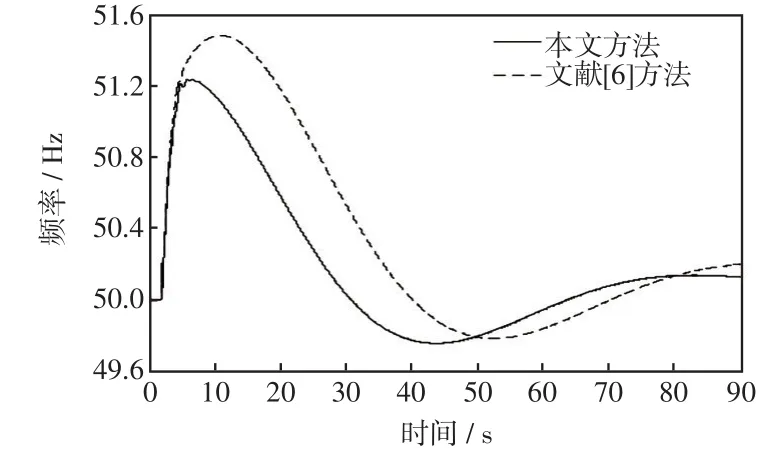
圖7 高頻切機方案的實施效果對比Fig.7 Comparison of implementation effect between different over-frequency generator tripping schemes

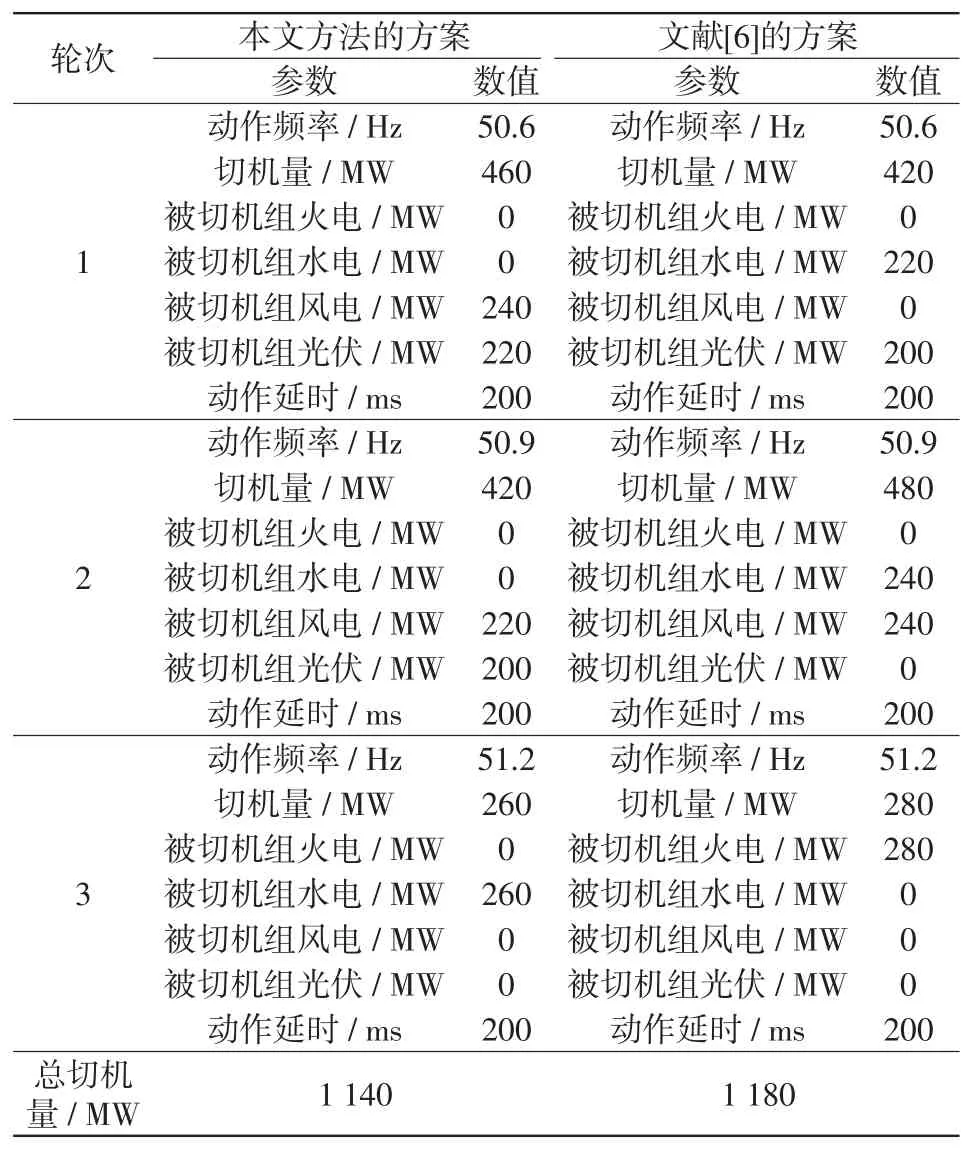
表3 高頻切機方案的對比Tab.3 Comparison between different over-frequency generator tripping schemes

6 結論

（1）采用備切機組等容量模型替換的方法整定初始切機量，可以避免備切機組涉頻特性差異及切除順序不同對切機量整定的影響。

（2）構建了評價頻率響應不同階段下高頻切機實施效果的目標函數，體現了備切機組涉頻特性差異與系統高頻響應特性的關聯性.。

（3）基于NSGA-Ⅱ的高頻切機機組組合遞進修正優化方法，兼顧了高頻切機方案的經濟性和實施效果，在實際應用中具有更強的優勢。