美英早期代數(shù)教科書(shū)的代數(shù)價(jià)值觀探析

邵愛(ài)娣，劉思璐，汪曉勤

美英早期代數(shù)教科書(shū)的代數(shù)價(jià)值觀探析

邵愛(ài)娣1，劉思璐2，汪曉勤2

（1．上海市延安初級(jí)中學(xué)，上海 200050；2．華東師范大學(xué) 教師教育學(xué)院，上海 200062）

選取1800—1959年間出版的155種美英早期代數(shù)教科書(shū)，考查其前言及正文引言部分有關(guān)代數(shù)教育價(jià)值觀的內(nèi)容．研究發(fā)現(xiàn)代數(shù)教育價(jià)值觀可分為學(xué)科基礎(chǔ)、思維訓(xùn)練、品質(zhì)培養(yǎng)、實(shí)際應(yīng)用、數(shù)學(xué)交流、情感信念、學(xué)科優(yōu)勢(shì)7類．以20年為一個(gè)時(shí)間段，每個(gè)時(shí)間段7類價(jià)值觀都不同程度地出現(xiàn)．從代數(shù)運(yùn)算、公式、方程、圖象和問(wèn)題5個(gè)方面分析了代數(shù)教育價(jià)值觀在教科書(shū)中的體現(xiàn)．啟示今天的中學(xué)代數(shù)教學(xué)與教科書(shū)編寫(xiě)要注重代數(shù)價(jià)值觀的實(shí)現(xiàn)．

代數(shù)；教育價(jià)值；語(yǔ)言；思維；應(yīng)用

1 問(wèn)題提出

理想的教學(xué)要求教師不僅要知道“教什么”“如何教”，還要知道“為何教”[1]，教師只有深刻理解數(shù)學(xué)的價(jià)值，才能知道“為何教”．關(guān)于數(shù)學(xué)的價(jià)值，《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》（以下簡(jiǎn)稱《標(biāo)準(zhǔn)》）指出：“數(shù)學(xué)是自然科學(xué)的重要基礎(chǔ)，在形成人的理性思維、科學(xué)精神和智力發(fā)展中發(fā)揮著不可替代的作用，它還是表達(dá)與交流的語(yǔ)言，其應(yīng)用滲透在人們?nèi)粘Ｉ畹母鱾€(gè)方面．”《標(biāo)準(zhǔn)》還在課程目標(biāo)中提出“讓學(xué)生認(rèn)識(shí)數(shù)學(xué)的科學(xué)價(jià)值、應(yīng)用價(jià)值、文化價(jià)值、審美價(jià)值”的要求[2]．調(diào)查研究表明[3-4]，學(xué)生在初等教育時(shí)期，受以功利性和實(shí)用性為主的升學(xué)考試的影響，隨著年段的升高，其數(shù)學(xué)觀各維度的水平逐步下降，高中最低．鑒于此，一些學(xué)者大力提倡在數(shù)學(xué)教學(xué)中凸顯數(shù)學(xué)的價(jià)值，改變學(xué)生消極的數(shù)學(xué)觀[5-7]．

代數(shù)是數(shù)學(xué)的一個(gè)分支，在中小學(xué)數(shù)學(xué)教育中占有重要地位．要在代數(shù)教學(xué)中體現(xiàn)數(shù)學(xué)的價(jià)值，首先需要深入探討代數(shù)學(xué)所特有的價(jià)值．雖然有許多學(xué)者在這方面[8-10]做過(guò)研究，但很少見(jiàn)到基于歷史視角的文獻(xiàn)研究．事實(shí)上，對(duì)于代數(shù)學(xué)價(jià)值的探討可以上溯至17世紀(jì)，法國(guó)數(shù)學(xué)家笛卡兒稱“一切問(wèn)題均可轉(zhuǎn)化為代數(shù)問(wèn)題，一切代數(shù)問(wèn)題均可轉(zhuǎn)化為方程問(wèn)題”．19世紀(jì)以來(lái)，部分西方代數(shù)教科書(shū)中或多或少都對(duì)代數(shù)學(xué)教育價(jià)值作過(guò)探討，對(duì)這些代數(shù)教科書(shū)的價(jià)值觀進(jìn)行考查，一方面能幫助今天的教師更深刻、全面地理解代數(shù)的教育價(jià)值，另一方面也能夠?yàn)榻袢沾鷶?shù)教學(xué)和教科書(shū)編寫(xiě)帶來(lái)一定的啟示．對(duì)1800—1959年間出版的美英早期代數(shù)教科書(shū)進(jìn)行考查，試圖回答以下問(wèn)題：早期代數(shù)教科書(shū)提出了代數(shù)學(xué)的哪些教育價(jià)值？這些價(jià)值在教科書(shū)中是如何體現(xiàn)的？對(duì)今日中學(xué)代數(shù)教學(xué)和教科書(shū)編寫(xiě)有何啟示？

2 研究方法

2.1 對(duì)象選取

研究者詳細(xì)閱讀Hathi Trust數(shù)字圖書(shū)館中兩百余種出版于1800—1959年間的美國(guó)和英國(guó)代數(shù)教科書(shū)的前言和正文引言部分，從中篩選出論及代數(shù)學(xué)價(jià)值的教科書(shū)作為研究對(duì)象．關(guān)于代數(shù)價(jià)值的表述有以下4類：（1）直接描述代數(shù)學(xué)的價(jià)值；（2）描述數(shù)學(xué)的價(jià)值，因其出現(xiàn)在代數(shù)教科書(shū)的前言部分，將其歸為代數(shù)的價(jià)值；（3）描述該教科書(shū)或教科書(shū)的某一部分（如例題）所要達(dá)成的教育價(jià)值，因其出現(xiàn)在代數(shù)教科書(shū)的前言部分，將其歸為代數(shù)學(xué)的價(jià)值；（4）描述代數(shù)學(xué)中某一個(gè)知識(shí)點(diǎn)的價(jià)值．

對(duì)于同一作者再版的教科書(shū)，若書(shū)名不一致或書(shū)名雖同但內(nèi)容不一致，則視為不同的教科書(shū)，否則視為同一種．最終確定155種，其中112種在前言中論及代數(shù)學(xué)的價(jià)值，25種在正文引言部分論及代數(shù)學(xué)的價(jià)值，18種在前言和正文引言部分同時(shí)論及代數(shù)學(xué)的價(jià)值．若以20年為一段，則155種代數(shù)教科書(shū)的分布情況如圖1所示．

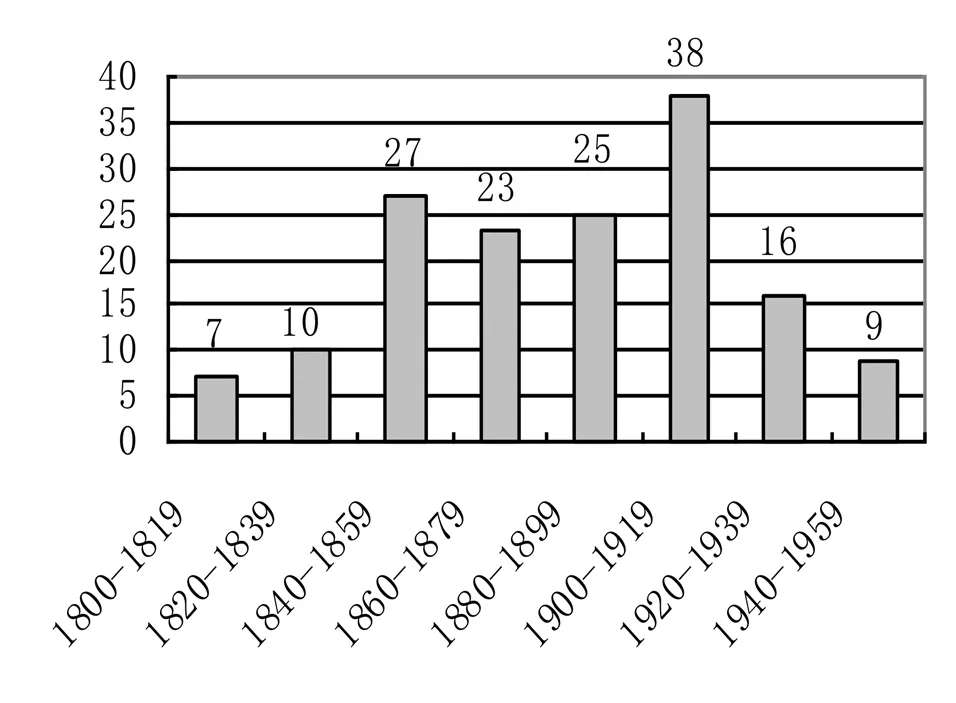
圖1 155種教科書(shū)的時(shí)間分布

2.2 分類框架的建立

早在1920年，Kelley在哥倫比亞大學(xué)《教師學(xué)院院刊》發(fā)表了一項(xiàng)關(guān)于中學(xué)代數(shù)價(jià)值的調(diào)查研究[11]．為了回答“中學(xué)代數(shù)的價(jià)值是什么”這個(gè)問(wèn)題，作者對(duì)數(shù)學(xué)家以及從事各行各業(yè)的人們進(jìn)行了一項(xiàng)調(diào)查．研究者對(duì)Kelley的調(diào)查結(jié)果進(jìn)行分析和歸類，據(jù)此形成初步的代數(shù)價(jià)值分類框架．運(yùn)用該框架對(duì)早期代數(shù)教科書(shū)的代數(shù)價(jià)值觀進(jìn)行統(tǒng)計(jì)時(shí)，根據(jù)統(tǒng)計(jì)情況，反過(guò)來(lái)又對(duì)分類框架進(jìn)行適當(dāng)修正，最終形成正式的代數(shù)價(jià)值分類框架，見(jiàn)表1．

表1 代數(shù)學(xué)價(jià)值的分類框架

2.3 分類統(tǒng)計(jì)

確定統(tǒng)計(jì)框架后，由兩位研究者運(yùn)用文本分析法對(duì)155種教科書(shū)的前言及正文引言部分進(jìn)行研究，提煉出其中關(guān)于代數(shù)價(jià)值觀的統(tǒng)計(jì)單位，根據(jù)分類框架對(duì)統(tǒng)計(jì)單位進(jìn)行分類．對(duì)于分類有爭(zhēng)議的地方，兩位研究者進(jìn)行再討論，直至全部一致．

統(tǒng)計(jì)結(jié)果顯示，共有81種教科書(shū)論及一類價(jià)值，47種教科書(shū)論及兩類價(jià)值，19種教科書(shū)論及三類價(jià)值，4種教科書(shū)論及四類價(jià)值，兩種教科書(shū)論及五類價(jià)值，兩種教科書(shū)論及六類價(jià)值．七類價(jià)值共出現(xiàn)270次，具體分布情況見(jiàn)圖2．

圖2 代數(shù)教育價(jià)值觀的分布

3 代數(shù)價(jià)值觀具體分類

3.1 學(xué)科基礎(chǔ)

共有61種教科書(shū)（占39.4%）提及代數(shù)作為學(xué)科基礎(chǔ)的價(jià)值，這也是代數(shù)價(jià)值觀中占比最多的一類．?dāng)?shù)學(xué)上，除了算術(shù)和初等幾何以外，沒(méi)有什么學(xué)科離得開(kāi)代數(shù)學(xué)．三角學(xué)、解析幾何、微積分，沒(méi)有代數(shù)學(xué)可謂寸步難行．作為跨學(xué)科基礎(chǔ)，代數(shù)知識(shí)是學(xué)習(xí)物理、化學(xué)、工程、商業(yè)等其它學(xué)科所需的必備知識(shí)．表2給出了代表性的具體觀點(diǎn)．

3.2 思維訓(xùn)練

共有59種教科書(shū)（占38.1%）提到代數(shù)的思維訓(xùn)練價(jià)值．通過(guò)學(xué)習(xí)代數(shù)，學(xué)生能夠提高智力，增強(qiáng)邏輯推理能力，發(fā)展抽象概括能力，并且能夠縝密地思考問(wèn)題等．總之，這里的思維訓(xùn)練是指跟腦力活動(dòng)相聯(lián)系的教育價(jià)值．表3給出了代表性的具體觀點(diǎn)．

3.3 品質(zhì)培養(yǎng)

共有13種教科書(shū)（占8.4%）提到代數(shù)在培養(yǎng)學(xué)生品質(zhì)方面的價(jià)值．這里的品質(zhì)指的是學(xué)生的行為和作風(fēng)顯示出來(lái)的品性、認(rèn)識(shí)等．無(wú)論是鍛煉堅(jiān)韌的意志、培養(yǎng)良好的習(xí)慣，還是培育探索精神、增加卓識(shí)遠(yuǎn)見(jiàn)，學(xué)習(xí)代數(shù)都帶來(lái)了很大的幫助．表4給出了代表性的具體觀點(diǎn)．

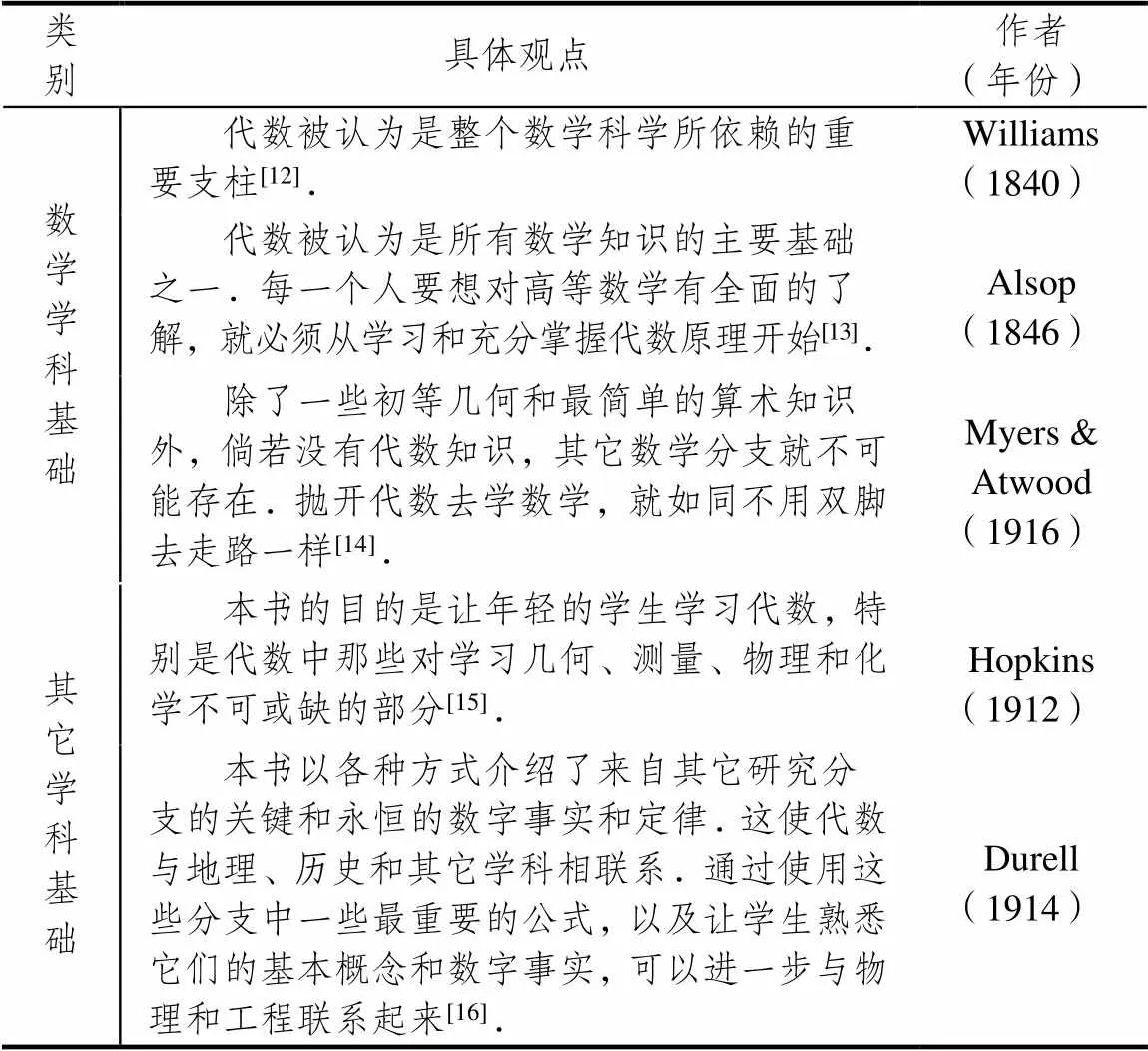
表2 關(guān)于學(xué)科基礎(chǔ)的代表性觀點(diǎn)

表3 關(guān)于思維訓(xùn)練的代表性觀點(diǎn)

表4 關(guān)于品質(zhì)培養(yǎng)的代表性觀點(diǎn)

3.4 實(shí)際應(yīng)用

共有43種教科書(shū)（占27.7%）提到了代數(shù)的實(shí)用價(jià)值．代數(shù)滲透于日常生活的許多方面，是從事多種行業(yè)的人員必需掌握的一門(mén)學(xué)科．表5給出了代表性的具體觀點(diǎn)．

3.5 數(shù)學(xué)交流

共有30種教科書(shū)（占19.4%）給出了代數(shù)在數(shù)學(xué)交流上的價(jià)值．代數(shù)語(yǔ)言是人們精確表達(dá)思想的強(qiáng)有力的工具，同時(shí)，代數(shù)也能鍛煉學(xué)生的表達(dá)能力．表6給出了代表性的具體觀點(diǎn)．

表5 關(guān)于實(shí)際應(yīng)用的代表性觀點(diǎn)

表6 關(guān)于數(shù)學(xué)交流的代表性觀點(diǎn)

表7 關(guān)于情感信念的代表性觀點(diǎn)

3.6 情感信念

共有13種教科書(shū)（占8.4%）認(rèn)為，學(xué)習(xí)代數(shù)有助于促進(jìn)學(xué)生對(duì)該學(xué)科的情感和信念的一種變化．這里的情感信念指的是學(xué)生對(duì)于數(shù)學(xué)學(xué)科或數(shù)學(xué)學(xué)習(xí)的一種態(tài)度的感受和認(rèn)識(shí)．表7給出了代表性的具體觀點(diǎn)．

3.7 學(xué)科優(yōu)勢(shì)

共有51種教科書(shū)（占32.9%）指出，與算術(shù)相比，代數(shù)有其獨(dú)特的優(yōu)勢(shì)．代數(shù)是算術(shù)的一種延續(xù)，它能解決用算術(shù)和幾何方法難以解決或不可能解決的問(wèn)題．表8給出了代表性的具體觀點(diǎn)．

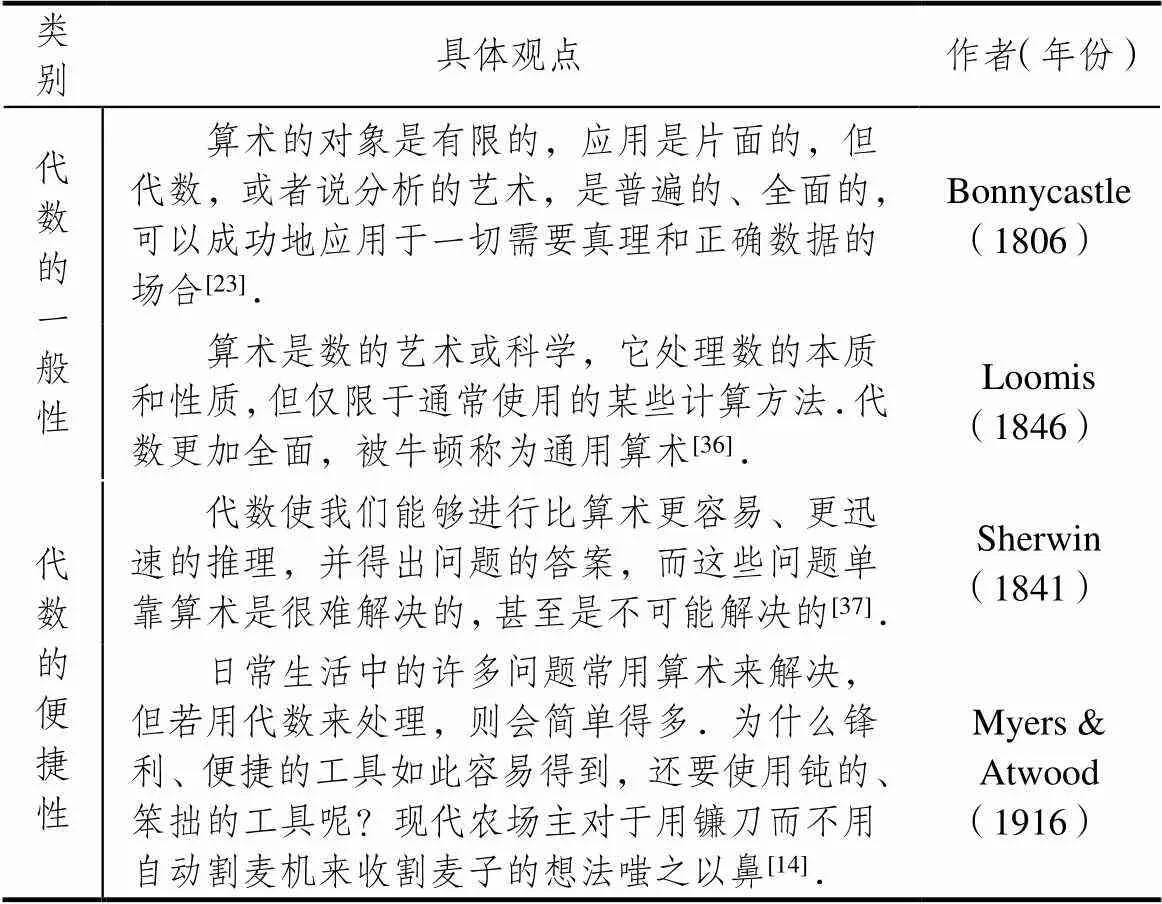
表8 關(guān)于學(xué)科優(yōu)勢(shì)的代表性觀點(diǎn)

4 代數(shù)價(jià)值觀的分布

由于每個(gè)年段的書(shū)本數(shù)量有差別，因而對(duì)上述7類代數(shù)價(jià)值觀在其年段所占比率進(jìn)行統(tǒng)計(jì)，并繪制圖表．圖3給出了各類價(jià)值分布的變化情況．

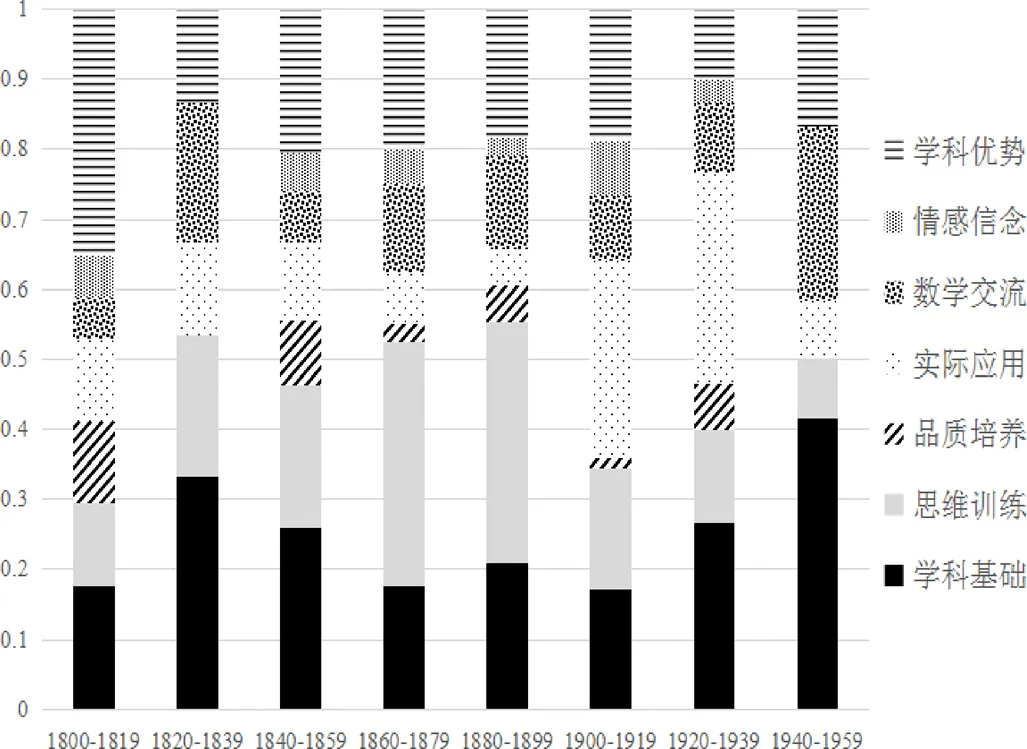
圖3 各類價(jià)值分布的變化情況

從圖3可見(jiàn)，以20年為一個(gè)時(shí)間段，則160年分成了8個(gè)時(shí)間段．其中品質(zhì)培養(yǎng)和情感信念出現(xiàn)在其中的6個(gè)時(shí)間段，其余5種價(jià)值出現(xiàn)在所有時(shí)間段．由此，19世紀(jì)到20世紀(jì)上半葉，代數(shù)教科書(shū)的編寫(xiě)者對(duì)代數(shù)的7種教育價(jià)值都有所關(guān)注．總的來(lái)說(shuō)，早期代數(shù)教科書(shū)呈現(xiàn)出了代數(shù)教育價(jià)值的多樣性．就單個(gè)價(jià)值而言，學(xué)科基礎(chǔ)和思維訓(xùn)練兩種價(jià)值占比最高．而變化比較明顯的是思維訓(xùn)練和實(shí)際應(yīng)用，19世紀(jì)末，思維訓(xùn)練占比較高，進(jìn)入20世紀(jì)之后，實(shí)際應(yīng)用占比迅速上升，這與20世紀(jì)初西方的數(shù)學(xué)教育改革運(yùn)動(dòng)息息相關(guān)．

5 代數(shù)價(jià)值觀在教科書(shū)中的體現(xiàn)

在對(duì)早期代數(shù)教與學(xué)的研究中發(fā)現(xiàn)，Hotz從加法和減法、乘法和除法、方程和公式、問(wèn)題、圖象5個(gè)方面制定了代數(shù)測(cè)試量表[38]；Durell從口頭和書(shū)面問(wèn)題、圖象、公式、新穎的例子等方面給出了代數(shù)教學(xué)的建議[39]；而Thorndike從公式、方程、問(wèn)題、圖象4個(gè)方面闡述了學(xué)習(xí)代數(shù)需要具備的能力[40]．因此，早期教科書(shū)編寫(xiě)者比較注重學(xué)生對(duì)于代數(shù)運(yùn)算、公式、方程、圖象和問(wèn)題5個(gè)方面的學(xué)習(xí)．研究者將從這5個(gè)方面來(lái)分析代數(shù)價(jià)值觀在教科書(shū)中的體現(xiàn)．

5.1 代數(shù)運(yùn)算

相比于算術(shù)，代數(shù)運(yùn)算代表了更一般化的數(shù)字運(yùn)算，因而早期代數(shù)教科書(shū)通過(guò)代數(shù)運(yùn)算來(lái)培養(yǎng)學(xué)生的抽象和概括能力．如Lyman等在講解多項(xiàng)式乘以多項(xiàng)式時(shí)類比兩位數(shù)豎式乘法的方式[41]，如圖4，要把32乘以24，可以先把30+2乘以4，然后再乘以20，最后把部分乘積相加．要把2+3乘以3+，先把2+3乘以3，然后再乘以，最后把部分乘積相加．該過(guò)程讓學(xué)生體會(huì)從特殊的例子當(dāng)中抽象出一般的代數(shù)乘法的運(yùn)算過(guò)程，從而達(dá)到鍛煉學(xué)生思維的目的．

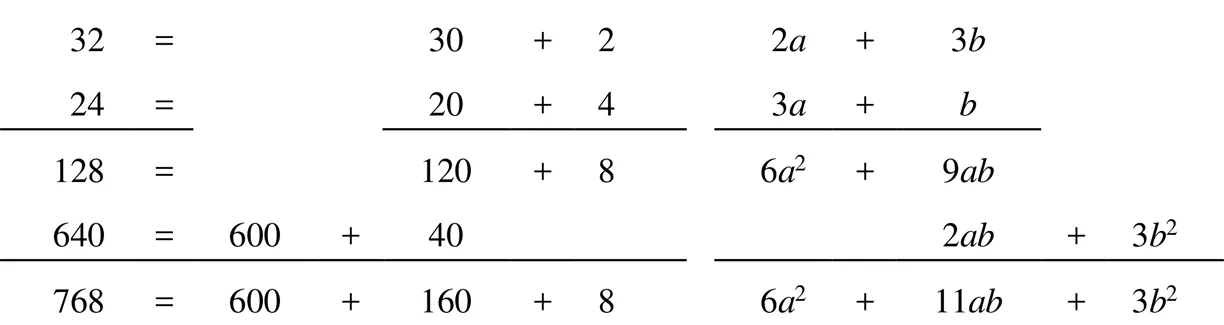
圖4 Lyman多項(xiàng)式乘法運(yùn)算

此外，Gillet認(rèn)為反復(fù)練習(xí)代數(shù)運(yùn)算有助于加強(qiáng)記憶、加快理解，培養(yǎng)精確的習(xí)慣[42]．可見(jiàn)，早期代數(shù)教科書(shū)通過(guò)代數(shù)運(yùn)算來(lái)訓(xùn)練學(xué)生的思維、培養(yǎng)學(xué)生良好的品質(zhì)．

5.2 公式

早期代數(shù)教科書(shū)給出許多物理、工程、商業(yè)等學(xué)科中的公式以及運(yùn)算．Wentworth等寫(xiě)道：“今天任何一種商業(yè)活動(dòng)中，公式都是非常有用的．沒(méi)有公式的知識(shí)、價(jià)值和幫助，一個(gè)人不可能成為商業(yè)領(lǐng)域的真正主人．”[43]可見(jiàn)公式對(duì)于商業(yè)領(lǐng)域的重要性．Schorling等也在其教材中突出強(qiáng)調(diào)公式的結(jié)構(gòu)、意義和使用，認(rèn)為公式作為簡(jiǎn)潔的語(yǔ)言、計(jì)算的簡(jiǎn)寫(xiě)規(guī)則、問(wèn)題的通解、表示一個(gè)量對(duì)另一個(gè)量的依賴關(guān)系的方法[44]．

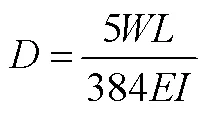
總之，早期代數(shù)教科書(shū)利用公式來(lái)彰顯代數(shù)的實(shí)際應(yīng)用價(jià)值和數(shù)學(xué)的交流價(jià)值．

5.3 方程

方程刻畫(huà)了現(xiàn)實(shí)世界中某些事件所遵循或近似遵循的規(guī)則或定律，是初等代數(shù)的中心問(wèn)題．Myers等認(rèn)為，使用方程的能力是精確思考者的主要裝備，代數(shù)實(shí)質(zhì)上是方程的科學(xué)與藝術(shù)[14]．Kent指出，代數(shù)的主要目的之一是解決用算術(shù)方法難以解決或不可能解決的問(wèn)題，而方程是獲得這些解的手段，事實(shí)上方程是這門(mén)課的中心思想[46]．Young等通過(guò)突出方程在教科書(shū)中的地位來(lái)體現(xiàn)代數(shù)的應(yīng)用價(jià)值[24]．一些教科書(shū)專門(mén)用整章的篇幅來(lái)呈現(xiàn)方程的應(yīng)用，如Taylor分別用一章的篇幅介紹一元一次方程（含6道例題、57道習(xí)題）和一元二次方程（含6道例題、53道習(xí)題）的應(yīng)用[47]．

因此，方程是早期代數(shù)教科書(shū)訓(xùn)練學(xué)生思維能力、凸顯代數(shù)學(xué)科優(yōu)勢(shì)以及實(shí)際應(yīng)用價(jià)值的重要工具之一．

5.4 圖象

通過(guò)圖象能夠直觀地表示出兩個(gè)變量之間的關(guān)系．早期教科書(shū)運(yùn)用函數(shù)圖象或方程曲線，一方面讓學(xué)生通過(guò)觀察圖象了解事物的變化規(guī)律，從而推斷出其中隱含的信息；另一方面讓學(xué)生動(dòng)手操作，繪制圖象并能根據(jù)圖象回答問(wèn)題．

Schorling認(rèn)為，數(shù)學(xué)關(guān)系的圖象表示利用了更廣泛的感官體驗(yàn)．在其它條件相同的情況下，附帶圖象的問(wèn)題容易被更多的學(xué)生理解和欣賞[44]．Schultze等認(rèn)為圖解法不僅有很大的實(shí)用價(jià)值，而且毫無(wú)疑問(wèn)地提供了一種非常好的方法，以防止“學(xué)校代數(shù)退化為一種機(jī)械地應(yīng)用記憶規(guī)則的傾向”[48]．Slaught等列專章介紹圖象表示法[49-50]，其中主要涉及函數(shù)或方程的圖象或圖形．Cajori等用圖象來(lái)表示午后12小時(shí)之內(nèi)的溫度變化情況以及1860—1914年之間美國(guó)無(wú)煙煤價(jià)格的變化情況[51]．Hawkes等在其圖象表示法一章中稱：“商業(yè)世界的科學(xué)數(shù)據(jù)和數(shù)字統(tǒng)計(jì)經(jīng)常以圖象的形式清晰而簡(jiǎn)潔地表示出來(lái)．”[52]

易知，圖象的運(yùn)用可用來(lái)訓(xùn)練學(xué)生的思維能力，激發(fā)學(xué)生的學(xué)習(xí)興趣，并解釋代數(shù)在現(xiàn)實(shí)世界的廣泛應(yīng)用．

5.5 問(wèn)題

這里的問(wèn)題主要指的是文字題，大部分問(wèn)題通常具有一定的學(xué)科背景或?qū)嶋H背景．Lawrence提到：“在代數(shù)教學(xué)方面的經(jīng)驗(yàn)證明，只有把這些原理應(yīng)用到實(shí)際問(wèn)題的解決中，才能使學(xué)生熟悉這些原理．因此，教材中包含大量的實(shí)際例子和問(wèn)題．在選擇這些例子時(shí)，一個(gè)突出的目標(biāo)是選擇那些最有可能使學(xué)生感興趣的，同時(shí)這些例子的解決方案又將加強(qiáng)學(xué)生的分析能力．”[18]有大量的早期代數(shù)教科書(shū)會(huì)用專門(mén)的章節(jié)來(lái)呈現(xiàn)問(wèn)題．例如Day等通過(guò)專門(mén)的章節(jié)來(lái)闡述了代數(shù)在幾何中的應(yīng)用[18，53]，如題“給定了平面三角形的三條邊，求它的面積；一個(gè)人要高出地球表面多高才能看到地球表面的三分之一？”等．Wentworth第十章一共給出了76道練習(xí)題，涉及年齡問(wèn)題、鐘表問(wèn)題、行程問(wèn)題、工程問(wèn)題、圖形面積問(wèn)題、動(dòng)物比賽問(wèn)題、軍事問(wèn)題、經(jīng)濟(jì)問(wèn)題等[54]，可謂豐富多彩．

Durell等[55]認(rèn)為代數(shù)的其它任何部分都不如語(yǔ)言問(wèn)題那樣發(fā)展思想力量和培養(yǎng)對(duì)代數(shù)精神的欣賞．Seaver等指出教材中精心安排了問(wèn)題集，其推理可以很容易地在頭腦中進(jìn)行并通過(guò)口頭表達(dá)出來(lái)．這種口頭使用代數(shù)語(yǔ)言被認(rèn)為是一種非常有效的教學(xué)方法[56]．

可見(jiàn)，早期代數(shù)教科書(shū)在問(wèn)題選擇時(shí)關(guān)注了代數(shù)的學(xué)科基礎(chǔ)、思維訓(xùn)練、實(shí)際應(yīng)用、數(shù)學(xué)交流和情感信念等價(jià)值．

6 結(jié)論與啟示

綜上，1800—1959年間155種美英早期代數(shù)教科書(shū)呈現(xiàn)了7類代數(shù)教育價(jià)值觀，即學(xué)科基礎(chǔ)、思維訓(xùn)練、品質(zhì)培養(yǎng)、實(shí)際應(yīng)用、數(shù)學(xué)交流、情感信念和學(xué)科優(yōu)勢(shì)．在160年間，7類價(jià)值并沒(méi)有呈現(xiàn)出明顯的大起大落現(xiàn)象．由此可見(jiàn)，早期代數(shù)教科書(shū)編寫(xiě)者對(duì)于代數(shù)學(xué)的價(jià)值有著比較全面和客觀的認(rèn)識(shí)．早期教科書(shū)的代數(shù)價(jià)值觀對(duì)今日中學(xué)代數(shù)教學(xué)和教科書(shū)編寫(xiě)具有一定的啟示．

（1）注重代數(shù)的思維訓(xùn)練價(jià)值．早期教科書(shū)中思維訓(xùn)練價(jià)值占了很高的比例，說(shuō)明代數(shù)的學(xué)習(xí)有助于學(xué)生的思維能力發(fā)展．在實(shí)際教學(xué)和教科書(shū)編寫(xiě)時(shí)，要以該價(jià)值的實(shí)現(xiàn)為目標(biāo)，從代數(shù)運(yùn)算、方程求解、問(wèn)題解答等方面出發(fā)，促進(jìn)學(xué)生的積極思考與實(shí)踐，讓學(xué)生的思維真正得到鍛煉．

（2）促進(jìn)代數(shù)與其它學(xué)科的融合．代數(shù)作為學(xué)科基礎(chǔ)這一價(jià)值普遍受到了早期教科書(shū)編寫(xiě)者的關(guān)注，一切需要抽象原理的學(xué)科都離不開(kāi)代數(shù)知識(shí)．在實(shí)際教學(xué)中要讓學(xué)生體會(huì)到代數(shù)這門(mén)學(xué)科的優(yōu)勢(shì)所在，加強(qiáng)與其它學(xué)科的交流，如從公式應(yīng)用、問(wèn)題設(shè)計(jì)等方面著手，讓學(xué)生體會(huì)到代數(shù)在其它學(xué)科發(fā)展中的重要性．

（3）重視代數(shù)學(xué)習(xí)對(duì)學(xué)生的品質(zhì)以及情感信念的影響．學(xué)生一開(kāi)始從算術(shù)思維進(jìn)入代數(shù)思維必定會(huì)遇到一定的困難，教師要注意對(duì)學(xué)生進(jìn)行適當(dāng)?shù)囊龑?dǎo)便于他們能順利渡過(guò)這個(gè)時(shí)期．鼓勵(lì)學(xué)生遇到困難不要退縮，要努力地戰(zhàn)勝困難．在代數(shù)運(yùn)算中培養(yǎng)學(xué)生的專注力、耐力，在問(wèn)題解答中培養(yǎng)學(xué)生獨(dú)立思考、積極進(jìn)取、勇于探索的精神．讓學(xué)生真正體驗(yàn)到學(xué)習(xí)代數(shù)的樂(lè)趣．

（4）加強(qiáng)學(xué)生代數(shù)表達(dá)的訓(xùn)練．代數(shù)語(yǔ)言是一種通用語(yǔ)言，其在訓(xùn)練學(xué)生表達(dá)的精確性和簡(jiǎn)潔性方面起到了決定性的作用．教學(xué)中重視代數(shù)語(yǔ)言的學(xué)習(xí)、加強(qiáng)代數(shù)表達(dá)的訓(xùn)練，一方面能夠有益于學(xué)生邏輯思維的培養(yǎng)，另一方面也便于其它相關(guān)學(xué)科的學(xué)習(xí)．

（5）堅(jiān)持課堂教學(xué)與實(shí)踐相結(jié)合．代數(shù)的實(shí)用價(jià)值表明：數(shù)學(xué)源于生活，又服務(wù)于生活．很多學(xué)生因?yàn)槿狈ι顚?shí)踐，因而對(duì)書(shū)本上的內(nèi)容一知半解．代數(shù)教學(xué)既要挖掘生活素材，又要讓學(xué)生走出課堂，進(jìn)入生活．從公式應(yīng)用、圖象輔助、問(wèn)題設(shè)計(jì)等方面讓學(xué)生感知代數(shù)的實(shí)用價(jià)值，消除代數(shù)無(wú)用的疑慮．這就要求教師從改變課堂教學(xué)方法入手，讓學(xué)生成為課堂的主人，通過(guò)自身的體驗(yàn)感知，從而真正理解數(shù)學(xué)知識(shí)．

[1] Young J W A. The teaching of mathematics in the elementary and the secondary school [M]. New York: Longmans, Green & Co., 1907: 11.

[2] 中華人民共和國(guó)教育部．普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)[M]．北京：人民教育出版社，2018：1-8．

[3] 周琰，譚頂良．學(xué)生數(shù)學(xué)觀發(fā)展?fàn)顩r的調(diào)查研究[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2010，19（4）：27-30．

[4] 謝明初．?dāng)?shù)學(xué)教育的人文追求[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2015，24（1）：6-8．

[5] 周立棟．學(xué)生數(shù)學(xué)意識(shí)養(yǎng)成教育——數(shù)學(xué)教育應(yīng)有的價(jià)值取向[J]．上海教育科研，2010（4）：93-94．

[6] 吳維煊．勿讓“分?jǐn)?shù)場(chǎng)”遮蔽數(shù)學(xué)教育的核心價(jià)值[J]．教育理論與實(shí)踐，2011，31（32）：18-20．

[7] 朱立明，馬云鵬．基于新課標(biāo)的學(xué)生數(shù)學(xué)價(jià)值感悟研究[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2014，23（5）：33-35，55．

[8] 李忠．?dāng)?shù)學(xué)的意義與數(shù)學(xué)教育的價(jià)值[J]．課程·教材·教法，2012，32（1）：58-62．

[9] 王尚志，胡鳳娟．?dāng)?shù)學(xué)教育的育人價(jià)值[J]．人民教育，2018（Z2）：40-44．

[10] 劉鵬飛，孟建偉．論數(shù)學(xué)的人文價(jià)值[J]．自然辯證法研究，2019，35（6）：113-117．

[11] Kelley T L. Values in high school algebra & their measurement [J]. Teachers College Record, 1920, 21(3): 246-290.

[12] Williams J D. An elementary treatise on algebra [M]. Boston: Hilliard, Gray, & Co., 1840: iii-v.

[13] Alsop S. An elementary treatise on algebra [M]. Philadelphia: E. C. & J. Biddle, 1846: 3-11.

[14] Myers G W, Atwood G E. Elementary algebra [M]. Chicago: Scott, Foresman & Company, 1916: 1-6.

[15] Hopkins J W, Underwood P H. Elementary algebra [M]. New York: The Macmillan Company, 1912: vii-viii.

[16] Durell F. Durell’s algebra [M]. New York: Charles E. Merrill Company, 1914: 3-4.

[17] Clarke J B. Algebra for the use of high schools, academies and colleges [M]. San Francisco: A. L. Bancroft and Company, 1881: iii-v.

[18] Lawrence C D. Elements of algebra [M]. New York: Alden, Beardsley & Co., 1853: iii-iv.

[19] Loomis E. Elements of algebra [M]. New York: Harper, 1876: iv.

[20] Green R W. Gradiations in algebra [M]. Philadelphia: I. Ashmead, 1839: v-vii.

[21] Gilbert J H, Sullivan E. Practical lessons in algebra [M]. New York: Richardson, Smith & Company, 1903: iii-iv.

[22] Tower D B. Intellectual algebra [M]. New York: Daniel Burgess, 1855: 3-6.

[23] Bonnycastle J. An introduction to algebra [M]. Philadelphia: Joseph Crukshank, 1806: iii-vii.

[24] Young J W A, Jackson L L. A second course in elementary algebra [M]. New York: D. Appleton and Company, 1910: iii-iv.

[25] Skinner E B. College algebra [M]. New York: The Macmillan Company, 1917: v-vi.

[26] Jones G W. A drill-book in algebra [M]. Ithaca: George W. Jones, 1892: iii-iv.

[27] Wentworth G, Smith D E. Vocational algebra [M]. Boston: Ginn and Company, 1911: iii-iv.

[28] Comstock C E. Elementary algebra [M]. Peoria, Ill.: C. E. Comstock, 1907: 5-7.

[29] Rothrock D A, Whitacre M A. First year algebra [M]. New York: C. Scribner’s Sons, 1932: v-vi.

[30] Dupuis N F. The principles of elementary algebra [M]. New York: The Macmillan Company, 1900: iii-v.

[31] Ford W B. A brief course in college algebra [M]. New York: The Macmillan Company, 1922: v-vi.

[32] Olney E. Introduction to algebra [M]. New York: Sheldon, 1874: 3-4.

[33] Greenleaf B. A practical treatise on algebra [M]. Boston: R. S. Davis and Company, 1852: iii-iv.

[34] Docharty G B. The institutes of algebra [M]. New York: Harper & Brothers, 1867: v-vi.

[35] Hull G W. Elements of algebra for beginners [M]. New York: American Book Company, 1904: 3.

[36] Loomis E. A treatise on algebra [M]. New York: Harper & Brothers, 1846: 10.

[37] Sherwin T. An elementary treatise on algebra [M]. Boston: Sanborn, Carter, Bazin, 1841: 1.

[38] Hotz H G. First year algebra scales: Series a [M]. New York: Teachers College, Columbia University, 1920: 26.

[39] Durell F. Suggestions on the teaching of algebra [M]. New York: Charles E. Merrill Company, 1921: 10-13.

[40] THORNDIKE E L, WOODYARD E, WALD E, et al. The psychology of algebra [M]. New York: The Macmillan Company, 1923: 100-120.

[41] Lyman E A, Darnell A. Elementary algebra [M]. New York: American Book Company, 1917: 74.

[42] Gillet J A. Elementary algebra [M]. New York: H. Holt and Company, 1896: iii-v.

[43] Wentworth G, Schlauch W S, Smith D E. Commercial algebra: Book I [M]. Boston: Ginn, 1917: iii-iv.

[44] Schorling R, Clark J R. Modern algebra: Ninth school year [M]. Yonkers-on-Hudson, N.Y.: World Book Company, 1924: iii-viii.

[45] Stone J C, Millis J F. Elementary algebra: First course [M]. Boston: B. H. Sanborn & Company, 1911: 1-18.

[46] Kent F C. A first course in algebra [M]. New York: Longmans, Green, and Co., 1913: iii-iv.

[47] Taylor J M. Elements of algebra [M]. Boston: Allyn and Bacon, 1900: 99-106, 291-299.

[48] Schultze A, Breckenridge W E. Elementary and intermediate algebra [M]. New York: The Macmillan Company, 1925: v-vi.

[49] Slaught H E, Lennes N J. Elementary algebra [M]. Boston: Allyn and Bacon, 1915: 230-239.

[50] Rietz H L, Taylor E H, Orathorne A R. School algebra: First course [M]. New York: H. Holt and Company, 1915: 180-191.

[51] Cajori F, Odell L R. Elementary algebra [M]. New York: The Macmillan Company, 1915: 16, 63-76.

[52] Hawkes H E, Touton F C, Luby W A. First course in algebra [M]. Boston: Ginn and Company, 1917: 200-210.

[53] Day J, Thomson J B. Elements of algebra [M]. New Haven: Durrie & Peck, 1844: 232-245.

[54] Wentworth G A. Elements of algebra [M]. Boston: Ginn & Heath, 1881: 137-150.

[55] Durell F, Arnold E E. A second book in algebra [M]. New York: C. E. Merrill, 1920: iii-iv.

[56] Seaver E P, Walton G A. The Franklin elementary algebra [M]. Philadelphia: J. H. Butler, 1882: iii-vi.

Educational Values of Algebra in U.S. and English Textbooks Published between 1800 and 1959

SHAO Ai-di1, LIU Si-lu2, WANG Xiao-qin2

(1. Shanghai Yan’an Middle School, Shanghai 200050, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China)

155 kinds of early American and English algebra textbooks published between 1800 and 1959 were selected to examine the content of the prefaces and introductions on the values of algebra education. It was found that the values of algebra education could be divided into seven categories: foundation of discipline, thinking training, character cultivating, practical application, mathematical communication, emotions and beliefs, and advantages of discipline. Taking 20 years as a time period, the seven types of values appeared in different degrees in each time period. This paper analyzes the reflection of values of algebra education in textbooks from five aspects: algebraic operation, formulas, equations, graphs, and problems. It is suggested that today’s middle school algebra teaching and textbook compilation should pay attention to the realization of algebra values.

algebra; educational value; language; thinking; application

G633.62

A

1004–9894（2022）05–0076–06

邵愛(ài)娣，劉思璐，汪曉勤．美英早期代數(shù)教科書(shū)的代數(shù)價(jià)值觀探析[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2022，31（5）：76-81．

2022–07–11

上海高校“立德樹(shù)人”人文社會(huì)科學(xué)重點(diǎn)研究基地之?dāng)?shù)學(xué)教育教學(xué)研究基地研究項(xiàng)目——數(shù)學(xué)課程與教學(xué)中落實(shí)立德樹(shù)人根本任務(wù)的研究（A8）

邵愛(ài)娣（1990—），女，江蘇鹽城人，碩士，主要從事數(shù)學(xué)史與數(shù)學(xué)教育研究．

[責(zé)任編校：陳雋、陳漢君]