試論高中數(shù)學(xué)教師在高中與大學(xué)數(shù)學(xué)銜接中的作用

羅鳳軍，劉 銳

試論高中數(shù)學(xué)教師在高中與大學(xué)數(shù)學(xué)銜接中的作用

羅鳳軍1，劉 銳2

（1．拉薩江蘇實(shí)驗(yàn)中學(xué)，西藏 拉薩 850000；2．南開(kāi)大學(xué) 數(shù)學(xué)科學(xué)學(xué)院/核心數(shù)學(xué)與組合數(shù)學(xué)教育部重點(diǎn)實(shí)驗(yàn)室，天津 300071）

高中與大學(xué)數(shù)學(xué)的銜接問(wèn)題，一直受到眾多學(xué)者的關(guān)注與研究，雖然有很多學(xué)者從大學(xué)教師的角度分析了存在的銜接問(wèn)題及解決措施，但是很少有學(xué)者從高中數(shù)學(xué)教師的角度進(jìn)行研究，尤其是針對(duì)西藏的學(xué)生．因此，結(jié)合眾多研究成果，將西藏的高中數(shù)學(xué)教學(xué)與大學(xué)數(shù)學(xué)教學(xué)進(jìn)行了分析、比較，特別對(duì)高中數(shù)學(xué)教師在高中與大學(xué)數(shù)學(xué)銜接中的作用進(jìn)行了研究，結(jié)果表明：高中數(shù)學(xué)教師通過(guò)合理安排教學(xué)內(nèi)容、創(chuàng)新教學(xué)方式等可以有效促使高中與大學(xué)數(shù)學(xué)更好地銜接．

高中教師；高中數(shù)學(xué)；大學(xué)數(shù)學(xué)；銜接

1 問(wèn)題提出

1.1 研究緣起

2021年9月，經(jīng)中央組織部審核批準(zhǔn)，研究者1（簡(jiǎn)稱(chēng)訪者）有幸成為了一名西藏自治區(qū)2021年“西部之光”訪問(wèn)學(xué)者，走進(jìn)享有“學(xué)府北辰”之美譽(yù)的南開(kāi)大學(xué)進(jìn)行交流訪問(wèn)與學(xué)習(xí)．在此期間，訪者領(lǐng)略了這所百年名校悠久的歷史與厚重的文化，近距離的聆聽(tīng)了大師的精彩授課，感受了名師的魅力與風(fēng)采．在一次數(shù)學(xué)分析課上注意到老師用比較巧妙的方式補(bǔ)充了那一節(jié)需要用到的三角函數(shù)的和差化積公式（學(xué)生在高中沒(méi)有學(xué)過(guò)），課后訪者通過(guò)與老師和學(xué)生的交流及查閱文獻(xiàn)，對(duì)高中數(shù)學(xué)與大學(xué)數(shù)學(xué)銜接問(wèn)題有了更多了解和認(rèn)識(shí)，并與導(dǎo)師一起對(duì)其進(jìn)行了更加深入的研究．

1.2 研究背景及意義

1.2.1 藏族學(xué)生具有的特殊性

毫無(wú)疑問(wèn)，西藏和平解放70年來(lái)，在黨中央、國(guó)務(wù)院的特殊關(guān)懷下，在全國(guó)人民的無(wú)私支援下，在自治區(qū)黨委、政府的堅(jiān)強(qiáng)領(lǐng)導(dǎo)和全區(qū)各族人民的共同努力下，西藏的教育取得了前所未有的巨大進(jìn)步．但是，無(wú)論是從與西藏采用統(tǒng)一試題的其他省份近年來(lái)的高考錄取分?jǐn)?shù)線進(jìn)行對(duì)比，如2021年（見(jiàn)圖1），還是從梁芳老師在“藏區(qū)高中數(shù)學(xué)與大學(xué)數(shù)學(xué)教育銜接中存在的問(wèn)題與對(duì)策”一文中所例舉的，中央民族大學(xué)理學(xué)院藏族班3屆學(xué)生的數(shù)學(xué)高考成績(jī)平均分（最高分只有72分，最低分只有32分）[1]等，全區(qū)的教育與其他地區(qū)相比依舊存在著較大差距，尤其是區(qū)內(nèi)農(nóng)牧區(qū)要遠(yuǎn)落后于市縣，區(qū)外整體落后于其他省份．再加上西藏獨(dú)特的地理環(huán)境（平均海拔在4?000米以上）、語(yǔ)言環(huán)境（藏漢雙語(yǔ)交流）、文化背景（長(zhǎng)期受藏傳佛教影響）及學(xué)生自身（如認(rèn)知水平不高、容易自我封閉）等因素．面臨的高中與大學(xué)數(shù)學(xué)的銜接問(wèn)題更為突出．

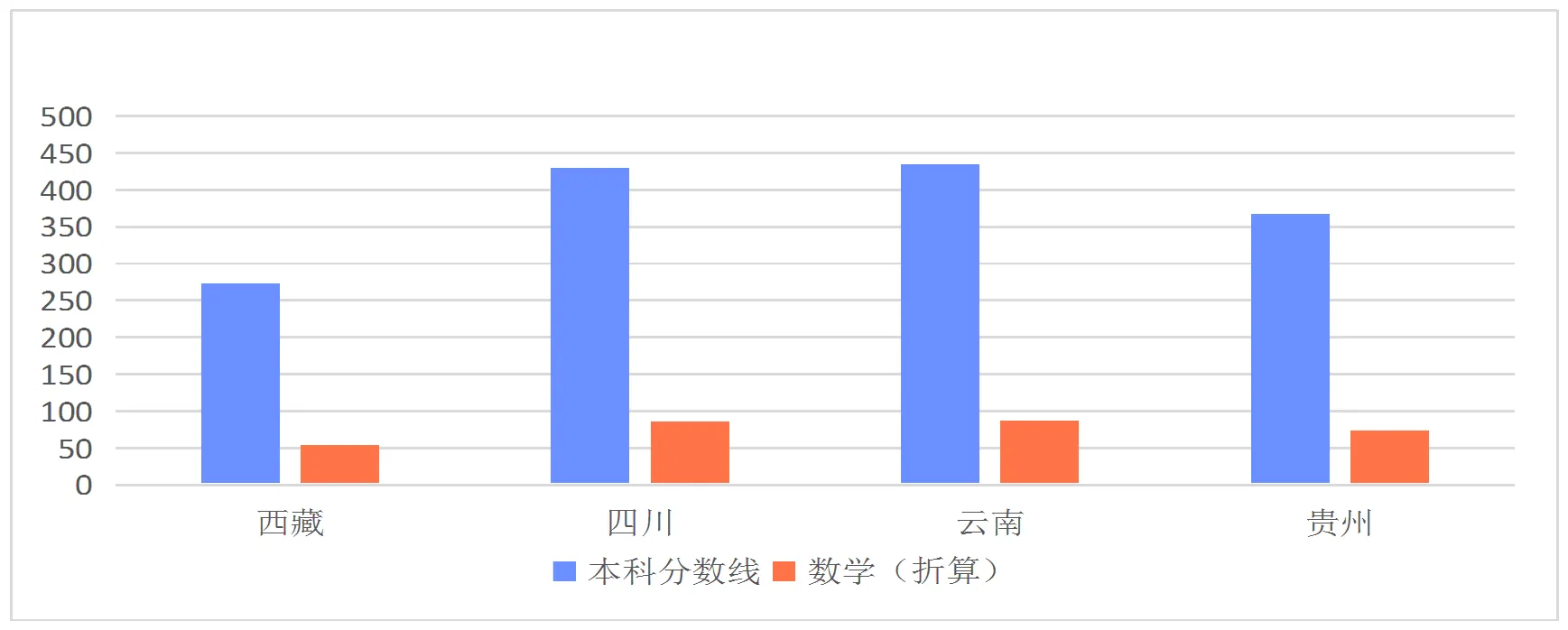
圖1 2021年部分省（區(qū)）理科全國(guó)高考本科錄取分?jǐn)?shù)線柱形圖

1.2.2 現(xiàn)有研究具有的缺失性

高中與大學(xué)數(shù)學(xué)的銜接問(wèn)題一直是國(guó)內(nèi)外許多學(xué)者關(guān)注的熱點(diǎn)．現(xiàn)有的研究中，很多學(xué)者更多地從大學(xué)老師的角度，就教學(xué)內(nèi)容、教學(xué)方法、學(xué)習(xí)方法和學(xué)習(xí)心理等方面分析了高中與大學(xué)數(shù)學(xué)存在的銜接問(wèn)題，并對(duì)大學(xué)老師如何解決存在的銜接問(wèn)題提出了很多解決的辦法．然而，很少有學(xué)者從高中數(shù)學(xué)教師的角度，就高中數(shù)學(xué)教師在高中與大學(xué)數(shù)學(xué)銜接中的作用，尤其是針對(duì)西藏的學(xué)生，提出看法．

從西藏地區(qū)來(lái)看，2015年梁芳老師的“藏區(qū)高中數(shù)學(xué)與大學(xué)數(shù)學(xué)教育銜接中存在的問(wèn)題與對(duì)策”一文，以中央民族大學(xué)理學(xué)院藏族班為例，從兩大方面即：身體心理適應(yīng)、教與學(xué)進(jìn)行了銜接問(wèn)題的探討，并提出了大學(xué)老師應(yīng)該注意語(yǔ)言表達(dá)的規(guī)范性，注意上課的節(jié)奏，增加一些能夠補(bǔ)充高中數(shù)學(xué)的課程等相應(yīng)對(duì)策[1]；2016年拉珍老師在“民族院校藏族大學(xué)生數(shù)學(xué)學(xué)習(xí)困難的成因及對(duì)策分析”中，以拉薩師范高等專(zhuān)科學(xué)校為例，通過(guò)對(duì)拉薩師范高等專(zhuān)科學(xué)校數(shù)學(xué)和自然科學(xué)系2014級(jí)、2015級(jí)8個(gè)班級(jí)的藏族學(xué)生進(jìn)行調(diào)查，分析了藏族大學(xué)生數(shù)學(xué)學(xué)習(xí)困難的成因，并提出高校教師需與中小學(xué)教師加強(qiáng)交流，消除藏族大學(xué)生數(shù)學(xué)學(xué)習(xí)的心理障礙，培養(yǎng)藏族大學(xué)生數(shù)學(xué)自主學(xué)習(xí)能力等對(duì)策[2]．2020年蔡晶的碩士論文“M民族大學(xué)藏族本科生學(xué)習(xí)適應(yīng)性研究”中，通過(guò)對(duì)Ｍ民族大學(xué)113位藏族本科生的問(wèn)卷調(diào)查及15位藏族學(xué)生的深度訪談，了解了藏族本科生在學(xué)習(xí)適應(yīng)中存在的障礙及原因，并進(jìn)一步探究了大學(xué)老師在教學(xué)中要實(shí)現(xiàn)“文化回應(yīng)性教學(xué)”，幫助學(xué)生樹(shù)立正確的能力觀等相應(yīng)的解決措施[3]．

從國(guó)內(nèi)其他地方來(lái)看，2002年10月首都師范大學(xué)王尚志在由教育部高教研究中心委托承辦的“全國(guó)數(shù)學(xué)基礎(chǔ)課程教學(xué)教材改革研討會(huì)”上，呼吁教育界要關(guān)注高中數(shù)學(xué)教學(xué)與大學(xué)數(shù)學(xué)教學(xué)的銜接問(wèn)題[1]；季素月的“高中與大學(xué)數(shù)學(xué)課堂教學(xué)的比較研究”一文，通過(guò)對(duì)學(xué)生學(xué)習(xí)狀況的調(diào)查和個(gè)案分析，對(duì)入學(xué)新生學(xué)習(xí)高等數(shù)學(xué)感到困難的原因作了一些深入的研究與探討，并提出大學(xué)老師需幫助學(xué)生正確地了解和認(rèn)識(shí)自我等建議[4]；潘建輝在“大學(xué)數(shù)學(xué)和新課標(biāo)下高中數(shù)學(xué)的脫節(jié)問(wèn)題與銜接研究”中指出，大學(xué)數(shù)學(xué)教師應(yīng)準(zhǔn)確把握高中數(shù)學(xué)新舊課程的差異，并在對(duì)所授課程與高中新課程銜接內(nèi)容進(jìn)行詳細(xì)對(duì)比的基礎(chǔ)上，采取相應(yīng)的銜接策略[5]；寧連華的“高中數(shù)學(xué)新課程變化內(nèi)容對(duì)大學(xué)數(shù)學(xué)學(xué)習(xí)的影響研究”一文中，指出了大學(xué)新生入學(xué)后的總體適應(yīng)性不高而總體適應(yīng)性程度直接影響大學(xué)數(shù)學(xué)成績(jī)等適應(yīng)性問(wèn)題[6]．

從國(guó)際上來(lái)看，中學(xué)國(guó)際數(shù)學(xué)教育委員會(huì)于1997年11月在英國(guó)的Worthing舉行的會(huì)議上提出“討論中學(xué)到大學(xué)的過(guò)渡以及中學(xué)和大學(xué)間的關(guān)系”[1]．美國(guó)高等教育學(xué)家亞伯拉罕·弗萊克斯納認(rèn)為，中等教育是決定大學(xué)發(fā)展前景和質(zhì)量的基本因素，要建立高水準(zhǔn)的大學(xué)教育，就必須與中等教育達(dá)成一致，注意兩者的銜接[3]．

1.2.3 高中教師參與的重要性

更多研究表明，高中與大學(xué)數(shù)學(xué)銜接存在的問(wèn)題及造成的原因有很多，無(wú)論何種問(wèn)題，有些是客觀造成的，難以避免，但不可否認(rèn)的是，有些還是與高中數(shù)學(xué)教師教學(xué)不當(dāng)有一定的關(guān)系．假若高中數(shù)學(xué)教師在教學(xué)中能夠盡量避免或減少因人為造成的銜接問(wèn)題，不僅可以較好地落實(shí)好“雙減政策”下，如何提高數(shù)學(xué)教學(xué)質(zhì)量的問(wèn)題，而且對(duì)于高中與大學(xué)數(shù)學(xué)銜接問(wèn)題的解決，也會(huì)有很大的促進(jìn)作用．可見(jiàn)，中學(xué)與大學(xué)數(shù)學(xué)的銜接問(wèn)題并不能僅僅依靠大學(xué)教師，中學(xué)數(shù)學(xué)教師也應(yīng)該發(fā)揮積極的作用，促使高中與大學(xué)數(shù)學(xué)更好地銜接．

綜上所述，針對(duì)西藏的學(xué)生，從高中數(shù)學(xué)教師的角度，研究高中與大學(xué)數(shù)學(xué)的銜接是非常有必要的．

1.3 研究問(wèn)題

因此，針對(duì)西藏的學(xué)生（下文中不再?gòu)?qiáng)調(diào)），從高中數(shù)學(xué)教師的角度，結(jié)合西藏的高中數(shù)學(xué)教學(xué)、大學(xué)數(shù)學(xué)教學(xué)和知名學(xué)者們的研究成果，就高中數(shù)學(xué)教師在高中與大學(xué)數(shù)學(xué)銜接中的作用進(jìn)行了研究．現(xiàn)將高中數(shù)學(xué)教師如何合理安排教學(xué)內(nèi)容、創(chuàng)新教學(xué)方式，促使高中與大學(xué)數(shù)學(xué)很好地銜接中發(fā)揮的作用加以論述．供大家參考．

2 問(wèn)題研究

2.1 研究高中數(shù)學(xué)教師在教學(xué)內(nèi)容銜接中的作用

2.1.1 教學(xué)內(nèi)容銜接存在的問(wèn)題

自高中新課標(biāo)實(shí)施以來(lái)，西藏的高中數(shù)學(xué)教材（人教A版普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書(shū)）的內(nèi)容發(fā)生了較大變化[7]．然而，大學(xué)相應(yīng)的一些數(shù)學(xué)教材沒(méi)能根據(jù)高中數(shù)學(xué)教材內(nèi)容的變化做出及時(shí)調(diào)整[8]，再加上高中與大學(xué)老師在教學(xué)中對(duì)知識(shí)的處理情況有差異，從而在高中與大學(xué)數(shù)學(xué)教學(xué)內(nèi)容銜接中自然地出現(xiàn)了部分教學(xué)內(nèi)容有脫節(jié)的情況．具體見(jiàn)如下分析．

（1）重疊知識(shí)的脫節(jié)分析．

高中與大學(xué)數(shù)學(xué)教學(xué)內(nèi)容重疊的知識(shí)，主要是由新課標(biāo)教材引入了大學(xué)數(shù)學(xué)的部分內(nèi)容（比如算法、幾何概型、統(tǒng)計(jì)案例等）及舊教材本身就有的內(nèi)容（如集合、函數(shù)、導(dǎo)數(shù)等）組成[9]．主要有兩種類(lèi)型．① 重疊且一樣型，即高中與大學(xué)的內(nèi)容、形式及要求，基本一致或完全相同．如導(dǎo)數(shù)的引入、常見(jiàn)函數(shù)的導(dǎo)數(shù)、導(dǎo)數(shù)幾何意義、利用導(dǎo)數(shù)判斷函數(shù)的單調(diào)性、研究函數(shù)極值及最值，等等．② 重疊且提升型，即高中與大學(xué)在某一知識(shí)有重疊，但大學(xué)對(duì)該知識(shí)有提升、有補(bǔ)充及要求有變．如集合中在高中補(bǔ)集的基礎(chǔ)上補(bǔ)充了差集的概念等；函數(shù)中對(duì)映射、函數(shù)的定義及最值等性質(zhì)提高了要求；導(dǎo)數(shù)中補(bǔ)充了余切等初等函數(shù)的導(dǎo)數(shù)、對(duì)最值定理給出了證明等等．對(duì)于這部分的內(nèi)容，高中與大學(xué)老師的教學(xué)處理、學(xué)生的學(xué)習(xí)情況都有一定的差異．

首先，在大學(xué)初始階段，部分大學(xué)老師可能會(huì)認(rèn)為學(xué)生對(duì)這些內(nèi)容已經(jīng)掌握或者考慮到重復(fù)講解會(huì)造成學(xué)生的厭煩情緒，通常就不會(huì)再花時(shí)間去講．與此同時(shí)，一部分學(xué)生可能認(rèn)為這些內(nèi)容自己已經(jīng)掌握得很好，就會(huì)對(duì)這部分內(nèi)容的學(xué)習(xí)掉以輕心，再很難以一個(gè)初學(xué)者的姿態(tài)來(lái)認(rèn)真推敲概念、推演公式和進(jìn)行嚴(yán)格論證．

其次，在高中階段，由于受到教師的專(zhuān)業(yè)水平相對(duì)較低、學(xué)生的基礎(chǔ)和理解能力相對(duì)較弱、高中的學(xué)習(xí)基本上以高考為導(dǎo)向等現(xiàn)實(shí)原因，學(xué)生對(duì)高中與大學(xué)重疊內(nèi)容的把握通常沒(méi)有達(dá)到大學(xué)教師的意想．事實(shí)上，對(duì)于高中學(xué)生而言，他們所謂的“掌握”其實(shí)基本上就是一種按部就班、機(jī)械化的訓(xùn)練所形成的固定解題套路，在很大程度上其認(rèn)知仍然停留在“感性認(rèn)知”的層次，處在“知其然而不知其所以然”的狀態(tài)，更沒(méi)能達(dá)到“何由以知其所以然”．長(zhǎng)久如此，勢(shì)必會(huì)對(duì)后續(xù)的學(xué)習(xí)造成不良影響．

（2）斷層知識(shí)的脫節(jié)分析．

高中與大學(xué)數(shù)學(xué)教學(xué)內(nèi)容出現(xiàn)斷層，主要是由于教材的編寫(xiě)、高考的導(dǎo)向及教師的處理不當(dāng)?shù)仍蛟斐傻模渲饕幸韵聝煞N類(lèi)型．

① 人為因素造成的類(lèi)型．雖然教育部門(mén)一再要求教學(xué)內(nèi)容的完整性，但考慮到教育實(shí)際及高考導(dǎo)向等原因，部分高中教師對(duì)學(xué)生比較難理解的知識(shí)（如函數(shù)的概念及部分性質(zhì)、向量的線性運(yùn)算、立體幾何等）或高考中很少涉及的知識(shí)（如數(shù)學(xué)歸納法、反證法、推理方法等），還是存在教學(xué)中對(duì)其降低學(xué)習(xí)要求或刪減教學(xué)的情況．當(dāng)然這是大學(xué)教師很難預(yù)料到的，自然也就不會(huì)再講．

② 教材因素造成的類(lèi)型．這種類(lèi)型主要有3種情況：其一，有些在大學(xué)數(shù)學(xué)學(xué)習(xí)中需要用到的基礎(chǔ)知識(shí)，在高中必修教材中卻被刪除或降低了要求（如極限、反函數(shù)、三角函數(shù)的余切、正割、余割、和差化積、反三角函數(shù)等），高中老師自然地不會(huì)深講或補(bǔ)充；其二，文理教材存在差異（如計(jì)數(shù)原理、排列與組合、二項(xiàng)定理、空間向量等在文科系列教材中被刪除），文科學(xué)生就會(huì)有沒(méi)學(xué)過(guò)的知識(shí)；其三，選修系列內(nèi)容存在差異，從選修4-4（坐標(biāo)系與參數(shù)方程）與選修4-5（不等式選講）中選修一門(mén)，導(dǎo)致有些學(xué)生只知其中一門(mén)知識(shí)的情況．然而，學(xué)生在高中沒(méi)有學(xué)過(guò)的內(nèi)容，其大多在大學(xué)教材中又沒(méi)有編寫(xiě)或被放到了預(yù)備知識(shí)部分一筆帶過(guò)．再加上大學(xué)老師受授課時(shí)間的限制和對(duì)高中教材熟悉情況的影響，一些大學(xué)教師對(duì)這部分內(nèi)容的處理通常比較倉(cāng)促，有些甚至?xí)患咏榻B就直接拿來(lái)用．

因此，部分學(xué)生在大學(xué)數(shù)學(xué)的學(xué)習(xí)中，容易出現(xiàn)在高中沒(méi)有接觸過(guò)而在大學(xué)也沒(méi)有學(xué)（或?qū)W會(huì)）的知識(shí)即斷層知識(shí)，自然地，學(xué)生知識(shí)結(jié)構(gòu)上就可能會(huì)出現(xiàn)一些相應(yīng)的漏洞，也會(huì)對(duì)大學(xué)數(shù)學(xué)的學(xué)習(xí)有一定程度的影響．

2.1.2 教學(xué)內(nèi)容銜接問(wèn)題的解決措施

針對(duì)以上高中與大學(xué)數(shù)學(xué)教學(xué)內(nèi)容銜接存在的問(wèn)題，高中數(shù)學(xué)教師可以通過(guò)以下方式，合理安排教學(xué)內(nèi)容，促使高中與大學(xué)數(shù)學(xué)較好地銜接．

（1）不斷學(xué)習(xí)努力提高，奠定內(nèi)容銜接基礎(chǔ)．

工欲善其事，必先利其器．為了使高中與大學(xué)的數(shù)學(xué)教學(xué)內(nèi)容自然銜接．作為高中數(shù)學(xué)教師，在認(rèn)真做好日常教學(xué)工作的同時(shí)，還有必要通過(guò)自學(xué)、培訓(xùn)、進(jìn)修、訪學(xué)等途徑溫故或研修部分大學(xué)數(shù)學(xué)內(nèi)容（尤其是數(shù)學(xué)系幾門(mén)入門(mén)課，比如數(shù)學(xué)分析，高等代數(shù)和解析幾何等）．

或許，有的老師可能認(rèn)為大學(xué)數(shù)學(xué)與高中數(shù)學(xué)或者高考沒(méi)什么直接的關(guān)系，日常教學(xué)工作本身就比較繁重（非常能理解這一點(diǎn)），還花心思去學(xué)那些完全就是浪費(fèi)功夫和精力．

其實(shí)不然．首先，這一過(guò)程不僅可以使高中教師消化領(lǐng)會(huì)高中與大學(xué)數(shù)學(xué)重疊的知識(shí)，在教學(xué)中能夠更好的將這些知識(shí)傳授給學(xué)生，以此不斷完善他們的知識(shí)結(jié)構(gòu)，而且能夠提升教師自身專(zhuān)業(yè)水平與素養(yǎng)．于訪者而言，這次訪學(xué)受益非淺，不僅在專(zhuān)業(yè)知識(shí)、教研能力得到進(jìn)一步提高，而且價(jià)值觀、人生觀、世界觀也得到更加的完善．這次訪學(xué)交流無(wú)疑是一次學(xué)術(shù)和思想的雙重成長(zhǎng)與歷練，必將會(huì)為其今后的教學(xué)工作與生活注入新的思路與活力．

其次，高中數(shù)學(xué)教師，其中部分雖然學(xué)習(xí)過(guò)新納入高中教材的高中與大學(xué)重疊的知識(shí)，但由于可能較長(zhǎng)時(shí)間沒(méi)有使用，已經(jīng)遺忘；另外也可能存在一部分老師，根本就沒(méi)有學(xué)習(xí)過(guò)這些內(nèi)容．不管如何，要想把自己也沒(méi)能消化與掌握的內(nèi)容傳授給學(xué)生，恐怕是不太現(xiàn)實(shí)的．

再次，高中數(shù)學(xué)教師若能對(duì)大學(xué)數(shù)學(xué)有進(jìn)一步的認(rèn)識(shí)和了解，就能夠更好地比較高中與大學(xué)數(shù)學(xué)的一些內(nèi)容，梳理好高中與大學(xué)數(shù)學(xué)重疊及斷層的知識(shí)，明確這部分內(nèi)容在高中與大學(xué)的差異．在此基礎(chǔ)上，老師們?cè)诮虒W(xué)中就能更好地做好教學(xué)內(nèi)容的銜接，為學(xué)生大學(xué)的學(xué)習(xí)打下扎實(shí)的基礎(chǔ)．

（2）據(jù)其特點(diǎn)因時(shí)制宜，促使教學(xué)內(nèi)容銜接．

針對(duì)重疊的類(lèi)型及人為因素造成的斷層類(lèi)型而出現(xiàn)教學(xué)內(nèi)容脫節(jié)情況．高中數(shù)學(xué)教師在教學(xué)中，首先，要按照《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》（簡(jiǎn)稱(chēng)《課程標(biāo)準(zhǔn)》），做到不隨意刪減教學(xué)內(nèi)容或降低學(xué)習(xí)要求，力爭(zhēng)將高中數(shù)學(xué)知識(shí)完整地傳授給學(xué)生，盡可能地避免人為造成高中與大學(xué)數(shù)學(xué)知識(shí)出現(xiàn)斷層[10-11]．其次，還有必要明確告知學(xué)生雖然高中與大學(xué)數(shù)學(xué)有一些知識(shí)重疊的現(xiàn)象，但是絕大部分內(nèi)容在廣度和深度上有明顯差異，特別是有些在高中數(shù)學(xué)中還不大可能給出嚴(yán)格論證的結(jié)論（如最大最小值定理的證明），不妨先告訴學(xué)生利用大學(xué)數(shù)學(xué)的哪些內(nèi)容（大概率是微積分）就能給出一個(gè)簡(jiǎn)單優(yōu)美的證明，而這些大都會(huì)在學(xué)了一定程度的大學(xué)數(shù)學(xué)之后變得明朗，使得對(duì)于整個(gè)高中數(shù)學(xué)也大有“一覽眾山小”之感．不容置疑的是，這樣做（即告訴學(xué)習(xí)大學(xué)數(shù)學(xué)的哪些知識(shí)可以徹底澄清他們高中階段可能存在的疑惑）必然會(huì)讓一些學(xué)生帶著在高中的困惑與對(duì)大學(xué)數(shù)學(xué)的憧憬與渴望去學(xué)習(xí)大學(xué)數(shù)學(xué)，也就為認(rèn)真研習(xí)大學(xué)數(shù)學(xué)埋下了伏筆．

針對(duì)教材因素造成的斷層類(lèi)型而出現(xiàn)教學(xué)內(nèi)容脫節(jié)的情況．高中數(shù)學(xué)教師要善于抓住恰當(dāng)?shù)臅r(shí)機(jī)，采用合理的方法，對(duì)知識(shí)做必要的拓展和補(bǔ)充，盡最大努力補(bǔ)齊可能會(huì)出現(xiàn)斷層的知識(shí)，盡可能地使高中數(shù)學(xué)與大學(xué)數(shù)學(xué)無(wú)縫銜接．

如何補(bǔ)齊？首先，高中必修教材中被刪除或降低了要求的內(nèi)容，就如三角函數(shù)的余切、正割、余割可作為拓展知識(shí)處理（見(jiàn)圖2）．課上，在講解正弦、余弦、正切定義同時(shí)也可以給學(xué)生介紹余切、正割、余割的定義．課后，讓學(xué)生借助幾何畫(huà)板作圖、觀察、總結(jié)或通過(guò)關(guān)于3者的研究性學(xué)習(xí)活動(dòng)、撰寫(xiě)數(shù)學(xué)小論文的方式來(lái)了解3者的圖象及性質(zhì)．并告知學(xué)生這3個(gè)三角函數(shù)在高中雖然沒(méi)有要求學(xué)習(xí)，但是在大學(xué)會(huì)用到，而且這一補(bǔ)充并不需要花費(fèi)多少功夫，也不會(huì)給學(xué)生造成什么困擾．這樣做，不僅可以促使學(xué)生拓展數(shù)學(xué)知識(shí)、完善知識(shí)結(jié)構(gòu)及補(bǔ)齊知識(shí)漏洞，也提高了學(xué)生的動(dòng)手能力、撰寫(xiě)能力及多媒體的應(yīng)用能力，對(duì)學(xué)生主動(dòng)學(xué)習(xí)意識(shí)、自主學(xué)習(xí)能力的提升有不可估量的促進(jìn)作用．

其次，文理教材存在差異的內(nèi)容，在文科教學(xué)中可以適當(dāng)滲透一些理科知識(shí)．比如，給文科學(xué)生介紹如何用計(jì)數(shù)原理、排列與組合的知識(shí)解決古典概型，如何用空間向量解決立體幾何問(wèn)題，等等．

再次，選修系列內(nèi)容存在差異，最好是要求所有學(xué)生將兩門(mén)選修課程都加以學(xué)習(xí)．這樣一來(lái)，不僅能夠讓學(xué)生在高考中針對(duì)兩道題的難易情況，選擇自己最有把握的題目進(jìn)行作答提高分?jǐn)?shù)，而且對(duì)于如何解決好這方面的銜接有一定的作用．

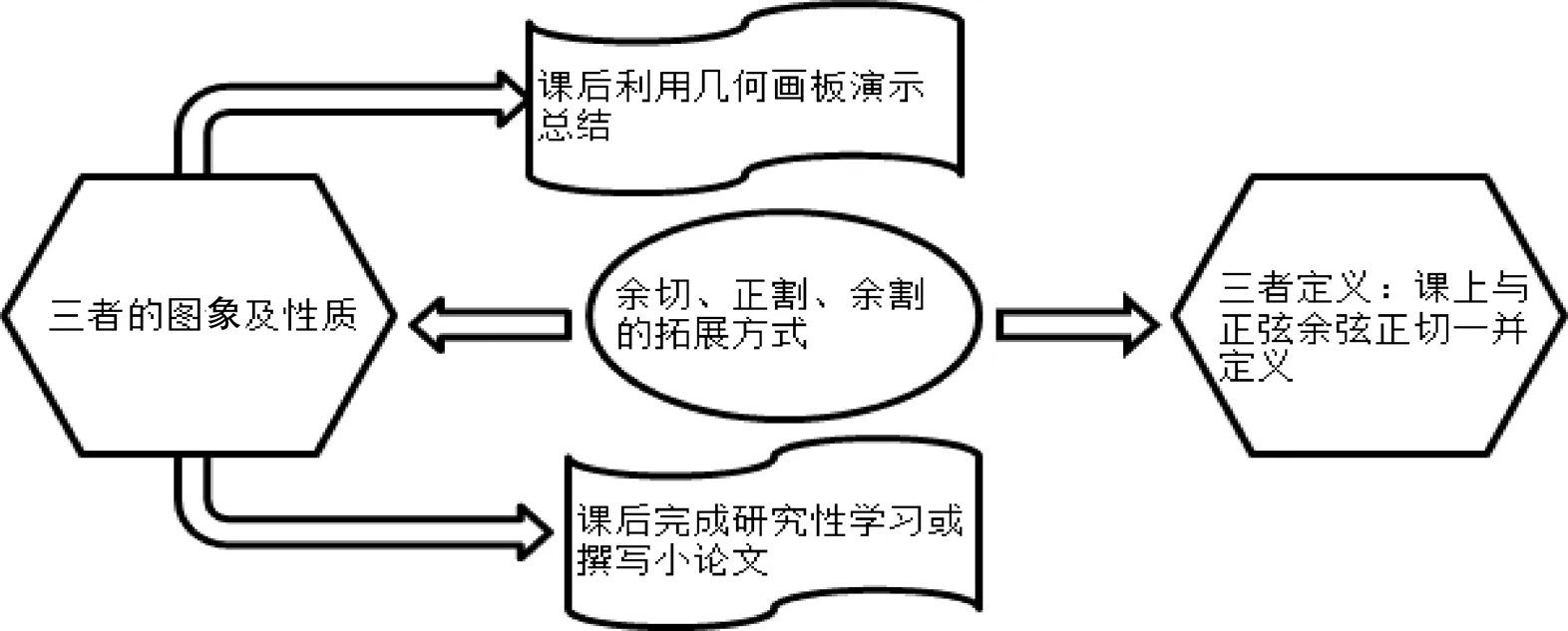
圖2 三角函數(shù)“余切正割余割”的拓展方式示意

2.2 研究高中數(shù)學(xué)教師在教學(xué)方式銜接中的作用

2.2.1 教學(xué)方式銜接存在的問(wèn)題

隨著西藏新課改的不斷深入，高中數(shù)學(xué)課堂教學(xué)形式多樣、師生互動(dòng)頻繁，教學(xué)內(nèi)容較少、簡(jiǎn)單、直觀，在知識(shí)教授中偏重于命題結(jié)論及其應(yīng)用而不太注重知識(shí)的探究過(guò)程，教學(xué)過(guò)于重技巧與分?jǐn)?shù)而減少了能力與素養(yǎng)的培養(yǎng)．而大學(xué)數(shù)學(xué)課堂教學(xué)形式相對(duì)比較單一、課上師生互動(dòng)通常較少，教學(xué)內(nèi)容較多、抽象、系統(tǒng)，在知識(shí)教授中命題的論證過(guò)程與結(jié)論并重、能力與技巧并重，屬于思想方法與能力素養(yǎng)并重的素質(zhì)教育．可見(jiàn)，高中與大學(xué)數(shù)學(xué)教學(xué)方式存在一定的差異，自然地，也就會(huì)出現(xiàn)以下一些銜接問(wèn)題．

（1）首先，雖然西藏全域已實(shí)現(xiàn)雙語(yǔ)教育，但是學(xué)生的漢語(yǔ)水平還是比較低且養(yǎng)成了用藏語(yǔ)思維考慮數(shù)學(xué)問(wèn)題的習(xí)慣，進(jìn)入大學(xué)后，隨著語(yǔ)言環(huán)境的變化就容易出現(xiàn)一定的語(yǔ)言障礙；其次，由于特殊的地理環(huán)境及高中數(shù)學(xué)教學(xué)節(jié)奏比較慢等原因，學(xué)生比較習(xí)慣慢節(jié)奏的學(xué)習(xí)．自然地，學(xué)生不能較好地跟上大學(xué)數(shù)學(xué)老師知識(shí)講解較快的節(jié)奏，也不能完全聽(tīng)明白老師教授的內(nèi)容．

（2）西藏采用的是傳統(tǒng)的高考模式，考試與錄取之間的聯(lián)系只有分?jǐn)?shù)．既受“唯分?jǐn)?shù)論”和“一考定終身”的影響，又考慮到學(xué)生數(shù)學(xué)基礎(chǔ)較差、數(shù)學(xué)理解能力不強(qiáng)、學(xué)習(xí)自覺(jué)性不高等原因，擔(dān)心學(xué)生學(xué)不會(huì)．從而高中課堂教學(xué)內(nèi)容較少，課上基本圍繞一個(gè)知識(shí)點(diǎn)反復(fù)講解和練習(xí)，課下配套同類(lèi)習(xí)題進(jìn)行鞏固和強(qiáng)化．學(xué)生只要按照老師的要求，課上認(rèn)真聽(tīng)講，課后反復(fù)練習(xí)，就能較好地掌握好數(shù)學(xué)知識(shí)并能取得較為理想的成績(jī)．可見(jiàn)，高中數(shù)學(xué)教學(xué)基本上還是以高考為導(dǎo)向的應(yīng)試教育，這就較容易造成學(xué)生“高分低能”、數(shù)學(xué)素養(yǎng)較低、學(xué)習(xí)較為被動(dòng)等后果．

相對(duì)來(lái)說(shuō)，首先，由于學(xué)生數(shù)學(xué)基礎(chǔ)較差、數(shù)學(xué)能力和數(shù)學(xué)素養(yǎng)較低等原因，當(dāng)學(xué)生面對(duì)大學(xué)數(shù)學(xué)教學(xué)從高中有限的直觀數(shù)學(xué)變化到抽象的、無(wú)窮的數(shù)學(xué)，學(xué)習(xí)內(nèi)容豐富了許多，課上通常會(huì)針對(duì)多個(gè)知識(shí)點(diǎn)進(jìn)行講解，雖然也有促進(jìn)理解的練習(xí)，但是與高中相比要少很多等變化，學(xué)生會(huì)感到不適，在課上通常難以通透所有的知識(shí)．其次，一方面學(xué)生為了更好地通透大學(xué)數(shù)學(xué)教學(xué)內(nèi)容，只有課后按照老師的要求自主學(xué)習(xí)，才能加深對(duì)概念和定理的理解和掌握，學(xué)生在學(xué)習(xí)上需降低對(duì)老師的依賴(lài)，需要的是一種更為主動(dòng)的現(xiàn)代化的學(xué)習(xí)方式；另一方面學(xué)生有一定的語(yǔ)言障礙，容易自我封閉，不能很好地完成與漢族學(xué)生交流并開(kāi)展合作學(xué)習(xí)，然而大學(xué)的很多學(xué)習(xí)內(nèi)容需要學(xué)生共同完成．基于這兩方面原因，當(dāng)進(jìn)入大學(xué)后，學(xué)習(xí)需由接受式學(xué)習(xí)轉(zhuǎn)向自主式學(xué)習(xí)，在短時(shí)間內(nèi)，大部分學(xué)生可能很難完成從“被動(dòng)學(xué)習(xí)”到“自主學(xué)習(xí)”的轉(zhuǎn)變．

（3）雖然學(xué)生具有開(kāi)朗、活潑、熱情、淳樸的性格特征和吃苦耐勞的精神，且能歌善舞，但由于學(xué)生自身存在一些不利因素：數(shù)學(xué)基礎(chǔ)較差、學(xué)習(xí)主動(dòng)性不高、學(xué)習(xí)認(rèn)知水平較低、學(xué)習(xí)適應(yīng)能力較差等，并且高中教育基本還是以高考為導(dǎo)向，也就容易忽視思想教育．當(dāng)較多學(xué)生感覺(jué)大學(xué)與中學(xué)數(shù)學(xué)的教學(xué)方式存有一定差異很不適應(yīng)時(shí)，并沒(méi)能主動(dòng)地去解決，而更多地想依賴(lài)?yán)蠋煟欢@往往不太容易實(shí)現(xiàn)．這就使得他們不斷地感受到大學(xué)數(shù)學(xué)越學(xué)越枯燥、抽象、難懂，學(xué)習(xí)數(shù)學(xué)的興趣與熱情也隨之不斷降低．還有，學(xué)生還比較容易滿(mǎn)足和懈怠，由于家人等過(guò)分地強(qiáng)調(diào)高考的重要性，使部分學(xué)生歷經(jīng)十幾年的寒窗苦讀實(shí)現(xiàn)大學(xué)夢(mèng)后，誤以為人生目標(biāo)已達(dá)成，從而出現(xiàn)短暫的目標(biāo)迷失、學(xué)習(xí)迷失、價(jià)值迷失等．自然而然地產(chǎn)生在大學(xué)數(shù)學(xué)起始階段容易退縮或沒(méi)能認(rèn)真學(xué)習(xí)的現(xiàn)象．

當(dāng)然，可能還存在其它問(wèn)題．無(wú)論何種問(wèn)題，有些是客觀造成的，難以避免，但高中數(shù)學(xué)老師尚可從其它方面入手去做一些事情，以促使更好地銜接．

2.2.2 教學(xué)方式銜接問(wèn)題的解決措施

針對(duì)以上高中與大學(xué)數(shù)學(xué)教學(xué)方式銜接存在的問(wèn)題，高中數(shù)學(xué)教師可以通過(guò)以下措施，創(chuàng)新教學(xué)方式，促使高中與大學(xué)數(shù)學(xué)更好地銜接．

（1）深化數(shù)學(xué)能力培養(yǎng)，提高數(shù)學(xué)核心素養(yǎng)．

知識(shí)誠(chéng)可貴，素養(yǎng)價(jià)更高．針對(duì)學(xué)生“高分低能”、數(shù)學(xué)思維不是很高、不太容易適應(yīng)大學(xué)初始階段的數(shù)學(xué)學(xué)習(xí)的問(wèn)題，深化數(shù)學(xué)能力培養(yǎng)，提高數(shù)學(xué)核心素養(yǎng)不失為一種有效且具有重大意義的舉措．作為高中數(shù)學(xué)教師，在教學(xué)中應(yīng)該認(rèn)識(shí)到數(shù)學(xué)核心素養(yǎng)與數(shù)學(xué)知識(shí)相比，前者是“隱性”，后者是“顯性”．考試所取得的成績(jī)是暫時(shí)的，而培養(yǎng)所得的數(shù)學(xué)核心素養(yǎng)是融進(jìn)血液，伴隨終身的．?dāng)?shù)學(xué)核心素養(yǎng)是數(shù)學(xué)學(xué)科的靈魂，也是學(xué)生科學(xué)思想與能力實(shí)現(xiàn)進(jìn)一步成長(zhǎng)的前提基礎(chǔ)和沃土，其在學(xué)生加深對(duì)知識(shí)的理解和能力的提升方面會(huì)形成難以估量的強(qiáng)大拉力．由此可觀，培養(yǎng)學(xué)生數(shù)學(xué)核心素養(yǎng)之意義，是何等之重大[11-13]．

那么，具體如何去培養(yǎng)呢？首先要認(rèn)真解讀并領(lǐng)會(huì)《課程標(biāo)準(zhǔn)》關(guān)于技能與能力的要求：“通過(guò)高中數(shù)學(xué)課程的學(xué)習(xí)，使學(xué)生獲得進(jìn)一步學(xué)習(xí)及未來(lái)發(fā)展所必需的數(shù)學(xué)基礎(chǔ)知識(shí)、基本技能、基本思想、基本活動(dòng)經(jīng)驗(yàn)（簡(jiǎn)稱(chēng)‘四基’）；提高從數(shù)學(xué)角度發(fā)現(xiàn)和提出問(wèn)題的能力、分析和解決問(wèn)題的能力（簡(jiǎn)稱(chēng)‘四能’）”及關(guān)于數(shù)學(xué)核心素養(yǎng)的要求“在學(xué)習(xí)數(shù)學(xué)和應(yīng)用數(shù)學(xué)的過(guò)程中，學(xué)生能發(fā)展數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、數(shù)學(xué)運(yùn)算、直觀想象、數(shù)據(jù)分析等數(shù)學(xué)學(xué)科核心素養(yǎng)”[10]．然后，在教學(xué)中，牢牢地抓住落實(shí)好“四基”和“四能”并最終實(shí)現(xiàn)“三會(huì)”（會(huì)用數(shù)學(xué)的眼光觀察世界，會(huì)用數(shù)學(xué)的思維思考世界，會(huì)用數(shù)學(xué)的語(yǔ)言表達(dá)世界）[11]這一數(shù)學(xué)核心素養(yǎng)培養(yǎng)主線，既要強(qiáng)化解題技能提高學(xué)生分?jǐn)?shù)，盡力幫助學(xué)生順利考入理想的大學(xué)，也要深化數(shù)學(xué)能力培養(yǎng)提高數(shù)學(xué)核心素養(yǎng)，使學(xué)生具備能夠進(jìn)一步學(xué)習(xí)大學(xué)數(shù)學(xué)的基本數(shù)學(xué)能力和基本數(shù)學(xué)素養(yǎng)．為使大家能夠更好地應(yīng)用于教學(xué)，這里列舉兩例略加說(shuō)明．

例一：通過(guò)注重概念教學(xué)落實(shí)培養(yǎng)．正如高中教材主編章建躍所說(shuō)：“概念教學(xué)是數(shù)學(xué)教學(xué)的重中之重，而得出數(shù)學(xué)概念的過(guò)程是最典型的數(shù)學(xué)抽象過(guò)程．”[13]然而，在高中教學(xué)中教師往往會(huì)忽視這一點(diǎn)．

比如，集合概念的教學(xué)，由于高考中集合的概念不會(huì)直接考察，從而就會(huì)出現(xiàn)輕視集合概念教學(xué)的情況．但事實(shí)上，集合這一概念至關(guān)重要，它在數(shù)學(xué)中幾乎是無(wú)處不在不可或缺的．這不僅僅是因?yàn)閿?shù)學(xué)所考慮的對(duì)象基本上都是某些集合，同時(shí)因?yàn)榧线€是數(shù)學(xué)表述的基本語(yǔ)言．毫不夸張地說(shuō)，集合之于數(shù)學(xué)，無(wú)異于文字之于文章，面粉之于饅頭．這也是為什么集合是高中數(shù)學(xué)學(xué)習(xí)中的第一個(gè)概念．因?yàn)榧僭O(shè)沒(méi)有集合這一概念，恐怕后面很多內(nèi)容將無(wú)法展開(kāi)，或者很難展開(kāi)．可想而知，如何自然地在學(xué)生頭腦中建立起集合的概念，對(duì)于高中數(shù)學(xué)后續(xù)知識(shí)的學(xué)習(xí)、數(shù)學(xué)學(xué)習(xí)興趣的培養(yǎng)與信心的提高都至關(guān)重要．

因此，在教學(xué)中應(yīng)該通過(guò)多列舉一些學(xué)生熟悉的事例（如1—10之間的所有偶數(shù)，班里所有的學(xué)生，所有的正方形等），讓學(xué)生通過(guò)逐步探究慢慢地構(gòu)建出集合的概念（具體教學(xué)可參考圖3自行補(bǔ)充）．這樣一來(lái)，不僅達(dá)到了集合教學(xué)中“四基”及“四能”的落實(shí)，而且也讓學(xué)生在探究集合概念的過(guò)程中，不斷地培養(yǎng)了數(shù)學(xué)抽象、直觀想象等數(shù)學(xué)核心素養(yǎng)．

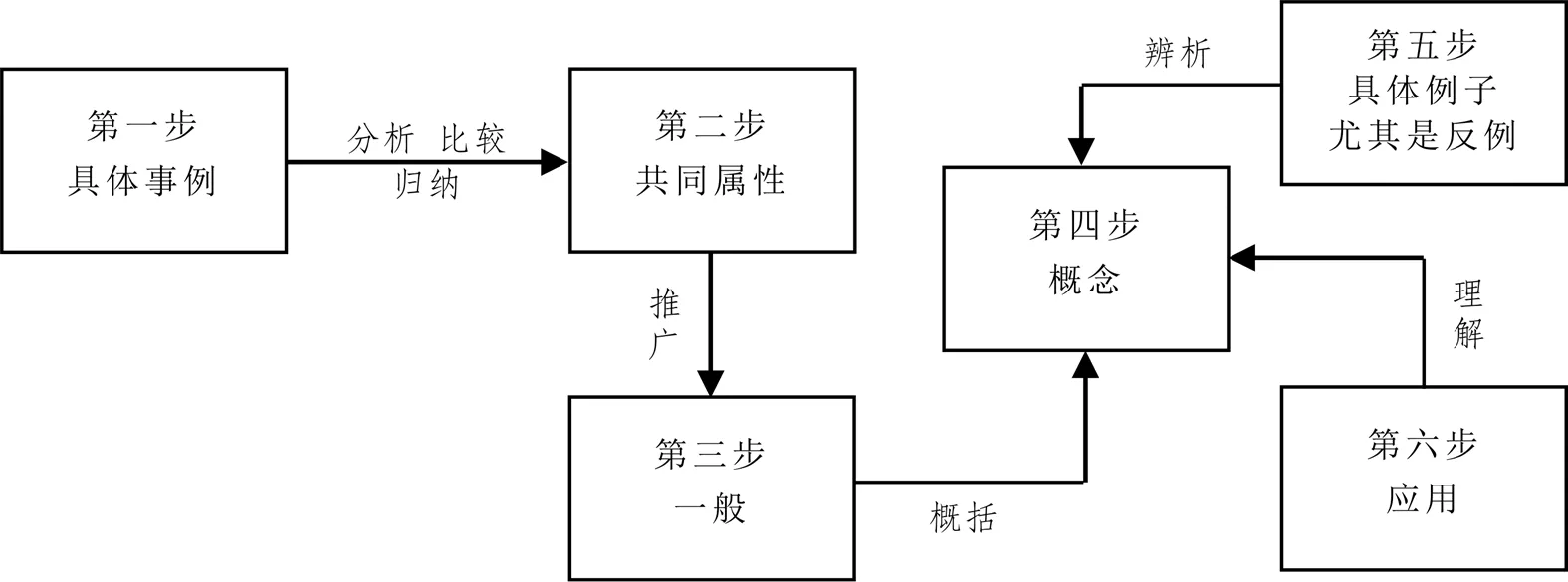
圖3 培養(yǎng)學(xué)生數(shù)學(xué)抽象等核心素養(yǎng)的概念教學(xué)流程

例二：通過(guò)注重試題講解落實(shí)培養(yǎng)．這樣，不僅能夠使學(xué)生感受試題中數(shù)學(xué)核心素養(yǎng)的評(píng)價(jià)方式，而且也通過(guò)刷題鞏固基礎(chǔ)知識(shí)、強(qiáng)化解題技能的同時(shí)，培養(yǎng)了學(xué)生數(shù)學(xué)核心素養(yǎng)．當(dāng)然，教師一定要注意教授方式，就如曹廣福所說(shuō)：“不管高考怎么命題，數(shù)學(xué)教學(xué)僅靠‘刷題’和‘套路’都是不行的，必須認(rèn)真思考如何真正培養(yǎng)學(xué)生的數(shù)學(xué)思維能力．要培養(yǎng)學(xué)生的思維能力，關(guān)鍵不是呈現(xiàn)解題步驟，而是講清楚并讓學(xué)生體會(huì)到解題思路．為此，數(shù)學(xué)教學(xué)要傳授數(shù)學(xué)思想，努力達(dá)成‘應(yīng)試’與‘素質(zhì)’的平衡．”[14]

解析：①

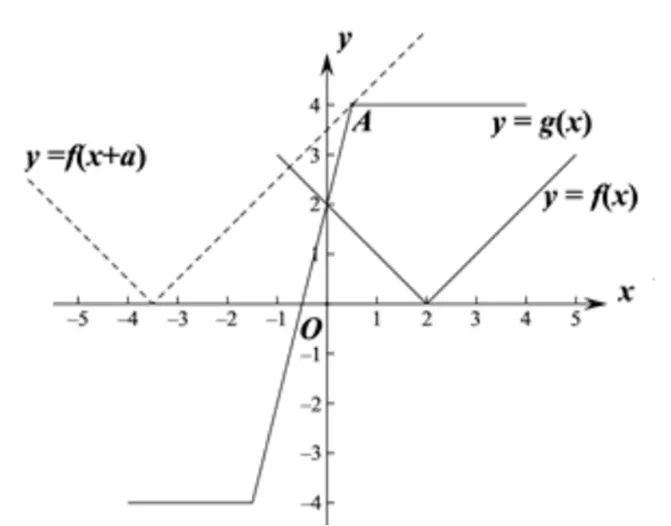
圖4 函數(shù)圖象

小結(jié)：該題通過(guò)考查絕對(duì)值函數(shù)圖象的畫(huà)法及不等式恒成立問(wèn)題等相關(guān)知識(shí)，滲透數(shù)形結(jié)合、分類(lèi)討論、轉(zhuǎn)化與化歸等數(shù)學(xué)思想方法，從而有效考查直觀想象、邏輯推理、數(shù)學(xué)運(yùn)算等數(shù)學(xué)核心素養(yǎng)．在教學(xué)中，遵循“不斷摸索、試錯(cuò)、猜想、檢驗(yàn)”這一解決問(wèn)題的過(guò)程，通過(guò)創(chuàng)設(shè)一系列引導(dǎo)式問(wèn)題為導(dǎo)向、組織合適的活動(dòng)為載體，啟發(fā)學(xué)生尋找解決問(wèn)題的思路，并組織學(xué)生分析和解決問(wèn)題[15]．

（2）滲透數(shù)學(xué)課程思政，踐行立德樹(shù)人使命．

澆花要澆根，育人先育心．針對(duì)如何改變學(xué)生學(xué)習(xí)大學(xué)數(shù)學(xué)知難而退、學(xué)習(xí)興趣不高及如何正確樹(shù)立三觀而好好學(xué)習(xí)大學(xué)初始階段的數(shù)學(xué)的問(wèn)題，滲透數(shù)學(xué)課程思政，踐行立德樹(shù)人使命是非常有必要的．作為高中數(shù)學(xué)教師，應(yīng)該認(rèn)識(shí)到對(duì)學(xué)生過(guò)分強(qiáng)調(diào)題海戰(zhàn)術(shù)和數(shù)學(xué)計(jì)算而忽略數(shù)學(xué)思想方法的歸納、總結(jié)與數(shù)學(xué)知識(shí)結(jié)構(gòu)的梳理，雖然短時(shí)間內(nèi)可能提高學(xué)生一定的數(shù)學(xué)成績(jī)，但這種教學(xué)方式不僅違反了“德育為先、能力為重”這一教育目標(biāo)，而且會(huì)在一定程度上摧殘學(xué)生心智，從長(zhǎng)遠(yuǎn)來(lái)看這無(wú)異于揠苗助長(zhǎng)舍本求末，將會(huì)使學(xué)生很難適應(yīng)更高學(xué)段的學(xué)習(xí)．

如何育人？正如習(xí)近平總書(shū)記在學(xué)校思想政治理論課教師座談會(huì)上所說(shuō)：“挖掘其它課程和教學(xué)方式中蘊(yùn)含的思想政治教育資源，實(shí)現(xiàn)全員全程全方位育人．”在教學(xué)中依照《課程標(biāo)準(zhǔn)》，抓住數(shù)學(xué)課程思政這個(gè)抓手，充分挖掘高中數(shù)學(xué)教材及試卷中蘊(yùn)含的思政元素，并選擇適當(dāng)?shù)臅r(shí)機(jī)，采取合理的方式將其融入到課堂，把數(shù)學(xué)知識(shí)傳授、能力與素養(yǎng)培養(yǎng)、思政教育有機(jī)結(jié)合起來(lái)（如表1）．從而，不但踐行了高中數(shù)學(xué)教學(xué)承載著知識(shí)傳授、能力培養(yǎng)、提高素養(yǎng)及立德樹(shù)人根本任務(wù)，也使原本繁雜枯燥的課堂更具趣味性，不斷激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣、增強(qiáng)信心和可持續(xù)發(fā)展性，也樹(shù)立了學(xué)生敢于質(zhì)疑、善于思考、嚴(yán)謹(jǐn)求實(shí)的科學(xué)精神及正確的人生觀、世界觀、價(jià)值觀，養(yǎng)成終身學(xué)習(xí)的習(xí)慣．自然地，在他們面對(duì)大學(xué)期間更加抽象和豐富的數(shù)學(xué)知識(shí)的時(shí)候也就會(huì)無(wú)所畏懼、迎難而上．

表1 西藏高中數(shù)學(xué)教材（試題）中的部分思政元素[16]

（3）注重以學(xué)生為主體，培養(yǎng)學(xué)生自主學(xué)習(xí)．

授人以魚(yú)，不如授人以漁．針對(duì)學(xué)生習(xí)慣用藏語(yǔ)思維考慮數(shù)學(xué)問(wèn)題、沒(méi)有良好的學(xué)習(xí)習(xí)慣和自主學(xué)習(xí)能力不高而難以較快適應(yīng)大學(xué)初始階段的數(shù)學(xué)學(xué)習(xí)的問(wèn)題．正如著名數(shù)學(xué)家華羅庚所說(shuō)：“一切創(chuàng)作發(fā)明，都不是靠別人教會(huì)的，而是靠自己想，自己做，不斷取得進(jìn)步．”因此，高中數(shù)學(xué)教師，在教學(xué)中依照《課程標(biāo)準(zhǔn)》所說(shuō)：“學(xué)生是數(shù)學(xué)學(xué)習(xí)的主人，教師是數(shù)學(xué)學(xué)習(xí)的組織者、引導(dǎo)者與合作者．”[10]要把學(xué)習(xí)的主動(dòng)權(quán)交還給學(xué)生．通過(guò)引導(dǎo)學(xué)生課前閱讀教材、查閱資料等學(xué)會(huì)課前預(yù)習(xí)；鼓勵(lì)學(xué)生大膽質(zhì)疑，帶著問(wèn)題上課，課上要求學(xué)生用漢語(yǔ)與老師和同學(xué)交流與探討，提高漢語(yǔ)表達(dá)能力且教會(huì)學(xué)生怎么聽(tīng)課；課后自己梳理、歸納、總結(jié)知識(shí)、獨(dú)立完成作業(yè)及撰寫(xiě)反思教會(huì)學(xué)生自檢自練等優(yōu)化學(xué)習(xí)的方式．促使學(xué)生養(yǎng)成自主學(xué)習(xí)和獨(dú)立思考的習(xí)慣，實(shí)現(xiàn)由“學(xué)會(huì)”知識(shí)轉(zhuǎn)變?yōu)椤皶?huì)學(xué)”知識(shí)．這樣一來(lái)，學(xué)生進(jìn)入大學(xué)后就能較快適應(yīng)，也使其受益終生[17]．

3 研究展望

（1）感悟育人提高教學(xué)質(zhì)量，打牢基礎(chǔ)促成銜接．

或許大家依舊存疑，那就不妨走進(jìn)人教版小學(xué)語(yǔ)文課文“桃花心木”中（建議讀者看看原文）．文章講述的是林清玄先生在故鄉(xiāng)看到的一個(gè)種樹(shù)人的故事，其大體意思是：每當(dāng)種樹(shù)人把樹(shù)苗種下以后，他常來(lái)澆水．奇怪的是，他來(lái)得并沒(méi)有規(guī)律，有時(shí)隔3天，有時(shí)隔5天，有時(shí)十幾天才來(lái)一次．澆水的量也不一定，有時(shí)澆得多，有時(shí)澆得少．更奇怪的是，桃花心木苗有時(shí)莫名其妙地枯萎了，他來(lái)的時(shí)候總會(huì)帶幾株樹(shù)苗來(lái)補(bǔ)種．開(kāi)始作者覺(jué)得種樹(shù)人太懶，才這樣澆水沒(méi)有規(guī)律．后來(lái)與種樹(shù)人交談后，才明白了其中的道理．種樹(shù)人說(shuō)：“種樹(shù)不是種菜或種稻子，種樹(shù)是百年的基業(yè)，不像青菜幾個(gè)星期就可以收成．所以，樹(shù)木自己要學(xué)會(huì)在土里找水源．我澆水只是模仿老天下雨，老天下雨是算不準(zhǔn)的，它幾天下一次？上午或下午？一次下多少？如果無(wú)法在這種不確定中汲水生長(zhǎng)，樹(shù)苗自然就枯萎了．但是，在不確定中找到水源、拼命扎根的樹(shù)，長(zhǎng)成百年的大樹(shù)就不成問(wèn)題了．”

仁者見(jiàn)仁，智者見(jiàn)智．這一故事，在教書(shū)育人上能給研究者很多深刻的啟發(fā)，值得大家慢慢去尋味其中蘊(yùn)含的道理．并將其與教學(xué)實(shí)際相結(jié)合，不斷提高教學(xué)質(zhì)量，為高中與大學(xué)數(shù)學(xué)的銜接打下扎實(shí)的基礎(chǔ)．

（2）搭建平臺(tái)加強(qiáng)合作交流，共同解決銜接問(wèn)題．

當(dāng)然，研究者也清醒地認(rèn)識(shí)到，關(guān)于高中教師在高中與大學(xué)數(shù)學(xué)銜接中的更多作用，還有待不斷地被發(fā)現(xiàn)．因此，希望通過(guò)對(duì)這方面的研究，實(shí)現(xiàn)以下愿望．

首先，希望有更多的研究者能夠關(guān)注高中教師在高中與大學(xué)數(shù)學(xué)銜接中的作用，尤其是針對(duì)少數(shù)民族學(xué)生．堅(jiān)信，隨著研究的深入，會(huì)有更多具有實(shí)效性、可操作性的解決辦法出現(xiàn)，促使高中與大學(xué)數(shù)學(xué)更好地銜接的同時(shí)，也對(duì)少數(shù)民族地區(qū)教育質(zhì)量的提高起到一定的促進(jìn)作用．

其次，正如全國(guó)政協(xié)委員田剛所說(shuō)：“高中和高校是兩個(gè)截然不同的教育階段，進(jìn)入大學(xué)意味著挑戰(zhàn)和壓力．如何更好地加深高中、大學(xué)在人才培養(yǎng)、教育貫通等方面的互動(dòng)交流，實(shí)現(xiàn)學(xué)校之間的銜接過(guò)渡，應(yīng)該受到廣泛關(guān)注．”在此，呼吁有關(guān)教育主管部門(mén)，繼續(xù)為高中與大學(xué)之間搭建更多的平臺(tái)，能使更多的高中教師走入大學(xué)提高自己，也使更多的大學(xué)老師走入高中指導(dǎo)教學(xué)與科研，通過(guò)交流與合作促使雙方相互了解相互促進(jìn)，為高中與大學(xué)的銜接發(fā)揮各自應(yīng)有的作用，共同為實(shí)現(xiàn)中華民族偉大復(fù)興的中國(guó)夢(mèng)輸送人才、貢獻(xiàn)力量．

[1] 梁芳．藏區(qū)高中數(shù)學(xué)與大學(xué)數(shù)學(xué)教育銜接中存在的問(wèn)題與對(duì)策——以中央民族大學(xué)理學(xué)院藏族班為例[J]．中央民族大學(xué)學(xué)報(bào)（自然科學(xué)版），2015（2）：64–68．

[2] 拉珍．民族院校藏族大學(xué)生數(shù)學(xué)學(xué)習(xí)困難的成因及對(duì)策分析——以拉薩師范高等專(zhuān)科學(xué)校為例[J]．西部素質(zhì)教育，2016，2（13）：8–9．

[3] 蔡晶．M民族大學(xué)藏族本科生學(xué)習(xí)適應(yīng)性研究[D]．北京：中央民族大學(xué)，2020：2–3．

[4] 季素月，錢(qián)林．大學(xué)與中學(xué)數(shù)學(xué)學(xué)習(xí)銜接問(wèn)題的研究[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2000，9（4）：45–49．

[5] 潘建輝．大學(xué)數(shù)學(xué)和新課標(biāo)下高中數(shù)學(xué)的脫節(jié)問(wèn)題與銜接研究[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2008，17（2）：67–69．

[6] 寧連華，顧鋒，何曉敏，等．高中數(shù)學(xué)新課程變化內(nèi)容對(duì)大學(xué)數(shù)學(xué)學(xué)習(xí)的影響研究[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2014，23（4）：16–20．

[7] 課程教材研究所，中學(xué)數(shù)學(xué)課程教材研究開(kāi)發(fā)中心．普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書(shū)·數(shù)學(xué)[M]．北京：人民教育出版社，2005：2–12．

[8] 劉春根，朱少紅，李軍，等．高等學(xué)校教材·數(shù)學(xué)分析（上冊(cè)）[M]．北京：高等教育出版社，2015：1–20．

[9] 趙莎．高中數(shù)學(xué)與數(shù)學(xué)分析銜接問(wèn)題的研究[D]．西寧：青海師范大學(xué)，2019：5–16．

[10] 中華人民共和國(guó)教育部．普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）[M]．北京：人民教育出版社，2018：2–8．

[11] 史寧中．高中數(shù)學(xué)課程標(biāo)準(zhǔn)修訂中的關(guān)鍵問(wèn)題[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2018，27（1）：8–10．

[12] 路江江，王亞妮．高中數(shù)學(xué)教育中如何培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)——王尚志教授訪談錄[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2021，30（2）：67–70．

[13] 章建躍．樹(shù)立課程意識(shí)落實(shí)核心素養(yǎng)[J]．?dāng)?shù)學(xué)通報(bào)，2016，55（5）：1–4，14．

[14] 曹廣福．新高考背景下的數(shù)學(xué)教學(xué)散思[J]．教育研究與評(píng)論（中學(xué)教育教學(xué)版），2021（6）：5–8．

[15] 朱清波，曹廣福．例談探究式解題課教學(xué)[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2020，29（2）：49–52．

[16] 何恩榮，黃永明，葉丹．課程思政視角下的中學(xué)數(shù)學(xué)教學(xué)研究[J]．求知導(dǎo)刊，2020（29）：66–68．

[17] 方祥兵．新課改下如何培養(yǎng)高中生學(xué)習(xí)數(shù)學(xué)的自學(xué)能力[J]．中學(xué)課程輔導(dǎo)（教學(xué)研究），2021（28）：28．

On the Role of High School Mathematics Teachers in the Connection between High School and University Mathematics

LUO Feng-jun1, LIU Rui2

(1. Jiangsu Experimental Middle School in Lhasa, Tibet Lhasa 850000,China;2. School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071, China)

The connection issue of mathematics between senior high schools and universities has given rise to many scholars’ attentions and research. Though many experts have analyzed the existing connection problems and solutions from the perspective of university teachers, few experts have carried out research from the perspective of high school mathematics teachers, especially few research on students in Tibet. Therefore, this paper analyzes and compares the mathematics teaching in high schools in Tibet and in universities; besides, the research on the role of teachers in the connection process between high schools and universities has been emphasized by the combination of many research achievements. It finds out that high school mathematics teachers caneffectively promote the connection by arranging the content of courses properly and innovate teaching methods, etc.

high school teachers; high school mathematics; university mathematics; connection

G632

A

1004–9894（2022）05–0041–07

羅鳳軍，劉銳．試論高中數(shù)學(xué)教師在高中與大學(xué)數(shù)學(xué)銜接中的作用[J]．?dāng)?shù)學(xué)教育學(xué)報(bào)，2022，31（5）：41-47．

2022–05–25

中組部、教育部西部之光訪問(wèn)學(xué)者資助項(xiàng)目（2021）；西藏自治區(qū)教育科學(xué)研究2020年度立項(xiàng)課題——西藏中學(xué)生數(shù)學(xué)核心素養(yǎng)的培養(yǎng)研究（XZJYKTDWZZ08）；南開(kāi)大學(xué)2022年本科教育教學(xué)改革項(xiàng)目——數(shù)學(xué)基礎(chǔ)課程的課程思政建設(shè)與實(shí)踐研究——以《泛函分析》課程改革為例（NKJG2022053）；國(guó)家自然科學(xué)基金面上項(xiàng)目（12071230，11971348，11671214）；南開(kāi)大學(xué)百名青年學(xué)科帶頭人經(jīng)費(fèi)項(xiàng)目（63213027，91923104，91823003，63174012）；中央高校基本科研業(yè)務(wù)費(fèi)專(zhuān)項(xiàng)基金（63191503，63171225）

羅鳳軍（1978—），男，彝族，云南大理人，中教高級(jí)，主要從事高中數(shù)學(xué)教育教學(xué)研究．劉銳為本文通訊作者．

[責(zé)任編校：周學(xué)智、張楠]