“研趣”學習：實現學生數學思維進階的應然追尋
——以“三角形‘變形計’”一課為例

江蘇省南京市百家湖小學 王 軍 黃德忠

有關三角形的面積練習中有這樣一道題目（見圖1）引起了筆者的注意。這道練習題的設計意圖是讓學生通過在平行線之間畫出兩個與指定三角形面積相等但形狀不同的三角形來感受三角形的等積變形。對于這道練習題的教學處理，教師往往止步于“等底等高”的三角形面積相等的結論，使學生的數學思維和空間觀念的發展比較有限。因此，筆者從圖形運動變化的視角出發，對這道練習素材進行了更為深入的發掘和處理，與學生開展了以“三角形‘變形計’”為研究主題的探究活動課，以期激發學生數學學習的研究樂趣和達成深度學習目標。

圖1

一、教學過程

師（出示課題：三角形“變形計”）：同學們，今天我們要學習的內容與三角形有關，你們會算它的面積嗎？

生1：底×高÷2。

師：回到課題，猜一猜，我們今天會變三角形的什么呢？

生：可能會變三角形的形狀、底、高、面積或者周長。

師：有這么多的可能，看來今天這節課會有點意思。那咱們就一同走進“變形”的世界吧。

師：看，同學們能利用掌握的知識求出涂色部分的面積嗎？（見圖2）

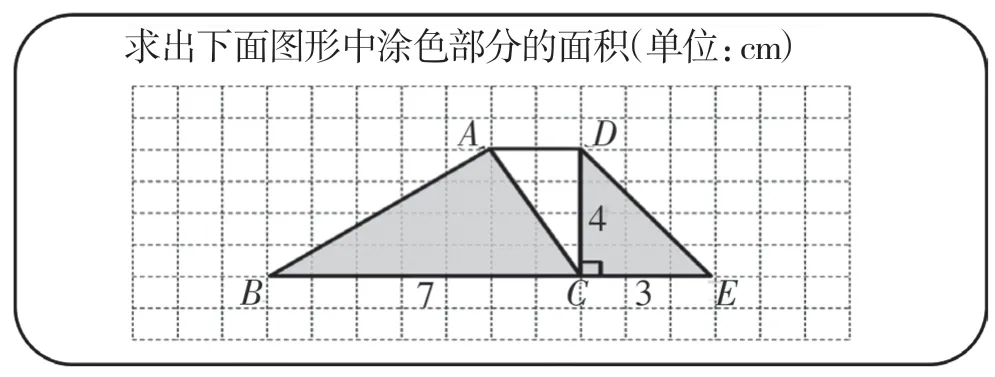
圖2

師：同學們解決了嗎？誰來分享一下你的解答過程？

生2：先算直角三角形DCE的面積是3×4÷2=6（平方厘米），再算三角形ABC的面積是7×4÷2=14（平方厘米），最后算出面積和是6+14=20（平方厘米）。

師：你怎么知道三角形ABC中BC邊上的高是4厘米？

生3：因為AD與BE是相互平行的，DC是三角形DCE中CE邊上的高，垂直于CE，因此，DC的長度就是三角形ABC的高的長度。

師：原來是利用了平行線之間的距離處處相等的特征。其實，在這里，這個距離就是三角形ABC和三角形DCE底邊上的高。

師： 能利用學過的知識解決問題，真聰明。同學們還有不一樣的方法嗎？

生4：我是這樣解決的，連接AE，那么大三角形ABE的面積就是原來兩個小三角形的面積和，因此，面積和就是（7＋3）×4÷2=20（平方厘米）。

師：方法很奇特！誰能理解他的解題方法？

生5：他的方法其實就是將三角形DEC的D點向左平移運動到A點，將三角形DCE變成三角形ACE，然后和三角形ABC合并成大三角形ABE。

師：你們倆的方法是這個意思嗎？請大家觀察在D點移到A點的過程中，三角形DCE變成三角形ACE后，什么變了？什么沒變？

生6：底沒變，都是以CE為底，高的長度也沒變。

生7：三角形DCE變成三角形ACE后形狀變了，但是面積沒變。

師：那你們現在能解釋為什么三角形ABE和陰影部分的面積和相等？

生8：三角形DCE與三角形ACE同底等高，所以面積相等。因此三角形ABE可以看成兩個小三角形的面積和，與陰影部分的面積和相等。

師：有意思，一個點的移動就給我們解決問題帶來了這么大的方便。那這里會移動的點還藏著什么奧秘呢？下面，我們一起來研究下面的探究活動（見圖3）。

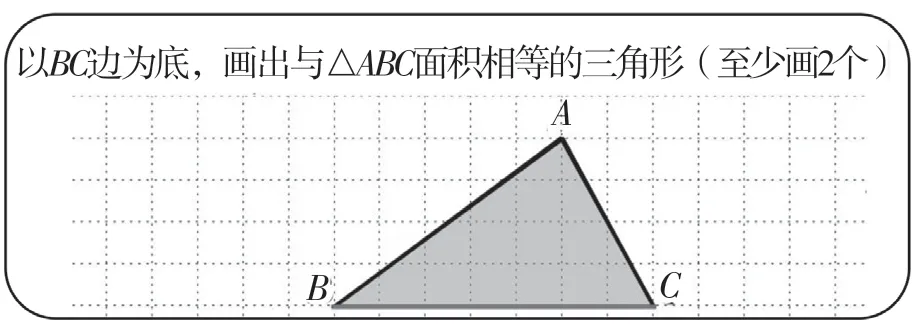
圖3

（學生自主畫圖操作，教師巡視并指導。3分鐘后，全班交流）

師：這幾名同學畫的三角形都符合要求嗎？

生9：它們的底相同，都是BC邊；高的長度相等，都是4厘米。所以面積都相等。

師：像這樣以BC為底，高相等的三角形還有嗎？

生10：有，還可以畫出很多。請大家看我畫的作品。（見圖4）

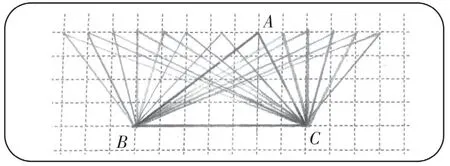
圖4

師：畫出了這么多的三角形？觀察一下，什么變了？什么沒變？

生11：三角形的形狀變了，面積沒變；高的位置變了，底的位置沒變。

師：真棒，你的數學眼光真敏銳。請同學們仔細觀察這幾名同學的作品，說說有什么發現。

生12：我發現其實就是三角形的頂點A在移動，而底邊BC保持不變。

師：有意思，只是一個頂點A在移動。那A點除了我們畫出來的這些位置，還能移動到哪兒呢？

生13：我發現符合要求的點都在過A點且與BC邊平行的一條直線上移動。

師：為什么在這條直線上移動就能保證面積相等呢？

生14：首先底邊BC不變，底是相同的，而頂點在這條平行線上移動，高的長度也會保持不變。同底等高的三角形面積相等。

師：原來這里還是利用了平行線之間的距離處處相等。

師：只能移動A點畫面積相等的三角形嗎？觀察思考一下，還可以怎樣？試著把你的想法在圖上畫出來。

學生代表的作品依次呈現：（見圖5）

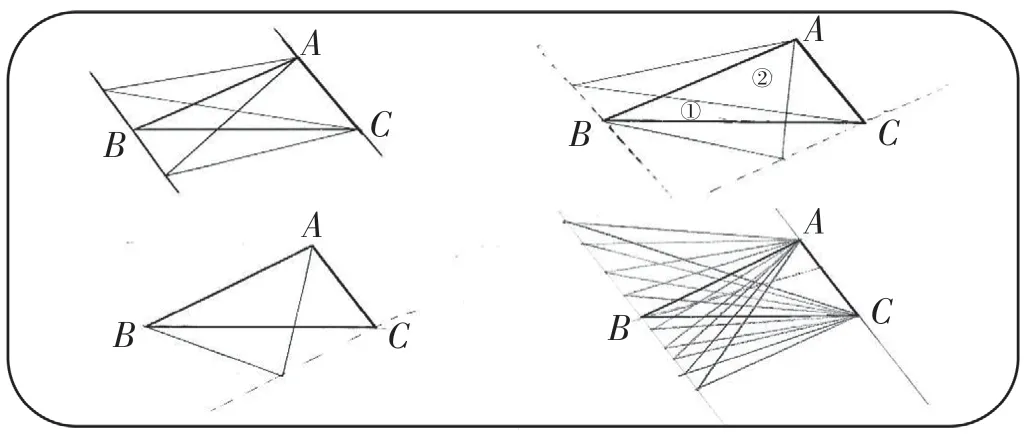
圖5

師：誰來說一說只要怎樣畫就可以？

生15：過B點或C點作對邊的平行線，在平行線上任意取一點，都可以畫出面積相等的三角形。

師：原來我們可以像這樣任意移動三角形的一個頂點，都能畫出無數個面積相等的三角形。

師：通過剛才的探究活動，相信同學們對三角形的“變形”有了一定的認識。帶著我們的發現，回到一開始的問題，你們現在能解釋那名同學解決問題的奇特方法了嗎？誰再來解釋一下。

（學生嘗試解釋。教師呈現移點合并的動畫過程）

師：除了將D點移動到A點，還可以怎么移動？

生16：可以將A點移動到D點，也可以將A點和D點同時向中間移動。

師：在剛才的學習過程中，你們有什么發現？

生17：都是在平行線上移動頂點把兩個三角形合成一個底為10厘米、高為4厘米的三角形。

師：那這里合并后三角形的頂點其實就是原來的A點？D點？AD點？其實也可以是新的名字——F點。

師：俗話說：“合久必分，分久必合。”剛剛研究了“合”，我們再來看看“分”的情況。

師：看，這就是我們一開始遇見分成兩個三角形的情況。（動畫演示）（見圖6）

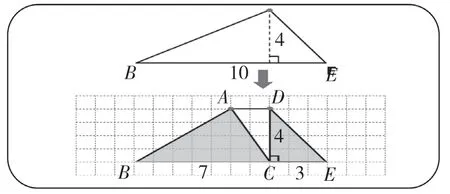
圖6

師：通過剛才的研究，我們知道上下兩個圖形的面積是一樣的。

師：請大家想象一下在大三角形的這個頂點里真的只能包含兩個點，分成兩個三角形嗎？

生18：還可以分成三個三角形，四個三角形，無數個三角形。

師：那我們一起來看一看分成三個三角形的情況。（動畫演示）（見圖7）

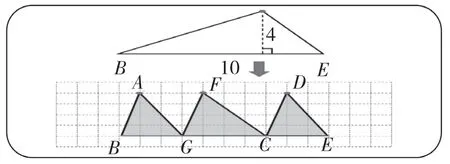
圖7

師：誰能把這三個點還原回去驗證一下面積變了沒有？

（引導學生利用同底等高、移動頂點合并三角形的方式還原成一個三角形）

師：還可以怎么分？請同學們自己畫一畫。

師：誰來說一說怎么驗證面積不變？

（學生小組交流，嘗試運用動點合并的方式驗證面積不變）

師（小結）：無論分成多少個三角形，面積總是不變的。

師：同學們，一個原本圖形中靜止不動的點就這樣被我們給玩“活”了。它里面竟然包含著這么多的數學智慧。我們還可以怎么研究三角形的“變形”？

生19：還可以研究三角形的底。

師：除了研究三角形之外，還能研究什么圖形？

生20：還能研究長方形、平行四邊形、梯形、多邊形。

師：是的，我們還可以研究很多圖形。更多的奧秘就留給你們課后自己去探索吧。

二、教學反思

（一）設計“研趣”活動，優化深度學習的思維歷程

發展學生的空間觀念需要教師有效利用探究素材和組織活動激發學生的學習動機，并讓學生充分經歷觀察、比較和思考的研究過程，通過動態變換和空間想象的手法促使學生對圖形的認識從靜態固化逐步過渡到動態變化，從而讓學生把握圖形與幾何知識學習的本質。在教學中，筆者將常態下的三角形面積問題進行了有機改造和適度延伸，引導學生經歷了 “動點巧解面積問題—尋找等積變形的動點軌跡—三角形的分解與合并”的趣味學習活動，使學生深入體會用運動變化的觀點認識和思考三角形及其變化方式、圖形與圖形之間的關系等。同時，筆者有意識地將學生畫出的變式三角形進行有序整合，促使學生借助觀察這種運動變化中的“瞬間圖形”思考和聯想其中更多的變化和規律。因此，這樣充滿研究樂趣的學習歷程不僅有利于激發學生的學習動機，打破學生意識中原有的靜止、絕對的空間觀念，還有利于在潛移默化中幫助學生自然而然地建立起動態、變化的空間觀念，真正實現數學深度學習。

（二）創生“研趣”氛圍，導引思維可視的學習進階

教師在運用動態手法進行教學的過程中，應適時地給學生提供應用知識的機會，尤其是讓學生進行數學思維的可視化表達，將自己內隱的、潛在的思維過程通過外顯、直觀的創生活動表達出來。這不僅有利于課堂生成更多有價值的資源及展現學生獲取知識的思維過程，還有利于激發學生積極主動地完善對知識的理解，形成動態化的分析思路。在教學中，筆者精心安排了讓學生自主畫圖操作的創生活動。學生一個個充分發揮想象力和創造力，巧手設計三角形的變形分解與合并。在充滿研究樂趣的創生活動中，學生不但設計出大三角形分解成四個、五個、六個小三角形的變形情況，還想象推斷出其能分解成無限個小三角形，并且能靈活運用點的運動來進行逆向的還原合并。所以，這種直觀物化與動態想象相結合的創生活動，不僅促進了學生運用運動變化的觀點進行學習探索，還使學生在分析、思考和理解三角形變形分解與合并的同時，感受到了事物之間存在的“靜止到運動、絕對到相對、有限到無限、量變到質變”的辯證思想，實現了數學學習的進階。因此，動態思路的建立不僅有助于學生更加靈活地分析和處理圖形與幾何領域中的有關問題，還將推動學生的思維發展。

（三）凸顯“研趣”價值，聚焦問題解決的思維本質

在教學中，學生的注意力和思維力不能僅僅停留在圖形表面的變化上。教師應引導學生從聯系的視角出發，在圖形運動變化的過程中，觀察、分析和思考其中的不變因素，歸納總結其本質規律，形成結構化的知識圖譜。這樣，學生便能擺脫細節的羈絆，從全局上分析問題的本質，形成從整體上把握的一種數學思維方式。在教學中，筆者讓學生在畫出同底等高的三角形后，聚焦觀察這些三角形的聯系，從而得出等積變形的動點軌跡及面積相等的特點，并將這個規律推廣至“另外兩個頂點”。此外，筆者還引導學生通過想象推理、動手操作、還原驗證等方式，探索三角形分解變形及合并過程中整體和部分各個量之間的變與不變，深入體會圖形之間的聯系。其實質便是讓學生把握“同底等高”三角形面積相等的本質，從整體出發進行研究和思考。值得注意的是，這種結構化的整體思想還具有一定的應用價值。學生在學習“圓的面積公式”推導時，將圓分成若干個近似三角形的小扇形后，就可以從整體出發，通過等積變形將它們轉化為與之面積和相等的大三角形，進而推導出圓的面積公式。因此，我們可以預見，這樣結構化的整體思想必然會促使學生在探索學習中不斷發現新的方法、新的聯系，拓寬解決問題的思路，形成獨特的數學眼光。