Flower snark圖的書式嵌入頁數及2-頁交叉數問題

董曉媛，馬登舉

(1.南通師范高等專科學校初等教育學院，江蘇 南通 226007；2.南通大學理學院，江蘇 南通 226019)

1 預備知識

一本書是由一個書脊和k個書頁組成的，這k個書頁有一個共同的邊界就是書脊.將一個圖G嵌入書就是將G的頂點按照一定的順序放在書脊上，而把G的邊畫在書頁內，使得圖G在同一頁的邊不相交.在所有的畫法中，有一個最小的書頁數，稱之為圖G的書式嵌入頁數，記為PN(G).研究書式嵌入頁數問題的動機之一是書式嵌入在VLSI電路板設計、互聯網的容錯陣列設計等問題中的應用[1-4].圖的書式嵌入首先由Atneosen[5]提出，Kainen[6]正式給出定義.Ollmann[7]首先提出書頁數問題.把完全圖K4的所有頂點按一定的順序放到虛線上也就是書脊上，得到完全圖K4的一個書式嵌入，如圖1所示.

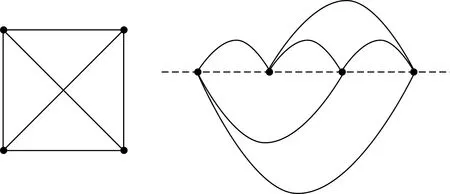
圖1 完全圖K4的書式嵌入

研究交叉數的主要目的之一是圖的交叉數在超大規模集成電路設計中的應用[8-10].一個圖的畫法滿足下列條件：(1)相鄰的2條邊不交叉；(2)2條邊相交叉不多于一次；(3)2條邊不相切；(4)沒有3條邊交于同一個頂點.在圖G的所有畫法中交叉點數最少的畫法所含的交叉點的數目稱為圖G的交叉數，記為cr(G).把圖G嵌入一個2-頁書，在這個2頁書上的所有畫法中，使得交叉點數最少的畫法所含的交叉點的數目稱為圖G的2-頁交叉數，記為cr2(G).Garey等[11]指出計算簡單圖的交叉數是NP-困難的.由于這兩個問題都是NP-困難的，所以不太容易得到通用的簡易算法.

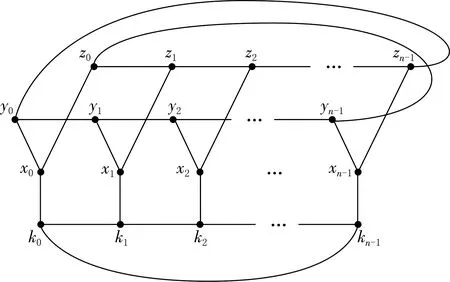
圖2 Fn的一個畫法

snark圖是源自3-邊著色猜想而構造的圖.若圖是2邊連通的3-正則圖且不可3-邊著色，同時圍長至少為5，也無非平凡3-邊割集，則稱為snark圖.廣義Petersen圖是最小的snark圖.1975年以來，更多的snark圖被發現，人們對snark圖進行了很多研究，特別是Flower snark，Goldberg snark，Blanu?a snark圖.給出Flower snark圖的定義：Gn是一個簡單的非平凡的連通的3-正則圖，點集V(G)={ki，yi，zi，xi|0≤i≤n-1}，邊集E(G)={kiki+1，yiyi+1，zizi+1，xiki，xiyi，xizi|0≤i≤n-1}，點的標號對n取模，Hn可以由Gn通過用邊yn-1z0，zn-1y0替換yn-1y0，zn-1z0得到.如果n為奇數且n≥5，Hn被稱為Flower snark圖，其他的圖被稱為Flower snark圖的相關圖，把這些圖統一用Fn來表示，見圖2.顯然，k0k1…kn-1k0為一個n圈，y0y1…yn-1z0z1…zn-1y0為一個2n圈，xi與yi，zi，ki(0≤i≤n-1)都有邊相連.

本文將給出Flower snark圖的書式嵌入頁數的簡單證明，以及Flower snark圖的2-頁交叉數結果.

2 主要結論

引理1PN(G)=1，當且僅當G為外平面圖.

引理2PN(G)≤2，當且僅當G是平面Hamilton圖的子圖.

由引理2顯然可以得到如下結論：

引理3 若G為非平面圖，則PN(G)≥3.

引理4 完全二部圖K3，3的書式嵌入頁數PN(G)=3.

2008年，Zheng等[12]研究了Flower snark圖的交叉數，由文獻[12]可得到引理5：

引理5 當n≥6時，Flower snark圖的交叉數cr(Fn)=n.

定理1 當n≥3時，Flower snark圖的書式嵌入頁數PN(Fn)=3.

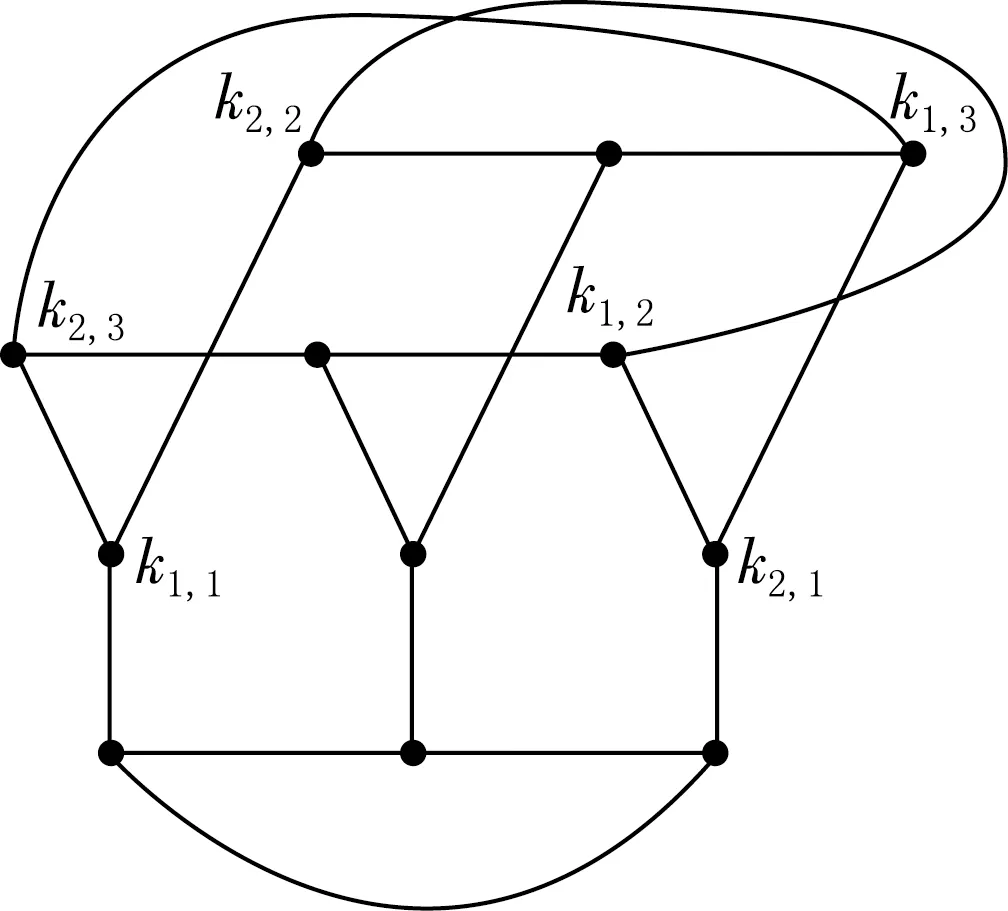
圖3 Flower snark圖中包含了同構于K3，3的子圖

證明觀察Flower snark圖，可發現Flower snark圖中包含了同構于K3，3的子圖，見圖3.

由引理4可知，K3，3的書式嵌入頁數PN(G)=3，所以Flower snark圖的書式嵌入頁數PN(Fn)≥3.

給出Flower snark圖的一個書式嵌入畫法：

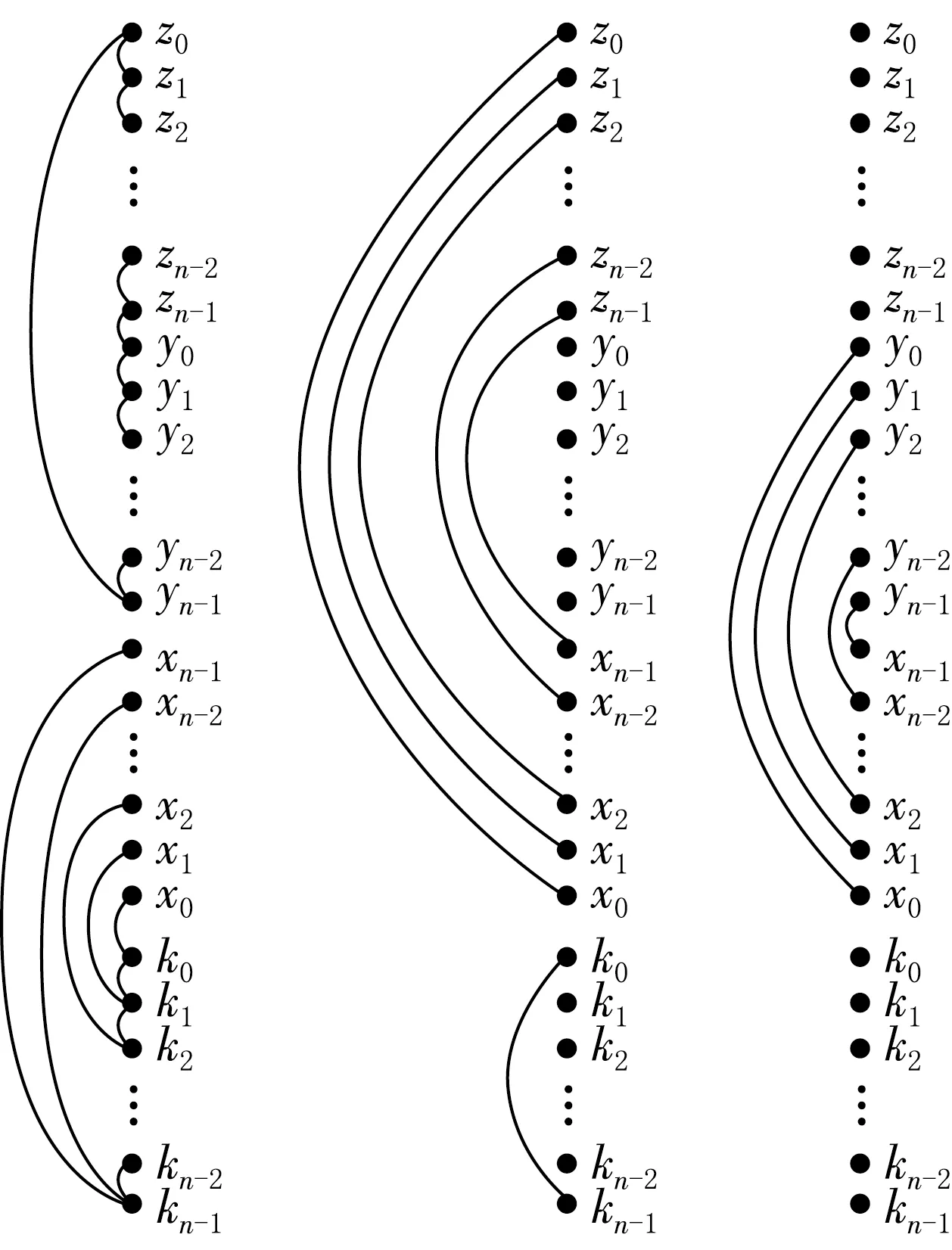
圖4 Flower snark圖的一個書式嵌入畫法

由Flower snark圖Fn的定義，它包含了點集V(G)={ki，yi，zi，xi|0≤i≤n-1}，邊集E(G)={kiki+1，yiyi+1，zizi+1，xiki，xiyi，xizi|0≤i≤n-1}.顯然，Flower snark圖中包含了一個n圈k0k1…kn-1k0，一個2n圈y0y1…yn-1z0z1…zn-1y0，并且當0≤i≤n-1時xi與yi，zi，ki都有邊相連.

在書脊上按照z0z1…zn-1y0y1…yn-1xn-1xn-2…x1x0k0k1…kn-1的順序依次排列各頂點.

第一頁：y0y1…yn-1z0z1…zn-1y0為一個2n圈，依次連接各頂點形成圈，不形成交叉點.k0k1…kn-1k0為一個n圈，先依次連接k0k1…kn-1，不形成交叉點，kn-1與k0的連線留到下一頁.又因為xi與yi，zi，ki都有邊相連，把xi與ki都相連，不產生交叉點.

第二頁：把xi與zi都相連，不產生交叉點.同時kn-1與k0相連.

第三頁：把xi與yi都相連，不產生交叉點.

由定義，把Flower snark圖的每條邊都相連了，共3頁，完成Flower snark圖的一個書式嵌入畫法，見圖4.

從給出的畫法可以看出PN(Fn)≤3.

綜上，當n≥3時，Flower snark圖的書式嵌入頁數PN(Fn)=3.

定理2 當n≥6時，Flower snark圖的2-頁交叉數cr2(Fn)=n.

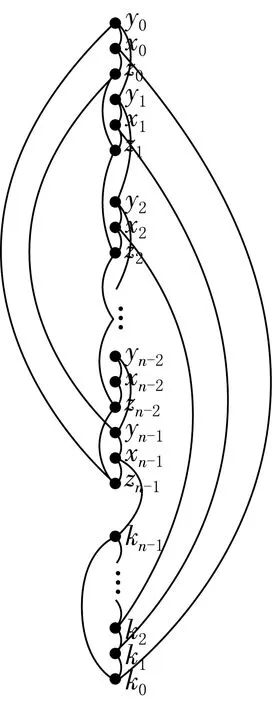
圖5 Flower snark圖的一個2-頁書畫法

證明由引理5可知，當n≥6時，cr(Fn)=n.又因為cr2(Fn)≥cr(Fn).這樣得到了當n≥6時，cr2(Fn)的下界，即cr2(Fn)≥n.

由Flower snark圖Fn的定義可知它包含了一個n圈k0k1…kn-1k0，一個2n圈y0y1…yn-1z0z1…zn-1y0.并且當0≤i≤n-1時xi與yi，zi，ki都有邊相連.由2-頁書畫法的定義可知，把一個圖嵌入到這本書中，這個圖的每個頂點都位于書脊上，每條邊都位于同一頁上.

在書脊上按照y0x0z0y1x1z1y2x2z2…yn-1xn-1zn-1kn-1kn-2…k1k0的順序依次排列各頂點.首先，k0k1…kn-1k0為一個n圈，依次連接各點，不產生交叉點.y0y1…yn-1z0z1…zn-1y0為一個2n圈，依次連接各點，邊zn-2zn-1與yn-1z0相交共產生1個交叉點.其次，xi分別與yi，zi相連，不產生交叉點.最后，xi與ki相連，當0≤i≤n-2時，每條邊xiki都與yiyi+1產生一個交叉點，共n-1個交叉點.當i=n-1時，每條邊xn-1kn-1不與其他邊產生交叉點.綜上，共產生n個交叉點.

因此得到一個Flower snark圖的2-頁畫法，并發現共產生了n個交叉點，見圖5.從而得到cr2(Fn)的一個上界：當n≥6時，cr2(Fn)≤n.

綜上，當n≥6時，Flower snark圖的2-頁交叉數，cr2(Fn)=n.