一種基于稀疏搜索的激活噪聲快速聚類算法
郭林亮,韓旭明,張逸航
(1.長春工業大學數學與統計學院,吉林 長春 130012;2.暨南大學信息科學與技術學院,廣東 廣州 510632;3.長春工業大學計算機科學與工程學院,吉林 長春 130012)
0 引言
聚類分析是無監督學習中的重要方法.在樣本沒有給定類別信息的情況下,聚類分析根據計算樣本特征的相似性來確定樣本的分組,同一分組的樣本具有高度的相似性,而來自不同分組的樣本之間相異度高[1].聚類算法可以以無監督的方式找到數據的特征分布結構,所以研究者們提出了很多不同類型的聚類算法,并被廣泛應用于以空間信息處理為代表的眾多領域[2],例如,圖像分割、模式識別等[3-6].
大多數現有的聚類算法在處理局部和非線性數據模式方面都有很大的局限性[7].針對形狀復雜、噪聲比較多的數據集,這些聚類算法沒有很好地解決參數多且不易調節的問題,且對噪聲和緊鄰類之間的連接點的分配也不合理.
實現聚類的眾多方法中,基于密度的聚類方法是比較流行且高效的.文獻[8]利用密度可達的方式去鏈接eps鄰域獲得子簇;在此基礎上,研究者們提出了許多變體算法來獲得更好的聚類性能[9];文獻[10]提出了一種快速的近似KNN的算法來判斷和確定核心塊、非核心塊和噪聲塊;文獻[11](DPC)選取乘積較大的幾個點作為聚類中心,從而確定類的個數;文獻[12](FSDPC)設計了一種新的稀疏搜索策略來衡量每個數據點的最近鄰居之間的相似性;文獻[13]設計了一種數據點關聯度轉移方法和分層方法來選擇聚類中心;文獻[14](DPC-DBFN)使用基于k近鄰的模糊核密度對決策圖進行分區來確定類的個數,同時分配邊界區域和噪聲;文獻[15]提出在一定半徑鄰域尋找最大密度點,并把它們作為聚類中心,避免了選擇聚類中心個數的問題;文獻[16]采用覆蓋樹的方法快速計算數據點密度;文獻[17]采用了樹的結構獲得初始的子類,再計算這些子類的相似度來進行層次聚類;文獻[18]先采用近鄰的方式獲得基本的簇,再通過圖的方式進一步分割這些簇;文獻[19]以共享近鄰的方式確定數據點的密度,并選擇密度最大的幾個數據點作為代表點進行層次聚類得出最后的聚類結果.
以上的聚類算法取得了一定的成就,但還存在以下不足:算法雖然減少了運行時間成本,但卻降低了邊界點和噪聲分配的效率;在處理彼此靠近類的連接處的點時,由于預設的參數較多,引起連鎖反應導致噪聲點沒有有效分配,使聚類結果出現偏差.
為了解決這些問題,本文提出了一種基于稀疏搜索的激活噪聲快速聚類算法(ANSC).本文算法利用數據總體離散度與個體近鄰屬性的關系重構密度函數,把分布結構復雜的數據點映射到簡單的自定義密度函數上,通過觀察密度函數的性質來激活潛在的噪聲.按照有規律的步長規則快速尋找稀疏互連點,并以粗化和細化分割數據點的方式共建這些互連點形成子類,利用子類間距離的分布特性來合并.在獲得初步的聚類結果后,根據噪聲的分布特點判斷是否形成新的目標類.因此,對于不同形狀的數據集,針對如何處理噪聲、減少參數的數量和降低時間成本的問題,本文提出了ANSC.
1 ANSC
1.1 激活噪聲
提出的算法使用近鄰的方式確定數據點的密度,這種方式可以反映數據的總體離散度和個體近鄰之間的關系.當一個數據點與周圍點的距離和標準差較大時,它的密度會很小,甚至小于0.這種方式可以把分布結構復雜的數據點映射到密度函數上,通過觀察函數的性質挖掘潛在的噪聲.與神經網絡中設置的激活函數的意義類似,認為在密度小于0的數據點是不需要被關注的點,并把這些點定義為噪聲,實現激活的作用.
為了減少重復的距離計算,算法采用快速k近鄰的方法(如kd-tree[20]),僅通過搜索近鄰以減少數據點間距離的計算次數.此過程只設計一個易于調節的近鄰參數k.這種設置方式減少了聚類過程中參數的數量.
假設數據集為X={x1,x2,…,xn},其中n是數據點的個數.數據點xi與所有近鄰距離的和Dis(xi)=sum(knn_dist(xi,:)),其中knn_dist(xi,:)代表數據點xi的近鄰距離的集合.定義Dis={Dis(x1),Dis(x2),…,Dis(xn)}.
借助數據近鄰和標準差與離散度的關系,定義了總體離散度Gdis的概念,定義為
(1)
其中:d是數據的維度,mean表示求數據的均值,max表示求數據的最大值,st是所有st(xi)的集合,st(xi)代表數據點xi與所有近鄰點的標準差.
為了體現數據個體與總體的離散關系,有效地確定噪聲,定義了數據點的密度函數為
(2)
從公式(2)可知,隨著總體離散度的增加,數據個體的密度在逐漸減小,當密度小于0的時候,則認定數據點為噪聲.如果一個數據集中密度小于0的點比較多,則數據集中的噪聲也很多,能夠反應這個數據集的數據分布比較松散,為后續的識別和判斷噪聲的類別提供了基本的保障.在實驗中可以改變近鄰的個數來實現數據點密度的變化,從而確定不同的噪聲點和類連接處的點.
1.2 近鄰互連共建子類
與現有的構建子類的方法不同,本文以步長的方式稀疏搜索數據確定互連點,再以先粗化后細化的分割方法共建這些點形成子類.按照類與類的性質,相似性大且距離比較近的點屬于一個類的幾率更大.
基于以上想法,本文提出在一個隨機數據點的最大近鄰索引的基礎上,設置一個步長去尋找下一個數據點的方法.同時,定義以這種方式尋找到的數據點為互連點.如果互連點間滿足一定的閾值條件,就鏈接這些互連點形成子類,這個過程叫作粗化共建.在此基礎上,為了進一步分裂彼此靠近的類,需要細化共建這些互連點.選擇每個子類中密度最大的點為代表點,代表子類,并把這些代表點稱為共建點.
假定搜索到的互連點個數為n1,所有的數據點都是未訪問點.
粗化共建:找到第一個未訪問的互連點xi及它的近鄰,在此基礎上,不斷尋找其他互連點.若兩個數據點索引之間滿足以下條件,則停止粗化共建,并標記這些互連點為已訪問:
Index(xi)-Index(xc) (3) 此時xc是當前需要判斷類別的數據點,Index(xi)代表數據點xi的索引. 細化共建:在粗化共建的基礎上,尋找未訪問的第一個互連點.若數據點索引之間滿足以下條件,則進行細化共建,并標記這些互連點為已訪問: (4) 其中:knnj(xi)表示離xi最近的第j個點,Round表示向上取整函數. 由共建點的定義可知,共建點是子類中密度最大的點.如果兩個共建點之間的距離小于共建點間的最小距離均值時,就認為它們代表的子類應該屬于一個類,所以需要合并一些相似度大的子類.這種合并的方式與層次聚類相似,但是實現途徑是不同的.本文算法中類的個數可以根據共建點的分布特點自動地確定,無須的人為的干預.對于所有的剩余點,未訪問的點歸類于最近的類. 為了減少噪聲對聚類結果的影響,提出兩種分配噪聲的方法:一是連續出現噪聲的個數n3;二是噪聲與它的近鄰之間的關系.如果連續出現很多噪聲,則認為這些噪聲可以構成一個新的類,并把它們定義為近類噪聲.如果當前噪聲與近鄰所屬的類距離比較遠,把這些點形成一個新的類,并定義它們為遠類噪聲. 假定當前的聚類結果中有n2個子類,每個子類中數據點的個數分別是{num1,num2,…,numn2}. 近類噪聲:存在連續的噪聲,且它們的個數和為n3,如果滿足以下條件: n3>(num1+num2+…+numn2)/n2. (5) 遠類噪聲:假定噪聲為點noi,它與最近鄰點knn1(noi)的距離為Ndis,它的第k個近鄰為knnk(noi),Kdis是knnk(noi)所有近鄰距離的平均值,滿足以下條件: Ndis>n2*Kdis. (6) 本文提出的算法由以上3個模塊組成,描述如下: 第1步:按照公式(2)獲取每個數據點的密度,根據密度的大小來確定噪聲點; 第2步:隨機選擇一個初始點,如果初始點的最大近鄰不是噪聲點,則把最大近鄰點認為是第一個互連點,在此互連點的基礎上以4*k的步長尋找下一個初始點;否則以2*k的步長尋找下一個初始點,直到所有的數據點都被搜索結束; 第3步:通過第2步可以獲得很多個互連點,把所有的互連點組成一個新的數據集,在此基礎上獲得共建點,再按照公式(3)和(4)定義的方式獲得粗化共建和細化共建的子類; 第4步:就近分配未訪問點,按照公式(5)和(6)的原則去分配近類噪聲或者遠類噪聲; 第5步:得到最后的聚類結果. 本文計算數據點密度的時間復雜度是O(nlogn).在近鄰互連共建子簇、合并子簇和分配剩余數據點的過程中,只計算互連點之間的距離,而互連點的個數遠小于數據個數,所以這部分的時間復雜度不高于O(n).綜上所述,ANSC的算法的時間復雜度為O(nlogn),小于對比算法的時間復雜度O(n2). 為了驗證ANSC算法的有效性,使用最新聚類研究中經常使用的10個人工和真實數據集進行實驗.ANSC與最新的聚類算法進行了比較,包括算法FSDPC[12]、DPC-DBFN[14].為了排除對比算法在改變參數時對聚類結果的影響,在實驗過程中采取多次微調參數的方式,并選用最好的評價指標作為聚類結果.所有算法的實驗都是在MATLAB 2018 a環境上實現的.所有數據集的信息如表1所示,它們都來自UCI 數據庫. 表1 全部數據集 為了進一步比較3種聚類算法在10種數據集上的聚類方法可靠性和性能,本文使用3種常見的外部聚類評價指標,包括準確度(ACC)、歸一化互信息(NMI)[21]、調整蘭德系數(ARI)[22].若這些指標的值越大越好,越接近1,則表示聚類算法的實際效果越好.在人工和真實數據集上的實驗結果如表2所示. 表2 3種算法在3個評價指標上的結果 在實驗中,算法采用的聚類準確度評價指標ACC定義為 根據表2的實驗結果可知,在解決不同形狀的人工和真實數據集時,所提出的算法都是可行的,提高了聚類算法的性能指標,并且3個性能評價指標都是最高的.對于對比算法,算法DPC-DBFN的聚類效果在解決非凸數據集時,效果是最差的;算法 FSDPC比DPC-DBFN展示了更好的聚類結果,但是在解決密度不均勻的數據集時,兩個算法的聚類結果表現都一般. 通過以上實驗結果的分析,所提出的ANSC對非凸數據的邊界和類連接處點的處理方式是有效的;從3個聚類的評價指標可知,相對于2個較新的對比算法,本文算法對非凸數據集是有效且高效率的聚類. 本文針對聚類算法中對噪聲和邊界分配不合理的問題,提出了一種基于近鄰互連共建的ANSC.此算法包括3個核心部分:激活潛在的噪聲;以步長的方式快速搜索互連點來達到共建子簇;判斷噪聲類型.本文算法利用數據總體離散度與個體近鄰屬性的離散關系重構具有代表性的密度函數來獲得噪聲;通過快速確定近鄰互連點來獲得新的共建數據點;通過噪聲的分布特點來優化其類別. 與較新的聚類算法相比,在10個人工和真實數據集上的實驗結果表明,本文提出的方法在噪聲和類連接處點的合理分配問題上是有效的和可靠的.在預設參數少和運算時間成本低的情況下,提高了聚類算法的效率和性能.1.3 識別和檢測噪聲
1.4 時間復雜度分析
2 實驗結果
2.1 實驗對比
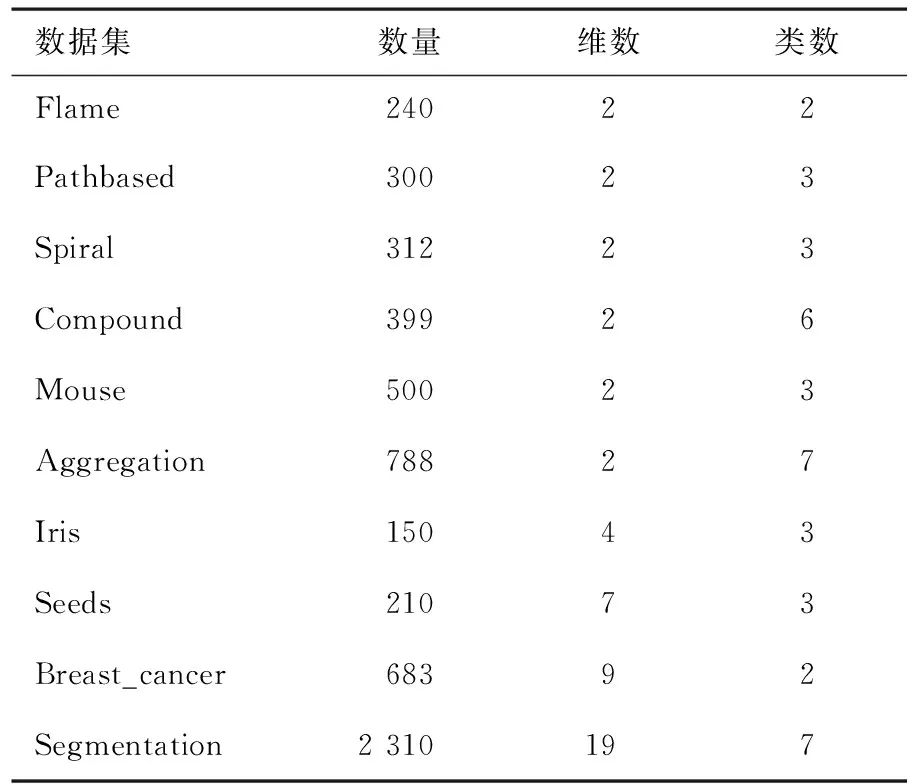
2.2 性能評估
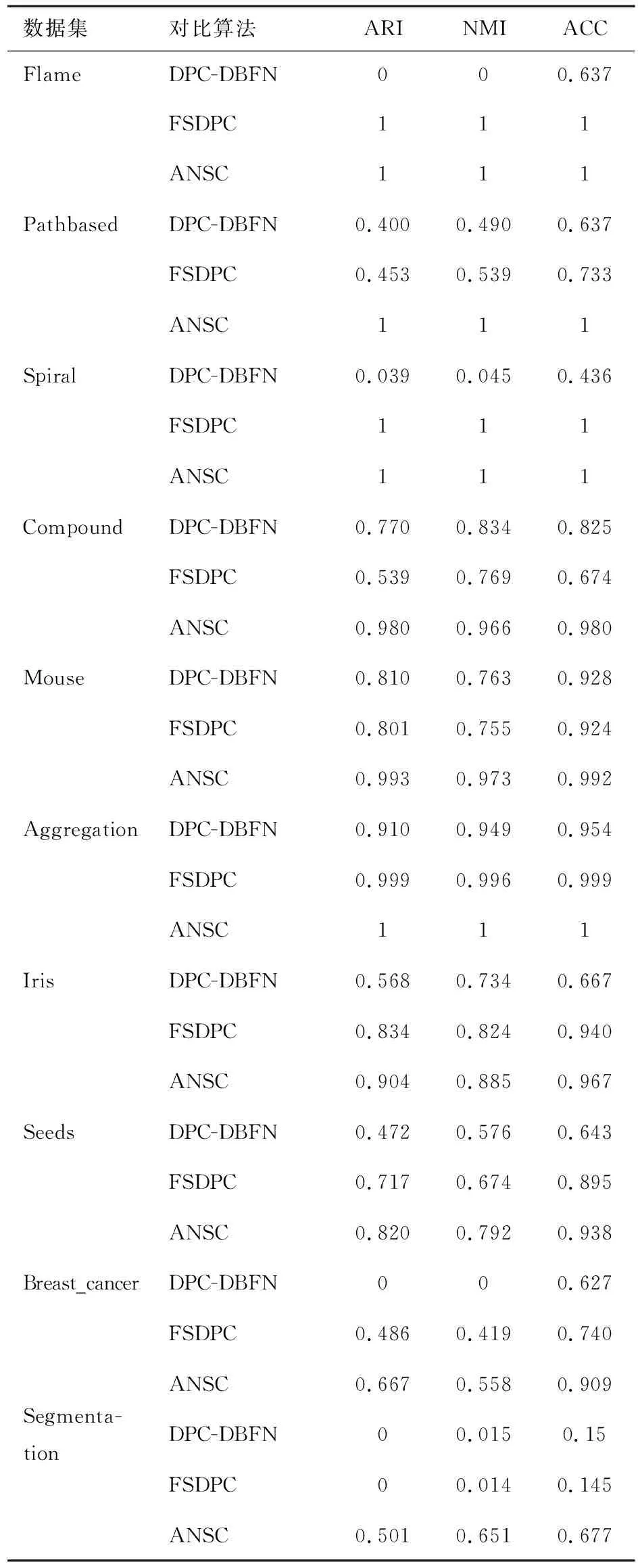
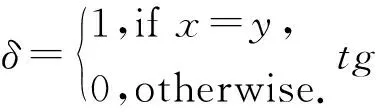
2.3 結果與分析
3 結論

