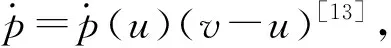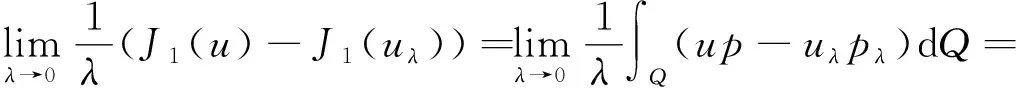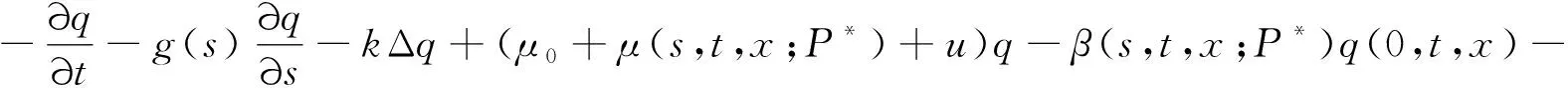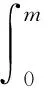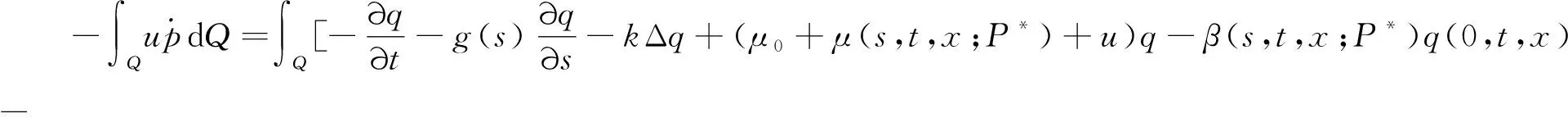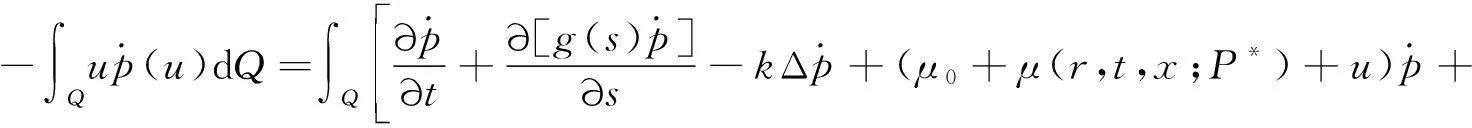周期環境下尺度結構隨機種群擴散系統的最優收獲
卜 紅 彧
(遼東學院師范學院數學系,遼寧 丹東 118003)
1 問題的提出
在種群問題的研究過程中,考慮到種群擁擠和生存環境限制對種群發展過程的影響,相應的數學模型關于狀態函數就是非線性的.文獻[1]研究了年齡和時滯的非擴散種群系統的最優生育率控制;文獻[2]研究了年齡結構和加權的隨機種群系統的最優邊界控制;文獻[3]研究了一類污染環境下具有擴散和年齡結構的隨機種群系統強解的存在唯一性;文獻[4]研究了一類非隨機周期種群系統的最優收獲;文獻[5]研究了尺度結構的非擴散隨機種群系統的最優輸入率控制;文獻[6-8]研究了個體尺度結構下競爭種群系統的最優收獲控制、最優邊界控制和最優輸入率控制;文獻[9]研究了非隨機種群擴散系統的最優收獲條件.在上述基礎上,基于周期環境,只有考慮到種群的尺度結構、擴散系數和隨機因素的影響,才更加符合種群生存的實際.本文討論如下具有尺度結構的隨機種群擴散系統(P):
(1)
在上述模型中:固定常數m,T分別表示種群個體最大尺度和系統演變周期,0
(2)
討論下面的最優收獲控制問題:尋找u∈U,使得
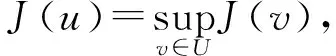
(3)
其中容許控制集為
U={v∈L∞(Q)|0≤v(s,t,x)=v(s,t+T,x)≤L<+∞,a.e.于Q內}.
2 基本假設
本文假設如下條件成立,其中Mi(i=1,2,…,6)為常數:
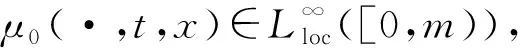
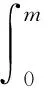
(H2)μ(s,t,x;y)與β(s,t,x;y)關于y二次連續可微,且
0≤μ(s,t,x;y),β(s,t,x;y),|μy(s,t,x;y)|,|βy(s,t,x;y)|≤M2a.e.于Q×+上,
μ(s,t+T,x;P(t+T,x))=μ(s,t,x;P(t,x)),β(s,t+T,x;P(t+T,x))=β(s,t,x;P(t,x));
(H3) 0≤p0(s,x)≤M3<+∞ a.e.于Ωm內,滿足相容性條件:
(H4)g(s)是(0,m)上連續可微增函數,0 (H5) 連續函數g′(s,t,x)滿足g′(s,t,x)=g′(s,t+T,x); (H6) 0≤k(s,t,x)≤M6<+∞于Q內. 按照文獻[10]引進一些記號:設H1(Ω)是Ω上的一階Sobolev空間,即 V=L2(0,T;H1(Ω))是定義在[0,T]上取值在H1(Ω)中的Hilbert空間.V′為V的對偶空間L2(0,T;(H1(Ω))′). 定理2[4]設(H1)—(H6)成立,則問題(3)在U中至少存在一個最優控制u∈U. (4) 其中: uλ=u+λ(v-u),0<λ<1;pλ=p(uλ);p=p(u). (5) 由(4)和(5)式有 (6) (7) (6)與(7)式作差,將所得方程兩端除以λ>0,令λ→0+易得 (8) 定理3 設u∈U是問題(3)的最優收獲控制,則u∈U滿足 (9) 證明由性能指標泛函J(v)的結構式(2)和u∈U為最優收獲控制及(5)式,對0<λ<1得 為了變換(9)式,定義如下的共軛系統: (10) q(s,t,x)=q(s,t+T,x),在Q內; (11) q(m,t,x)=0,在ΩT內; (12) q(s,T,x)=0,在Ωm內; (13) q(s,t,x)=0,在∑上; (14) (15) 上式等號右邊關于變量s和t分部積分,并注意到(8)和 (11)—(15)式,得 所以有與(9)式等價的變分不等式: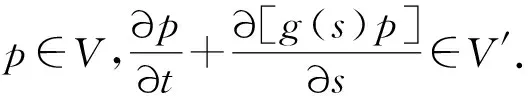
3 最優收獲條件