基于學科核心素養的高中數學新舊教材習題的比較研究
——以解三角形為例

沈小雪 宋玉軍

（佳木斯大學理學院 黑龍江佳木斯154000）

自2017版高中數學課標頒布以來，各省分批開始新一輪的課程改革。隨著課改的不斷深入，教材也隨之發生改變。現在，我國高中普遍使用的數學教材共有5版，分別為人教A版、人教B版、北師大版、湘教版、蘇教版，從而使我國形成一綱多版的局面。面對新課改提出的要求，人教A 版在解三角形部分進行了很大改變。在高中的數學知識體系中，解三角形具有重要地位，并且它也是高考常見題型之一。而習題部分，課前作為預習，能夠了解本節要學習的內容；課上作為練習，能夠鞏固知識的學習；課后作為知識點的補充，能夠檢測學生的學習效果。因此，習題在一章當中成為不可或缺的一部分。綜上，分析解三角形部分的習題是很有必要的。

1 基于數學學科核心素養的比較分析

對新舊教材的習題進行統計時，按照以下標準進行統計：教材中，以1、2、3……編號為大題，以（1）、（2）、（3）……編號為小題，凡是大題中有小題出現時，皆按小題數量計算。另外，統計的習題包含每節標有“練習”“習題”和“復習參考題”字樣的部分。依據以上標準，按照各題目所體現的數學核心素養進行統計，如表1和表2所示。

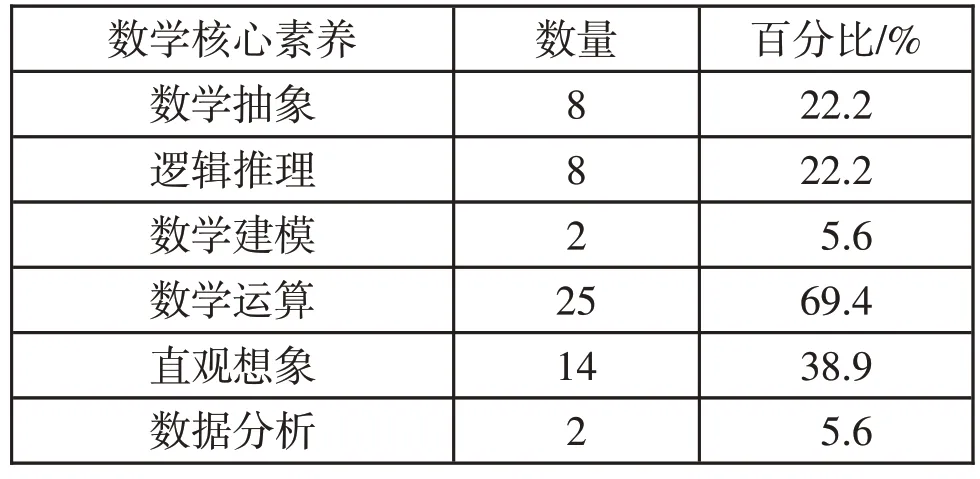
表1 新教材各題目所體現的數學核心素養比較

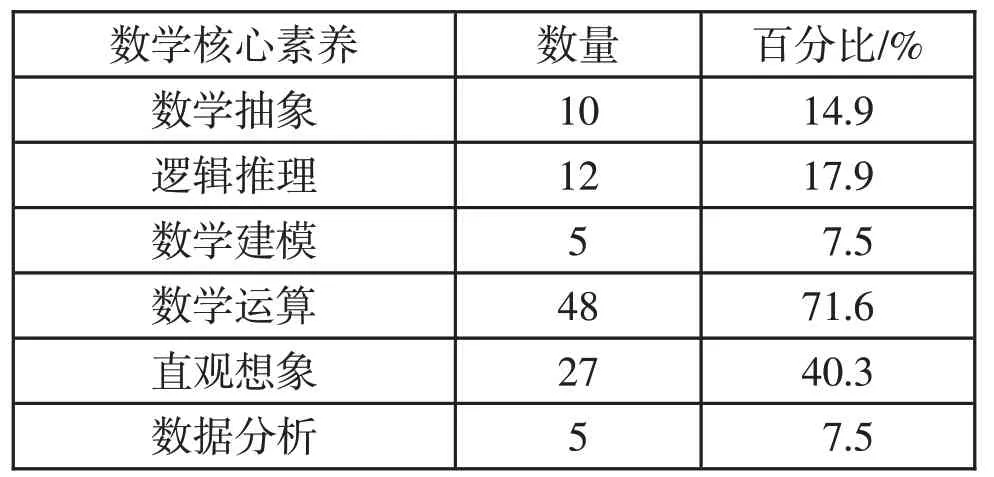
表2 舊教材各題目所體現的數學核心素養比較

1.1 數學抽象維度的比較分析

數學抽象是指通過對數量之間的關系，或是空間形式上的變化的抽象，進而得到數學研究對象的素養。新教材中體現數學抽象素養的題目共有8 道，占總量的22.2%；舊教材中則有10道，占總量的14.9%。相較于舊教材來說，新教材在這方面的占比略高。由此可見，這次的教材編寫注重培養學生的這一素養。

例如，新教材中習題6.4 的“你能用三角形的邊和角的正弦表示三角形的面積嗎？”這一道題，在舊教材中，與它類似的題目是這樣描述的：“就三角形的面積計算問題作一探索，你現在已經學習了哪些計算公式，還可發現和證明一些新的計算公式嗎？”

這兩道題的立意都是希望學生能夠通過對正弦定理的學習，自主探索總結出三角形的面積公式。新教材在題目中直接給出推導的思路，而舊教材沒有。相比之下，新教材題目的表達更加符合學生的發展認知，更加有利于學生獲得數學的某種規則，培養數學思維，形成數學體系［1-3］。

1.2 邏輯推理維度的比較分析

邏輯推理是學生學習數學應具備的基本能力之一，它是指根據已知判斷推出新判斷的一種能力。借助邏輯推理能力的培養，使學生建構數學知識體系，且能夠找到錯綜復雜的事物之間的本質聯系。新教材中，凸顯邏輯推理素養的題目基本是延續了舊教材，但是新教材的題數占總數的22.2%，而舊教材為17.9%，新教材高于舊教材4.3%。由此可見，在對學生邏輯推理能力的培養上，新教材比舊教材更加重視。

1.3 數學建模維度的比較分析

數學建模是指將實際問題抽象為數學問題，再運用數學知識和方法對問題進行設計和實施，從而建立數學模型解決問題的素養。在新教材中，體現數學建模素養的題目數量僅占總數的5.6%，而舊教材為7.5%，新教材比舊教材低了1.9%，可見數學建模這一核心素養在新教材的體現度略低。數學建模是連接實際生活與數學知識的一道橋梁，是數學在應用方面最好的體現，也是以后學習高等數學必備的數學思想。在高中階段學會數學模型，一方面，可以培養學生發現、分析、解決問題的能力，增強用數學語言表示實際生活的感覺；另一方面，可以認識數學模型在生活中的多種作用，提升學生的動手操作能力，增強創新意識。因此，新教材應該適當增加數學建模方面的習題［4-6］。

1.4 數學運算維度的比較分析

數學運算是指明確計算目標，根據適當的運算法則解決數學問題。主要包括：定對象，懂法則，理思路，求結果。從表1和表2中可以看出，新教材對體現數學運算素養的這類題目進行了刪減。對于這種純運算直接應用定理，只能機械強化學生思維的題目，與“全面發展”這一教育理念背道而馳，因此，新教材在修訂時特別注重多種素質的共同培養。

1.5 直觀想象維度的比較分析

直觀想象是指通過借助幾何直觀和空間想象認識事物的變化過程，利用圖形加深理解，從而解決數學問題。主要包括：通過空間形態認識事物；利用圖形分析問題等。通過表1和表2發現，新教材習題體現直觀想象素養的數量占總體38.9%，而舊教材為40.3%，二者相差不大，從占比來看，直觀想象這一核心素養均是新舊兩版教材中解三角形部分主要體現的核心素養之一，在高中數學學習中直接展現這一素養的典型思想就是數形結合。借助這類題目的練習，可以幫助學生在解題過程中建立數形結合的思想，提升空間想象的能力。

1.6 數據分析維度的比較分析

數據分析主要指具備對數據處理、分析的敏感度，能夠真實且有用地獲取數據信息，并且對于數據結果進行合理、科學的統計，從而在數據分析的過程當中獲得有價值的信息內容，進而實現對于數據的利用。通過在高中階段的學習，使學生能夠提高獲取信息、處理信息和應用信息的能力及意識，增強運用數據表達現實問題的能力，以此讓學生逐漸具備用數據印證事實的思維。從表1 和表2 中可以看出，在這部分習題中，體現數據分析素養的題目和體現數學建模素養的題目是直接掛鉤的。因此，新教材在這個素養上是低于舊教材的，但是差距并不是十分明顯，教師在對這類題目進行講解時應融入其他與之類似的題目。

2 習題難度的比較研究

2.1 習題數量比較

依據以上標準，對新舊教材解三角形部分習題的統計數量，如表3和表4所示。

表3 新教材習題數量分布表

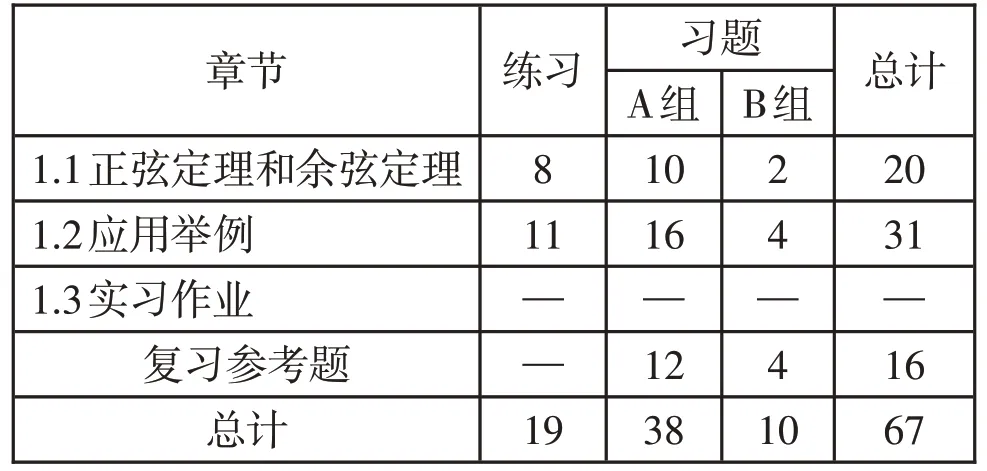
表4 舊教材習題數量分布表

從數據結果看，新教材的習題總數為36 道，舊教材的習題總數為67道，新教材的數量比舊教材少了近一半。造成這一現象的主要原因是編排方式的改變，在舊教材中解三角形獨成一章，共有三小節，由于第三節是實習作業，所以沒有對應的習題，前兩節都有練習和習題部分，在章節的最后還有復習參考題。而在新教材中，解三角形僅僅是作為平面向量的應用出現，只占了一節中的一部分，除了有單獨的練習外，并沒有與之配套的習題和復習參考題。

在這部分中，還有一個最顯著的變化，新教材中題目所給出的三角形元素突出“特殊角”的作用。與舊教材相比，新教材題目中所給出條件不會過于復雜，說明它更加注重定理的應用。在應用舉例部分，新教材數量明顯比舊教材少很多，但并不是說新教材不重視定理在實際生活中的應用。這樣設計的原因有二：一是在前面提到編排方式上的改變；二是舊教材中此部分的習題數量對于學生而言過于繁重，由于學生剛剛學完解三角形的知識，認知正在處于建構階段，而應用舉例的習題通常題干過長，難以理解，若這部分題目過多，易使學生在錯誤中感到沮喪，進而失去解題的興趣。

2.2 習題綜合難度分析

根據鮑建生的綜合難度模型，選取新教材的36個題目和舊教材的67 個題目為研究對象，從習題的背景、探究、運算、推理、知識5個因素進行分析。下面結合解三角形這部分習題的特點對5個因素的每個水平進行闡述，如表5所示。

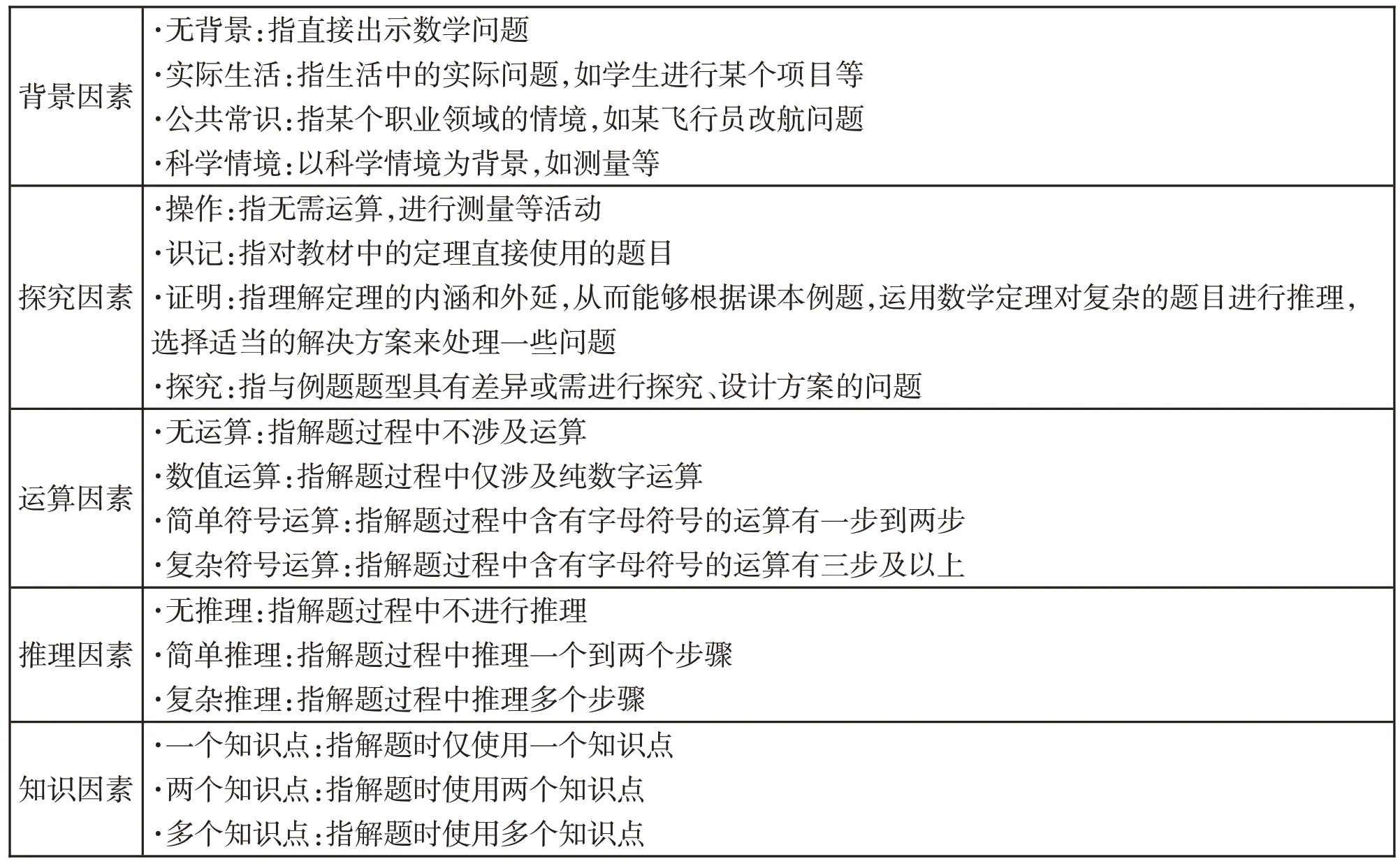
表5 習題難度各因素水平描述

根據以上界定，通過對兩本教材解三角形部分的習題的比較，它們的難度統計如表6所示。

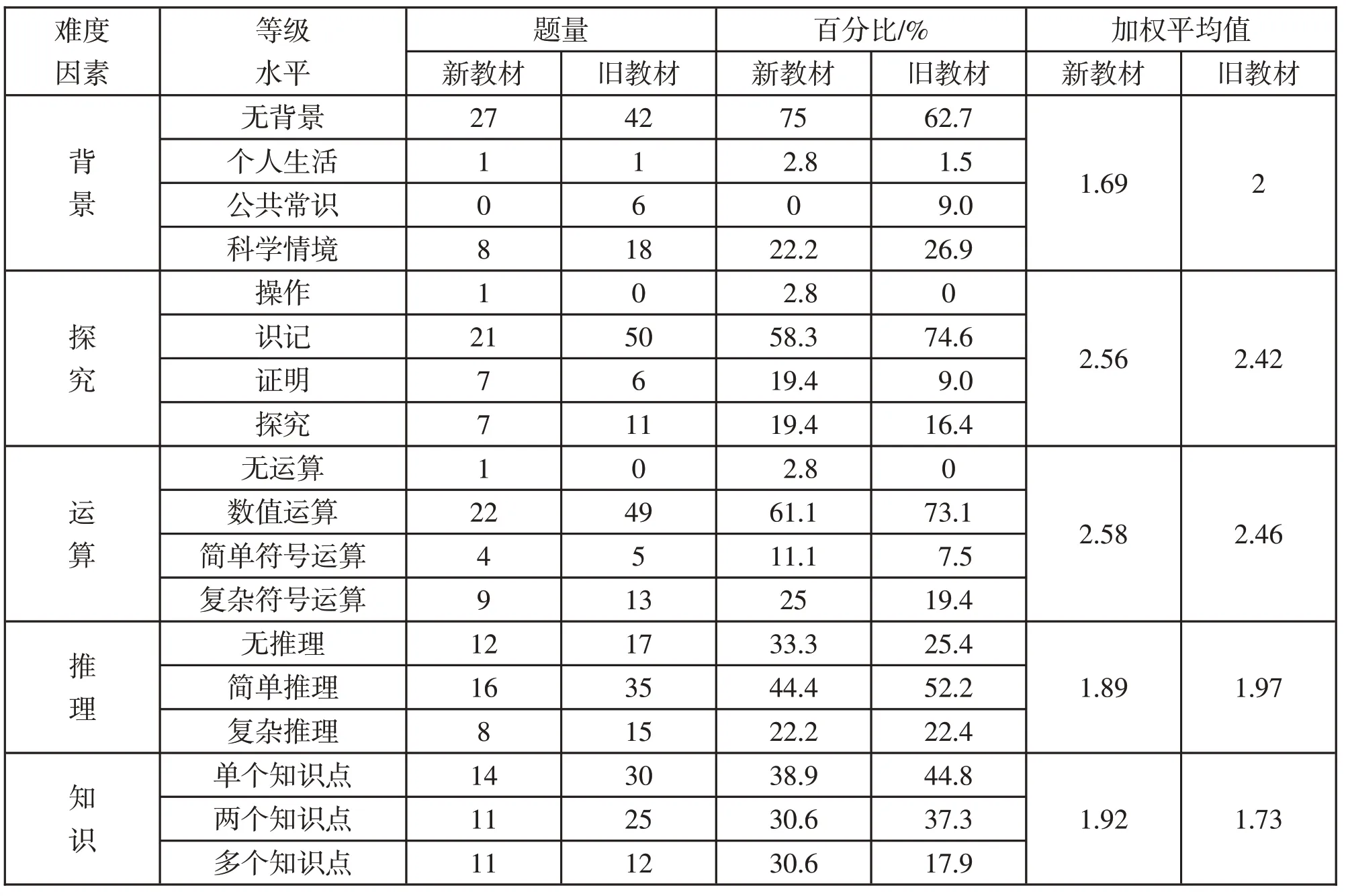
表6 新舊教材解三角形部分習題難度比較

通過觀察圖1分析，不管是新教材還是舊教材，習題的運算部分都是要比其他部分的難度略大一些，分別為2.58 和2.46，可見新舊教材在解三角形部分更加注重對定理的理解以及定理在數學運算上的應用。另外，兩本教材的主要不同之處呈現在背景和知識兩個方面。從背景方面來看，新教材的難度值小于舊教材，造成這一結果的主要原因是新教材在章節分布上的變化。在新教材中，解三角形被安排在了平面向量這一章，作為平面向量的應用出現，其中，這節還有平面向量在物理中的應用，這部分的增加使得解三角形中帶有背景的題目減少。從知識方面看，新教材的難度值高于舊教材，說明這本教材在編寫上對知識內容做出了新的要求。高考數學通常是將解三角形的知識與其他知識交匯考察，為適應高考，新教材在進行編寫時應注重多種知識的融會貫通。

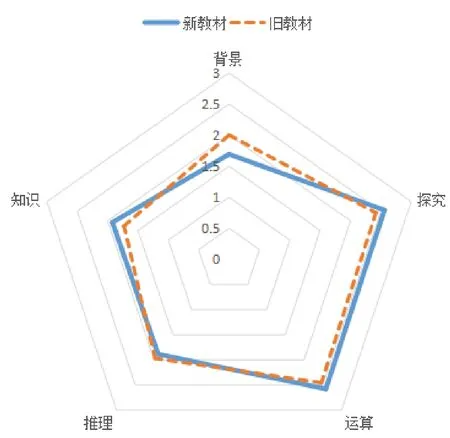
圖1 習題難度雷達圖

3 結語

通過對新舊教材解三角形部分的習題的難度和基于核心素養分析習題兩個維度進行研究，新教材的習題更加注重學生的數學抽象、邏輯推理的能力。此次改編充分考慮到學生的知識建構能力，重視各核心素養在學生身上的結合作用，在學生穩步前進的同時，更加關注他們的全面發展，落實了“立德樹人”的根本任務。