基于模糊熵與CS-ELM的供輸彈系統早期故障識別

韓慧苗，許昕，潘宏俠,2，李磊磊

(1.中北大學機械工程學院，山西太原 030051；2.中北大學系統辨識與診斷技術研究所，山西太原 030051)

0 前言

供輸彈系統是非常復雜的機電液一體化系統，作為火炮等某些高速自動武器中重要的一部分，由于它運動時猛烈撞擊等現象頻發，該系統工作的可靠性成為故障診斷領域專家研究的重點。若在系統故障發生之初就可知并給予維修和保養就能減少很多損失。因此，尋找一種能夠提高供輸彈系統早期故障診斷率的方法具有重要意義。

熵用于度量時間序列的復雜程度，在供輸彈系統的故障識別應用中，付志敏通過提取近似熵和樣本熵對它進行識別。樣本熵雖然精度比近似熵更高，但是有無法對信號在不同尺度上的復雜程度進行充分表征等問題，然而模糊熵不僅能通過不同時間序列的子序列之間對應位置元素的最大差值表征它們之間的距離，也可表征時間序列的幅值；梁振奇通過建立基于模糊熵的路段評價模型對城市路段交通狀態進行評價;丁偉等人通過提取模糊熵作為齒輪故障的特征值對各種故障狀態進行分類,他們均取得了較好的效果。相比于其他的信息熵，模糊熵能較好地表征時間序列之間的差別，所以本文作者引入模糊熵特征指標表征供輸彈系統的早期故障特征。

極限學習機(Extreme Learning Machine,ELM)算法是由黃廣斌教授等提出的，該算法在應用中表現出很強的優勢，當下已被運用到很多回歸和分類問題中，但是由于隱層節點數往往為手動輸入，導致預測結果的準確率較低。學者們提出許多優化算法來解決此問題，GENG等運用FAPH對ELM算法進行改進，YANG等也對ELM算法進行過改良，但是他們都未對極限學習機的模型結構進行改進，而且還存在構建模型復雜和計算量大的問題。布谷鳥搜索(Cuckoo Search，CS)算法除所需參數少之外，搜索目標的路徑選擇也比較優秀，整體的尋優能力強、效率高。因此，本文作者采用CS算法對極限學習機模型進行優化改進。

本文作者將模糊熵能量特征提取與CS-ELM運用于供輸彈系統早期故障預示中。經試驗驗證，該方法能有效識別供輸彈系統的早期故障，準確率達90.7%。

1 自適應TQWT濾波器算法

可調品質因子小波變換(Tunable Q-factor Wavelet Transform，TQWT)理論是由SELESNICK提出的。在TQWT中，=(,,)影響著可調品質因子小波和需要處理的時間序列特征分量的相似性匹配，其中為參數品質因子、為過完備系數、為分解的層數，對、、的選擇在故障特征提取與降噪中相當重要。針對參數空間下特定的(,,)，基于能量加權歸一化小波熵INE(,,)的可調因子小波變換的具體過程為：

(1)對二維參數網格空間(,)進行定義：

{(,)|∈[∶∶],∈[∶∶]}

(1)

其中:{∈[∶∶]}是的取值范圍和增量；{∈[∶∶]}是的取值范圍和增量。

(2)對參數組合(,)選取合理的,若和確定，則的計算公式如下：

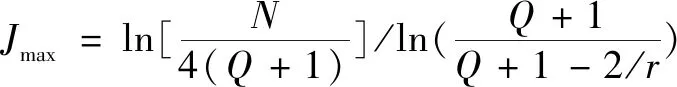
(2)

其中:是所輸入的時間序列()的長度。則較為合理的分解層數=min(,)

(3)針對可調因子小波變換=(,,)構成的參數空間，對輸入時間序列()進行多尺度可調因子小波變換分解：

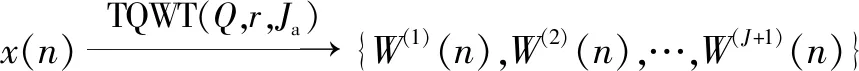
(3)

(4)用(,,)來評估TQWT多尺度分解小波系數的稀疏性。 當可調因子小波變換的參數組合為(,,)時，通過以下3個公式計算INE(,,)：

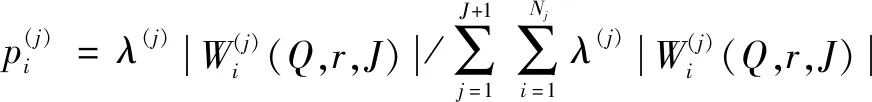
(4)

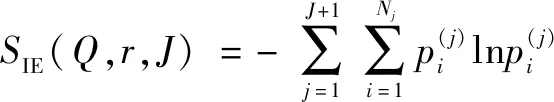
(5)

INE(,,)=(,,)max{IE(,,)}

(6)

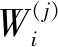
(5)監測和整合下INE(,,)的變化情況，選擇INE(,,)最小時對應的最優=(,,)，構造自適應可調品質因子小波。

(6)按照圖1重構各尺度下的各個子帶信號，以便后續提取重構后的子帶信號特征。其中，uDFT和uDFTI分別表示離散傅氏變換及其逆變換；和分別代表低通尺度變換(LPS)和高通尺度變換(HPS)的系數。

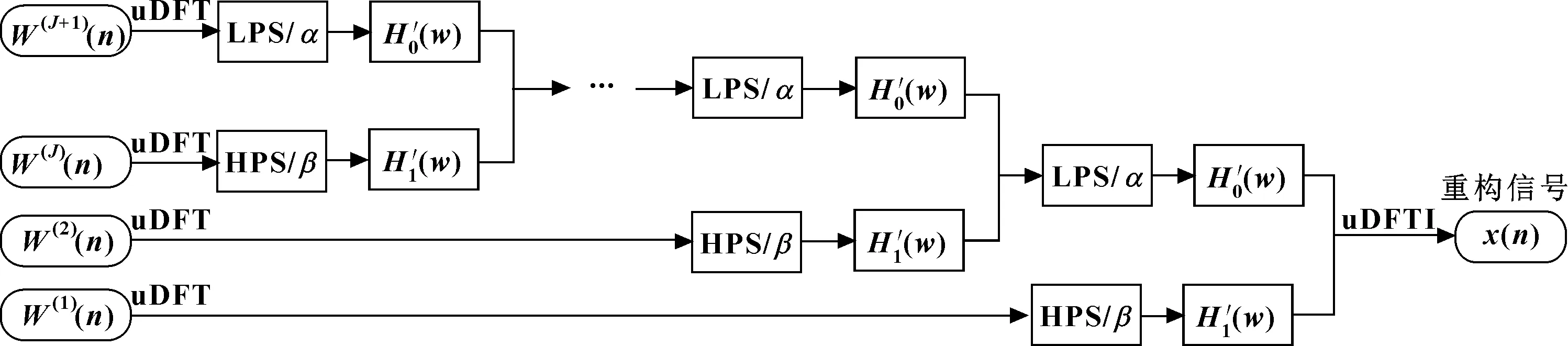
圖1 可調因子小波變換的重構過程

2 模糊熵算法

模糊熵的概念是由RICHMAN基于樣本熵提出的,模糊指數表征兩個信號的相似度，抗噪聲干擾能力很強。下面詳細說明模糊熵算法的執行過程。

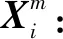
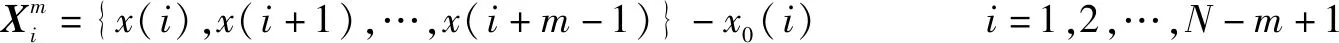
(7)

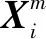
續 表4

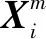
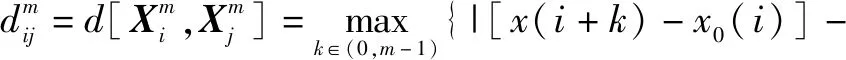
[(+)-()]|},=1,2,…,-+1,?

(8)

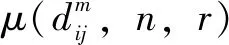
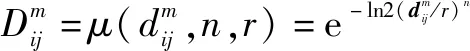
(9)

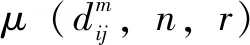
(4)計算維下的關系維度(,)：

(10)

(5)增加到+1維，重復步驟(1)～(4)得到+1(,)：

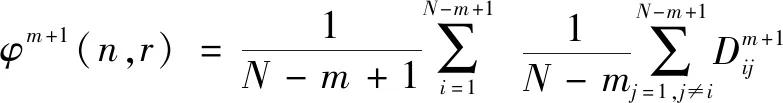
(11)

(6)模糊熵的定義為

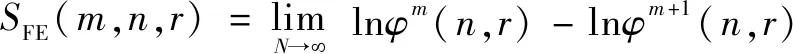
(12)

式中:若為有限值時，(,,)可表示為

(,,,)=ln(,)-ln+1(,)

(13)

3 CS-ELM算法

為提高早期故障預示準確率，針對隱層節點數的確定運用布谷鳥搜索算法進行改進。以下是CS-ELM算法的詳細步驟：

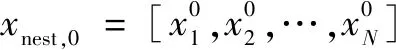
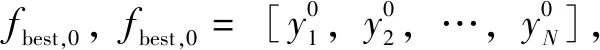
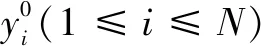
(5)為每個鳥巢中產生服從均勻分布的概率，若>，則對鳥巢的位置進行更新；

(6)若達到，停止尋優，得到和對應的，否則跳轉至步驟(4)；

(7)選出中最小的值，并獲得其對應的鳥巢位置，經過圓整后輸入到極限學習機模型中作為隱層層數，進行訓練后輸出對應的、、，并據此建立CS-ELM早期故障預示模型。 CS-ELM算法的具體流程如圖2所示。

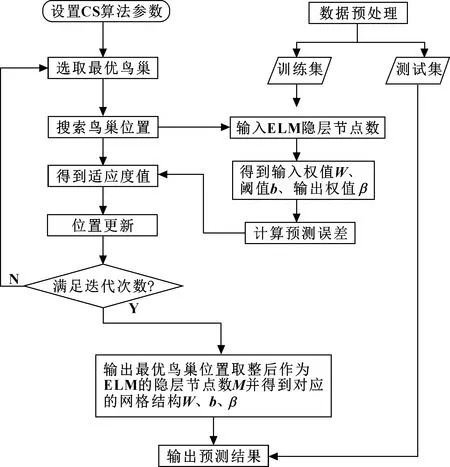
圖2 CS-ELM算法的具體流程

4 試驗分析與論證

4.1 試驗測點布置

根據規則,測點應布置在對常見故障最敏感的位置，但受供輸彈系統外形和環境的限制無法完全遵循此規則，只能選既可安裝傳感器又能準確反映故障狀況的較合適的點。此次對某中大口徑轉管火炮進行測點布置，共布置振動測點6處。現場測試時的采樣頻率為25 600 Hz，選用32Ch-LMS信號采集裝置。表1給出了測點布置位置和傳感器類型，圖3所示為測點布置示意。

表1 某轉管火炮測點布置

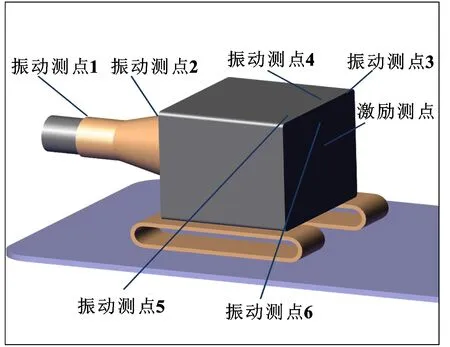
圖3 測點布置示意

4.2 試驗過程及記錄

射擊試驗的裝定射擊速度為450發/min，即兩發炮彈發射的平均時間間隔為0.133 s，以此開展該中大口徑火炮供輸彈系統的射擊試驗。具體的試驗過程如下：(1)試驗時，首先完成一次2連發和兩次6連發的射擊，射擊過程中均表現良好。(2)進行一次40連發的射擊試驗，在此次射擊過程中，雖然所有發數全部打完，但在中途第25發開始出現了射速明顯降低的狀況，圖4所示為此次試驗各發之間射擊時間間隔。本文作者將此定義為早期故障工況，同時也間接說明：步驟(1)的射擊工況處于早期故障的形成階段，經專家評估后，確認其為正常工況到早期故障的過渡階段，本文作者將它定義為早期故障的惡化工況。(3)在40連發射擊試驗之后，現場工作人員對供輸彈系統進行了檢修與維護，隨即開展了60連發和80連發的射擊工作，在炮彈發射時均未出現異常。

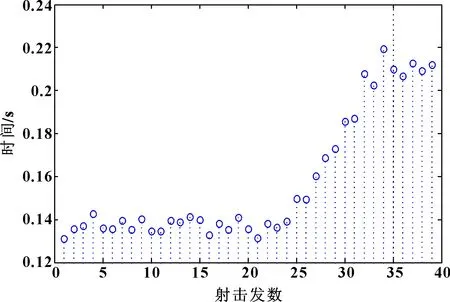
圖4 40 連發射擊試驗時間間隔統計

4.3 基于自適應TQWT和模糊熵的信號降噪和特征提取

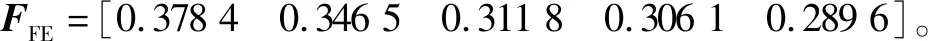
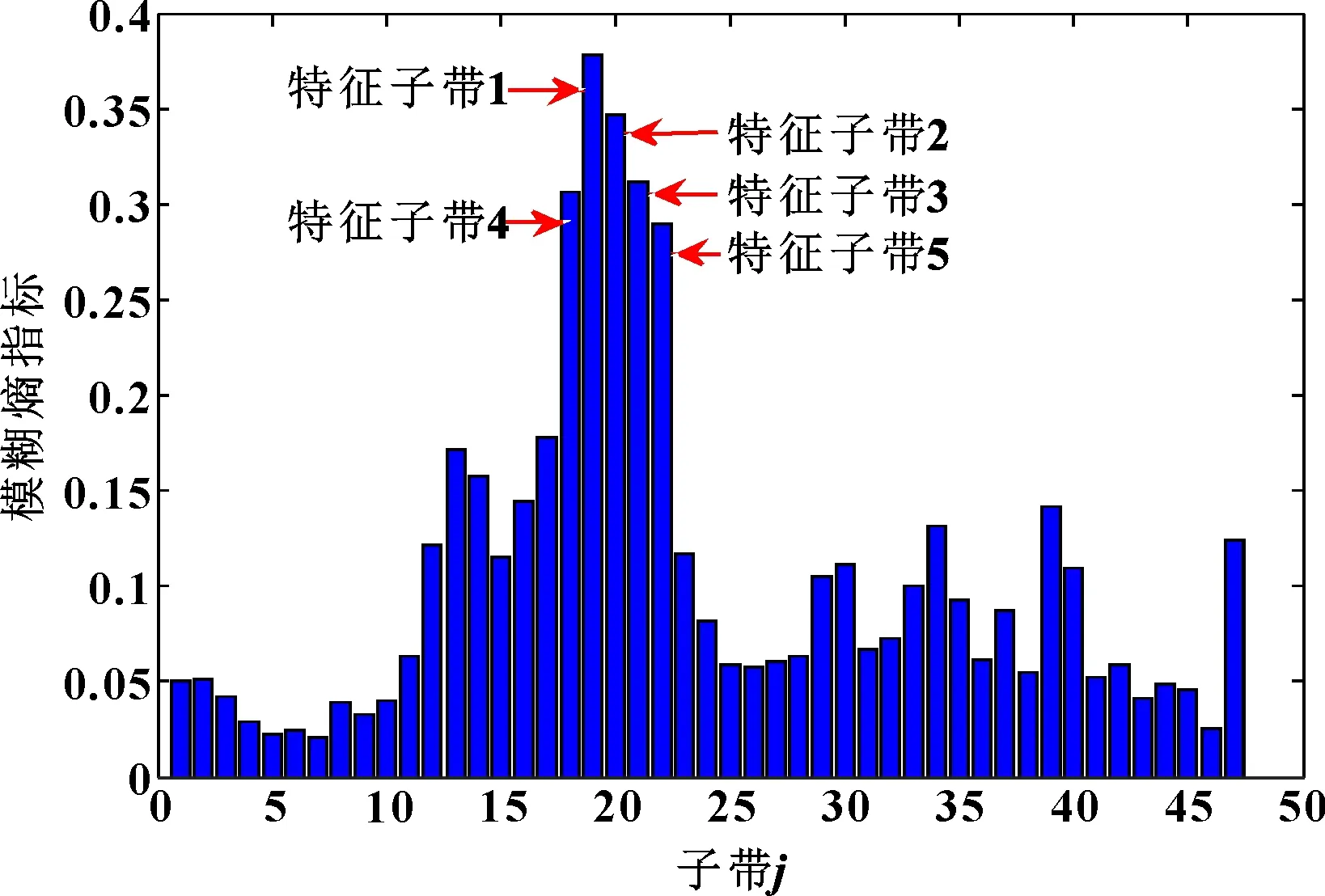
圖5 5個最優特征子帶

按照以上過程，對所有通過射擊試驗獲取的振動測點的樣本數據進行降噪和早期故障特征提取，并組成表示早期故障信息的特征向量集。振動測點3的部分特征向量如表2所示。在此每種工況僅列出5組數據特征向量。

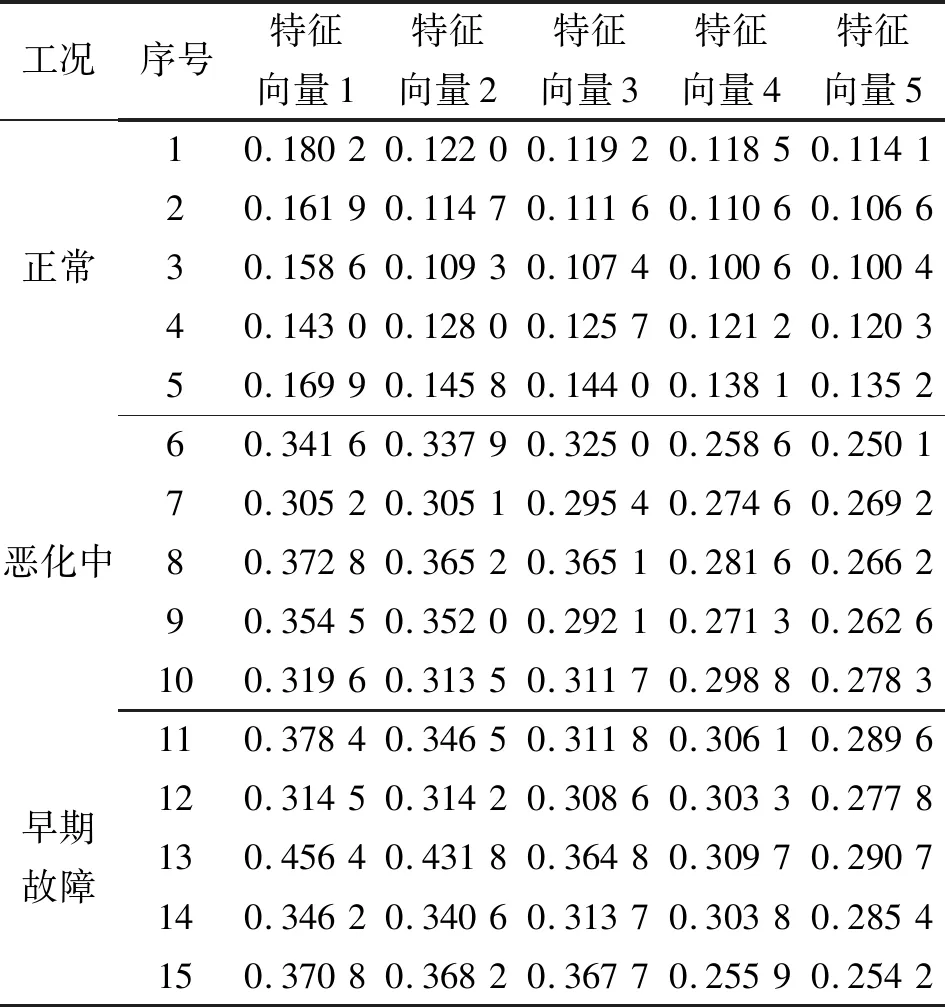
表2 振動測點3的部分特征向量

4.4 基于CS-ELM的復雜供輸彈系統故障診斷

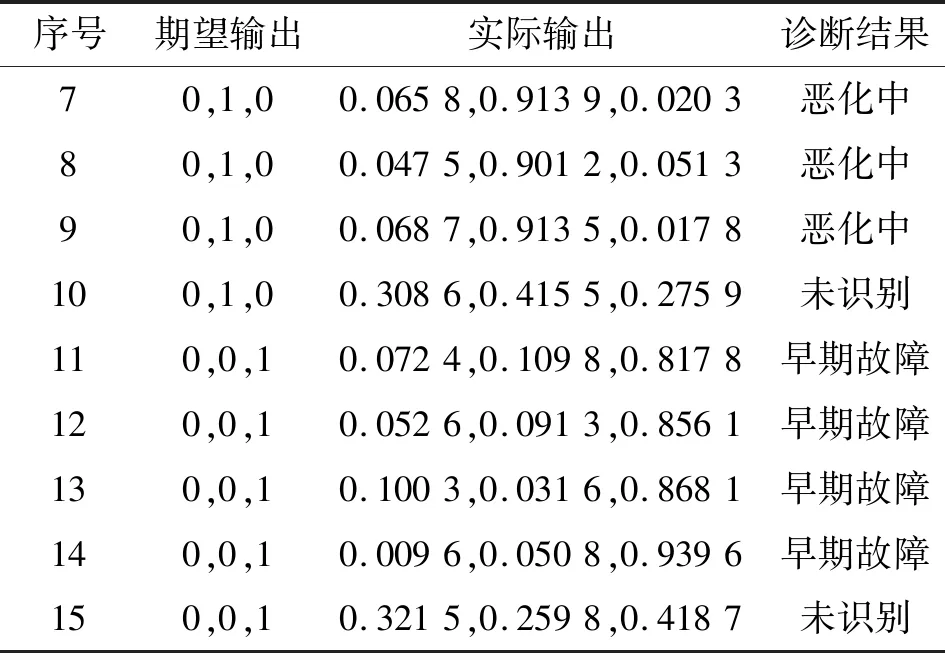
針對復雜供輸彈系統射擊試驗獲取的3種工況的3個測點的194發樣本數據分別進行分析處理，并提取表征系統早期故障狀況的模糊熵特征。每種工況隨機選取1/3的特征向量組成訓練樣本,共65個(正常工況47個、惡化中工況5個、早期故障工況13個)，輸入到CS-ELM中進行訓練，CS的參數設置為=0.25、=50。將剩余樣本的特征向量組成測試樣本129個(正常工況93個、惡化中工況9個、早期故障工況27個)，輸入到CS-ELM中進行早期故障的預示。經過CS-ELM進行早期故障識別后，表3所示為射擊試驗振動測點3的部分樣本的早期故障預示結果；同時，經ELM識別的結果如表4所示，表5所示為兩種診斷結果的對比。可以發現，經CS-ELM診斷識別的準確率達到90.7%；而用ELM的綜合準確率為86.82%，證明了CS-ELM方法的有效性。

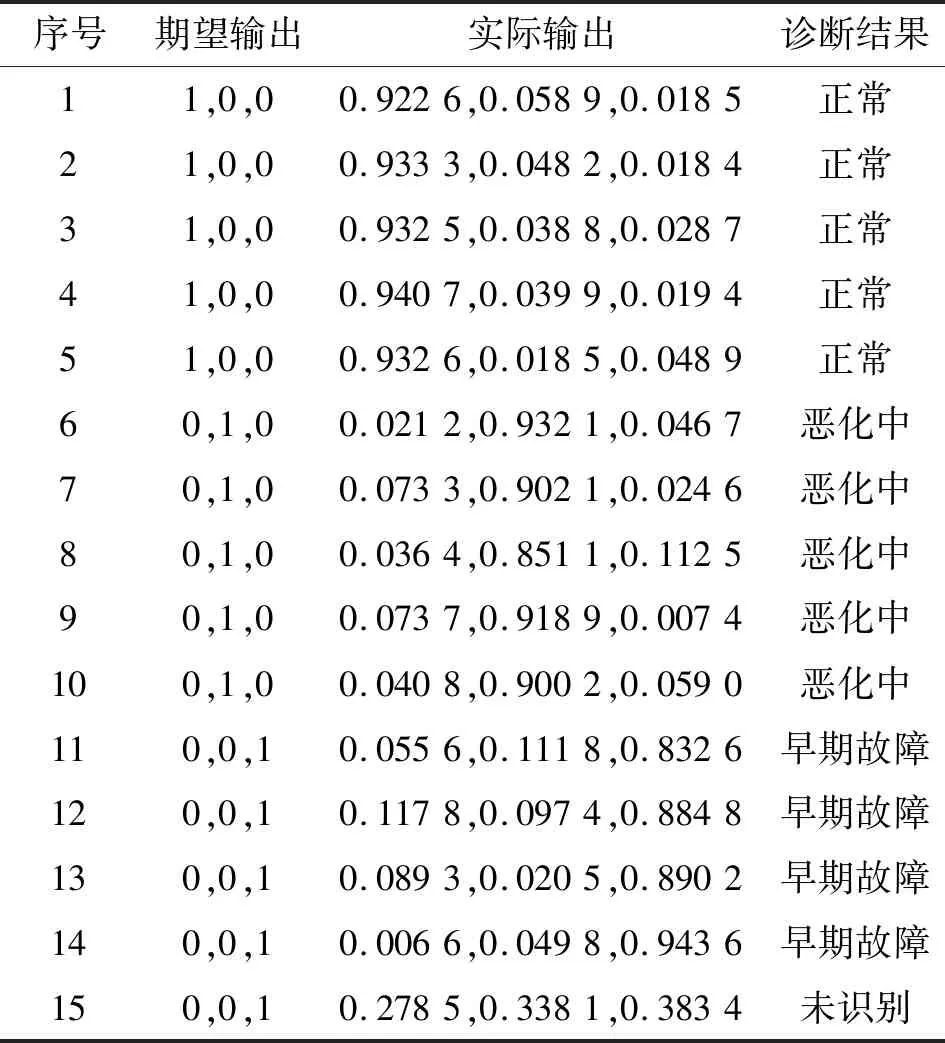
表3 振動測點3的部分樣本的早期

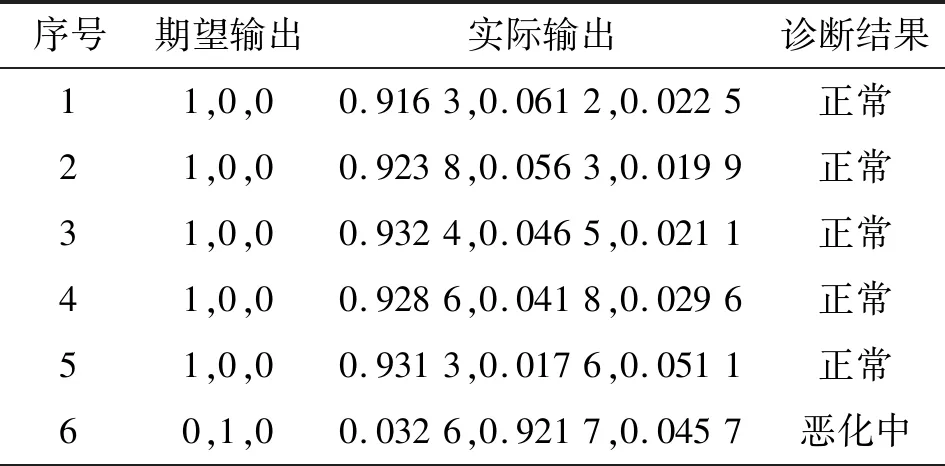
表4 振動測點3的部分樣本的早期故障預示結果(ELM)

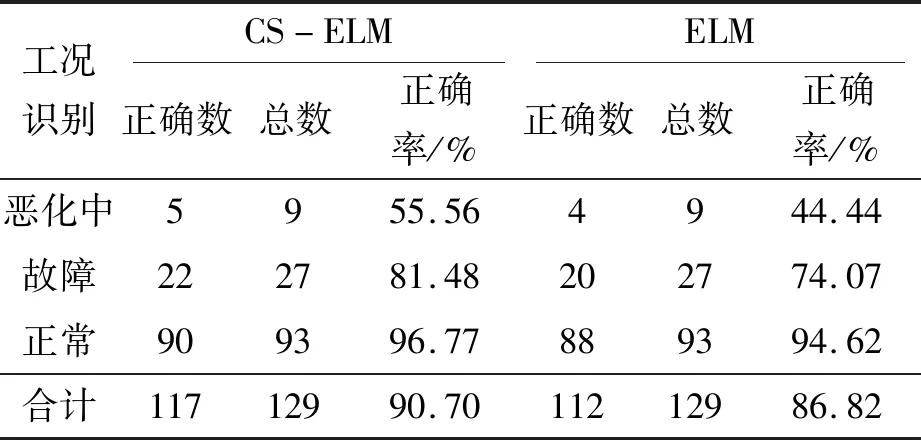
表5 診斷結果對比

5 結束語

本文作者提出一種基于模糊熵和CS-ELM的供輸彈系統故障預示方法，進行基于自適應TQWT和模糊熵的信號降噪和特征提取后，針對原始極限學習機模型中存在的缺陷，采用布谷鳥搜索算法進行改進。將所提取信號的特征向量分配為訓練樣本和測試樣本，輸入到自適應優化后的極限學習機模型中進行訓練和測試，并與未經優化的極限學習機訓練結果進行對比。結果表明：所提的方法可在一定程度上提高供輸彈系統的早期故障診斷準確率，準確率達90.7%。