基于樣本熵的改進小波降噪在微電機質量檢測中的應用

馬賢武，劉其洪，李漾，2，蘭欽泓，李偉光

(1.華南理工大學機械與汽車工程學院，廣東廣州 510641;2.佛山衡生醫療自動化有限公司，廣東佛山528225)

0 前言

微型電機廣泛運用在工業制造、家用電器等領域，需求巨大。現階段國內外對大型電機故障檢測研究較多，而對于微型電機故障檢測卻鮮有研究。目前眾多中小型微型電機生產企業仍保留傳統人工聽音的方法對微型電機進行出廠質量檢測，效率低下且誤判率高。尋找快速準確的現代化方法進行出廠質量檢測對于廠家大規模生產至關重要。由于微型電機體積小，其振動與聲音信號振幅較小，且工廠實際生產中具有復雜的背景噪聲，提取到的微型電機信號信噪比低，因此如何對提取到的電機信號進行降噪成為研究難點之一。

信號降噪的常見方法主要有傅里葉變換、短時傅里葉變換、小波去噪等。傅里葉變換將時域信息轉換為頻域，可以有效展現信號的頻率分布，但難以刻畫局部信息，對于電機信號等非穩態信號適用性較差；短時傅里葉變換在傅里葉變換的基礎上進行了加窗，具有一定的局部分析能力，但由于固定窗函數的限制，無法滿足非穩態信號變化的頻率需求。小波去噪由DONOHO在1995年提出，通過選取適當的閾值修改信號的小波分解系數來達到去噪目的，由于它自身良好的局部時頻分析能力被廣泛運用在非線性非平穩信號降噪領域的研究。

小波閾值降噪的關鍵在于閾值函數的選取，其數學性能在一定程度上決定了降噪的效果。傳統的閾值函數有硬閾值和軟閾值，但均有一定的局限性。硬閾值函數由于函數的不連續性，在降噪過程中容易產生跳變和振蕩；軟閾值函數重構精度不高，可能造成信號過度失真。近些年，閾值函數的改進也是信號處理研究的熱點之一。文獻[7]提出了一種軟硬閾值折衷函數，降噪效果有一定的提升，但函數仍不連續。文獻[8-9]提出了一種基于e指數或log底數的閾值函數，解決了函數連續性的問題，但缺乏調節因子，靈活性較差。文獻[10]引入了調節因子、，實現了閾值函數的可調節，但并沒有說明調節因子的取值依據，且計算較為復雜。

針對現階段閾值函數的缺陷，本文作者提出了一種以樣本熵為調節因子的新閾值函數，能夠根據處理信號的噪聲復雜程度自動調節閾值函數；仿真驗證結果表明：改進閾值函數能夠有效去除噪聲信號，降噪效果相比于傳統閾值函數得到了顯著提升。最后采用改進的閾值函數對微型電機異音信號進行降噪，并提取相應的時域特征結合SVM分類器對它進行質量檢測。該方法旨在為微型電機故障檢測提供理論依據與思路。

1 小波閾值去噪原理與計算

1.1 小波閾值去噪原理

小波降噪基本原理為：先將信號進行若干層的小波分解，信號的不同細節特征將會體現在變換后的小波系數上。根據非平穩信號的特點，一般噪聲信號主要集中在幅值較小的系數中，而有用的信號集中在幅值偏大的小波系數中。再通過選取合適的閾值，將低于閾值的小波系數舍棄，保留高于閾值的小波系數，達到降噪的目的。

小波降噪的步驟主要由3個部分組成：(1)對原始信號進行小波分解。針對所研究的信號相關特性選取合適的小波基及相應的分解層數。(2)閾值處理。對分解得到的各尺度小波系數采用相應的閾值函數進行閾值處理。(3)小波重構。對經過閾值處理過的小波系數進行重構，得到降噪后的信號。

1.2 常見閾值函數

傳統的閾值函數一般有軟閾值函數和硬閾值函數，其表達式如下：

(1)硬閾值函數

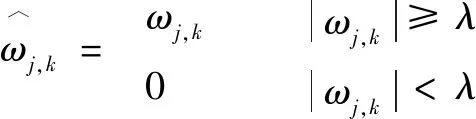
(1)

(2)軟閾值函數

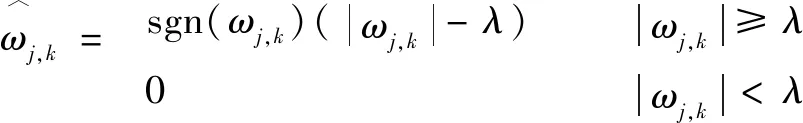
(2)

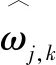
軟、硬閾值函數在實際工程中得到了廣泛的運用，具有一定的降噪效果，但隨著信號的復雜程度增加，上述閾值算法也表露出很大的不足。硬閾值函數在處并不連續，存在間斷點，導致信號重構時容易產生跳變和震蕩；軟閾值函數雖然整體連續，但由于對高于閾值部分的小波系數進行了收縮處理，從而重構信號與原始信號產生恒定偏差，容易導致部分信息失真，誤差較大。

針對傳統閾值函數所存在的不足，文獻[9]提出了一種逼近對數型閾值函數，其函數表達式如下：

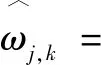
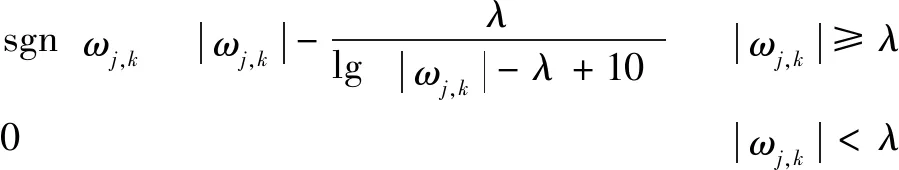
(3)

該算法解決了連續性和恒等偏差的問題，經過仿真驗證，降噪后信號信噪比相比傳統閾值函數有了較大的提升，但該函數只對前半部分進行了改進，在處平滑性較差，且不含調節因子，無法根據各種處理信號的實際特點進行靈活調整。針對此，文獻[10]中進行了相應的改進，其表達式如下：

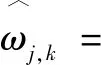
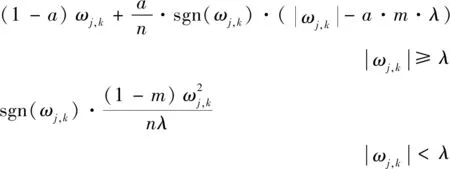
(4)

該式引入了調節因子、，且對閾值函數進行了整體改進，但作者并沒有對、取值依據進行闡述，若依據信噪比最優進行排選，則計算量較大。

2 改進閾值函數與仿真

2.1 改進閾值函數分析

為克服上述閾值函數的不足，本文作者提出了一種基于樣本熵(Sample Entropy，SampEn)調節因子的改進閾值函數，其表達式如下：

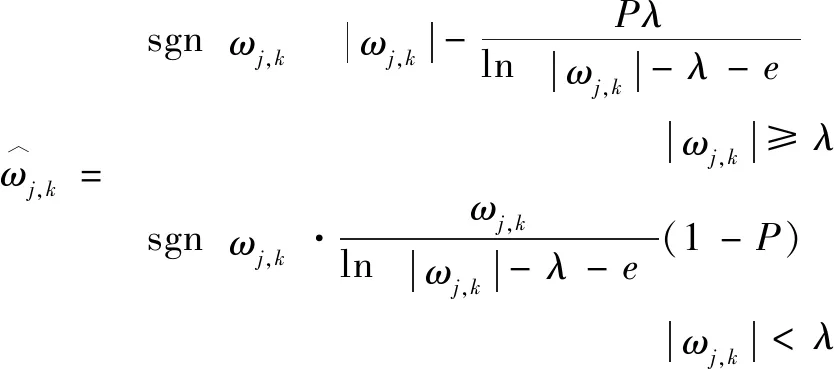
(5)

式中各參數與公式(2)相同，為調節因子，其取值范圍為(0,1)。

該公式具有以下數學特性：

(1)該式具有連續性。

當|,|→時：

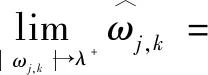
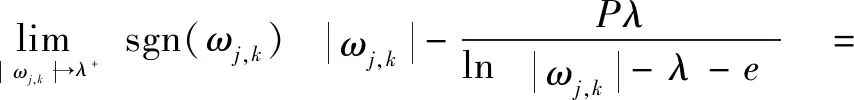
-=(1-)

(6)

當|,|→時：

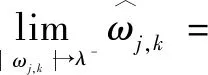
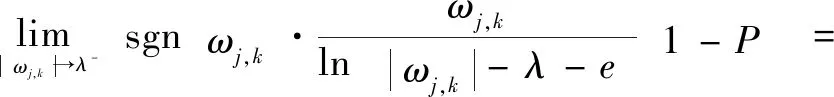
(1-)

(7)

公式在±處連續得證。

(2)該式偏差性較小。

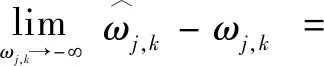
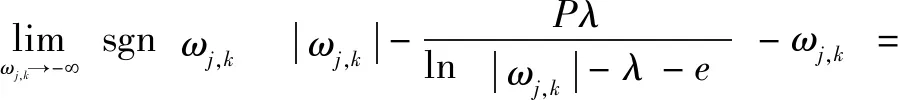
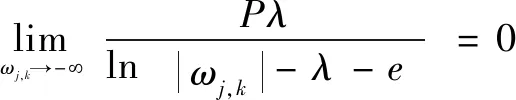
(8)

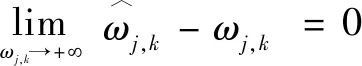
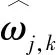
(3)該式具有漸進性。

當,>0時：

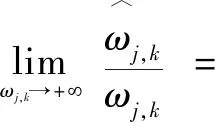
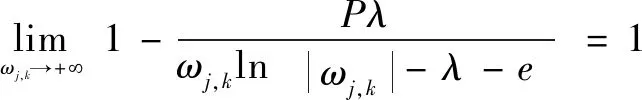
(9)

同理,當,<0時：

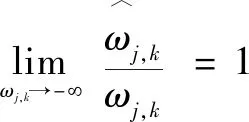
(10)

該式隨著|,|不斷增大，逐漸趨向于,。

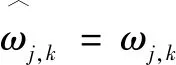
2.2 基于樣本熵的調節因子

針對不同信號的特征，選取不同的小波基,閾值函數降噪效果也不盡相同，本文作者引入樣本熵來對閾值函數進行靈活調整。

樣本熵由20世紀末幾位非線性動力學研究者提出，它通過度量信號中產生新模式的概率大小來評估時間序列復雜性，樣本熵的值越低，序列自我相似性就越高；反之，就越復雜。其計算原理如下：

對于由個數據組成的時間序列{()} =(1),(2),…,()，樣本熵的計算方法如下：

(1)按序號組成一組維數為的向量序列，其中()={(),(+1)，…,(+-1)},1≤≤-+1。

(2)定義向量()與()之間的距離[(),()]為兩者對應元素中最大差值的絕對值。即：

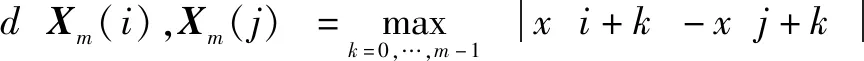
(11)

(3)對于給定的()，統計()與()之間距離小于等于的(1≤≤-,≠)的數目，并記作。對于1≤≤-，定義：

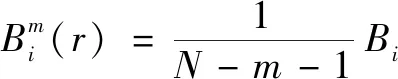
(12)

(4)定義()()為

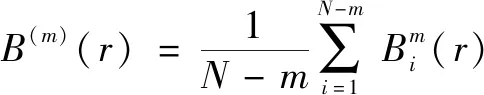
(13)

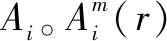
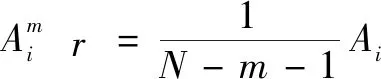
(14)

(6) 定義()為

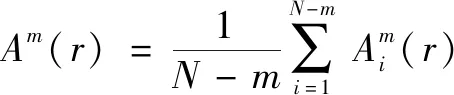
(15)

這樣()()是兩個序列在相似容限下匹配個點的概率，而()是兩個序列匹配+1個點的概率。樣本熵定義為

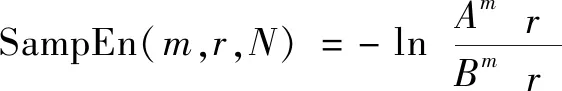
(16)

令：

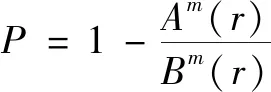
(17)

的取值范圍為[0,1]，大小與樣本熵正比相關，其值越大，表明該信號系數序列越復雜，所含噪聲也越多；反之，該信號系數排列越規律，所含噪聲也越少。觀察式(5)可知，當取值越趨向于1時，改進函數趨向于收縮能力更強的軟閾值函數，能夠去除更多的噪聲信號；當趨向于0時，改進函數越趨向于偏差較小的硬閾值函數，能夠保留更多有用信號。無論取何值，函數整體始終保證連續可導，既克服了傳統函數的相應缺點，也可根據不同信號的樣本序列復雜度來進行降噪，具有較強的適應性。

2.3 仿真信號結果與分析

為了驗證文中提出的改進函數的降噪效果和可靠性，采用MATLAB軟件對信號進行仿真試驗。樣本信號采用MATLAB自帶的heavy sine信號，采樣點數為2 048，并加入高斯白噪聲來模擬噪聲信號。分別采用硬閾值函數、軟閾值函數、文獻[9]中改進函數、文中改進函數對模擬信號進行降噪，小波基采用db4小波，分解層數3層，閾值選取參考文獻[15]。仿真結果如圖1所示。

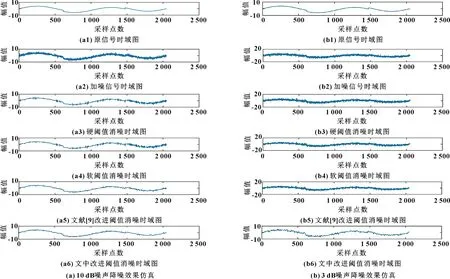
圖1 不同信噪比噪聲降噪效果仿真

圖1反映了不同信噪比環境下不同閾值函數的降噪效果。圖1(a)為加入了10 dB高斯白噪聲的降噪效果圖，可知:軟、硬閾值函數均有一定的降噪效果，其中軟閾值函數降噪效果略好于硬閾值函數，文獻[9]提出的改進閾值函數降噪效果較傳統閾值函數得到了較大提升，細節仍產生少許震蕩，這是由于該閾值函數在閾值處平滑性較差。文中所提出的改進閾值函數(為0.124 2)相比以上3個函數，降噪效果最優，所重構的信號完整性較好，高斯白噪聲在一定程度上得到了去除。圖1(b)為加入了3 dB高斯白噪聲的降噪效果圖，程序計算該信號為0.436 3，遠高于圖1(a)信號，說明該含噪信號復雜度較高，較為混亂。觀察圖1(b)可知:在低信噪比環境下，軟、硬閾值均不能達到較好的降噪效果，甚至文獻[9]提出的改進閾值函數降噪效果也不理想。文中提出的改進閾值函數降噪效果明顯優于其他函數，在信號混亂復雜的情況下也能基本提取有效信號信息。根據仿真結果可知，基于樣本熵的改進閾值函數無論在高信噪比還是低信噪比環境下，降噪效果都明顯優于傳統的閾值函數，尤其在復雜度較高的含噪信號中也能一定程度保留有用信號，具有較強的靈活性和適用性。

為了進一步對去噪效果進行定量說明，采用信噪比(SNR)和均方根誤差(RMSE)兩個指標進行說明。兩個指標公式如下所示：

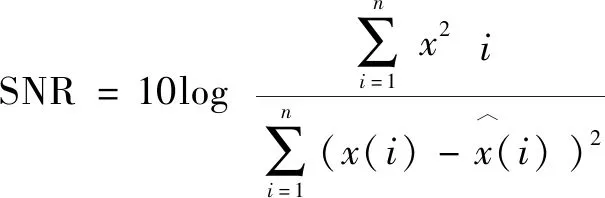
(18)

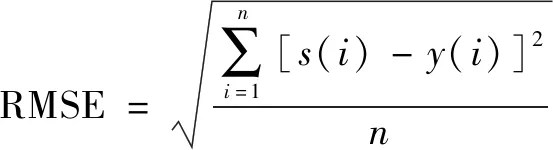
(19)

其中：()表示原始信號，()表示去噪后的信號。

對于降噪效果而言，SNR越大，RMSE越小，表明信號的降噪效果越好。數據結果如表1所示。

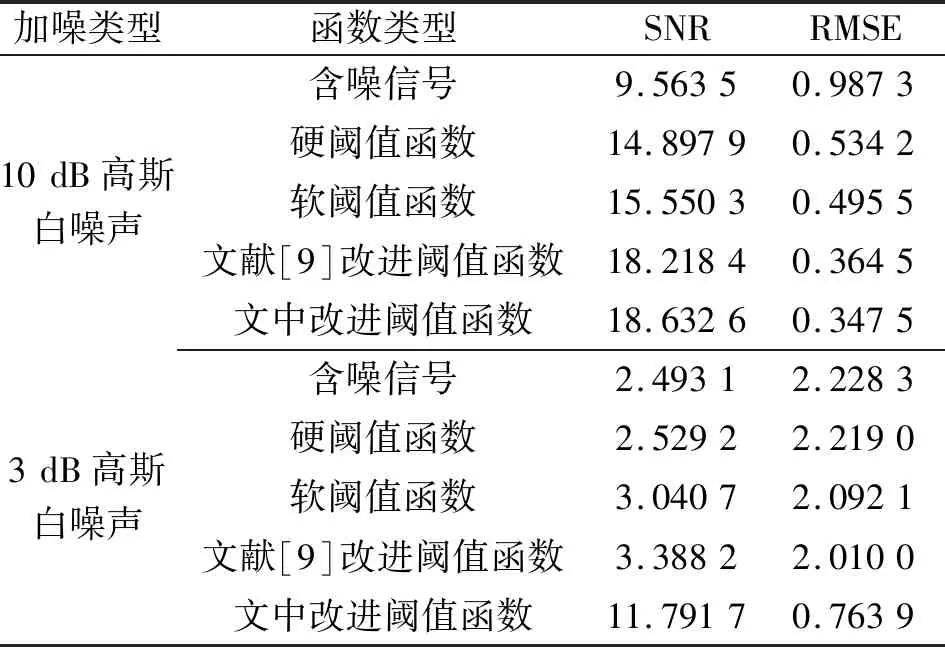
表1 各種閾值函數降噪SNR、RMSE對比

表1結果與圖1結果一致。在高信噪比(10dB)環境下，傳統閾值函數和改進閾值函數均取得了一定的降噪效果，其中文中提出的改進閾值函數降噪效果最優，SNR最大，RMSE最小。對于低信噪比(3 dB)環境，無論是硬、軟閾值函數還是文獻[9]提出的改進閾值函數降噪效果均不理想，文中的改進閾值函數降噪效果明顯優于其他函數，有效保留了原始信號特征。仿真結果表明：本文作者提出的改進閾值函數適應性強，可靠性高。

3 微型電機質量檢測實例研究

3.1 試驗方案

為了進一步驗證改進小波閾值函數降噪在實際工程中的有效性，采用微型電機作為實例進行診斷。由于微型電機體積小，信號微弱，在實際運用中采用振動傳感器對其進行信號采集安裝極其不便，因此本文作者擬采用聲音傳感器對其聲音信號進行收集。微型電機生產廠家對其進行出廠診斷時，只需對其優劣進行判斷，并不需要對其故障類型進行分類。針對微型電機信號，最主要的就是去除環境噪聲，保留電機特征信號，即可對其優劣進行判斷。

采用提出的基于樣本熵的改進小波閾值函數對微型電機聲音信號進行降噪處理，再提取有效信號的不同時域特征值，采用SVM分類器對樣本數據進行訓練，從而對微型電機優劣進行判斷。采用的微型電機型號是R370-FT-50079W，結構如圖2所示，采用24 V電源供電。聲音信號的采樣頻率為22 kHz，遠高于電機工作信號的頻率，確保不會失真。

圖2 微型電機結構

3.2 試驗結果

分別選取15個良品樣機、15個不良品樣機作為訓練集，采樣時間為1 s，將采樣后的聲音信號采用改進小波閾值降噪，提取均方根值、絕對平均值、信號方差3個時域特征為樣本特征，輸出-1代表不良品樣機，1代表良品樣機。電機信號降噪前后時域圖如圖3所示，訓練特征見表2。

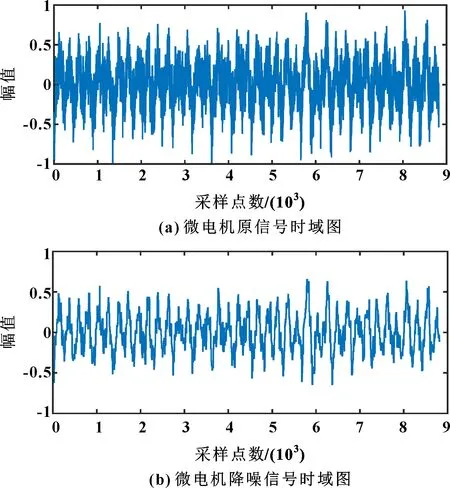
圖3 良品1降噪前后時域圖

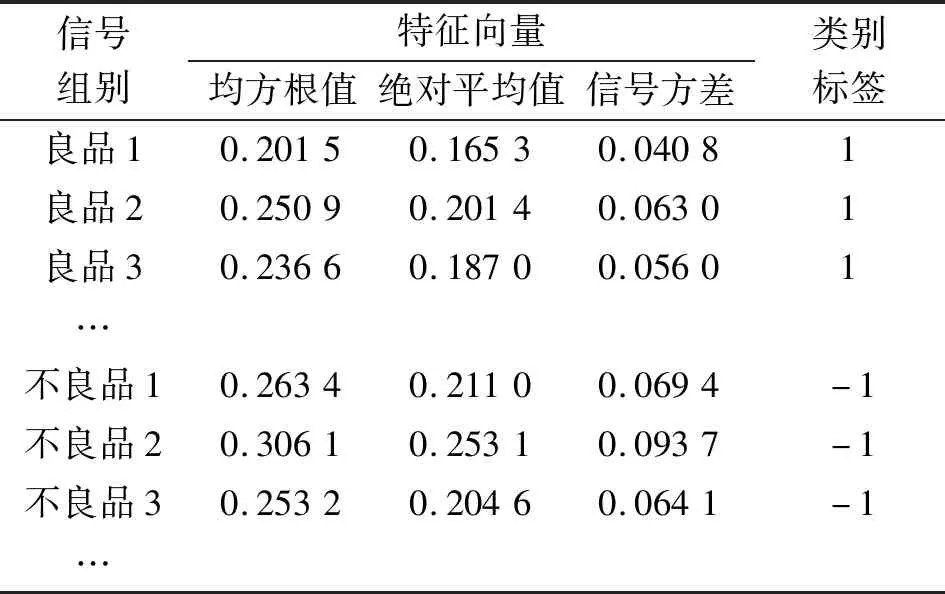
表2 訓練集特征

觀察圖3可知，經過改進小波閾值降噪，微型電機噪聲信號得到了有效去除，時域特征更加明顯。

選取10個微型電機樣品作為測試樣本，代入已經訓練好的SVM分類器中，試驗結果見表3。

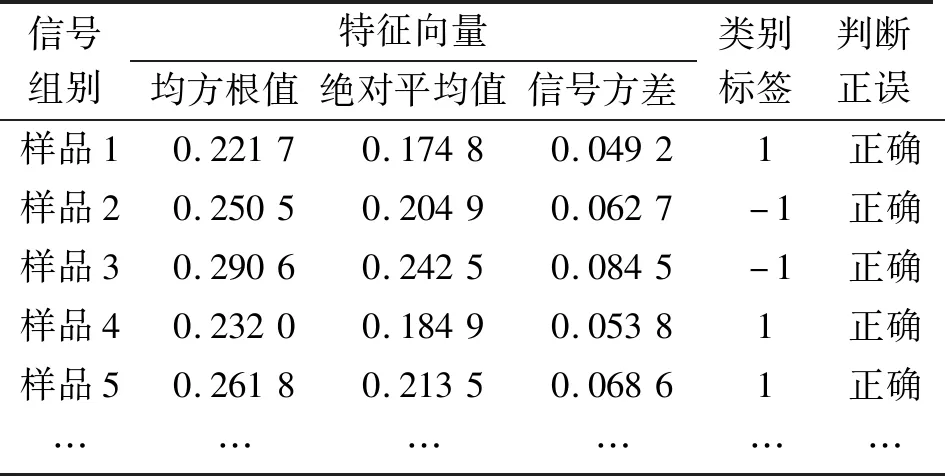
表3 測試集試驗結果

根據表3試驗結果，10組測試樣本均成功判斷，說明提出的方法能夠有效對微型電機出廠質量優劣進行診斷。

4 結論

針對傳統小波降噪閾值函數連續性差、降噪效果穩定性差等問題，提出了一種基于樣本熵的改進小波閾值函數，能夠根據信號復雜度自動調節閾值函數，并證明了該函數連續性、偏差小等數學特性。仿真試驗結果和信噪比測試表明：本文作者提出的閾值函數能夠有效地對噪聲信號進行去除，尤其在低信噪比環境下，降噪效果明顯優于軟、硬閾值函數和文獻[9]中提出的改進閾值函數。

為了驗證該閾值函數在工程運用中的有效性，采用改進小波降噪方法對微型電機信號進行降噪，提取均方根值、絕對平均值、信號方差3個時域特征為樣本特征，結合SVM分類器進行訓練，選取10個樣本電機作為測試樣本進行測試，判斷結果均正確。試驗結果表明：改進的小波降噪算法能夠有效去除電機信號環境噪聲，提取有效的信號特征，從而對其優劣進行判斷。