粒子群算法優化的液壓球形關節自抗擾控制研究

任洵濤,邊斌,王亮

(1.中國船舶集團有限公司第七〇四研究所，上海 200031；2.北京航空航天大學自動化科學與電氣工程學院，北京 100191)

0 前言

球面運動作為一種僅次于旋轉運動的重要運動類型，在工業生產中得到了廣泛應用，如靈巧眼和機器人關節，目前其主要實現形式有串聯機構和并聯機構。串聯機構存在關節累計誤差大、末端定位精度低和剛度小的缺點，而并聯機構往往工作空間較小，存在較多奇異位形。液壓球形關節作為一種球面運動機構，不需要中間傳動裝置，僅通過單一關節便可以實現兩個自由度的光滑球面運動，具有結構緊湊、轉動慣量小和剛度大等優點。

集成式的液壓球形關節系統具有多輸入多輸出、非線性和模型不確定性等特點，雖然傳統PID控制具有結構簡單和易于實現的特點，但是很難滿足這種復雜非線性系統的控制需求。自抗擾控制(Active Disturbance Rejection Controller，ADRC)作為一種不要求系統精確動力學模型的控制方法，在系統動力學模型難以精確建立和非線性系統的控制中得到了廣泛應用。劉春強等在永磁同步電機伺服系統的控制中采用三階擴張狀態觀測器，設計了位置-電流雙環非線性ADRC，取得良好的控制效果。姜偉等人為了削弱時變擾動和模型不確定性的影響，在工業機器人關節伺服控制系統設計過程中，提出了一種基于慣量估計的變增益ADRC，提高了系統的動態性能。

然而，非線性ADRC引入了非線性項，需要調節的參數較多，且整定困難，限制了其在實際工程中的應用。為了能夠有效調節參數，齊曉慧等利用BP神經網絡對擴張狀態觀測器(ESO)的參數進行在線調整，提升了系統的抗干擾能力，但是受BP神經網絡設計質量的影響，有一定的局限性。李揚等人利用動態響應過程中時序數據關聯關系挖掘的方法對自抗擾控制中誤差反饋律參數進行整定，并未對ESO參數進行自整定。王麗君等在雙輸入雙輸出熱連軋板寬板厚控制系統設計過程中，利用具有全局快速搜索能力的變尺度混沌優化方法對ADRC參數進行優化，一定程度上提升了ADRC的抗擾能力。

綜上，利用智能優化算法對ADRC參數進行整定是一個研究的熱點。本文作者在液壓球形關節控制系統設計過程中，采用一種以時間乘以絕對誤差積分為優化準則(ITAE)的改進型粒子群優化(Particle Swarm Optimization，PSO)算法，對ADRC的參數進行在線自整定。介紹液壓球形關節的結構，建立其動力學模型；介紹非線性自抗擾控制器的原理，分析改進型PSO算法的優化過程，并將改進型PSO融合到ADRC參數調整過程中；通過MATLAB/Simulink進行仿真研究，驗證算法的有效性。

1 液壓球形關節結構及工作原理

圖1所示為液壓球形關節結構，它具有繞軸旋轉角的偏轉和繞軸旋轉角的橫滾兩個自由度，可以實現以點為中心的球面運動。該機構主要由下定子、舵葉、滑軌、上定子、上轉子和下轉子等組成，所有球形構件具有相同的中心。

圖1 液壓球形關節結構示意

作為執行機構的回轉馬達和擺動馬達集成在舵葉和轉子上，其中，回轉馬達是一個超全周馬達，可以實現超全周運動，如圖 2所示。向滑軌和向滑軌通過軸承安裝在上定子上，其與編碼器組成了轉角測量系統，利用滑軌實現運動在和方向上的定向，通過編碼器測量轉動角度。同時，兩個馬達的進油口和回油口均布置在舵葉軸上，與舵葉軸上布置的密封圈和配流帽形成了兩套獨立的配油系統。

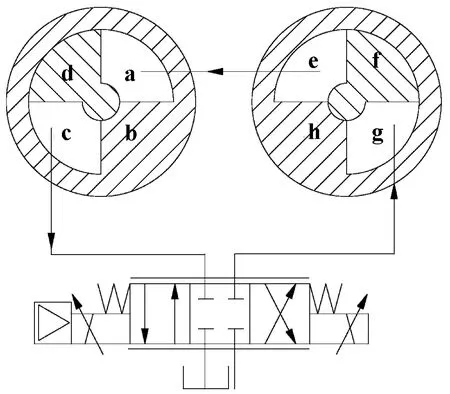
圖2 回轉馬達原理

2 液壓球形關節動力學模型

將=[]作為廣義坐標系建立液壓球形關節的動力學模型，可表示為

(1)

根據液壓球形關節工作原理可知，活動部件分別為舵葉、轉子和回轉馬達，其轉動角速度分別為

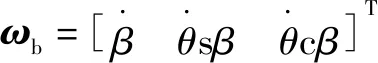
(2)

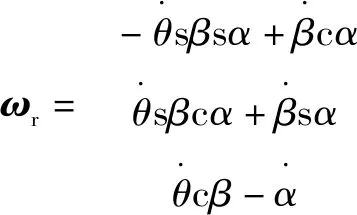
(3)

(4)

式中：為轉子繞定子坐標系軸的轉動角度。c和s分別代表cos和sin。

利用拉格朗日法可以求得液壓球形關節的動力學模型：

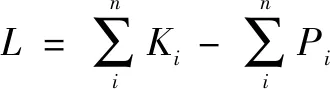
(5)

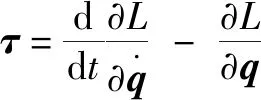
(6)

=diag(,,,)

(7)

式中：為拉格朗日函數;和分別為運動部件的動能和勢能，=b,r,m;代表運動部件的轉動慣量。

=+secc(tan+c)[sec-(tan+c)]

==tansc(tan+c)[sec-

05(tan+c)]

=+tans)tan+c)

=0

=-(++)s

3 自抗擾控制的基本原理

自抗擾控制是韓京清研究員提出的一種結合現代控制理論成果和PID思想精髓的非線性控制器，將系統未建模動態和外界擾動等未知信息均視為擾動，通過輸入輸出信息進行估計并補償，以實現動態估計和反饋補償。它主要由跟蹤微分器(TD)、擴張狀態觀測器和非線性狀態誤差反饋控制律(NLSEF)組成，如圖 3所示。跟蹤微分器可以從含有噪聲的信號中提取出實際信號，降低甚至消除噪聲對信號的影響，同時給出近似的微分信號。

圖3 ADRC結構

3.1 擴張狀態觀測器設計

引入擴張狀態后，以運動方向為例進行計算，式(1)所示的液壓球形關節動力學模型的狀態空間表達可擴張為

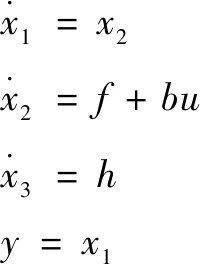
(8)

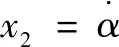
針對上式設計非線性擴張狀態觀測器為

(9)

式中：

(10)

引入誤差閾值可以把||sgn()改造成在原點附近具有線性段的連續的冪次函數，避免小誤差時由高增益引起的高頻顫振現象。通常?=05、?=025，一般以0.01為基點進行調節。、和為觀測器增益系數，和越大跟蹤信號的速度越快，同時可以抑制過大產生的系統振蕩；越大估計的擾動相對于實際滯后越小。

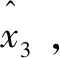
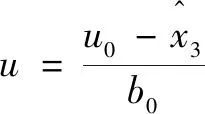
(11)

則：

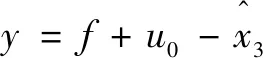
(12)

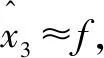
小學數學是一門基礎性的課程，對學生今后很多方面知識學習都有著中重要的幫助。而在小學數學教學中，開展綜合實踐活動課，提高了小學生的綜合實踐能力，但教學過程中依舊面臨著一些教學問題，這就需要使用有效的措施進行改進，解決存在的各種問題，提高整體的教學質量。

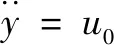
(13)

上述動態線性化過程將系統轉化為積分串聯型系統，此時可以進行基于誤差的線性或非線性反饋控制律的設計。

3.2 線性狀態誤差反饋控制律設計

為簡化設計，采用PD控制作為誤差反饋控制律：

=+

(14)

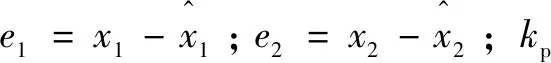
則閉環傳遞函數為

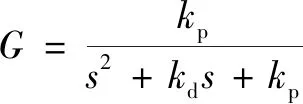
(15)

所以，增益可以設計為

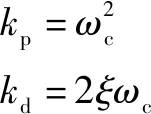
(16)

因此，擴張狀態觀測器需要整定的參數為、、和。如果系統未建模動態和參數偏差較大，會嚴重影響其他參數的整定效果。目前，沒有系統性的參數整定方法來指導這些參數的調節，仍然以手動調節為主，工作量較大且效果不佳。本文作者采用一種改進型PSO整定ADRC參數，實現參數的在線自動優化。

4 基于改進型PSO的參數自整定ARDC

4.1 粒子群優化算法

粒子群優化算法是一種模擬自然界生物覓食規律，借助過程中個體和種群信息流，從一組隨機初始解出發開始尋優的方法，它具有算法簡單、計算效率高的優點，廣泛應用于參數在線尋優的問題。其數學表達如下：

(17)

(18)

4.2 算法的改進

慣性權重用于調節對解空間的搜索范圍，其值越大，全局搜索能力越強，易得到全局最優解；反之，容易陷入局部最優，所以取值對PSO算法的參數優化效果至關重要。常用的線性遞減策略容易出現過早收斂的問題，本文作者采用改進的非線性動態方式更新，此方法與線性遞減策略相比，全局和局部搜索能力均較強，收斂速度和穩定性更好。公式為

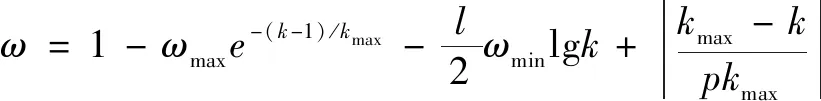
(19)

式中：和分別為最大和最小慣性權重;為最大迭代次數;為當前迭代次數;和為控制因子。

4.3 基于改進型PSO算法的ARDC參數優化

利用改進型PSO算法對ADRC參數進行在線優化整定，采用時間乘以絕對誤差積分(ITAE)作為優化性能評價指標：

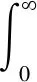
(20)

將、、和4個參數作為PSO的粒子，則基于PSO參數優化的流程如下：

(1)初始化粒子群，隨機產生粒子的位置和速度，設定粒子群算法的參數；

(2)將初始值代入到控制器并計算評價性能指標ITAE，判斷是否滿足判定條件，滿足則結束，不滿足則繼續進行步驟(3)；

(3)根據當前適應度函數值和個體與全局最佳位置，確定個體最佳位置和全局最佳位置g；

(4)根據位置和速度迭代計算公式更新粒子的位置和速度，并返回步驟(2)。

5 仿真研究

為驗證基于改進型PSO算法的ADRC參數優化算法的有效性，針對液壓球形關節的運動控制問題，利用MATLAB中的Simulink工具箱對所采用的控制器進行仿真研究。控制算法流程如圖 4所示。

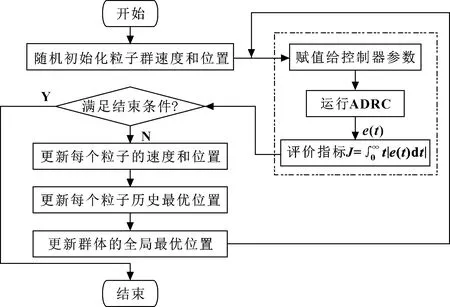
圖4 基于改進型PSO算法的ADRC參數優化算法流程

在和方向分別采用幅值為1 、0.785 rad的階躍信號作為輸入信號。控制器中PSO和ADRC的參數見表1。

表1 PSO和ADRC參數

基于改進型PSO算法優化前后液壓球形關節系統在和方向的階躍響應曲線分別如圖5和圖6所示。自優化過程中、、和的參數自整定過程如圖7和圖8所示。由圖5、圖6可以看出：與傳統的ADRC比較，經過改進的PSO優化的ADRC在和運動方向上超調量分別減小約0.3、0.13 rad，調節時間分別縮短了約0.98 s和0.59 s。因此，使用改進PSO算法優化ADRC的參數對控制器進行尋優是一種可行的方法。

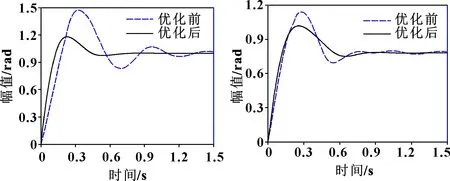
圖5 α階躍響應曲線 圖6 β階躍響應曲線

圖7 α參數優化迭代 圖8 β參數優化迭代

6 結論

以液壓球形關節為研究對象，針對其多輸入多輸出、非線性和模型不確定性等特征，ADRC需整定參數多的問題，采用一種基于改進型PSO算法對ADRC參數進行在線自整定的方法，對控制性能進行尋優。通過MATLAB/Simulink建立了控制系統模型，仿真結果驗證了算法的有效性。相比手動參數調節的ADRC，基于改進型PSO參數自整定的ADRC具有更小的超調量和更短的調節時間，性能更優越。因此，利用改進型PSO對ADRC參數尋優是一種提升控制器性能的有效方法。