巧用計數器，讓豎式除法教學厚重起來
——以“除數是一位數的筆算除法”一課為例

黃興發

(廣德市實驗小學教育集團西校區 安徽宣城 242200)

豎式除法學習對二三年級的小學生來說是一個挑戰，因為豎式除法表達方式有些“怪異”，顛覆了學生對所學的加、減、乘豎式計算的固有認識，學生理解起來有一定的思維難度。為了突破這一難點，教師習慣采用分小棒的方法，直觀形象，效果不錯。但筆者認為，除法的計算過程就是數位的轉換和數位上數值的分與合的過程，而使用計數器能夠合理表達除法的運算過程，使運算過程更加直觀。故筆在“除數是一位數的筆算除法”一課的教學中引入計數器，收到了很好的教學效果。接下來，筆者根據課堂教學實踐談一些粗淺的認識。

一、以計數器明算理，通算法

究其實質，除法是一個平均分的過程，就是把一個數位上的數值按要求平均分，如果有“余數”，就把它的計數單位變小和低一級上的數合并繼續分。借助計數器不僅能形象直觀地表達平均分的過程，更將思維聚焦在計數單位的轉換上，溝通算理算法。

教學片段：

師：請說說52÷2=是怎么計算的。

師在黑板上貼出磁性計數器并在相應的數位下板書除法豎式。(見圖1)

生：先分十位上的珠子，5顆珠子平均分成2份。

師：5顆珠子怎么平均分成2份？

生：分2份，一份2顆，還多1顆。

師：這一步除法豎式怎么寫？

生：十位上商2，二二得4，寫在5的下面，5減4得1。

師：2為何寫在十位上？余數1寫在哪位上？

生：因為這5顆珠子在十位上，表示50，平均分兩份，每份是20還余10，所以這里的商2和余數1都要寫在十位上。(見圖2)

師：這位同學講得真好，那么接下來怎么分呢？

生：將十位上剩下的1顆珠子移到個位上變成10顆珠子。(見圖3)

師：單位變小一級，數量就變多了，十位上的一個1就是個位上的10個1，接著怎么分？

生：移過來的10顆珠子和個位上原來的2顆珠子合起來共12顆珠子，平均分成2份，每份6顆。

師：講得真好，那么這一步在豎式上怎么表示？

生：個位上商6，2×6=12，12-12=0，沒有余數。(見圖4)

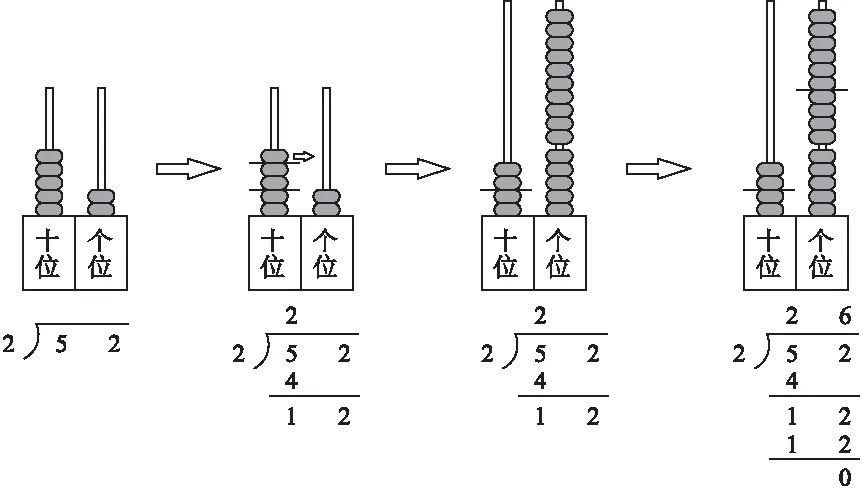
圖1 圖2 圖3 圖4

在教學中，我通過在計數器上分珠，將抽象的算理直觀化，借助計數器這一教具，引導學生將“分—換—合—再分”的操作過程與豎式除法運算中的“除—余—合—再除”的計算過程建立聯系，這樣學生就很容易明白算理。

算法是算理的語言表征，是對計算方法的語言概括。在教學中我有意識地將除法豎式寫在計數器下面，數位相對，讓學生感受到“除到哪一位，商就上在哪一位”。同時“巧”用計數器，打破計數器上每個數位上珠子數不能破十的限制，直觀呈現“上一位的‘1’換成下一位的‘10’”，凸顯了“計數單位轉換”這一核心，有效說明“如果有余數，要以‘1’當‘10’，和下一位上的數合起來再除”這一算法。

二、以計數器建聯系，形成數學思想

(一)建立豎式除法和口算除法的聯系

以下是我在教學中的一個教學片段：

師：同學們，比較這個算式的口算和豎式計算過程，你想說什么？

學生思考，討論。

師提示：我們要結合豎式除法過程中計數器的撥珠過程觀察。

生：口算和豎式計算的道理是一樣的。

教師及時給予肯定，根據學生的回答，結合計算器完成以下總結(見圖5)：

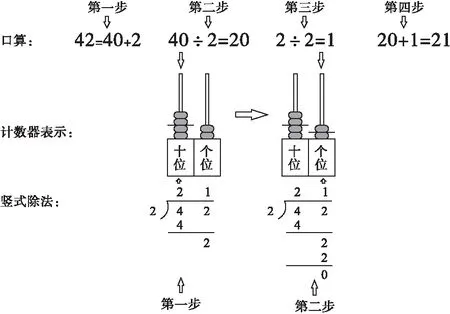
圖5

不難看出，用計數器作媒介，學生很容易看出口算除法和豎式除法雖表達形式完全不一樣，但實質上都是先將被除數按數位進行拆分，再分別進行平均分。

(二)建立豎式除法和豎式乘法的聯系

教學片段如下：

師課件出示練習：根據下圖計數器所表示的含義寫一道豎式乘法和一道豎式除法。(見圖6)

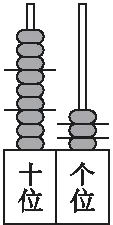
圖6

學生練習，討論。

請兩名同學分別上黑板寫豎式乘法和豎式除法,師生共同總結結果如下圖7：

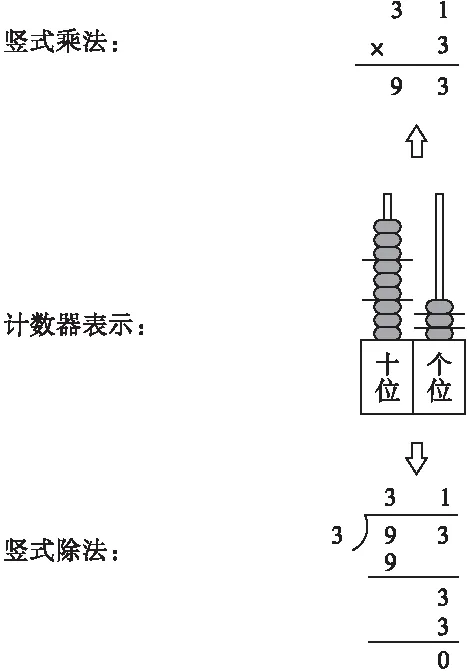
圖7

師：你發現了什么？

生：我發現同一幅計數器示意圖所表示的豎式乘法和豎式除法是相互聯系的。它們是逆運算。

“聯系”是一種重要的數學思想，教學中，我充分利用計數器建立豎式除法和口算除法以及豎式乘法之間的聯系，有效滲透這一數學思想教育，深化學生對豎式除法的認知，讓學生體會到小學數學知識是一個整體。

三、用計數器巧破疑，使教學更深入

在教學中，我們要重視學生的疑問，因為學生的疑問往往是學生沒有弄懂的知識點，也是學生思維的生長點。

在課堂交流環節，有位喜歡動腦的學生問道:“老師，原先的豎式計算都是從低位算起，為什么豎式除法非要從高位算起？”此問一出，學生們都小聲議論起來。看來這個問題引起大家的共鳴，我要抓住這個契機進行深度教學，接著進行了以下教學。

教學片段如下：

師：前面我們計算42÷2=和52÷2=時都是從高位算起，現在請同學們利用計數器探究一下，它們能從低位算起嗎？

學生探究，在本子上畫計數器演示圖和相應的豎式除法計算過程，師巡視并指導。

學生匯報：

生1出示42÷2=的計數器演示圖及相應的除法豎式。

生1：我覺得42÷2=可以從低位算起。

師：請你告訴大家為什么？

生1：先分個位上的2顆珠子，除以2，每份是1顆，正好分完，在個位上商1；再分十位上的4顆珠子，除以2，每份是2顆，正好分完，在十位上商2。合起來商為21。

師表揚，提高語氣道：“那豎式除法可以從低位除起嗎？”

生2：不能，我覺得52÷2=不能從低位除起。

師：請你來告訴大家為什么。

生2出示52÷2=的計數器演示圖及相應的除法豎式。

生2：從個位算起，個位上2顆珠子，除以2，每份1顆珠子，這一步沒有問題，但接下來算十位時，十位上的5顆珠子除以2，每份2顆，還余1顆，不能除盡，這余下的1顆珠子我又把它移到個位上，換成個位上的10顆珠子，進行二次平均分，這樣計算太麻煩了，還容易算錯，沒有從高位算起來簡便。

師鼓掌，道：同學們，現在你們覺得豎式除法是“從高位算起”好呢，還是“從低位算起”好呢？

生3：“從高位算起”好。

師：請你說說理由。

生3：因為“從低位算起”對于有的除法算式可行，有的不行；而“從高位算起”則對于任何除法算式都可行。

師：我也贊成這位同學的觀點，豎式除法是一種計算方法，作為一種計算方法，我們就要選擇最優算法，所以我們選擇“從高位算起”。

以上教學中，教師引導學生利用計數器進行自主探究，在探索中思考，在思索中感悟，解決了疑問。學生的學習由此引向深入，思維得到延伸，真正的學習自然而然發生。

總之，由于計數器的引入，豎式除法的課堂教學令人耳目一新，走出了計算教學常有的說教模式，不僅變得生動活潑，更增加了課堂教學的寬度和深度。在這里，計數器不僅能直觀形象地表征豎式除法的算理，表達算法，還是溝通數學知識豎向及橫向間聯系的有效手段和工具。它已成為學生深度思維的載體——以“計數器模型”來解決數學問題，成為學生思考數學問題的一種思維方式。