注重方法比較 善于變式拓展
——以一道向量模擬題的深度探究為例

貴州 李 寒

(作者單位：貴州省貴陽(yáng)市第一中學(xué))

向量是近代數(shù)學(xué)中重要和基本的概念之一，有著豐富的幾何背景，是解決幾何問(wèn)題的有力工具.它具有幾何形式和代數(shù)形式的“雙重身份”，能將數(shù)形融于一體，能與中學(xué)數(shù)學(xué)教學(xué)內(nèi)容的許多主干知識(shí)綜合，形成知識(shí)交匯點(diǎn)，成為“在知識(shí)網(wǎng)絡(luò)交匯處設(shè)計(jì)試題”的良好載體.下面對(duì)一道向量線性運(yùn)算與基本不等式交匯問(wèn)題的解法進(jìn)行探究，以體會(huì)方法優(yōu)化的重要性，通過(guò)對(duì)問(wèn)題的變式擴(kuò)展，以揭示這類(lèi)問(wèn)題的本質(zhì)和規(guī)律.

一、試題呈現(xiàn)

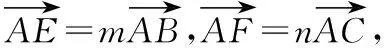
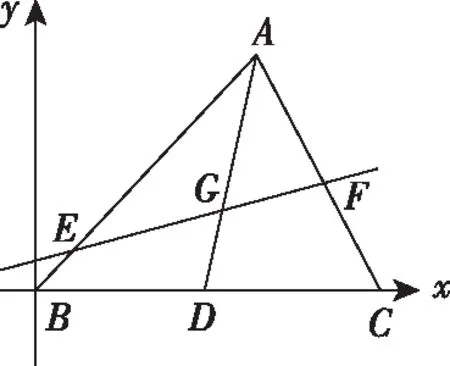
該題是平面向量與基本不等式應(yīng)用相結(jié)合的一道填空壓軸題，將直線過(guò)重心G轉(zhuǎn)化為向量表示，再結(jié)合已知的向量關(guān)系，推導(dǎo)出關(guān)于m，n的式子，最后利用基本不等式求解得到答案.

二、解題探究

1.解法賞析

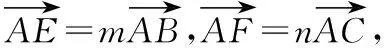
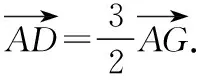
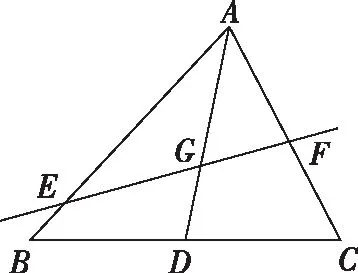
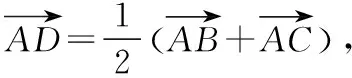
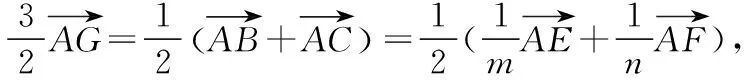
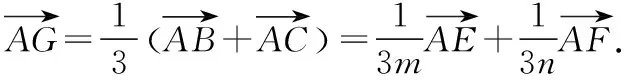
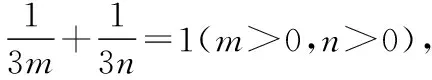
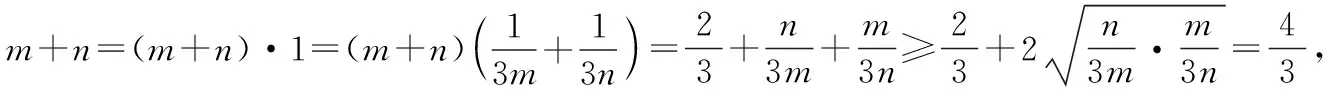
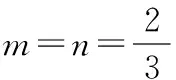
解法2(向量坐標(biāo)法)：連接AG并作AG的延長(zhǎng)線交BC于點(diǎn)D.

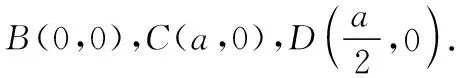
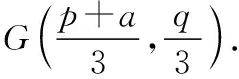
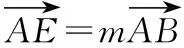
所以x1=(1-m)p，y1=(1-m)q，所以E((1-m)p，(1-m)q).

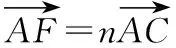
所以x2=na+(1-n)p，y2=(1-n)q，所以F(na+(1-n)p，(1-n)q).

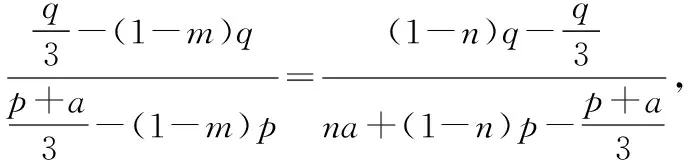
點(diǎn)評(píng)：解法2通過(guò)建立直角坐標(biāo)系，將問(wèn)題用向量坐標(biāo)表示，通過(guò)向量的坐標(biāo)運(yùn)算，使問(wèn)題程序化，其目標(biāo)明確，思路清晰，思維難度小，但向量坐標(biāo)法的運(yùn)算量較大，對(duì)數(shù)學(xué)運(yùn)算核心素養(yǎng)要求較高.

解法3(幾何法)：如圖，連接AG并作AG的延長(zhǎng)線交BC于點(diǎn)D.

因?yàn)辄c(diǎn)G是△ABC的重心，所以點(diǎn)D是BC的中點(diǎn)，即BD=DC.

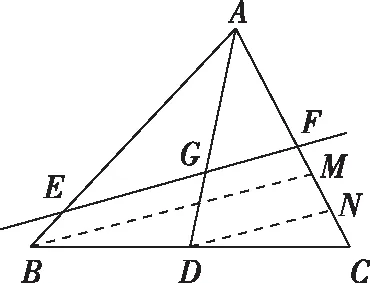
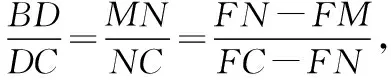
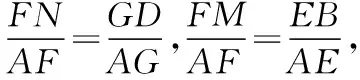
點(diǎn)評(píng)：解法3利用了平行線分線段成比例定理，得到線段的比例關(guān)系后，將已知條件的向量關(guān)系轉(zhuǎn)化為線段長(zhǎng)的比例關(guān)系求解.幾何法別出心裁，過(guò)程簡(jiǎn)潔、條理清晰，對(duì)邏輯推理核心素養(yǎng)要求較高.

2.方法比較

向量所具有的“數(shù)”與“形”的雙重特征，為數(shù)形結(jié)合提供了良好的載體.求解向量有關(guān)問(wèn)題通常有兩種思路：一是“形化”，即從向量基底法的角度思考，基底法是解決向量問(wèn)題的通性通法；二是“數(shù)化”，即從坐標(biāo)法的角度思考，坐標(biāo)法是解決向量問(wèn)題的常用方法.根據(jù)上述給出的三種方法，比較得到如下結(jié)論：

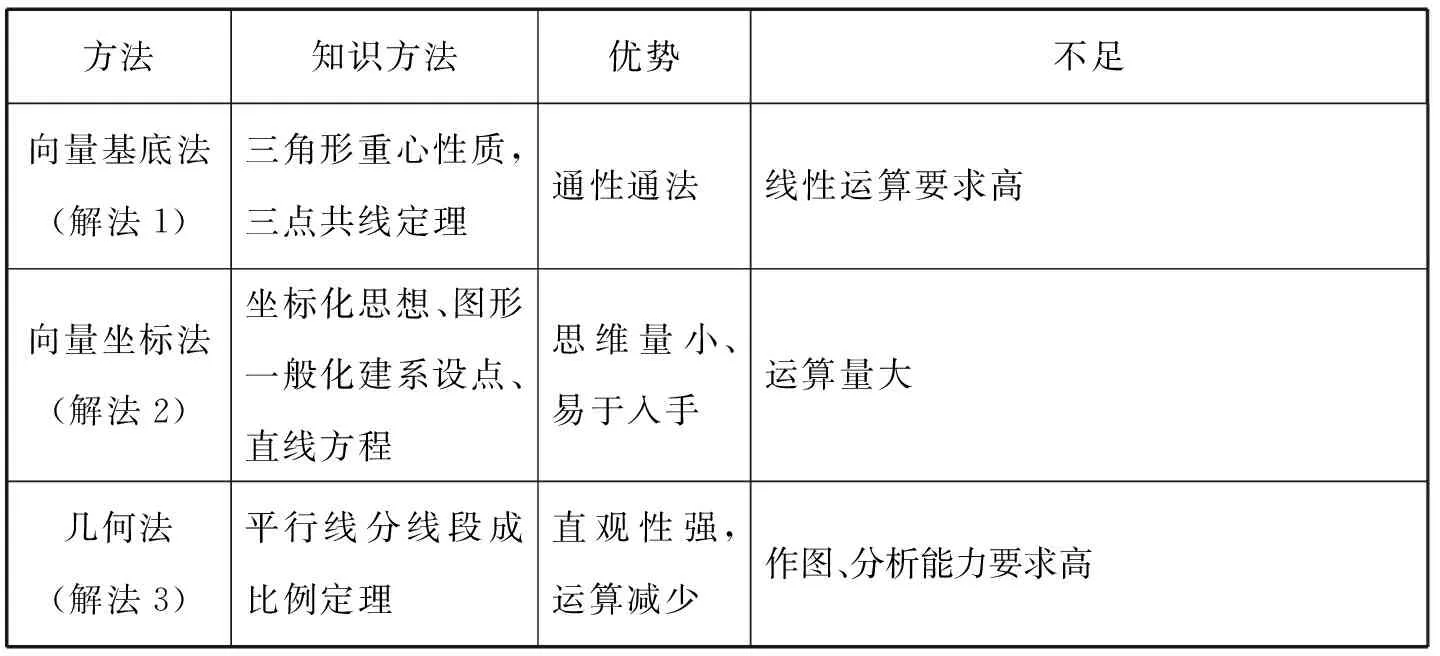
方法知識(shí)方法優(yōu)勢(shì)不足向量基底法(解法1)三角形重心性質(zhì),三點(diǎn)共線定理通性通法線性運(yùn)算要求高向量坐標(biāo)法(解法2)坐標(biāo)化思想、圖形一般化建系設(shè)點(diǎn)、直線方程思維量小、易于入手運(yùn)算量大幾何法(解法3)平行線分線段成比例定理直觀性強(qiáng),運(yùn)算減少作圖、分析能力要求高

上述思路方法體現(xiàn)的均是中學(xué)數(shù)學(xué)解題的思想和方法.雖然在高考復(fù)習(xí)備考的臨考階段時(shí)間緊、任務(wù)重，但對(duì)典型試題的解答要主動(dòng)歸納總結(jié)各種不同的方法，并熟練掌握處理問(wèn)題的通性通法，在掌握基本方法的同時(shí)，要學(xué)會(huì)分析、比較、優(yōu)化解題方法，唯有如此，當(dāng)學(xué)生遇到不同問(wèn)題時(shí)，才會(huì)選擇恰當(dāng)?shù)姆椒ǎ忸}時(shí)少走彎路.

3.延伸結(jié)論

上面解題過(guò)程中，其實(shí)蘊(yùn)含著直線過(guò)三角形重心的一個(gè)充要條件的結(jié)論，即

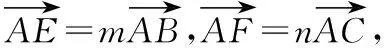
三、變式探究

探究1：若上述問(wèn)題中直線EF不過(guò)重心G，會(huì)有怎樣的關(guān)系呢？探究如下：

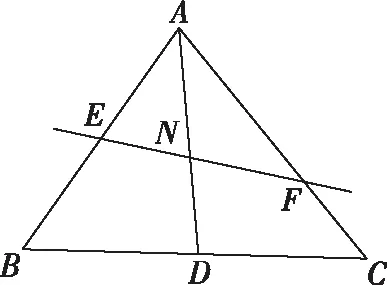
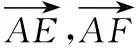
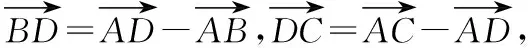
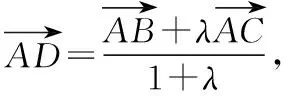
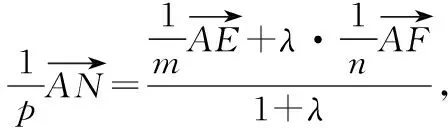
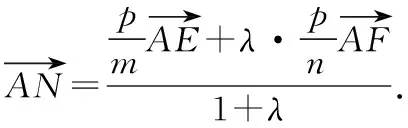
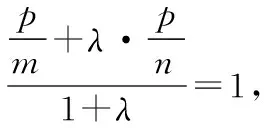
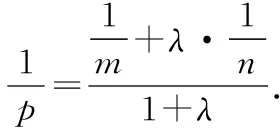
其實(shí)，若將變式1中向量關(guān)系做一下變動(dòng)，可得到：

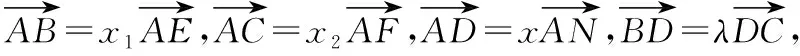
若進(jìn)一步將向量關(guān)系變?yōu)榫€段比值關(guān)系，可得到：

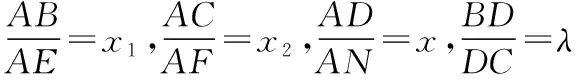
根據(jù)推論1，也可以得到：

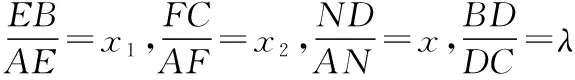
推論1、2將三角形中的某些線段的長(zhǎng)度之比統(tǒng)一到一個(gè)公式中，其結(jié)構(gòu)、形式與解析幾何中的定比分點(diǎn)坐標(biāo)公式一致，簡(jiǎn)潔、整齊、易記，故稱為幾何“分點(diǎn)坐標(biāo)公式”，利用該定理可以解決平面幾何中，三角形被直線所截得的線段比的一類(lèi)問(wèn)題.

探究2：若將變式1研究的方向改為求向量的數(shù)量積，又會(huì)是怎樣的情形呢？探究如下：

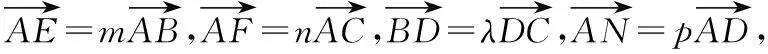
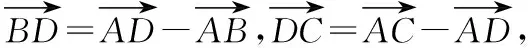
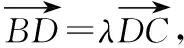
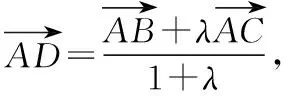
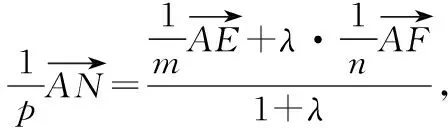
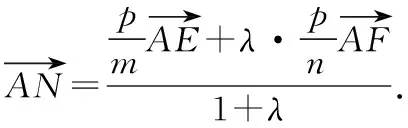
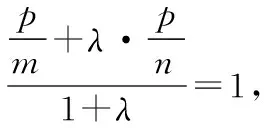
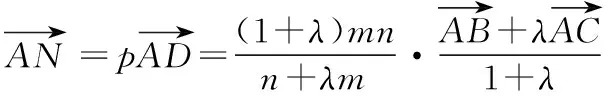
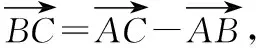
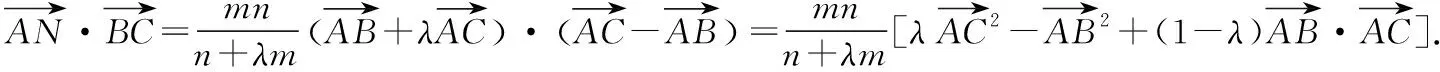
由此，我們可以得到一般性結(jié)論：

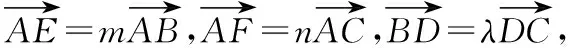
特別地，若D為△ABC的BC邊的中點(diǎn)，即λ=1，則有：

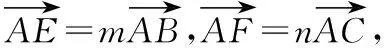
相比較而言，命題2的推論具有更廣泛的應(yīng)用.

四、應(yīng)用舉例

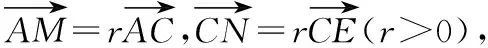
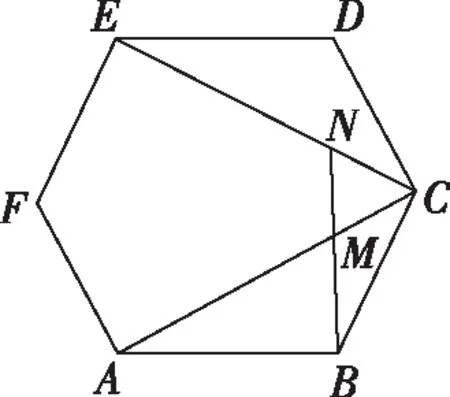
解析：如圖，連接BE交AC于點(diǎn)H，設(shè)正六邊形ABCDEF的邊長(zhǎng)為1，則由正六邊形的性質(zhì)可得BE=2.

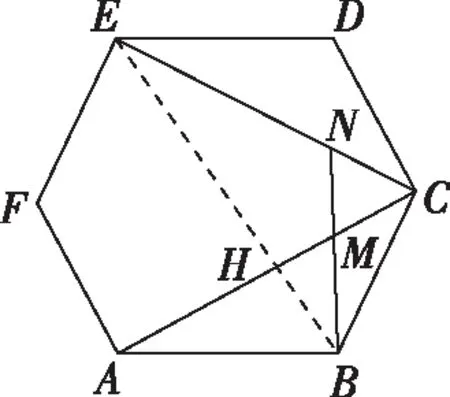
在Rt△CHB中，因?yàn)椤螧CA=30°，

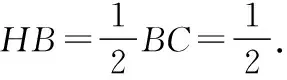
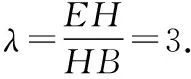
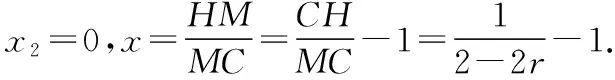
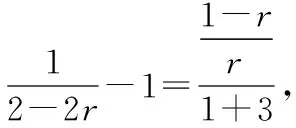
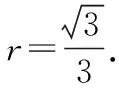
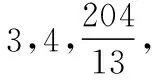
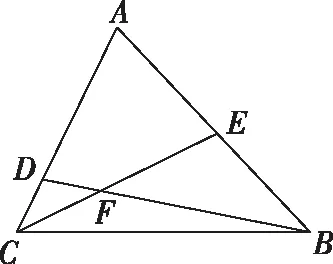
解析：設(shè)△BCF的面積為S，

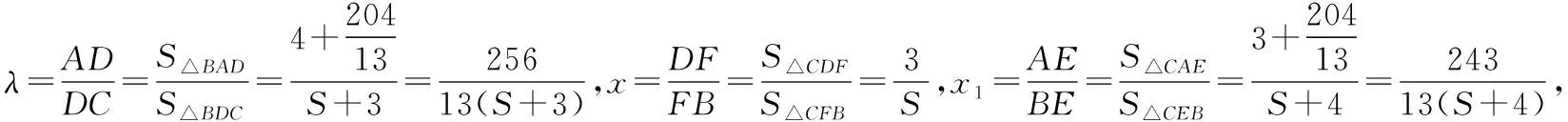
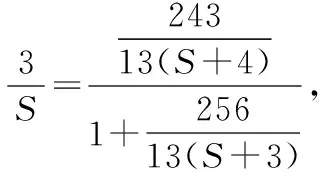
整理得17S2-26S-295=0，

所以(S-5)(17S+59)=0，

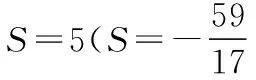
故△BCF的面積為5.

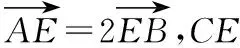
A.-6B.-3

C.3 D.6

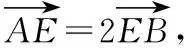
五、教學(xué)啟示

在高考復(fù)習(xí)備考的臨考沖刺階段，想要打造精準(zhǔn)、高效的教學(xué)課堂，需要從根本上改變教與學(xué)的方式，發(fā)展學(xué)生解決問(wèn)題的意識(shí)和能力.數(shù)學(xué)解題是鞏固基礎(chǔ)知識(shí)、落實(shí)基本技能、感悟思想方法、提升思維敏銳度的系統(tǒng)活動(dòng)，數(shù)學(xué)教學(xué)研究的過(guò)程主要就是解決問(wèn)題的過(guò)程，掌握數(shù)學(xué)知識(shí)的一個(gè)重要標(biāo)志就是善于解題.特別是在講評(píng)課中，對(duì)典型問(wèn)題的一題多解、同型歸類(lèi)是不錯(cuò)的選擇.與此同時(shí)，要從已經(jīng)解決的問(wèn)題入手，對(duì)問(wèn)題延伸、挖掘，進(jìn)行變式探究，尋找到處理此類(lèi)問(wèn)題有效的規(guī)律和方法，培養(yǎng)學(xué)生的探究意識(shí)和解題能力.總之，對(duì)典型試題適宜地進(jìn)行對(duì)解法、變式及拓展等方面的教學(xué)與訓(xùn)練，既能梳理解決這類(lèi)問(wèn)題的一般方法，尋求解答此類(lèi)問(wèn)題的通性通法，揭示問(wèn)題的本質(zhì)和一般規(guī)律，又能拓寬學(xué)生的知識(shí)面，權(quán)衡解法優(yōu)劣，積累解題經(jīng)驗(yàn)，讓學(xué)生走出“題海”，提高復(fù)習(xí)時(shí)的解題效率，力爭(zhēng)在2022年高考中取得優(yōu)異的成績(jī).