追本溯源 高瞻遠矚
——立體幾何中的動態問題研究

浙江

(作者單位：浙江省柯橋中學)

立體幾何中的動態問題，其核心考點是動點和動直線所構成的靜態平面，難點是考查學生數學核心素養和創新思維能力，已成為新高考命題的一大熱點.深挖其問題背景，總結其求解方法，掌握其證明技巧，透析其變化規律，對提升考生的數學復習效益將大有裨益.

一、真題研學

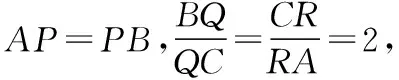
A.γ<α<βB.α<γ<β

C.α<β<γD.β<γ<α

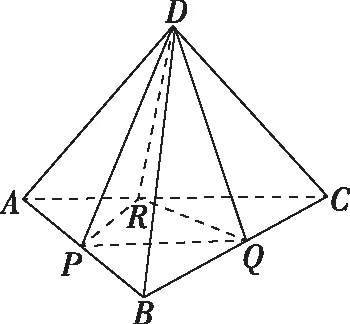
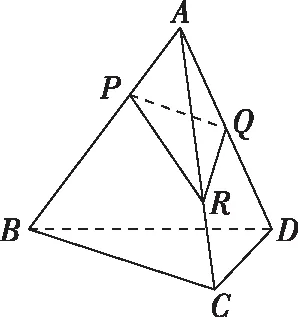
根據題意，過D作平面ABC的高DH，過H分別作PR,PQ,QR的高HE,HF,HG，如圖，易得α=∠DEH，β=∠DFH，γ=∠DGH，可以看出它們的對邊都是一樣的，所以只需要比較EH,FH,GH三邊的大小即可，即把立體問題轉化為底面平面幾何問題.

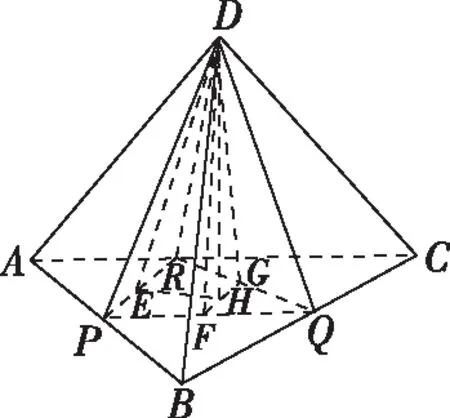
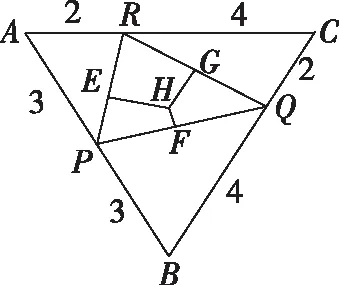
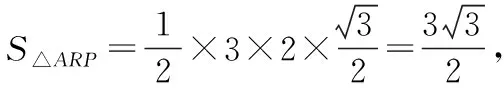
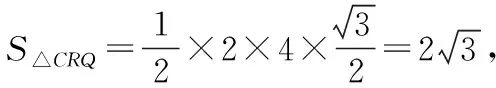
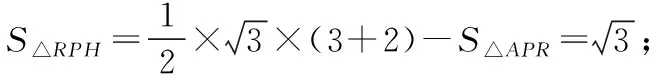
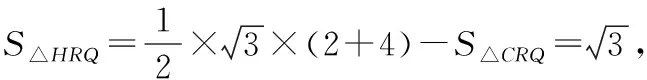
然后我們細究命題思路，該題是在取底面正三角形三邊中點的基本模型下，改為其中兩邊的近、遠三等分點，從而命制出一個立足課本基本模型的立體幾何好題，我們就以該真題為研究對象，將中點、三等分點改成任意棱上一點，編制出一道一模題如下.

二、好題細品

母題：如圖，三棱錐V-ABC的底面ABC是正三角形，側棱長均相等，P是棱VA上的點(不含端點)，記直線PB與直線AC所成角為α，二面角P-AC-B的平面角為β，則α+β不可能是( )

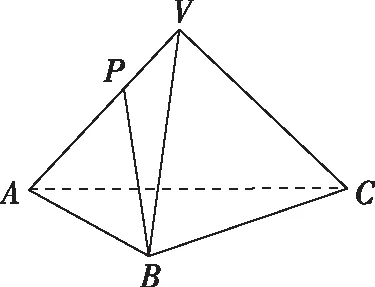
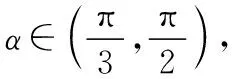
點評：該題是將極限思想運用到立體幾何中，將三棱錐趨向于無窮小及無窮大，則角的范圍迎刃而解.

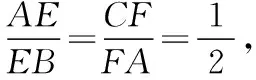
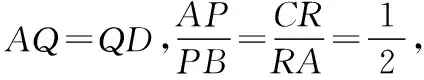
A.β>γ>αB.α>β>γ

C.α>γ>βD.β>α>γ

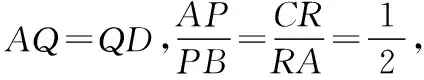
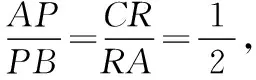
繼2017年之后，浙江卷2018，2019兩年連續考到了動態空間三角的大小比較關系，通法是通過線面垂直關系先做出線線、線面、二面角，把立體幾何問題最終轉化為一個簡單平面問題，再比較線段長大小.當然空間三角大小關系也隱含著最小角，最大角定理的運用.

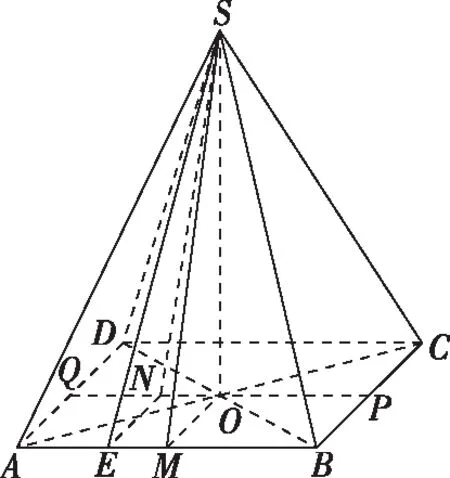
(2018·浙江卷·8)已知四棱錐S-ABCD的底面是正方形，側棱長均相等，E是線段AB上的點(不含端點),設SE與BC所成的角為θ1，SE與平面ABCD所成的角為θ2，二面角S-AB-C的平面角為θ3，則( )

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

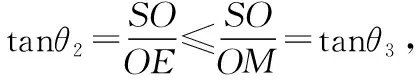
(2019·浙江卷·8)設三棱錐V-ABC的底面是正三角形，側棱長均相等，P是棱VA上的點(不含端點).記直線PB與直線AC所成的角為α，直線PB與平面ABC所成的角為β，二面角P-AC-B的平面角為γ，則( )

A.β<γ，α<γB.β<α，β<γ

C.β<α，γ<αD.α<β，γ<β

2019年高考的動態立體幾何仍延續2018年的最小角、最大角定理，故易選B.

然后我們將模型由三棱錐換成標準正交勻稱圖形正方體，設置一個由動點連接定點的隱平面，即得到以下題目.

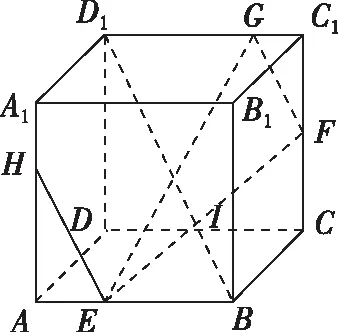
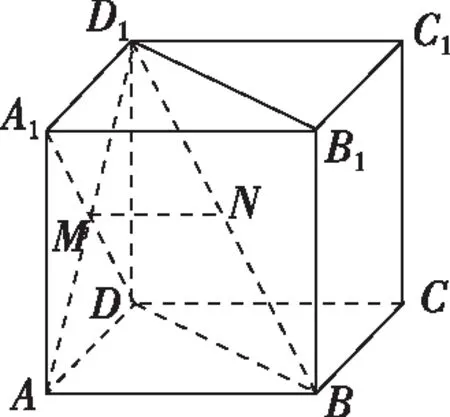
【變式2】(2021·寧波一模·16)在正方體ABCD-A1B1C1D1中，E為線段AB上任意一點(不含端點)，F為CC1的中點，G為C1D1的四等分點(靠近點C1)，直線AA1交平面EFG于點H，則直線EH與直線BD1所成角的余弦值是________.

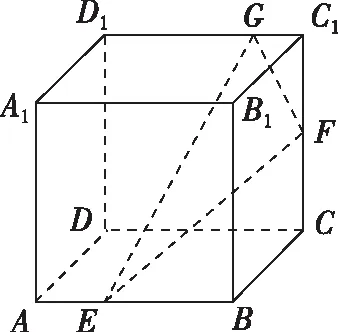
該題雖E為動態點，而事實上平面ABB1A1∥平面DCC1D1，平面EFG為截面，過E作EH∥FG交AA1于點H，平面EFG與平面ABB1A1和平面DCC1D1截得的兩直線EH∥FG，從而直線EH與直線BD1所成角等于直線FG與直線BD1所成角.以下可使用向量的對角線定理

關于平面的延拓性是共面的難點，該知識點在2021年浙江卷第6題進行了考查.

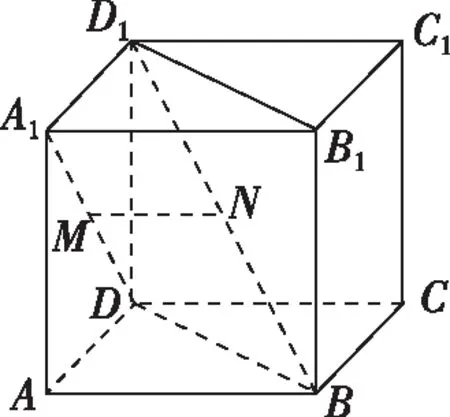
如圖，已知正方體ABCD-A1B1C1D1，M，N分別是A1D，D1B的中點，則( )

A.直線A1D與直線D1B垂直，直線MN∥平面ABCD

B.直線A1D與直線D1B平行，直線MN⊥平面BDD1B1

C.直線A1D與直線D1B相交，直線MN∥平面ABCD

D.直線A1D與直線D1B異面，直線MN⊥平面BDD1B1

需要將D1B固定到平面ABD1，連接AD1，由正方體可知A1D⊥AD1，A1D⊥AB，所以A1D⊥平面ABD1，A1D⊥D1B，易得MN∥AB，MN∥平面ABCD.所以A選項正確；由正方體可知A1D與平面BDD1相交于點D，D1B?平面BDD1，D?D1B，直線A1D與直線D1B是異面直線，B，C錯；因為MN∥AB，AB不與平面BDD1B1垂直，所以MN不與平面BDD1B1垂直，故D錯，故選A.

通過以上三例我們闡述的是立體圖形中的動點，動直線運動規律，而在新普通高中教科書數學必修第二冊中，明確告訴我們什么是立體幾何，立體幾何是在平面幾何的基礎上構成的正交或是仿射維度圖形，其本質是基于點射影的解析幾何.鑒于此，2022年高考動態立體幾何試題命制將青睞于平面幾何的折疊，依照母題的三棱錐，改編成平面圖形為三角形的翻折問題，得到變式3.

三、2022年真題預測

【變式3】如圖，已知△ABC中，AC>AB,AD是∠BAC的平分線，將△ABD沿直線AD翻折成△ADB1,在翻折過程中，設所成二面角的平面角B1-AD-C為α，∠B1AC=β,∠B1DC=γ,則下列結論中成立的是( )

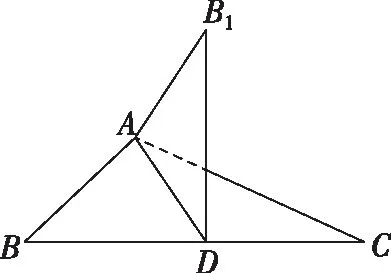
A.α≥β,α≥γB.α≥β,α≤γ

C.α≤β,α≥γD.α≤β,α≤γ

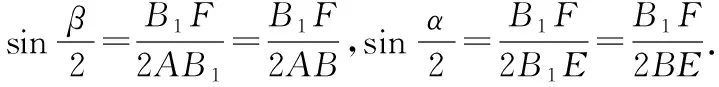
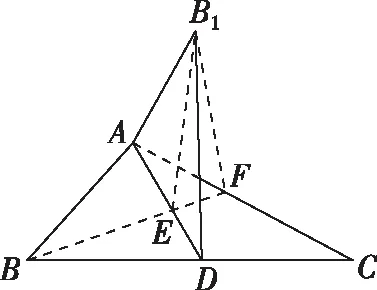
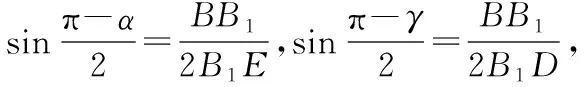
點評：立體幾何翻折問題常先考慮折疊前圖形與折疊過程中的圖形的變量與不變量，也是極端法的緣由，其次該題解法的紐帶是投影點B′一定落在AD的高線上.

當然在考場上，我們可以再次引入點的極限逼近思想，考慮兩個極端位置，在初始位置，易知α=π,α>β,α=γ,其次在點B經過180°折平時易知α=β=0,α<γ，易得準確答案B，讓我們再次感嘆動態逼近思想的精妙絕倫.

此外我們也可以把基本圖形改為直角三角形，在折疊過程中構成標準垂直的立體點正投影，得到試題變式4.

【變式4】在△ABC中，∠ACB=90°,BC=2,AC=3，點D在斜邊AB上，以CD為棱把它折成直二面角A-CD-B，折疊后AB的最小值為( )

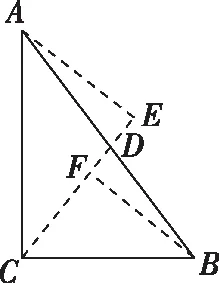
因為折成直二面角A-CD-B，為標準正投影，故點A的投影必在直線CF上，該題本質是兩個直角三角形的標準墻角模型.簡單計算下可設∠ACE=θ,AE=3sinθ,CE=3cosθ,CF=2sinθ,BF=2cosθ，所以AB2=13-6sin2θ≥7，故選B.變式3與變式4是筆者對2022年高考動態立體幾何的預測.

四、結束語

《普通高中數學課程標準(2017版2020年修訂)》指出“高中數學教學以發展學生數學學科核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質”.本文闡述的立體幾何動態問題研究正是落實這一理念的良好載體.在解決此類題型時，教師要以高考真題為核心，從學生的角度去思考問題，從條件或是結論或是模型的演變為導向得到變式題型，由淺入深，由易到難，由特殊到一般，層層深入，步步啟發.精心設計的變式題組在教學中發揮著不可替代的作用，對于提高教學效率、培養尖子生的能力、提高學生的數學素養起著重要作用，筆者鑒于此與各位讀者共勉，希望能不斷優化課堂教學，研討出更多值得品味的優質試題.