基于直觀想象的立體幾何試題命制探究

福建 林清利 唐碧容

(作者單位：福建省莆田第一中學)

2020-2021年的高考試題全面考查了高中數學六大核心素養，作為一線教師應當充分挖掘高考試題的內涵，領會核心素養導向，并潛心探索如何在平時的課堂中加以落實.直觀想象是六大核心素養之一，它是指借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形，理解和解決數學問題的素養.通過直觀想象，可以預判問題的發展方向，站在更高的角度俯瞰題目，抓住問題的核心，命制萬變不離其宗的試題.

本文通過一道高考真題的變式研究及溯源，以一題多解、一題多變、回歸教材等方式研究問題本質.先用解析法探究，然后著重用幾何法分析，通過直觀想象感知空間中的線面角、二面角的作圖方法，減少計算量，提高抽象思維的要求.闡明變式過程中的“變”與“不變”，抓住變式規律和方向，形成命題式的教學模式，并以“微專題”的形式在平時教學中加以實踐.

1.經典母題

【例】(2021·全國甲卷理·19)已知直三棱柱ABC-A1B1C1中，側面AA1B1B為正方形，AB=BC=2，E，F分別為AC和CC1的中點，D為棱A1B1上的點，BF⊥A1B1.

(1)證明：BF⊥DE；(2)當B1D為何值時，平面BB1C1C與平面DFE所成的二面角的正弦值最小？

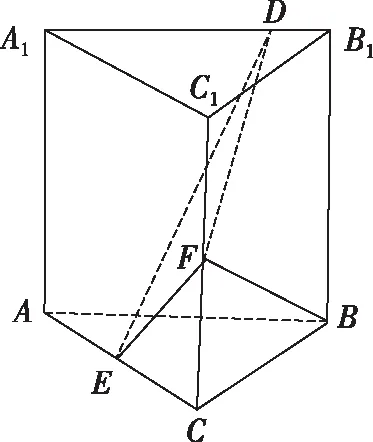
分析：本題的幾何體是直三棱柱,這給考生直觀的視覺感知.題干中第二個條件蘊含垂直,結合最后一個條件,先直觀預判BA,BC,BB1兩兩垂直,然后借助長度關系加以證明，這堅定了考生建立直角坐標系來解題的自信.

雖然D是動點,造成兩個問題中均含有動態的直線或平面的空間角的問題,但是命題人把動點D控制在直線A1B1上,使用坐標法可以簡潔輕松地完成本題兩問,一氣呵成.

2.解題探究

若僅滿足于坐標法解題,便缺少對本題命制手法的探究.基于直觀想象的幾何法無疑是探究本題的最佳視角,下面探究本題的特點、解法、題源及變式.

第(1)問分析1:注意到DE始終在△A1B1E內,故只需證明BF⊥平面A1B1E.

第(1)問分析2:考慮到BF是在“豎直”的平面B1BCC1內,而DE不在平面B1BCC1內,故只需證明DE在平面B1BCC1的投影與BF垂直即可.

第(2)問圖中沒有平面BB1C1C與平面DFE的公共棱,故應先把平面DFE延展,進而作出公共棱.

解答：(1)略；(2)如圖1,延長EF,A1C1,設EF∩A1C1=G,連接DG,設DG∩B1C1=H,連接FH.

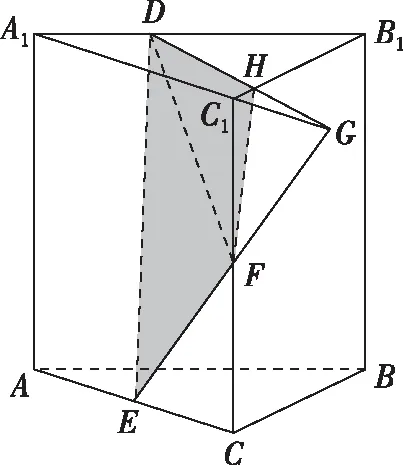
圖1

思路一:從點D出發作平面角.

解法一：如圖2,過B1作B1J⊥FH,垂足為J,連接DJ.由(1)知A1B1⊥平面B1BCC1,則A1B1⊥FH,且A1B1∩B1J=B1,從而FH⊥平面B1DJ,那么DJ⊥FH,所以∠B1JD是二面角D-FH-B1的平面角.

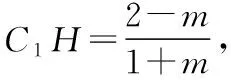
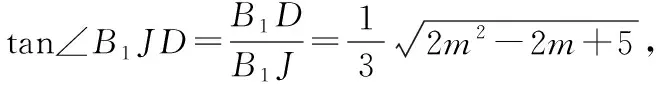
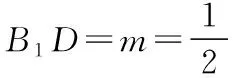
此時sin∠B1JD也最小.

圖2

思路二:從點E出發作平面角.

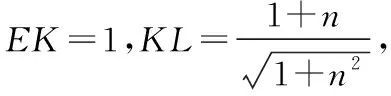
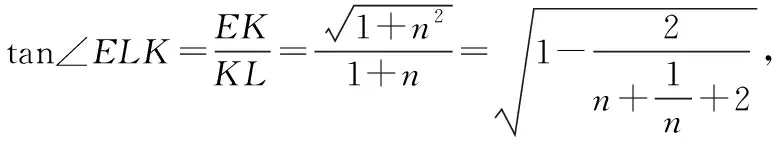
那么當C1H=n=1時tan∠ELK最小,

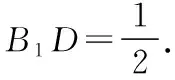
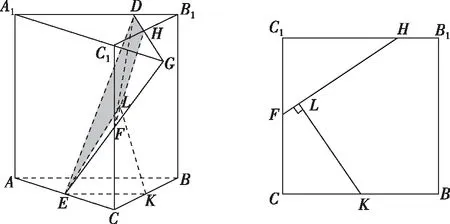
圖3

思路三:注意到△DEF在平面B1BCC1內的投影是確定的三角形,故無需作出公共棱和平面角.

解法三：如圖4,設BC中點為K,連接EK,KB1,B1F,FK,易證EK⊥平面B1BCC1,則△DEF在平面BB1C1C內的投影為△B1FK.設所求角為θ,△DEF與△B1FK的面積分別記為S△DEF,S△B1FK,

則S△B1FK=S△DEF·cosθ,由于EF,S△B1FK為定值,故當cosθ最大時,S△DEF最小,

從而點D到直線EF的距離最小,其最小值為異面直線A1B1與EF之間的距離d.

又由于A1B1∥平面EFK,那么d等于A1B1到平面EFK的距離,

即d等于B1到平面EFK的距離,亦即d等于B1到FK的距離.

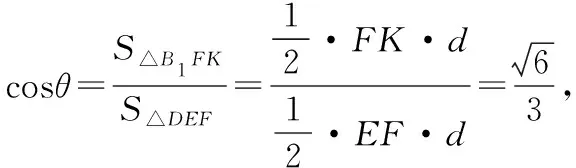
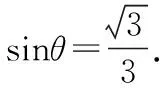
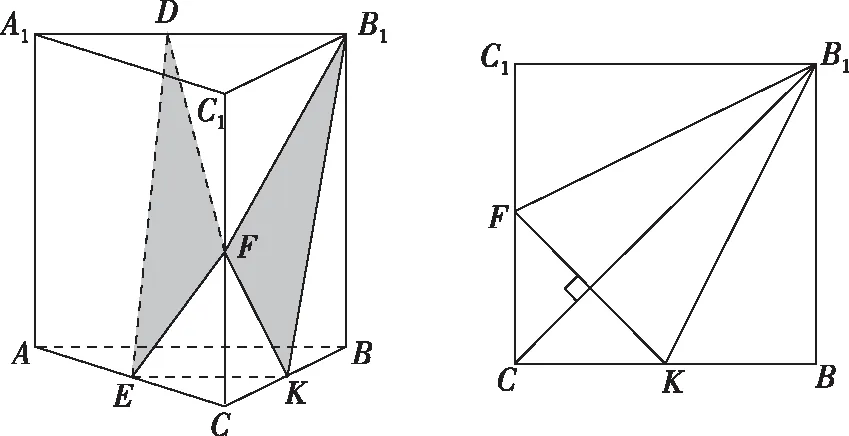
圖4

如圖5,連接B1C,CA1,設EF∩A1C=M,易知點M是線段A1C的三等分點(靠近C)，

又EF⊥B1C,A1B1⊥B1C,那么當DM∥B1C時,DM為異面直線A1B1與EF的公垂線.

從而點D是線段A1B1的三等分點(靠近B1),

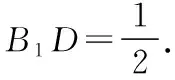
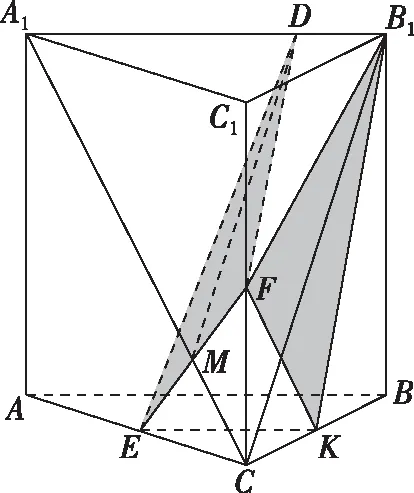
圖5

以上三種解法雖然都是幾何法,但是在計算量、思維量上有較大差別.解法一中由于D是動點,導致△B1DJ三邊均是變化的,計算量大;解法二中E是定點,Rt△ELK的一條直角邊是固定的,從而在計算量上得到了較大的精簡;解法三站在結論的基礎上看問題,并不斷地轉化問題,幾乎沒有運算量,把動態問題“動中求靜”的思路發揮得淋漓盡致,直擊問題本質.

3.變式拓展

母題變式1：尺規作圖問題在全國卷考題中也經常涉及,特別截面問題是熱點、難點問題.本題中△DEF在幾何體內部,故可在本題中增加一問：“請作出平面DFE截三棱柱ABC-A1B1C1的截面.”

解：延長EF,A1C1,設EF∩A1C1=G,連接DG,設DG∩B1C1=H,連接FH,則四邊形DEFH為所求截面.

母題變式2：由解法二發現點H完全由點D控制,且平面BB1C1C與平面DFE所成二面角的正弦值最小時,點H恰為線段B1C1中點,故本題可以改編為“H為棱B1C1上的點,當平面BB1C1C與平面EFH所成二面角的正弦值最小時,請確定點H的位置.(其他條件不變)”這樣設計從結果上看是中點,數據更直觀,更具有對稱美.

簡解：由上面的解法二可知當H為B1C1中點時,所求二面角的正弦值最小.

母題變式3：改變目標函數,例如求DE與面BB1C1C所成角的正弦值的取值范圍.

簡解：作DE在平面BB1C1C內的投影為B1K,DE與平面BB1C1C所成角α,則0≤α≤∠EB1K,

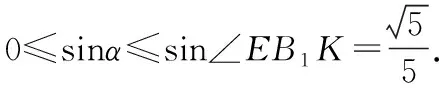
4.題源探究

1.如圖,兩條異面直線a,b所成角為θ,在直線a,b上分別取點A′,E和A,F,使AA′⊥a,且AA′⊥b,已知A′E=m,AF=n,EF=l,求線段AA′的長.

2.(2013·北京卷理·14)如圖，在棱長為2的正方體ABCD-A1B1C1D1中，E為BC的中點，點P在線段D1E上，點P到直線CC1的距離的最小值為________.

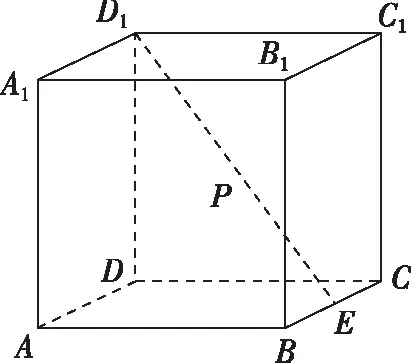
評注：以上兩題實質是探究兩條異面直線間的距離.雖然教材中不提這個概念,但是仍然作為習題探究.而且一些考題中會蘊含該模型,值得關注.

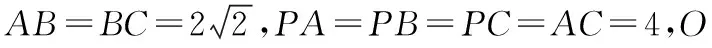
(1)證明：PO⊥平面ABC；

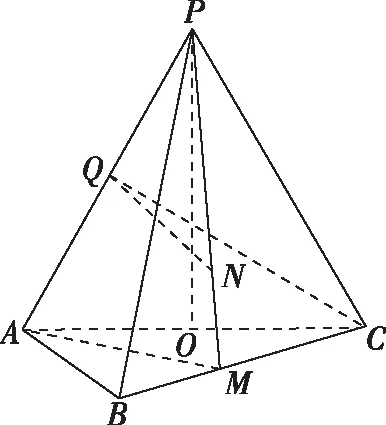
(2)若點M在棱BC上，且二面角M-PA-C為30°，求PC與平面PAM所成角的正弦值.

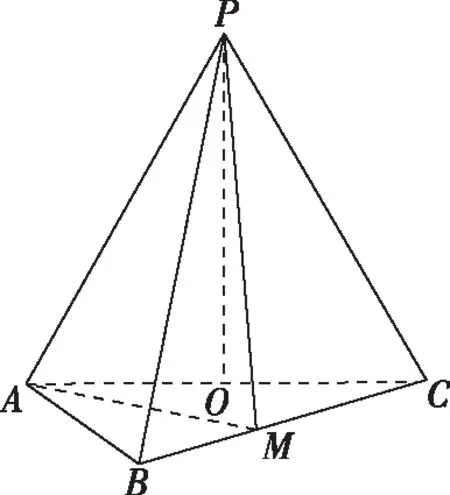
分析：第(2)問注意到二面角M-PA-C的一個半平面和所求問題中的平面PAM是公共的,而直線PC恰在另一個半平面內,從而本題非常適合從定義出發,借助投影,運用幾何法可以避開求解點M的坐標,也無需確定點M的準確位置,從而快速破解.

解：(1)略;(2)設AP中點為Q,連接CQ,則CQ⊥AP,作QN⊥AP交PM于N,則∠CQN=30°,

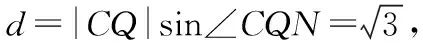
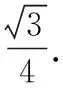
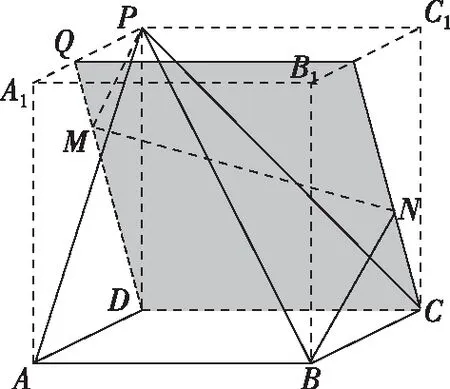
4.(2020·新高考Ⅰ卷·20)如圖，四棱錐P-ABCD的底面為正方形,PD⊥底面ABCD.設平面PAD與平面PBC的交線為l.

(1)證明：l⊥平面PDC；

(2)已知PD=AD=1，Q為l上的點,求PB與平面QCD所成角的正弦值的最大值.

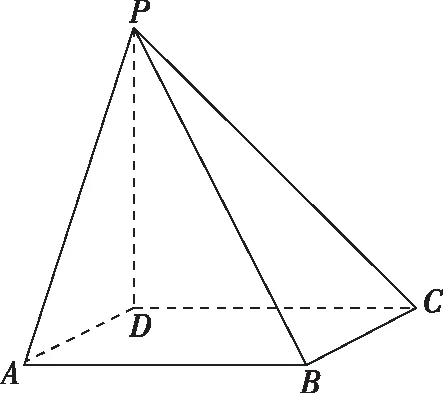
分析：由條件可知DA,DC,DP兩兩垂直且長度均相等,從而可以把幾何體補形為正方體,這樣直線PB在平面QCD的投影就比較直觀,從而可以快速破解.

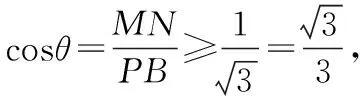
評注：以上兩道高考題以正方體為載體或有面面垂直等特殊條件,利用這樣的幾何直觀解題簡潔大氣,令人回味無窮,驚嘆模型的魅力,可以感受到全國卷命題專家的深厚功力.

5.總結規律

從上述考題的特點與解法中可以發現高考命題的一個基本理念是讓學生“多思少算”,那么要如何正確地思考,發散地思考呢?答案是基于核心素養的思考.利用幾何直觀,充分發揮想象,把解題與命題關聯起來,真正實現從解題到解決問題的升華.

對于立體幾何試題的解題與命制,對學生與教師的建議如下:

1.對于學生

(1)重視基本概念.概念是一切問題的基礎,數學玩得就是一個概念.學生在學習與復習的過程中要高度重視教材中關于概念的生成、理解和應用；

(2)重視基本方法.立體幾何中有坐標法與幾何法兩個基本方法.兩者要并重,特別是在解答題中,不能只會坐標法,適當地使用幾何法探究,將會收獲更多的思路與解法.

2.對于教師

(1)重視教材.一方面，鉆研教材,熟悉教材,才能整體把握知識的系統性.另一方面,高考試題的基本素材是教材.教材中的概念辨析,習題改編等都要高度重視；

(2)探究解法與變式.作為教師不能僅滿足坐標法,更需要熟悉幾何法.把問題歸類、模型化,探究其本源,進而把問題變式,實現多題一解,再嘗試命制一些試題,提升自身的綜合素質.

6.結束語

基于直觀想象的立體幾何試題的命制，首先要明確考查目標，然后尋找合適典型的模型載體，揭示問題本質，最后控制變量，明確問題中“變”與“不變”的關系,從解析法和幾何法的角度分別解釋“變”與“不變”.新高考試題正往兼具選拔和育人功能的良性方向不斷發展，作為一線教師，我們也要全力配合，我們的數學教學也應該是以育人為導向，課堂中要給學生發現問題、探究問題、討論問題、解決問題、改變問題的命題式數學學習體驗，提高他們直觀感知、預測、論證數學問題的能力.

(本文為福建省教育科學“十四五”規劃2021年度專項課題《核心素養視域下高考數學命題研究》研究成果之一(課題編號Fjjgzx21-006)