透過觀察 抓住本質
——巧解排列組合中的有序數(shù)組問題

魯和平

(浙江省嘉善第二高級中學,314100)

在高中數(shù)學排列組合問題教學中,學生有時會遇到一類有序數(shù)組問題.這類題目都有一個華麗的外表迷惑學生,需要我們用一雙慧眼由表及里、去偽存真,透過現(xiàn)象看本質,只有通過不斷轉化命題方能抓住問題最本質的內(nèi)核,使問題冰消獲解.

一、抽絲剝繭,始見真容

有些題目,單從外表來看,學生就已望洋興嘆.但如果我們冷靜分析,將所有已知條件進行轉化與化歸,就會有“驀然回首,那人卻在燈火闌珊處”的感覺.

例1設?ABC的內(nèi)角滿足A≤B≤C,且cos 20A=cos 20B=cos 20C=1,則滿足要求的數(shù)組(A,B,C)共有______個.

解由條件可知20A=2k1π,20B=2k2π,20C=2k3π,其中k1,k2,k3∈N*,k1≤k2≤k3.在?ABC中，由A+B+C=π,可得20(A+B+C)=2(k1+k2+k3)π=20π,即k1+k2+k3=10.

用枚舉可知(k1,k2,k3)=(1,1,8),(1,2,7),(1,3,6),(1,4,5),(2,2,6),(2,3,5),(2,4,4),(3,3,4),相應的(A,B,C)共有8個.

二、刪繁就簡,水落石出

有些題目條件紛繁無序,求解時往往要借力于多次的命題轉化,甚至要隨時借助函數(shù)的神力,才能撥開云霧見天日.

例2若正整數(shù)a,b,c,d滿足a+b=c+d,ac=bd,ad=bc,且20≤ab+bc+cd+da≤2 020,則滿足以上條件的有序數(shù)組(a,b,c,d)共有多少個?

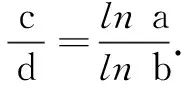
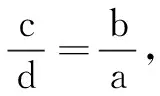
設f(x)=xlnx,則f(a)=f(b),又f(x)在(2,+∞)單調增,故a=b.又ac=bd,故c=d.再由a+b=c+d,可得a=b=c=d.結合20≤ab+bc+cd+da≤2 020,可得5≤a2≤505,故3≤a≤22,相應有序數(shù)組(a,b,c,d)共有20個.

若a=1或b=1,同理可得a=b=c=d=1,此時ab+bc+cd+da=4,與已知條件矛盾.

綜上,所求有序數(shù)組(a,b,c,d)共有20個.

三、快速鏈接,腦洞大開

如果我們大腦里儲存的數(shù)學知識容量大且結構佳,在審題時就能浮想聯(lián)翩,快速鏈接,慧眼識真金.

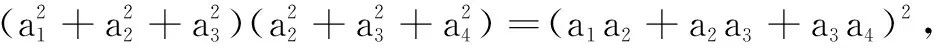
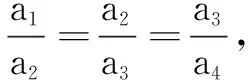
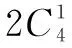
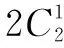
由加法原理,可知所求(a1,a2,a3,a4)共有38個.

四、條分縷析,思路井然

有些問題存在多種可能性,無法一言以蔽之.那就需要我們思維縝密,把各種可能性考慮周全,再按照一定標準進行分類討論,則可使思路既有條理又流暢清晰.

例4已知?ABC的……