利用阿基米德三角形的性質(zhì)求解面積問(wèn)題*

唐義恒 王安國(guó) 陳 亮

(重慶市合川中學(xué),401520) (重慶市合川區(qū)教育科學(xué)研究所,401520)

拋物線的弦與過(guò)弦的端點(diǎn)的兩條切線所圍成的三角形稱為阿基米德三角形,它具有許多有趣的性質(zhì).在近幾年的高考試題中,多次出現(xiàn)涉及阿基米德三角形的面積問(wèn)題.本文以拋物線x2=2py(p>0)為例,闡述如何利用阿基米德三角形的兩個(gè)基本性質(zhì)求解相應(yīng)問(wèn)題.

一、性質(zhì)與面積公式

性質(zhì)1阿基米德三角形底邊上的中線平行(或重合)于拋物線的對(duì)稱軸.

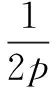
證明如圖1,設(shè)點(diǎn)A(x1,y1),B(x2,y2)在拋物線x2=2py(p>0)上,弦AB為阿基米德三角形的底邊,M為底邊AB的中點(diǎn),D為兩切線DA,DB的交點(diǎn).

易知過(guò)點(diǎn)A,B的切線方程分別為

x1x=p(y+y1),

①

x2x=p(y+y2).

②

下面利用該結(jié)論求解阿基米德三角形面積問(wèn)題.

二、真題解答

(1)證明:直線AB過(guò)定點(diǎn);

解(1)略.

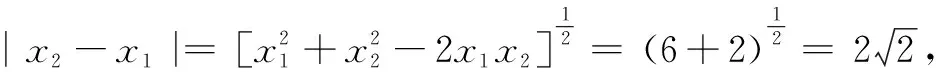
例2(2021年全國(guó)高考題)己知拋物線C:x2=2py(p>0)的焦點(diǎn)為F,且點(diǎn)F與圓M:x2+(y+4)2=1上點(diǎn)的距離的最小值為4.

(1)求p;

(2)若點(diǎn)P在圓M上,PA,PB是C的兩條切線,A,B是切點(diǎn),求?PAB面積的最大值.

解(1)p=2.(過(guò)程略)

評(píng)注以上兩道試題求解的關(guān)鍵在于用兩切線橫坐標(biāo)的和與積去銜接阿基米德三角形面積公式.這樣的思路不但可以避免求兩切點(diǎn)所在的直線方程、點(diǎn)到直線的距離及弦長(zhǎng),還能減少運(yùn)算,提高解題速度.

三、變式拓展

變式已知拋物線C:x2=4y,PA,PB為C的切線,切點(diǎn)為A,B.

(1)若點(diǎn)P在直線y=x-3上,求?PAB面積的最小值;

(2)若點(diǎn)P在雙曲線y2-x2=1的下支上,求?PAB面積的最小值．

解設(shè)點(diǎn)P(x0,y0),A(x1,y1),B(x2,y2),則x1+x2=2x0,x1x2=4y0.

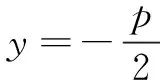
與此同時(shí),我們也能感受到,恰當(dāng)使用阿基米德三角形的性質(zhì)能簡(jiǎn)化運(yùn)算過(guò)程,減少運(yùn)算量,可以使一些較難的問(wèn)題得到比較方便的解決,從而提高……