由特殊到一般
——一道試題解答引發的思考

費曙光 何拓程

(北京市通州區運河中學,101121) (北京理工大學附屬中學,101119)

一、問題呈現

(1)求橢圓M的方程;

(2)過點F的直線l與橢圓M交于A,B兩點,BC⊥x軸于點C,AD⊥x軸于點D,直線BD交直線x=4于點E,求?ECD與?EAB的面積之比.

二、解法探究

1.以靜制動,特殊化探路

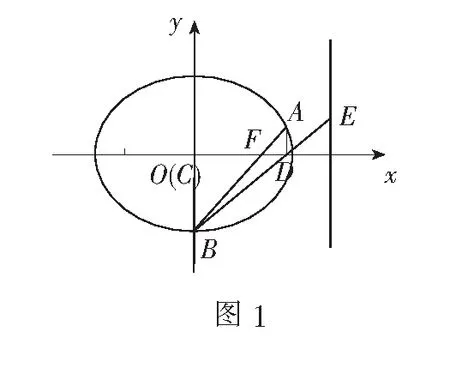
2.重點突破,一般性論證

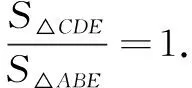
=0,

故C,A,E三點共線.

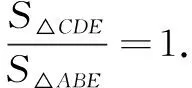
解法2設點A(x1,y1),B(x2,y2),C(x2,0),D(x1,0),同解法1證得C，A，E三點共線.

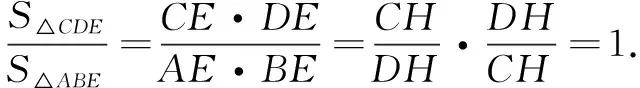
評注解法1和解法2立足于斜率證明C,A,E三點共線,思維方向是執因索果.我們也可以逆向思維,用同一法證明C,A,E三點共線.

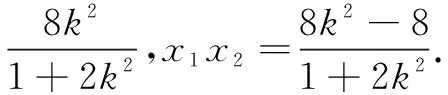
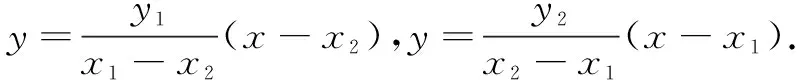
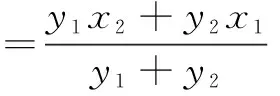
=4.

所以直線AC與BD交點的軌跡方程為x=4,即C,A,E三點共線.

三、背景溯源

回顧第(2)問的上述三種解法,可以發現C,A,E三點共線是隱藏在題設背后的一個重要的隱含條件,是解決問題的關鍵.注意到x=4為題設橢圓的右準線,由解法3進一步研究,不難發現C,A,E三點共線實質上源于以下一般性結論.

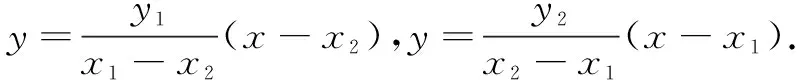
①

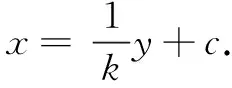
四、感悟

最新出臺的高考評價體系提出了基礎性、綜合性、應用性、創新性的“四翼”要求，其中綜合素質的培養要求學生對不同層面的知識、能力、素養能夠縱向融會貫通，合理組織和調動相關知識及能力，高質量應對復雜問題情境.通過以上問題的討論不難發現,當我們在問題求解遇到困難時,不妨先從簡單、特殊情形入手,挖掘問題的隱含條件,經歷直觀、猜想等思維過程,明確一般情形下解題的重點與難點,再圍繞重點尋找相關的數學模型與常見處理手段,關聯相應知識點,加深數學不同模塊的相互聯系,使知識與方法有效結合,達成問題的解答.