由教材案例談數(shù)學建模能力的培養(yǎng)*

顏美玲

(浙江省杭州外國語學校，310023)

一、問題的提出

近年來,作為我國高中數(shù)學課程的六大核心素養(yǎng)之一的數(shù)學建模越來越受到重視.新的課程標準也首次將數(shù)學建模活動與數(shù)學探究活動納入必修課程,并安排了具體的課時.有專家學者基于大樣本的測試數(shù)據(jù)發(fā)現(xiàn),我國學生的數(shù)學建模素養(yǎng)在六個數(shù)學核心素養(yǎng)中的測試平均分是最低的[1].

數(shù)學建模是應用數(shù)學解決實際問題的基本手段,也是推動數(shù)學發(fā)展的動力[2].這里所說的實際問題既包含現(xiàn)實世界中的實際問題,也包含數(shù)學內(nèi)部的實際問題.很多一線教師正在積極探討如何進行數(shù)學建模的課堂教學設計以及如何開展數(shù)學建模課堂教學等問題[3][4],讀后受益匪淺.與此同時,筆者也開始思考:除了主題式的數(shù)學建模教學,教材中有沒有值得我們一線教師好好開發(fā)利用的素材呢?本文以人教版《數(shù)學》必修第一冊P227中的例10——“扇形內(nèi)接矩形的面積問題”為例,與同行們共同探討如何利用教材例題培養(yǎng)學生的數(shù)學建模能力.

二、原題及教材用意分析

該例題在教材中呈現(xiàn)如下:

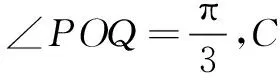
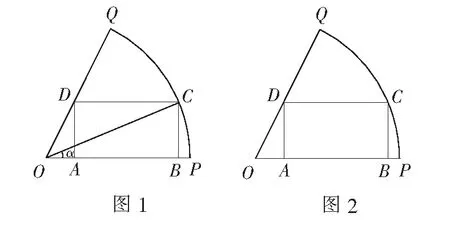
教材在第五章三角函數(shù)中的“簡單的恒等變換”第2課時中設置了如上例題.筆者覺得教材在此處設置該問題有兩個用意:一是在例9的基礎上,再通過具體的幾何問題讓學生掌握將形如y=asinx+bcosx的函數(shù)化為y=Asin(x+φ)的形式,進而求出最值等性質(zhì)的方法;二是促進學生對函數(shù)模型多樣性的理解,特別是讓學生感受以角……