“雙減”背景下優化初中數學作業設計的實踐探索

【摘要】本文基于“雙減”背景，論述減輕學生書面作業負擔應兼顧作業的適時與適量、優化作業設計應兼顧作業的多元與分層，并在以上實踐策略指引下，結合教學實踐案例，從精心設計基礎性統一過關作業、合理設計分層作業、適當設計實踐探究性作業三個層面總結了優化初中數學作業設計的經驗與做法。

【關鍵詞】“雙減” 初中數學 作業設計 優化

【中圖分類號】G62 【文獻標識碼】A

【文章編號】0450-9889（2022）16-0007-03

2021年7月，中共中央辦公廳、國務院辦公廳印發《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》（以下簡稱《意見》），為切實提升學校育人水平、持續規范校外培訓（包括線上培訓和線下培訓）、有效減輕義務教育階段學生過重作業負擔和校外培訓負擔（以下簡稱“雙減”）提供了政策支持。在此背景下，學校要提升育人水平，終究要落實到各個學科的課堂教學提質和課后作業優化上。

對學校教師來說，作業是反饋學生學習效果暨教師課堂教學效果的重要依據，在學科教學管理中發揮了重要作用。數學是一門嚴謹的學科，初中數學相對于小學數學而言具有更強的抽象性和邏輯性，數學教師應著力在課堂中培養和發展學生的學科素養和關鍵能力;同時通過布置課外作業，引導學生在完成作業的過程中進一步鞏固課堂所學知識，積累數學學習經驗、提高數學學習能力、發展數學學科核心素養。在“減輕義務教育階段學生過重作業負擔”的政策背景下，教師應積極探索作業設計優化的策略和方法。近年來，筆者基于作業設計“少而精”的原則，在時間上把控作業留多少、內容上考慮作業留什么、形式上選擇作業怎么留三個方面進行了扎實的實踐探索。

一、減輕學生初中數學書面作業負擔應兼顧作業的適時與適量

“適時”，主要指學生完成作業的時間要控制在合適的時間之內。有研究表明，完成作業的時間如果能夠控制在適當的時間內，能較好地達成檢測教學效果的目的;如果超出了學生的心理承受力，導致學生產生厭倦情緒，則不利于真實檢測教學效果。按照《意見》分類明確的各個學段的作業完成時間，初中生書面作業的平均完成時間應不超過90分鐘。也就是說，在初中階段，“適時”的書面作業完成時間總體“不超過90分鐘”。初中生課程多、課業重，各學科教師應合理分配學生書面作業的時間，給其他學科教師布置書面作業留有余地。鑒于數學學科對初中新開設的物理、化學等課程都具有基礎性作用，建議初中數學課后書面作業量控制在30分鐘以內，在確保學生養成良好學習習慣的基礎上提高作業完成的效率。

“適量”指的是作業的數量合適：過少，達不到檢測和鞏固課堂所學知識的效果，不利于促進學生數學思維的發展和綜合能力的提高;過多，則會加重學生作業負擔，導致學生休息時間不足、影響第二天的學習，甚至會導致部分學生對數學學科產生排斥心理，不利于培養學生的數學學習興趣。為了做到初中數學書面作業適時且適量，筆者給自己定下了一個不隨意布置教輔參考書上整頁作業“少而精”的原則：通常情況下，新授課的課后書面作業基礎過關題會根據知識的難易度精選5—8道不同水平層次的題目，其中解答題不超過3道，學有余力的學生可自由選擇做1—2道趣味性強的能力提升題。

二、優化初中數學作業設計應兼顧作業的多元與分層

綜觀數學學科傳統的課后作業，不僅作業形式單一，基本是書面作業，而且書面作業設計片面追求知識的覆蓋面，呈現出知識檢測碎片化、練習設計機械化等特點，如此對數學知識進行強化訓練和反復記憶，容易讓學生感覺枯燥乏味。要改變這一現狀，數學教師應秉持作業設計多元、分層的理念，統籌考慮作業內容的鞏固性、鮮活性、趣味性、拓展性、整合性、實踐性等綜合指標，整體提升作業的內容質量。首先是精心設計基礎性作業，原則是立足課標、著眼教材、科學規劃、力求精練;其次是合理設計分層作業，方法是精挑范例、合理改編;最后是適當設計綜合探究性作業，策略是注重聯系、變式拓展。多元、分層的作業設計，不僅有利于促進學生對所學知識的理解與內化，而且有利于打破死記硬背式作業對學生思維的束縛，既能開闊學生的眼界，又能促進學生數學思維的發展和學科素養的形成。基于作業內容和達成目標之間的關系，多元、分層作業還可以細分為預習準備型、積累練習型、延伸拓展型、開放創造型四種類型，如表1所示。

三、優化初中數學作業設計的實踐探索

（一）精心設計基礎性統一過關作業，促進學生數學思維的發展

1.在作業內容的變化中訓練學生思維的發散性與聚合性，引導學生體會數學“萬變不離其宗”之美

教學實踐中，筆者基于數學學科的特點，對書面作業設計中的基礎過關題進行了優化。首先，用好教材中的母題，設計基礎過關題，確保學生做一題通一片;設計能力提升題，以“一題多解”拓展學生的思維、以“多解歸一”聚合學生的思維，培養學生演繹推理和歸納推理的能力。例如，學生在學會用平方差公式進行因式分解后，教師可以設計如下有梯度的變式練習，鞏固學生所學基礎知識：（1）4x2-9;（2）16x2-81;（3）-16x2+81;（4）16x4-81;（5）16x3-81xy2;（6）16x2-81（y+z）2。該作業設計，從鞏固基礎知識的原題切入，按照“系數變→符號變→指數變→因式變→底數變”的變式規律，不斷強化學生對平方差公式的結構性認知，嘗試引導學生從不同的變式中感悟代數變式的規律，學會靈活運用平方差公式進行因式分解。學生在經歷“熟悉結構→改變形式→分解因式→檢查結果”的學習過程中逐步體會平方差公式中所蘊含的算理算法，掌握應用平方差公式進行因式分解的基本策略，積累相應的數學學習經驗。

2.在作業內容的變化中推動學生思維的進階發展，引導學生體會數學的理性之美

在“雙減”背景下，多數教師已經開始從作業的題量上去減輕學生的作業負擔，卻往往忽略了把控作業的難度：量少且難度降低，學優生吃不飽;量少且難度大，潛力生完不成。在筆者看來，作業設計優化必須首先考慮基礎知識、基本技能、基本思想和基本活動經驗“四基”的鞏固與拓展，方便學生切實獲得初中數學“四基”;其次是融會貫通，使學生能夠靈活運用所學數學知識和方法提高發現、提出、分析和解決問題的能力，發展“四能”;再次是拓展思維，通過數學題目的變式，對學生進行邏輯思維的強化訓練。事實上，數學學科以邏輯嚴謹、思維靈活、應用廣泛見長，數學應用與思維訓練的素材俯拾皆是，教師完全不必盲目追求“難題”“偏題”“怪題”。

例如，初中數學中的概念學習，其思維遞進便可以劃分為“基本概念與思想方法”“概念與方法的基礎應用”“概念與方法的延伸應用”“概念與方法的創新應用”四個階段。教師在設計作業時把握好同一份作業中不同問題之間思維遞進的特征，有利于促進學生教學思維的進階發展，提高學生問題解決過程中的思維靈活度。以絕對值的概念學習為例，針對學生的學習難點和易錯點，應用|a|的分類討論知識設計思維遞進式“去掉絕對值”作業（如圖1），先以基礎題1具體的數字變式鞏固學生對絕對值概念的認知，再設計題2—題4不確定的字母變式并使題目的不確定性逐漸升級，直至題5對含有絕對值的多項式進行化簡，這份作業緊扣絕對值的含義、性質，步步為營進行設計，不僅體現了由數到形、由具體到抽象的數學思維遞進特征，而且具有一定的開放性，切實達到了檢測思維靈活性的目的。

[1.[+3]=? ，[0]=? ，[-2]=? 。

2.①若[a]=5，則a=? 。②若[a]=[-5]，則a=? ;若[-a]=[-5]，則a=? 。

3.若[x]=-x，則x? 0。

4.若[2a-9]=9-2a，則a=? ?（寫出一個符合要求的正有理數）。

5.有理數a，b在數軸上對應點的位置如下圖所示。①結合數軸可知：-a? -b（用“>、=或<”填空）;②結合數軸化簡[b-a]-[a-1]+[1-6]=? 。

（二）合理設計書面分層作業，使不同層次的學生都能獲得學業進步

每一個學生都是一個鮮活、獨立的個體，其對新知吸收和掌握的程度會存在客觀上的差異性。如果教師按照“一刀切”的方式布置統一的書面作業，不利于對學生“因材施測”“對癥下藥”。因此，基于學生的知識掌握程度和學習能力差異對學生進行恰當的分層，針對不同層次學生設計出一份數量上有差異、難易上有不同的符合學生認知特點和學習需求的作業，以“階梯式題組”或“作業超市”的形式，合理設計“基礎+拓展”“基礎+彈性”“基礎+特色”的作業，可以確保每一個學生在每天的有效作業時間內都能完成適合自己的作業量，使不同層次的學生都能獲得完成作業的成就感，增強學好數學的信心。

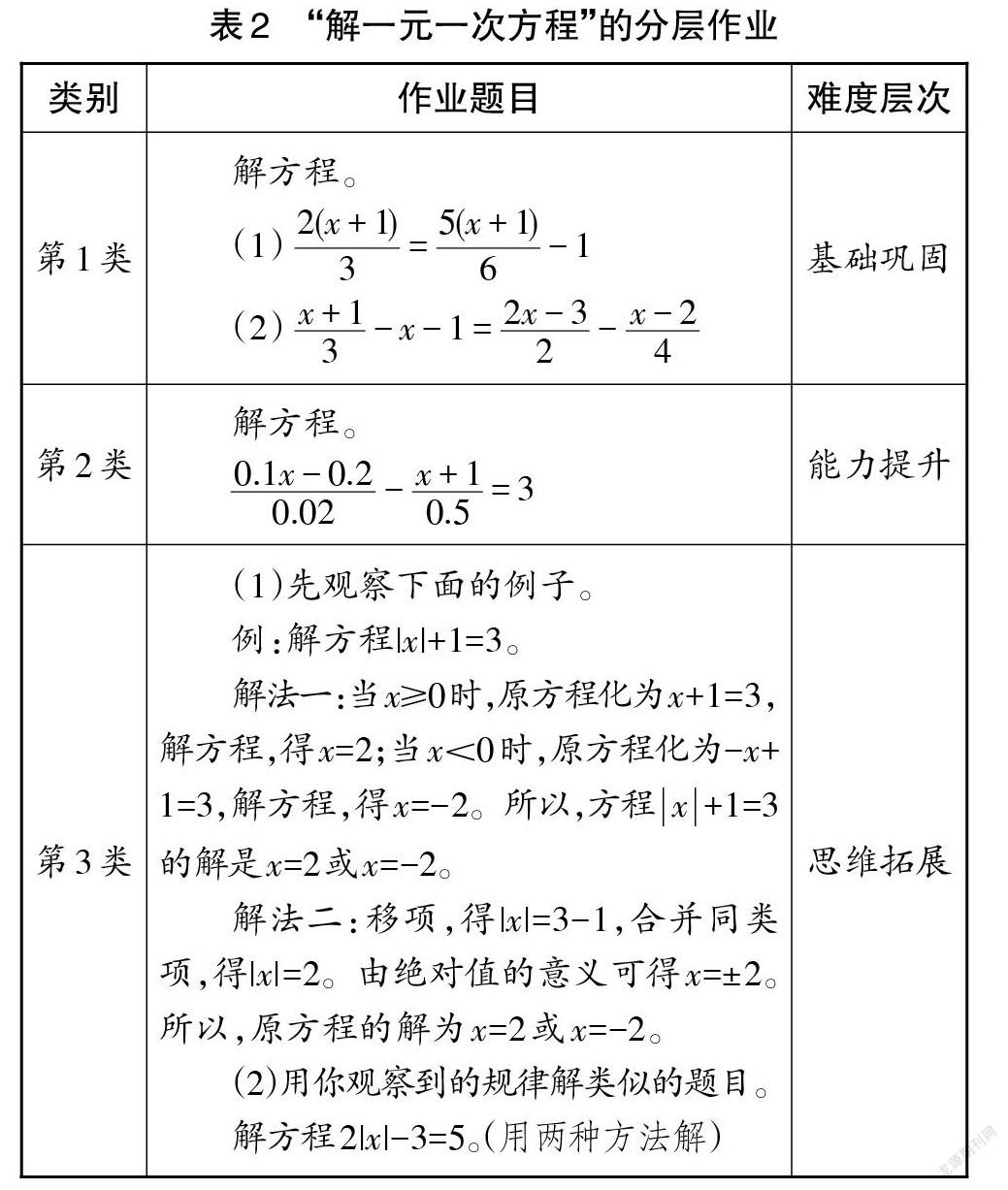
例如，在學生學完“解一元一次方程”之后，教師設計了包含有三個層次的分層作業（如表2），鼓勵學生在完成基礎知識訓練的同時，可以自由、大膽地選擇有挑戰性的感興趣的題目，開拓思維，遷移運用新知、形成新的解題技能。如此既降低了作業的“量”，又提升了學生挑戰難度作業的“欲”，使學生由“要我學”變成“我要學”，進一步強化了學生的學習動機。

（2）[x+13-x-1=2x-32-x-24] 基礎鞏固 第2類 解方程。

[0.1x-0.20.02-x+10.5=3] 能力提升 第3類 （1）先觀察下面的例子。

例：解方程|x|+1=3。

解法一：當x≥0時，原方程化為x+1=3，解方程，得x=2;當x<0時，原方程化為-x+1=3，解方程，得x=-2。所以，方程[x]+1=3的解是x=2或x=-2。

解法二：移項，得|x|=3-1，合并同類項，得|x|=2。由絕對值的意義可得x=±2。所以，原方程的解為x=2或x=-2。

（2）用你觀察到的規律解類似的題目。

解方程2|x|-3=5。（用兩種方法解） 思維拓展 ]

需要說明的是，教師設計分層作業時，應找準分層的依據，關注學生的心理需求，讓學生明白分層并不是對某些人有偏見，只是為了引導學生量力而行，選擇與自己能力水平相當或者比自身水平略高的作業，激發優等生的潛力，提高潛力生學好數學的信心。

（三）適當設計開放性實踐作業，體現數學教育的個性化追求

在筆者看來，數學作業除了用于夯實“四基”、提高“四能”的書面限時作業，還應將作業設計由“封閉”轉向“開放”，體現數學教育的個性化追求。在筆者看來，數學作業應避免出現“有知識，沒文化，缺素養”的現象。為此，數學教師需樹立“數學作業文化觀”，給學生設計一些需要經過一段時間團隊合作、探究完成的實踐探究任務，引導學生在實踐活動和數學知識的綜合運用中體悟數學文化與科技進步、數學知識與日常生活的密切聯系，發揮數學文化所承載的育人功能，進一步培養學生用數學的眼光觀察現實世界、用數學的思維思考現實世界、用數學的語言表達現實世界的數學學科核心素養。

在教學實踐中，筆者探索出一些體現數學文化育人的開放性實踐作業的設計方法，包括：結合課堂所學數學知識，布置學生閱讀相關數學家的故事并寫數學日記，以非限時課外實踐作業的形式，引導學生在閱讀中學習數學家堅持不懈追求真理的精神;結合課堂所學數學原理，布置學生進行相關的課外閱讀，引導學生了解歷史上的相關數學文化，同時以選擇題的方式對學生進行簡單的考查，強化學生對相關文化的數學認知（如圖2）;結合課堂所學知識設計網絡實踐作業，如安排學生查閱和統計2014—2018年中央財政累計投入“全面改善貧困地區義務教育薄弱學校基本辦學條件”的專項補助資金數目，先用科學記數法表示，再對數據進行分析并提出問題，完成一篇數學小論文，向同伴分享自己的感悟;等等。

[我國漢代的趙爽在注釋《周髀算經》時給出了勾股定理的無字證明，人們稱它為“趙爽弦圖”，“趙爽弦圖”指的是（? ）。

此外，現行教材中有不少“閱讀與思考”之類的閱讀資料，教師在設計開放性作業時，可以將教材中的閱讀資料整合進自己的作業設計當中，創設一些體現現實生活情境或數學文化情境，與學生知識結構、理解水平、心理特征相匹配，符合初中生興趣愛好和生活認知的項目式作業，拓寬學生的知識面和思維層次，培養學生正確的情感態度價值觀，對學生強化數學文化熏陶。例如，教材在關于物體高度測量的課程內容中介紹了一種利用三角形相似知識計算三角形邊長的測量思路，教師可以將該知識應用設計成一份實踐作業，讓學生實地測量校園里國旗旗桿的高度，提出測量方案并說明其合理性，引導學生學會遷移相關數學知識，積累數學活動經驗，在鍛煉動手實踐能力的同時，提高自主探究、團隊合作的意識，感受數學知識的應用價值。

總之，“雙減”減的是“負擔”，“少而精”的作業不會成為學生的作業負擔，它用教師的“勤”換來題目的“精”和學生的“輕”，通過量上精選、質上甄選、式上趣選，更精準地發揮了作業的綜合育人價值。作為教師，必須牢記“減負不減質”的基本原則，按照《意見》的提法，努力在“提高作業設計質量”上下功夫，切實“發揮作業診斷、鞏固、學情分析等功能”，為學校提升育人水平貢獻自己的智慧。

參考文獻

[1]任小清.初中數學課后作業設計的研究：以南充十中為例[D].南充：西華師范大學，2019.

[2]姚程琳.優化作業布置，鞏固學生知識：初中數學作業設計的相關思考[J].試題與研究，2021（18）：11-12.

[3]鐘紅，孫洪波，陶元.“雙減”背景下初三綜合復習數學作業內容設計初探[J].吉林省教育學院學報，2021（10）：103-106.

[4]張必華.“雙減”背景下數學教育的思考與建議[J].中學數學月刊，2022（1）：8-9.

[5]劉權華.“雙減”背景下數學教學應有的作業觀[J].教學與管理（中學版），2021（11）：64-66.

作者簡介：韋琴琴（1981— ），廣西上思人，高級教師，主要研究方向為中學數學教學。

（責編 白聰敏）