豐富作業類型，促進能力提升

孫紅波

［摘? 要］ 作業具有幫助學生鞏固所學知識、提升知識應用能力的功能，同時有助于教師對教學進行改革，提升教學的有效性. 因此，教師要重視作業設計，要豐富作業的類型，不僅要通過設計趣味性、開放性、分層性和實踐性的作業，激發學生的學習興趣，還要鼓勵學生參與自主編題，培養學生主動研究與合作學習的能力，從而提升學生的學習能力.

［關鍵詞］ 作業類型；學習能力；核心素養

教師不僅要進行知識的傳授，還要對學生的學習能力進行培養. 課堂教學要使學生在掌握知識的過程中保持一顆探索知識的好奇心，使學生成為一個終身學習者. 作業作為教學過程重要的一部分，不僅能培養學生獨立思考的能力，還能激發學生的創造精神和智慧潛能.

數學練習在數學學習中具有重要的意義，既是傳授數學知識的主要載體，又是提升學生創造能力、展現學生才能的主要手段. 學生在學習數學知識的基礎上，通過數學作業，能夠進一步鞏固知識，提升解題技能和思維能力. 因此，數學作業以及各種數學練習在學生的數學學習中占據著接近一半的時間，具有不可替代的意義. 但長期以來教師普遍將作業設計排在教學活動之外，對作業設計缺乏深刻的認識和整體的規劃，導致數學作業重視數量的積累而輕視質量的提升，學生在機械、重復的練習中失去了學習的興趣，這也影響了作業練習的效果. 筆者在教學實踐中對數學作業的設計進行了一些探索，下面圍繞作業設計的策略與各位同行進行討論.

趣味性作業設計，激發學生的自主學習興趣

新課標要求教學情境要貼近學生生活實際，要從學生熟悉的事物出發，激發學生的學習興趣，促進學生自主學習. 學生對作業是否感興趣，主要在于作業是否生動有趣，能否激發學生的好奇心. 形式單一、內容枯燥的作業只會讓學生感到枯燥乏味，提不起學習的興趣. 因此，教師要從學生的生活實際出發，設計貼近學生生活且形式新穎的作業，要符合學生的年齡特征和心理特征，內容具有創新性和趣味性，以此提高學生的自主學習能力［1］.

案例1“二元一次方程組應用”的趣味練習設計.

《天方夜譚》中有這樣一段文字：有一群小鳥，其中一部分在樹上唱歌，另一部分在地上找食物. 樹上的一只小鳥對著地上找食物的小鳥說：“假如你們飛上來一只，那么地上的小鳥數量就是所有小鳥數量的三分之一；假設從樹上飛下去一只小鳥，那么樹上的小鳥和地上的小鳥就一樣多了. ”你知道原來樹上和地上的小鳥分別有多少只嗎？

案例2? “混合運算”趣味練習設計.

“二十四點”游戲：（1）從1～13中任選四個自然數，將這些自然數進行加、減、乘、除運算，這四個數必須使用且只能使用一次，使這四個數的計算結果等于24；

（2）現有3，4，-6，10四個數，請你運用這四個數進行加、減、乘、除運算，使計算結果等于24；

（3）現有3，-5，7，-13四個數，請你運用這四個數進行加、減、乘、除運算，寫出一種運算式，使計算結果等于24.

上述兩個案例都通過趣味性的作業使學生在輕松的氛圍中鞏固了所學的知識，能讓本來較為枯燥的二元一次方程組應用與加、減、乘、除混合運算知識被學生愉快地掌握，能增強學生的閱讀能力，鞏固學生的“雙基”，培養學生按照規則運用知識解題的主動意識.

案例3“勾股定理的應用”趣味作業設計.

一個長方體盒子如圖1所示.

（1）用剪刀沿長方體的棱剪切，最少剪幾刀就能將這個長方體攤開成一個平面？

（2）有一只螞蟻正從點A向點B爬行，請你為這只螞蟻設計一條最短路線. 假設這個長方體的長、寬、高分別為5，3，4，這條最短路線的長是多少？

設計意圖這類題生動有趣，貼近學生的生活，能極大地調動學生的好奇心，激發學生的潛能，讓學生積極主動地完成作業. 這些試題與學生的生活息息相關，符合學生的年齡特征和心理特征，能讓學生養成觀察生活、研究數學的習慣，樹立學習數學的信心，明白“只要潛心鉆研，每個人都能成為發明家和創造者”.

分層作業設計，調動學習的積極性

每個學生都是獨立的個體，學習過程中存在差異，所以教師在教學中要因材施教，分層教學，滿足不同層次學生的需求，促進全體學生的發展. 教師在設計作業時，要注意按照不同層次的水平進行設計，由易到難，層層遞進，讓學生通過逐層問題探究知識、收獲知識，從而增強學習的自信. 分層作業能使學生找到適合自己的學習路徑，能讓不同層次的學生都有所收獲，從而促進學生共同發展.

案例4 ? “二次函數”分層作業設計.

已知拋物線y=x2+mx+m-5.

（1）證明：無論m為何值，拋物線與x軸始終有兩個不同的交點.

（2）當拋物線與x軸的交點都在原點的左側時，求m的取值范圍.

（3）當拋物線與x軸的兩個交點之間的距離等于5時，求m的值.

對于此題，第（1）問是基礎題，要求所有學生都要作答，第（2）問和第（3）問則可以要求學生選做. 對于學習能力較強的學生，完成基礎題之后可以讓他們思考富有難度的問題，從而滿足他們的好奇心，增強他們的學習成就感. 對于學習較為困難的學生，則要求他們掌握基礎知識即可，從而激發他們的學習興趣.

案例5? “相似三角形”分層作業設計.

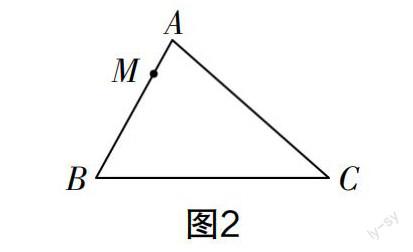
（1）如圖2所示，在△ABC中，AB=12，AC=16，點M在AB邊上，且MA=4，在AC上找一點N，使△AMN與△ABC相似，求出AN的長度.

（2）如圖3所示，在△ABC中，AB=AC，∠A=36°，∠ABC的平分線交AC于點D，求證：①BC=AD；②△ABC與△BDC相似.

（3）如圖4所示，正方形DEFG是△ABC的內接正方形，過點A作AM⊥BC，垂足為M，AM與DG交于點H. 若AH=4 cm，正方形的邊長為6 cm，求BC的長度.

對于此題，要求全體學生完成第（1）問，對于第（2）問和第（3）問，學生可以根據自己的能力自主選擇. 這樣的設計能讓不同的學生都體會到學習的樂趣，從而收獲成功的喜悅，增強學習的信心.

設計意圖“案例4”和“案例5”通過由易到難的分層作業，避免了“一刀切”，給學生提供了自主選擇的空間，既落實了學生的主體地位，又保護了學生學習的積極性，讓全體學生都獲得發展.

開放性作業設計，培養發散性思維

新課標倡導每個學生都找到適合自己的學習路徑，每個學生都學到有用的數學，在數學上獲得不同的發展. 因此，教師在設計作業時，要精選練習內容，選擇適合的練習形式，給予學生充分的思考空間和時間. 教師可以設計開放性作業，促進學生個性化發展，為學生的思維發展創造廣闊的空間，激發學生的發散性思維和求異性思維.

案例6? “四邊形”的開放性作業設計.

證明：取一個四邊形四條邊的中點，順次連接這四個點所得的四邊形一定是一個平行四邊形.

變式1：取一個矩形四條邊的中點，順次連接這四個點所得的四邊形是什么圖形？

變式2：取菱形、正方形、等腰梯形四條邊的中點，順次連接這四個點后所得的四邊形分別是什么圖形？

案例7? “菱形”的開放性作業設計.

如圖5所示，AE=AF，點B和點D分別在AE，AF上，四邊形ABCD是菱形，連接EC，FC，請用兩種方法證明EC與FC相等.

上述開放性作業，能培養學生整體思考問題的能力，能激發學生思維的創新性，能使學生在開放性的設問中激發潛能，充分發揮自己的能動性，提升思維能力. “案例6”通過變式練習培養學生從不同的角度思考問題和解決問題的能力，“案例7”則要求學生運用不同的方法解決問題，能提升學生的解題技能，深化學生對知識的理解.

案例8? “等腰三角形的性質”開放性作業設計.

試卷上有這樣一道題：在等腰三角形ABC中，AB=AC，小明不小心將墨水潑在試卷上，將這個等腰三角形的一部分遮住了，你有什么辦法將原來的等腰三角形ABC畫出來嗎？

學生看到這類試題覺得非常新穎，立馬有了興趣. 他們嘗試了多種方法，如通過作∠B=∠C畫出等腰三角形ABC；通過作BC的中垂線來畫出等腰三角形ABC；將等腰三角形進行對折，等等.

設計意圖開放性作業內容豐富、情境新穎、形式多樣、解題方法不拘一格，符合學生的心理特征，因此深受學生的喜愛. 并且開放性作業解題方法不唯一，甚至答案不唯一，因此可以激發學生從多個角度進行思考，有利于增強學生的創新意識.

實踐性作業設計，提升知識應用能力

知識的獲得只有在實踐中才能有真切的體驗和感受，所以教師要開展豐富多彩的實踐活動，引導學生將知識應用到更加廣闊的空間，從而提高數學應用能力.

案例9? “一次函數”實踐性作業設計.

當前大多數家庭都安裝了網絡，針對網絡收費問題，電信局有兩種收費方式，用戶可以自主選擇：第一種是計時收費，每分鐘0.05元；第二種是按月收費，每月54元，且需要加收每分鐘0.02元的通信費.

（1）某用戶某個月上網的時間為x（單位：min），設兩種收費方式的費用分別為y（單位：元）和y（單位：元），請寫出y，y與x之間的函數關系式；

（2）請你幫這個用戶計算采用哪種方式繳費更劃算.

學生結合實際使用情況，通過計算就可以在家庭使用網絡時做出更加合理的選擇.

設計意圖“案例9”引導學生利用已學知識解決生活實際問題，能讓學生體會到“數學來源于生活，又應用于生活”，能讓學生用數學的眼光去分析和解決生活實際問題. 實踐探究性作業能提高學生應用知識的能力，能提升學生的綜合素養.

學生自主設計作業，激發學習內驅力

新課標鼓勵每一個學生自主編題，成為“命題者”. 自主設計作業并完成作業，能加深學生對所學知識的理解，使學生以更寬闊的視野認識數學的本質，發展學生的思維，豐富學生的想象力，激發學生的內驅力.

案例10? “應用一元一次方程解決問題”學生自主編題設計.

師：我們學校的環形跑道長400 m，甲、乙兩名同學參加了1000 m長跑比賽，兩人以不同的速度跑完了全程. 請大家根據以上條件設計練習題并進行解答.

學生在設計練習并完成練習的過程中體會到了做學習主人的感受，并在教師的認可中收獲了自豪感，這能激發學生的創造性.

設計意圖學生自主設計作業可以有效地落實學生的主體地位，且在命題實踐中能更加深刻地理解知識. 在自主設計作業的過程中，教師要注重與學生的溝通，并且要引導學生加強與同伴的溝通和合作，從而提升學生的合作能力. 教師還可以讓學習水平在同一層次的學生結對，相互命題并完成練習，之后相互批閱，共同探討. 這樣，學生會在競爭意識下努力完成命題任務，并高質量地完成練習. 這樣的過程能消除學生對作業的固有印象，更好地發揮作業的功能. 可見，教師要轉變作業觀念，使學生成為作業的主人，讓學生在互動交往中學會學習、學會合作.

綜上所述，作業是課堂學習的延伸，是課堂教學的重要環節. 教師設計作業時，要以學生的發展為目標，要提高作業設計的質量，豐富作業的形式，注重作業的作用. 只有教師認真研究作業設計目標和作業形式，才能使作業符合新課標的要求，發揮學生的創造性和積極性，讓學生有更加廣闊的思考空間，讓學生感受到學習的樂趣，從而收獲數學學習的成就感，提升數學學習能力.

參考文獻：

［1］黃國才. 有效備課·上課·聽課·評課［M］. 福州：福建教育出版社，2010.