把握知識(shí)核心，定理探究教學(xué)

陸春燕

［摘? 要］ 幾何性質(zhì)定理的教學(xué)要把握好知識(shí)聯(lián)系，合理設(shè)計(jì)情境問(wèn)題引入課堂，精心設(shè)置探究環(huán)節(jié)，引導(dǎo)學(xué)生完成定理的探究論證，使學(xué)生掌握定理的同時(shí)提升素養(yǎng). 文章以“線段的垂直平分線的性質(zhì)”為例，展開(kāi)教學(xué)探討.

［關(guān)鍵詞］ 垂直平分線；性質(zhì)；聯(lián)系；探究；思想

“線段的垂直平分線的性質(zhì)”是初中幾何的重要內(nèi)容，對(duì)幾何知識(shí)體系的構(gòu)建有著重要的意義. 探究教學(xué)需要教師引導(dǎo)學(xué)生掌握垂直平分線的性質(zhì)及判斷方法，要求學(xué)生能夠靈活運(yùn)用性質(zhì)、定理解決實(shí)際問(wèn)題，同時(shí)教學(xué)中教師還要落實(shí)核心素養(yǎng)，提升學(xué)生的綜合能力. 下面基于教材內(nèi)容展開(kāi)教學(xué)反思.

把握知識(shí)聯(lián)系，情境設(shè)計(jì)引入

“線段的垂直平分線的性質(zhì)”是所學(xué)章節(jié)的重點(diǎn)，對(duì)于全新的知識(shí)，學(xué)生不知從何處開(kāi)始探究，因此，在探索引入階段，教師可以采用下面兩種方式：一是從知識(shí)聯(lián)系視角入手，關(guān)注知識(shí)的前后聯(lián)系；二是從情境視角入手，精心選擇情境素材，設(shè)計(jì)貼近學(xué)生生活的場(chǎng)景，引導(dǎo)學(xué)生逐步感知生活中的幾何性質(zhì).

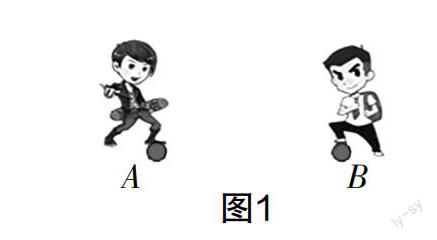
“線段的垂直平分線的性質(zhì)”的教學(xué)核心是一條線、兩端點(diǎn)、距離相等，情境問(wèn)題可以從“距離相等”衍生出“公平”，從而設(shè)計(jì)實(shí)際問(wèn)題引導(dǎo)學(xué)生思考，引出垂直平分線的性質(zhì). 所以教師可以設(shè)計(jì)如下問(wèn)題：如圖1所示，小明在點(diǎn)A處，小剛在點(diǎn)B處，兩人在玩搶禮物的游戲. 為了保證游戲公平，禮物應(yīng)放在什么地方？教學(xué)時(shí)教師應(yīng)引導(dǎo)學(xué)生發(fā)散思維，思考除了可以放在線段AB的中點(diǎn)處外，還可以放在哪些地方，從而引出線段垂直平分線的性質(zhì).

該章節(jié)的知識(shí)內(nèi)容，是在線段垂直平分線的概念和軸對(duì)稱性質(zhì)基礎(chǔ)上的進(jìn)一步探究，故教學(xué)線段的垂直平分線的性質(zhì)時(shí)，教師有必要進(jìn)行知識(shí)回顧、問(wèn)題設(shè)計(jì)等教學(xué)設(shè)計(jì). 問(wèn)題設(shè)計(jì)建議采用遞進(jìn)設(shè)問(wèn)的方式，引導(dǎo)學(xué)生逐步深入. 基于“線段AB展示→軸對(duì)稱分析→作垂直平分線”來(lái)構(gòu)建的問(wèn)題鏈如下.

問(wèn)題1：圖2所示的線段AB是軸對(duì)稱圖形嗎？

問(wèn)題2：請(qǐng)指出圖2中線段AB的垂直平分線.

問(wèn)題3：可以采用哪些方法來(lái)繪制線段AB的垂直平分線？

教學(xué)中，教師要引導(dǎo)學(xué)生從軸對(duì)稱的視角看待線段AB，深刻體會(huì)線段的軸對(duì)稱性質(zhì). 在此基礎(chǔ)上，教師要讓學(xué)生思考線段垂直平分線的作法，引導(dǎo)學(xué)生采用測(cè)量、翻折兩種方法來(lái)作線段的垂直平分線. 其中測(cè)量法分“取中點(diǎn)”“作垂直”兩步，翻折方法則滲透了軸對(duì)稱的性質(zhì). 整個(gè)教學(xué)過(guò)程教師要充分結(jié)合“操作實(shí)踐”與“引導(dǎo)思考”，讓學(xué)生在實(shí)踐中重溫垂直平分線的概念、軸對(duì)稱的性質(zhì)等知識(shí)，體會(huì)知識(shí)的生長(zhǎng)過(guò)程，逐步過(guò)渡到性質(zhì)探究.

重視探究過(guò)程，精設(shè)探究環(huán)節(jié)

“線段的垂直平分線的性質(zhì)”屬于幾何性質(zhì)探究?jī)?nèi)容，教學(xué)中建議教師精心設(shè)計(jì)各個(gè)環(huán)節(jié)，引導(dǎo)學(xué)生體驗(yàn)新知的獲得過(guò)程，充分調(diào)動(dòng)學(xué)生的思維，使學(xué)生掌握幾何性質(zhì)的同時(shí)獲得思維的提升. 故教學(xué)中建議教師采用過(guò)程探究的方式，讓學(xué)生參與活動(dòng).

性質(zhì)探究需要完成“猜想驗(yàn)證”到“結(jié)論歸納”整個(gè)閉環(huán)過(guò)程，即教師要引導(dǎo)學(xué)生分析直觀圖形，做出猜想，然后利用相關(guān)知識(shí)驗(yàn)證，從中提取結(jié)論完成性質(zhì)歸納. 設(shè)計(jì)教學(xué)環(huán)節(jié)時(shí)需要遵循兩大原則：一是關(guān)注學(xué)情，把握學(xué)生的認(rèn)知規(guī)律，讓知識(shí)自然生成；二是豐富探究過(guò)程，注重思維引導(dǎo)，提升學(xué)生的思維水平. 教師教學(xué)“線段的垂直平分線的性質(zhì)”時(shí)，可設(shè)計(jì)如下探究活動(dòng).

1. 活動(dòng)1：分析關(guān)系，問(wèn)題猜想

在“性質(zhì)猜想”環(huán)節(jié)，教師需要引導(dǎo)學(xué)生直觀感知，通過(guò)獨(dú)立思考來(lái)做出猜想，故教學(xué)時(shí)建議設(shè)計(jì)圖形問(wèn)題，直觀對(duì)比其中的數(shù)量關(guān)系，引導(dǎo)學(xué)生猜想.

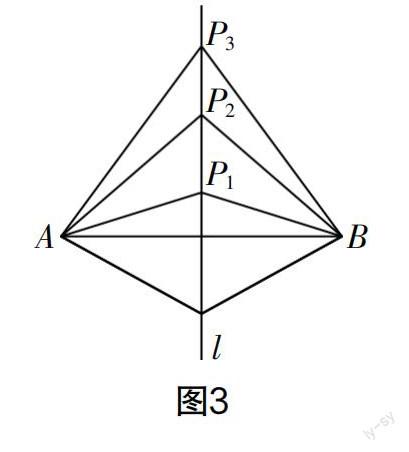
預(yù)設(shè)：給出如圖3所示的圖形，假定直線l為線段AB的垂直平分線，P1，P2，P3均是直線l上的點(diǎn)，觀察P1，P2，P3三點(diǎn)到點(diǎn)A和點(diǎn)B的距離，分析其中的數(shù)量關(guān)系.

引導(dǎo)設(shè)計(jì)：此環(huán)節(jié)需要學(xué)生理解其中的位置關(guān)系，即l是AB的垂直平分線，故該直線經(jīng)過(guò)AB的中點(diǎn)，并與AB垂直. 接著直接探討線段之間的數(shù)量關(guān)系，即AP1與BP1、AP2與BP2、AP3與BP3之間的數(shù)量關(guān)系. 學(xué)生通過(guò)觀察，可以初步感知到它們的長(zhǎng)度相等，即線段AB垂直平分線上的P1，P2，P3三點(diǎn)到點(diǎn)A和點(diǎn)B的距離相等.

2. 活動(dòng)2：動(dòng)手操作，推理驗(yàn)證

“猜想驗(yàn)證”環(huán)節(jié)是基于上述猜想進(jìn)行的探究驗(yàn)證，該環(huán)節(jié)要結(jié)合感性分析與理性推理，引導(dǎo)學(xué)生多角度論證，故可采用操作實(shí)踐、幾何證明兩種方式進(jìn)行教學(xué).

（1）操作驗(yàn)證：測(cè)量、對(duì)折.

教學(xué)中，教師可引導(dǎo)學(xué)生用直尺分別測(cè)量AP1，BP1，AP2，BP2，AP3，BP3的長(zhǎng)度，進(jìn)而得出結(jié)論. 也可以沿直線l折疊線段AB，讓學(xué)生觀察AP1與BP1、AP2與BP2、AP3與BP3是否重合. 顯然，若兩兩重合，則表示它們分別相等.

（2）幾何證明：全等性質(zhì).

教師還可以引導(dǎo)學(xué)生通過(guò)判斷對(duì)應(yīng)三角形全等的方法來(lái)完成證明. 假定線段AB的中點(diǎn)為C，以分析△AP1C和△BP1C為例，教師可引導(dǎo)學(xué)生證明這兩個(gè)三角形全等. 從已知出發(fā)，因?yàn)镃是線段AB的中點(diǎn)，所以AC=BC. 因?yàn)橹本€l是線段AB的垂直平分線，所以∠P1CA=∠P1CB=90°，結(jié)合P1C=P1C，可得△AP1C≌△BP1C（SAS），進(jìn)而可推出AP1=BP1.

顯然上述推理適用于點(diǎn)P1不在線段AB上的情形，即兩個(gè)三角形存在；而當(dāng)點(diǎn)P1在線段AB上時(shí)，點(diǎn)P1與AB的中點(diǎn)C重合，顯然有AP1=BP1. 教學(xué)中，教師要注意培養(yǎng)學(xué)生的推理分析能力，讓他們養(yǎng)成嚴(yán)謹(jǐn)思考的習(xí)慣.

3. 活動(dòng)3：語(yǔ)言描述，性質(zhì)歸納

通常，幾何性質(zhì)可以用文字語(yǔ)言和幾何語(yǔ)言來(lái)概括，故歸納性質(zhì)時(shí)，教師要引導(dǎo)學(xué)生用這兩種語(yǔ)言來(lái)描述，以提升學(xué)生對(duì)性質(zhì)的理解. 基于上述驗(yàn)證，學(xué)生可得到如下結(jié)論.

幾何語(yǔ)言：如圖4所示，直線l⊥AB，垂足為C，AC=CB，點(diǎn)P在l 上，則PA=PB.

文字語(yǔ)言：線段垂直平分線上的點(diǎn)到這條線段兩個(gè)端點(diǎn)的距離相等.

教學(xué)中，對(duì)于幾何結(jié)論，為了理解性質(zhì)、定理，教師要引導(dǎo)學(xué)生根據(jù)幾何結(jié)論繪制對(duì)應(yīng)的圖像，結(jié)合幾何條件提取幾何特征，由幾何結(jié)論分析幾何性質(zhì). 對(duì)于文字結(jié)論，教師要引導(dǎo)學(xué)生關(guān)注命題的“題設(shè)”與“結(jié)論”，對(duì)性質(zhì)定理進(jìn)行拆解，如對(duì)于線段垂直平分線的文字結(jié)論，教師可把它拆分成題設(shè)與結(jié)論，其中題設(shè)為一點(diǎn)在線段的垂直平分線上，結(jié)論為該點(diǎn)到這條線段兩個(gè)端點(diǎn)的距離相等. 對(duì)于該命題，教師還可以引導(dǎo)學(xué)生逆向思考，結(jié)合等腰三角形的“三線合一”來(lái)推導(dǎo)幾何結(jié)論.

4. 活動(dòng)4：性質(zhì)應(yīng)用，知識(shí)強(qiáng)化

“知識(shí)應(yīng)用”環(huán)節(jié)有助于強(qiáng)化對(duì)性質(zhì)的理解，故問(wèn)題設(shè)計(jì)既要立足于性質(zhì)定理，又應(yīng)注重問(wèn)題變式，于是教師教學(xué)時(shí)可從兩大視角進(jìn)行引導(dǎo)探究：一是利用逆定理作線段的垂線；二是利用性質(zhì)定理證明推理.

預(yù)設(shè)問(wèn)題1：如圖5所示，已知直線AB和直線AB外的一點(diǎn)C，請(qǐng)用圓規(guī)和無(wú)刻度的直尺作直線AB的垂線，且垂線經(jīng)過(guò)點(diǎn)C.

問(wèn)題引導(dǎo)：此問(wèn)題已知直線垂線上的一點(diǎn)，為了得到垂線，需要知道垂線上另一點(diǎn)的位置，故可參考線段垂直平分線的逆定理，即找到直線AB上的兩點(diǎn)，且點(diǎn)C到這兩點(diǎn)的距離相等，再以這兩點(diǎn)構(gòu)成的線段為底，作任意的等腰三角形. 等腰三角形的另外一個(gè)頂點(diǎn)就是所求的垂線上的另一點(diǎn). 作圖痕跡如圖6所示.

預(yù)設(shè)問(wèn)題2：如圖7所示，在△ABE中，D，C兩點(diǎn)均在BE上，且AD⊥BE，BD=DC. 若點(diǎn)C在AE的垂直平分線上，試分析AB，AC，CE之間的數(shù)量關(guān)系，以及AB+BD與DE之間的數(shù)量關(guān)系.

問(wèn)題引導(dǎo)：由線段垂直平分線的性質(zhì)定理可直接推出AC=EC，AB=AC，進(jìn)而可得到AB=AC=CE. 對(duì)于AB+BD與DE之間的數(shù)量關(guān)系，可由等量代換得AB+BD=CE+CD=DE，即AB+BD= DE.

合理滲透思想，提升綜合素養(yǎng)

數(shù)學(xué)思想是解決問(wèn)題的重要工具，在幾何定理教學(xué)中，教師同樣要重視數(shù)學(xué)思想的滲透. 在教學(xué)環(huán)節(jié)合理滲透數(shù)學(xué)思想，能讓學(xué)生逐步感知到數(shù)學(xué)思想，從而提升學(xué)科素養(yǎng). 教學(xué)“線段的垂直平分線的性質(zhì)”時(shí)，教師需要重點(diǎn)滲透從特殊到一般、分類討論和數(shù)形結(jié)合三大思想.

以“線段的垂直平分線的性質(zhì)”探究為例，在“推理驗(yàn)證”環(huán)節(jié)，線段的垂直平分線上的點(diǎn)的選擇就可以滲透從特殊到一般的思想，即先設(shè)定“特殊性”的定點(diǎn)，再?gòu)摹耙话阈浴钡慕嵌葋?lái)探索點(diǎn)的位置變化時(shí)的結(jié)論；在“推理驗(yàn)證”環(huán)節(jié)可滲透分類討論思想，培養(yǎng)學(xué)生思維的嚴(yán)謹(jǐn)性，即對(duì)于線段垂直平分線上的點(diǎn)，可分點(diǎn)在線段上和點(diǎn)不在線段上兩種情形，然后分別構(gòu)建模型進(jìn)行推理驗(yàn)證；在“知識(shí)應(yīng)用”環(huán)節(jié)則可以滲透數(shù)形結(jié)合思想. 特別地，對(duì)于數(shù)學(xué)思想，教師在教學(xué)中還要注重解題思路的引導(dǎo)，以下面的問(wèn)題為例：

如圖8所示，在△ABC中，AB的垂直平分線交AB于點(diǎn)E，交BC于點(diǎn)D，連接AD. 已知△ADC的周長(zhǎng)為13 cm，AC=5 cm，試求BC的長(zhǎng)度.

思想引導(dǎo)：引導(dǎo)時(shí)需要分兩個(gè)過(guò)程——以“形”釋“數(shù)”和由“數(shù)”照“形”，即結(jié)合圖形理解條件，把握?qǐng)D形特征，挖掘幾何關(guān)系，再由代數(shù)推導(dǎo)結(jié)論.

在教學(xué)環(huán)節(jié)滲透數(shù)學(xué)思想，能為新知賦予“思想”特性，有助于學(xué)生感悟、理解定理，讓學(xué)生的思想進(jìn)一步升華，從而提升綜合素養(yǎng). 不過(guò)，數(shù)學(xué)思想較為抽象，所以教師在教學(xué)中要把握其中的精髓，立足知識(shí)規(guī)律，利用數(shù)學(xué)思想指導(dǎo)探究，幫助學(xué)生積累探究經(jīng)驗(yàn).

總之，教學(xué)“線段的垂直平分線的性質(zhì)”時(shí)，教師要把握知識(shí)核心，以知識(shí)探究的方式開(kāi)展教學(xué)探討，且探究過(guò)程圍繞“距離相等”全方位構(gòu)建幾何模型，多方式、多角度地進(jìn)行論證展示. 教學(xué)中教師還要關(guān)注學(xué)生的思維活動(dòng)，利用引導(dǎo)性問(wèn)題推進(jìn)教學(xué)，融合知識(shí)教學(xué)與素養(yǎng)培養(yǎng)，從而提升學(xué)生的綜合能力.