分散難點，解決二次函數最值問題

秦虹柳

【摘要】在實際教學中，筆者發現“二次函數的應用”問題對于學生來說是個很難跨越的障礙，有很多學生只要碰到這類問題就表現出嚴重的畏難情緒，還有一些學生在面對即使是很基礎的問題時，也無從下筆.尤其是“二次函數中最值”的問題，更是學生難以突破的屏障.

【關鍵詞】二次函數;最值問題;數學解題

在教學中，老師們都會重點強調二次函數的最值問題與頂點之間的聯系，如二次函數y=ax2+bx+c（a≠0），當x=-b2a時，函數取最值y=4ac-b24a.但是，對于一個二次函數限定不同定義域時的最值問題，才是學生們的學習難點，這應該引起教師的關注，我們可以通過如下的教學設計來幫助學生充分理解二次函數的最值問題.

例如 “當x滿足如下條件時，x為何值時，函數 y=x2-2x+3取最值，最值是幾？”

（1）x取全體實數;（2）2≤x≤3;

（3）22;

（5）x≥2;（6）x≤3;

（7）x<3;（8）0≤x≤3;

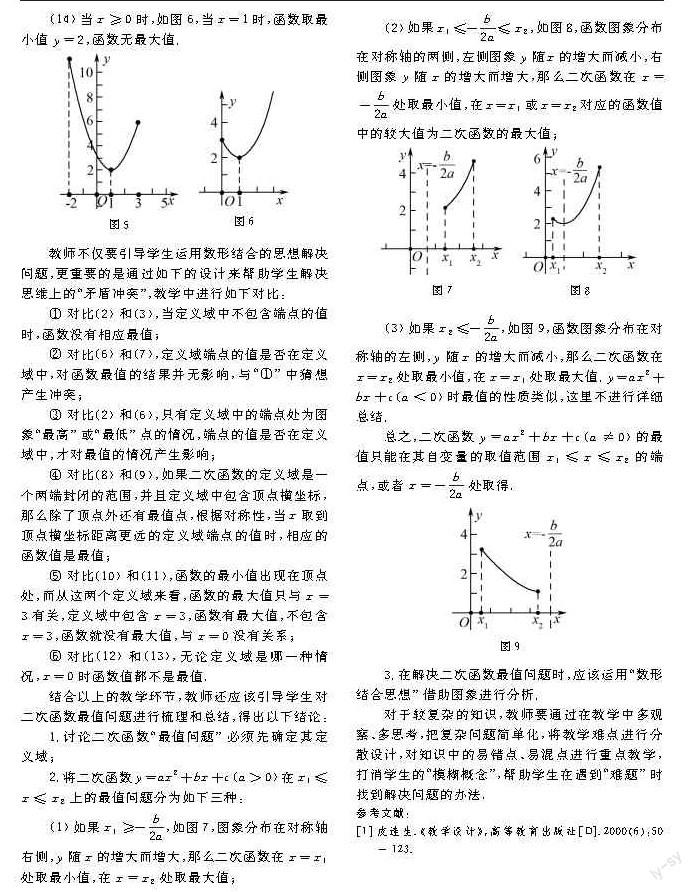
（9）-2≤x≤3;（10）0

（11）0≤x<3;（12）0

（13）x>0;（14）x≥0.

在二次函數最值問題的教學中，應該特別強調“數形結合”的思想，通過圖象幫助學生理解最值問題，y=x2-2x+3的圖象如圖1，易求：該函數頂點坐標為（1，2），根據不同定義域，結合具體函數圖象，引導學生分析結果如下：

（1）當x取全體實數時，如圖1，當x=1時，函數最小值y=2，函數無最大值;

（2）當2≤x≤3時，如圖2，當x=2時，函數最小值y=3;當x=3時，函數最大值y=6;

（3）當2

（4）當x>2時，函數無最小值，也無最大值;

（5）當x≥2，當x=2時，函數最小值y=3，無最大值;

（6）當x≤3時，如圖3，當x=1時，函數取最小值y=2，無最大值;

（7）當x<3時，當x=1時，函數取最小值y=2，無最大值;

（8）當0≤x≤3時，如圖4，當x=1時，函數取最小值y=2;當x=3時，函數取最大值y=6;

（9）當-2≤x≤3時，如圖5，當x=1時，函數最小值為y=2;當x=-2時，函數最大值為y=11;

（10）當0≤x<3時，當x=1時，函數取最小值y=2，函數無最大值;

（11）0

（12）當0

（13）當x>0時，當x=1時，函數取最小值y=2，函數無最大值;

（14）當x≥0時，如圖6，當x=1時，函數取最小值y=2，函數無最大值.

教師不僅要引導學生運用數形結合的思想解決問題，更重要的是通過如下的設計來幫助學生解決思維上的“矛盾沖突”，教學中進行如下對比：

①對比（2）和（3），當定義域中不包含端點的值時，函數沒有相應最值;

②對比（6）和（7），定義域端點的值是否在定義域中，對函數最值的結果并無影響，與“①”中猜想產生沖突;

③=3＼*GB3對比（2）和（6），只有定義域中的端點處為圖象“最高”或“最低”點的情況，端點的值是否在定義域中，才對最值的情況產生影響;

④對比（8）和（9），如果二次函數的定義域是一個兩端封閉的范圍，并且定義域中包含頂點橫坐標，那么除了頂點外還有最值點，根據對稱性，當x取到頂點橫坐標距離更遠的定義域端點的值時，相應的函數值是最值;

⑤對比（10）和（11），函數的最小值出現在頂點處，而從這兩個定義域來看，函數的最大值只與x=3有關，定義域中包含x=3，函數有最大值，不包含x=3，函數就沒有最大值，與x=0沒有關系;

⑥對比（12）和（13），無論定義域是哪一種情況，x=0時函數值都不是最值.

結合以上的教學環節，教師還應該引導學生對二次函數最值問題進行梳理和總結，得出以下結論：

1.討論二次函數“最值問題”必須先確定其定義域;

2.將二次函數y=ax2+bx+c（a>0）在x1≤x≤x2上的最值問題分為如下三種：

（1）如果x1≥-b2a，如圖7，圖象分布在對稱軸右側，y隨x的增大而增大，那么二次函數在x=x1處取最小值，在x=x2處取最大值;

（2）如果x1≤-b2a≤x2，如圖8，函數圖象分布在對稱軸的兩側，左側圖象y隨x的增大而減小，右側圖象y隨x的增大而增大，那么二次函數在x=-b2a處取最小值，在x=x1或x=x2對應的函數值中的較大值為二次函數的最大值;

（3）如果x2≤-b2a，如圖9，函數圖象分布在對稱軸的左側，y隨x的增大而減小，那么二次函數在x=x2處取最小值，在x=x1處取最大值.y=ax2+bx+c（a<0）時最值的性質類似，這里不進行詳細總結.

總之，二次函數y=ax2+bx+c（a≠0）的最值只能在其自變量的取值范圍x1≤x≤x2的端點，或者x=-b2a處取得.

3.在解決二次函數最值問題時，應該運用“數形結合思想”借助圖象進行分析.

對于較復雜的知識，教師要通過在教學中多觀察、多思考，把復雜問題簡單化，將教學難點進行分散設計，對知識中的易錯點、易混點進行重點教學，打消學生的“模糊概念”，幫助學生在遇到“難題”時找到解決問題的辦法.

參考文獻：

[1]皮連生.《教學設計》，高等教育出版社[D].2000（6）：50―123.