化歸思想在三角函數解題中的應用

秦艷萍

【摘?要】??三角函數是高中數學的重要知識點，涉及較多的概念與公式.相關習題情境復雜多變，應用的解題思想不盡相同.其中在化歸思想指引下解題可達到化難為易，提高解題效率的目的.教學實踐中應做好化歸思想相關理論知識的講解，結合具體例題為學習者展示針對不同題型如何進行化歸.

【關鍵詞】???劃歸思想;高中數學;三角函數

1?方程向函數的轉化

方程與函數關系非常密切??[1] .將方程向函數轉化的目的在于運用函數的圖象、性質降低方程問題難度，以達到順利解題的目標.需要注意的是解答三角函數習題時應注重三角函數圖象的特殊性，能夠準確的分析與判斷出三角函數的對稱軸、對稱中心、周期等相關內容.另外，針對部分三角函數習題，還需要配合使用整體思想，從整體上把握相關參數之間的內在關聯.

例如???已知關于x的方程（?sin?x+?cos?x）??2?+?cos?2x=m在區間（0，?π?]上存在兩個相異實根x??1?，x??2?，且|x??1?-x??1?|≥??π??4?，則實數m的取值范圍為（??）

（?A?）[0，2）.??????（?B?）[0，2].

（?C?）[1，?2?+1].???（?D?）[1，?2?+1）.

因為?sin???2?x+?cos???2?x=1，2?sin?x?cos?x=?sin?2x，所以（?sin?x+?cos?x）??2?+?cos?2x=m時可得?sin?2x+?cos?2x=m-1，由輔助角公式可得?sin?（2x+??π??4?）=??2??2?（m-1）.令t=2x+??π??4?，即，?sin?t=??2??2?（m-1）在區間（??π??4?，?9?π??4?]上有兩個不同的實根t??1?，t??2?，作出y=?sin?t（??π??4

2?函數向方程的轉化

函數向方程轉化在高中數學解題中也較為常用，只是對于大多數學習者而言很少關注.函數向方程轉化主要結合函數上某一點構建相關等式關系.函數向方程轉化主要用于解決函數圖象相交、函數零點等問題.??[2] 實踐中為使學習者掌握轉化的相關規律，應注重在課堂上多與學習者互動，多啟發學習者，通過引導使其能夠自己頓悟，如此才能使其真正的掌握，內化為自身能力.

例如???已知函數f（x）=|?cos?x|（x≥0）的圖象和過原點的直線剛好有四個交點，設其中最大交點的橫坐標為θ，則?2θ?（1+θ?2）?sin?2θ?的值為（??）

（?A?）-2.??????（?B?）-1.

（?C?）0.????（?D?）2.

根據題意可知直線和f（x）=|?cos?x|（x≥0）在區間（?3?π??2?，2?π?）的圖象相切，此時f（x）=?cos?x，相切時對應的橫坐標最大，切點坐標為（θ，?cos?θ）.由導數知識可得f′（x）=-?sin?x，則直線的斜率為?-?sin?θ?，則對應的方程為y-?cos?θ=-?sin?θ（x-θ）.整理得到y=-x?sin?θ+θ?sin?θ+?cos?θ.而該直線過原點，即，θ?sin?θ+?cos?θ=0，解得θ=-?cot?θ，?則?2θ?（1+θ?2）?sin?2θ?=?-2?cot?θ?（1+??cot???2θ）?sin?2θ?=?-2?cot?θ?（1+??cot???2θ）?sin?2θ?=-?1???sin???2θ+??cos???2θ?=-1，選擇（?B?）.

3?數向形的轉化

數、形是高中數學研究的兩個非常重要的對象.兩個對象在某種層面上具有統一性，解答三角函數時關注兩者的統一性，實現彼此之間的轉化，是解題的重要思路.??[3] 其中結合“數”并聯系所學想象與畫出對應的圖形，可降低“數”運算的復雜程度，提高計算正確率.教學實踐中應注重為學習者匯總與三角函數相關的圖形，實際掌握畫相關三角函數圖象方法，夯實其畫圖的基本技能，為數向形順利地轉化，高效地解題奠定基礎.

例如???已知函數f（x）=2?sin?（ωx+φ）（ω>0，-??π??4?<φ

（?A?）8.??（?B?）9.??（?C?） 10.??（?D?）11.

根據題意結合三角函數性質可知f（x）=2?sin?（ωx+φ）的最小正周期為2，則ω=?2?π??T?，又因為f（0）=0，-??π??4?<φ

4?形向數的轉化

解答三角函數習題時有時需要將形轉化數.但是僅僅知道這一點是不行的，還需要掌握轉化的思路，轉化后數據的處理.其中形向數轉化的思路較多，在三角函數部分主要借助正余弦定理進行轉化，以構建與圖形相關的數量關系.當然在處理數據時還應注重挖掘與運用圖形中的隱含條件，把握圖形變化中線段、角度的變化邊界.

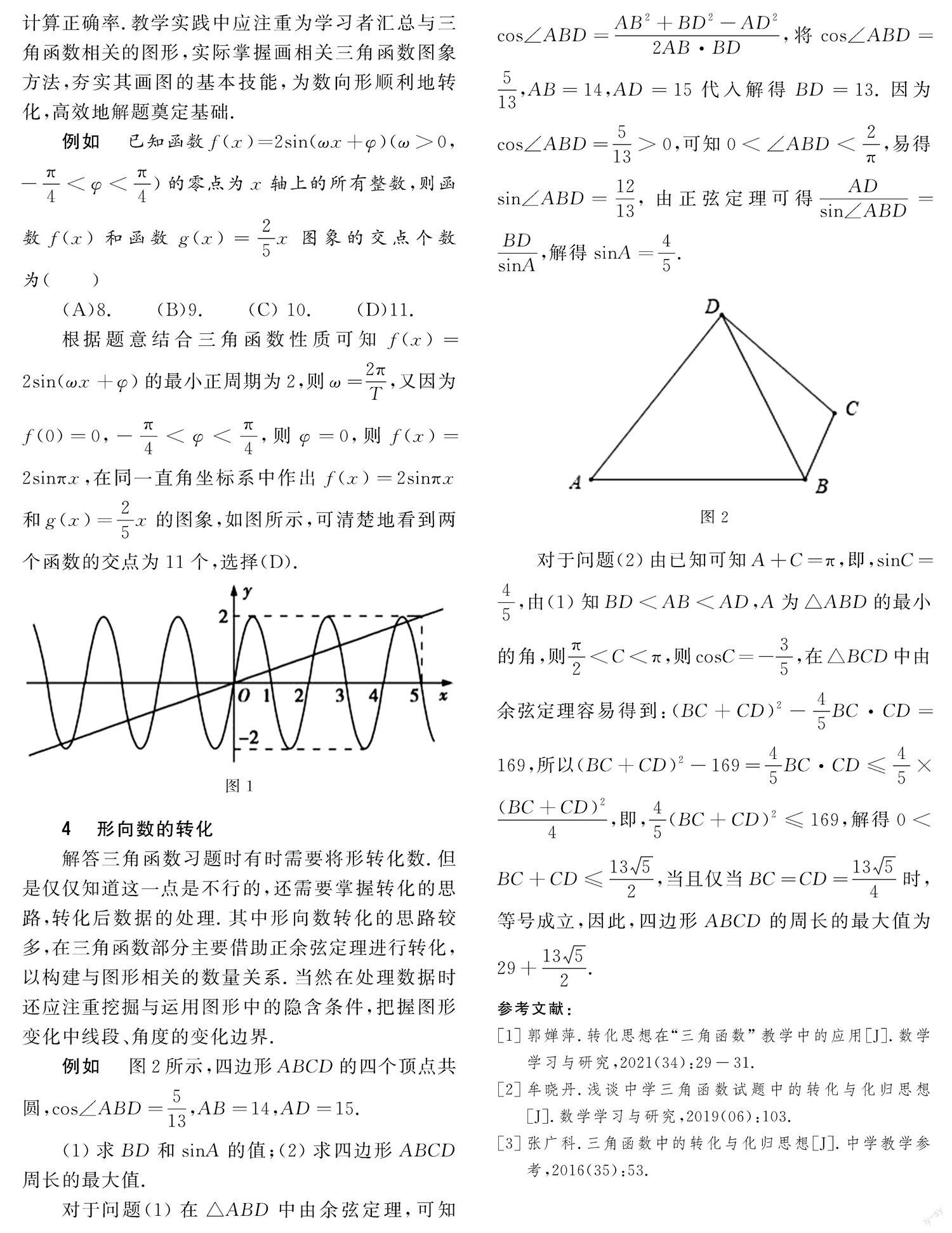
例如???圖2所示，四邊形ABCD的四個頂點共圓，?cos?∠ABD=?5?13?，AB=14，AD=15.

（1）求BD和?sin?A的值;（2）求四邊形ABCD周長的最大值.

對于問題（1）在△ABD中由余弦定理，可知?cos?∠ABD=?AB?2+BD?2-AD?2?2AB·BD?，將?cos?∠ABD=?5?13?，AB=14，AD=15代入解得BD=13.因為?cos?∠ABD=?5?13?>0，可知0<∠ABD

對于問題（2）由已知可知A+C=?π?，即，?sin?C=?4?5?，由（1）知BD

參考文獻：

[1] 郭嬋萍.轉化思想在“三角函數”教學中的應用[J].數學學習與研究，2021（34）：29-31.

[2]牟曉丹.淺談中學三角函數試題中的轉化與化歸思想[J].數學學習與研究，2019（06）：103.

[3]張廣科.三角函數中的轉化與化歸思想[J].中學教學參考，2016（35）：53.