依托“閱讀與思考”,提升數學味,凸顯素養觀

樓凌吉

[摘 ?要] “閱讀與思考”匯集了數學知識的源起、發展、完善和應用，展示了古今中外的數學魅力，而在緊湊的進度下，其價值得不到充分的發揮，甚至淪為教材中的“邊角料”. 文章以“圓錐曲線的光學性質及其應用”探究為例，在實踐操作中發展直觀想象素養，在探索求證中提升邏輯推理素養和數學運算素養，在實際生活問題的分析中提升數學抽象素養和數學建模素養. 研究者以為開展“閱讀與思考”教學研究，可在數學文化中滲透數學思想和方法，隔離“數學畏”，提升“數學味”，激發學生學習數學的主觀能動性，實現核心素養的螺旋式上升.

[關鍵詞] 閱讀與思考;數學文化;數學味;主觀能動性;核心素養

[?]改善閱讀現狀，隔離“數學畏”

近幾年，數學文化在高考試題中頻頻出現，不管是浙江卷的一小段，還是全國卷的大篇幅，只要看見文字材料，學生心里就充斥著“數學畏”. 學生堆積如山的書籍中，除了教材和教輔資料，基本見不著數學課外閱讀書籍的身影;在網絡平臺上，學生為數學消耗的流量少之又少. 數學閱讀意識和主動性的缺乏，究其根本是學生對數學的畏懼，甚至是抗拒. 同時，教師隊伍中能被學生冠以“×神”的多半是數學教師. 看不見摸不著，卻又時刻縈繞在心，有崇敬之意更有畏懼之心，在學生心中，神一樣存在的不是數學教師，而是數學本身.

結合學生的認知發展，利用教材的每一板塊，打磨教學的各個環節，研究如何將數學從“有畏”變成“有味”，數學教師責無旁貸. 在教學實踐中，筆者發現“閱讀與思考”在新授課階段，往往因為進度問題被擱置，而到了高三復習階段，隨著教材成為壓箱之物，其再次淪為“邊角料”. 據初步了解，一線數學教師對“閱讀與思考”進行深入研究的并不多，能和學生一起開展研究性學習的更是寥寥無幾.

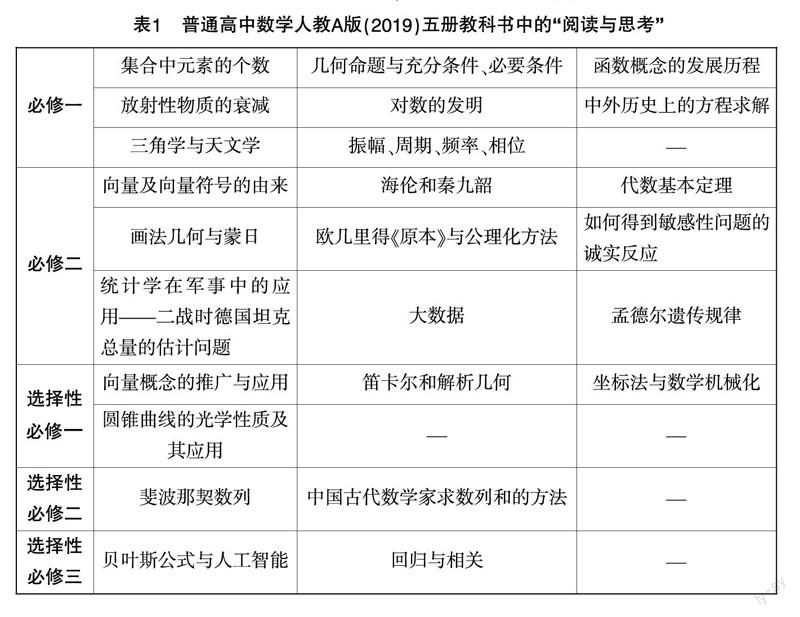
筆者羅列了普通高中數學人教A版（2019）五冊教科書中的“閱讀與思考”的標題（見表1），單從標題上看就足以刺激學生的味蕾. 它匯集了數學知識的源起、發展、完善和應用，展示了古今中外的數學魅力. 抽象的數學概念、巧妙的數學方法、深奧的數學思想，其起源和發展都是自然的，不僅合情合理，還富有人情味，這在情感上拉近了學生和數學的距離.

以下是筆者的一堂源于“閱讀與思考”的探究性教學片段，展示它和大家一起感受“數學味”.

[?]“閱讀與思考”教學案例分析——以“圓錐曲線的光學性質及其應用”為例

數學教學不只在于傳授公式和定理，更在于激勵學生從數學的角度去發現問題、思考問題、解決問題，進而建立數學學習自信心. 本節課通過創設具體生動的問題情境，點燃思維火花;類比圓的反射過程，經歷觀察、猜想、論證三部曲探究拋物線的光學性質;在互助合作中完成橢圓光學性質的探究;了解光學性質在生活中的應用，將理論上升到實踐，感悟學習數學是有用的;以探究雙曲線的光學性質為課后作業，進一步鞏固解析幾何的思想方法，體會圓錐曲線的統一性. 在教學過程中努力提升“數學味”，發展學生的核心素養，提升其獨立獲取數學知識的能力，增強學生學習數學的興趣和學好數學的信心，培養其鍥而不舍的鉆研精神和科學態度.

1. 創設情境，引入課題

師：浙江省紹興柯巖風景區的蓮花聽音景點是全國最大的石蓮花，由99塊巨石拼鋪成半徑為9.9米的圓形. 對著石蓮花的是一堵圓弧形的回音壁，相傳坐在蓮花中心對著回音壁誦念經文可以和佛心共融共振. 我在游玩時對著回音壁說話，真的可以聽到回音，但為什么只有站在蓮花中央時，回音才是最明顯的？

在回顧光的反射定律后，教師引導學生從情境問題中抽象出數學模型：從圓心射出的光線經圓反射后，反射光線再次經過圓心，基本解決開篇提出的問題.

師：大家只作出了入射光線和反射光線，請問法線在哪里？法線又是如何確定的？

在導數學習中，學生學習了用曲線上某點處的切線近似替代這一點附近的曲線，即“以直代曲”的思想方法. 在教師的引導下，學生能自然引進圓在入射點處的切線所在面作為反射面，再依次作出法線和反射光線.

師：回音有強弱之分能用圖形來說明一下嗎？

在交流合作中，產生了對照組（如圖1所示），可以清晰地看到站在圓心A處能接收到更多的反射光波. 期間，教師要引導學生多做幾組光線的反射，從A和B射出的光線，若只畫一條經C處反射的光線，就無法解釋回音的強弱. 因此，多次試驗，仔細觀察和認真分析可以找到一般規律. 積累從具體到抽象的活動經驗，養成在日常生活中一般性思考問題的習慣，把握事物的本質，以簡馭繁，運用數學抽象的思維方式思考并解決問題[1].

2. 精準作圖，大膽猜想

類比圓中的光線反射問題，接下來研究從圓錐曲線的焦點射出的光線經曲線反射后的特點. 為使學生方便作圖，教師在學案上印有精確的圓錐曲線，并標出焦點的位置. 同樣，精確性也體現在學生的作圖過程中，直尺是必需的，有量角器自然是極好的.

先從拋物線入手，學生依次作出入射光線、拋物線在入射點處的切線、法線和反射光線. 作完一條光線的反射線后，學生并沒有發現當中蘊含的光學性質. 回顧上一環節，強調多次試驗才能摸索出它們的共性，隨后選取幾張反射光線近乎平行的練習予以展示，最后將手動的探索過程轉移到幾何畫板上，動態的演示使學生更加直觀地感受到拋物線的光學特點，并大膽猜想：從焦點射出的光線，經拋物線上的一點反射后，反射光線平行于拋物線的對稱軸.

3. 層層推進，分析論證

經歷直觀感受和大膽猜想，下一步就是分析論證. 如圖2所示，從拋物線y2=2px的焦點F射出一條光線，經曲線上一點A（x，y）反射，求證反射光線平行于x軸.

要證明反射光線平行于x軸，即證明∠2=∠3，即證明∠1=∠3，即證明AF=BF.

因為拋物線y2=2px在點A（x，y）處的切線方程為yy=p（x+x），所以相應的法線方程為y-y=-（x-x），所以法線與x軸相交于點B（x+p，0），所以BF=x+=AF.

在證明過程中，學生進一步掌握了等價轉化思想方法，鞏固了拋物線的定義和在某點處的切線方程，經歷了用代數方法解決幾何問題的三部曲.

4. 明確結論，實踐應用

通過上述的直觀感受和分析論證，學生掌握了拋物線的光學性質. 在進一步介紹拋物面反射鏡后，教師展示了2021年10月18日在希臘奧林匹亞的赫拉神廟前采集北京冬奧會火種的圖片，并請學生思考其中的原理. 教材中還有許多拋物線光學性質的應用，這使學生感受到數學與生產生活的緊密關系.

5. 遷移方法，探究新知

以探究拋物線的光學性質為例題，橢圓的光學性質研究則是一個習題，通過“問題鏈”鞏固研究橢圓光學性質的過程、方法和思想.

問題1：從橢圓的一個焦點射出的光線，經橢圓上的一點反射后，反射光線有什么特點？

問題2：怎么證明從橢圓的一個焦點射出的光線，經橢圓上的一點反射后，反射光線經過橢圓的另一個焦點？

問題3：如何利用橢圓的光學性質解釋電影放映機的工作原理？

部分學生通過作圖認為反射光線經過橢圓的中心，有學生馬上提出異議：當選取橢圓的上頂點作為入射點時，反射光線經過另一個焦點. 得到此錯誤結論，究其原因，首先是作圖不精確，其次是光線的條數過于單一. 精準作圖，多次試驗，結合特殊到一般的推理過程，不少學生能挖掘出橢圓的光學性質.

如圖3所示，要證明法線AB為∠FAF的平分線，只要證明=.

因為橢圓+=1（a>b>0）在點（x0，y0）處的切線方程為+=1，所以相應的法線方程為y-y=（x-x0），所以法線與x軸相交于點B

x，0，所以==. 又

AF===x+a，同理

AF= -x+a，故=.

數學運算素養是最基本的素養，學生通過數學運算能力的發展，可以有效促進其數學思維的發展，進而養成科學嚴謹、求真務實的重要品質[2].

6. 課堂小結

通過把蓮花聽音中的回音問題抽象化、數學化，學生學會了光線反射到圓上的研究方法，并把它類比到圓錐曲線中，通過精準作圖，大膽猜想，嚴格論證，發現了拋物線和橢圓的光學性質，了解了它們在實際生活中的應用，感受到了數學的強大“磁場”. 在研究過程中，要注重學生直觀想象、邏輯推理、數學運算等核心素養的發展，在生活實際問題的分析中提升數學抽象素養和數學建模素養.

7. 教學反思

本節課提出了一些具有挑戰性的問題，凸顯了自主探究、合作交流等學習方式，部分學生并不能很好地適應，顯得有些束手無策. 冰凍三尺，非一日之寒，這意味著教師在日常的課堂教學中還沒有真正把主動權交給學生. 在有限的時間內，學生完成計算橢圓上的點到焦點的距離有一定的困難，可以先將教材中的“信息技術應用——用信息技術工具探索點的軌跡：橢圓”作為預備知識，了解圓錐曲線的第二定義，簡化計算曲線上的點到焦點的距離，不僅為圓錐曲線光學性質的研究提供便捷，而且從離心率的角度再次體現圓錐曲線的統一性.

[?]依托“閱讀與思考”，提升“數學味”，凸顯素養觀

學生經過中考分層，學習能力不相上下，并處于同一學習環境，而經過三年的時間，分差可以從中考的二十幾分上升到幾百分. 這期間，學生的主觀能動性起著主導作用，能否主動、獨立甚至富有創造性地學習不僅決定著他們的高考分高低，更決定著他們是否可以持續發展. 在現實生活、日常情境中，數學無處不在，常常日用而不自知，對數學模型的感知、判斷、思考和應用，在一定程度上決定著我們的智性水平、理性高度和文野之分[3]. 數學教學切不可就題論題，停留在抽象的層面，否則極易引起學生的“數學畏”. “閱讀與思考”給師生提供了教學素材，指明了教學方向，提升了“數學味”，凸顯了素養觀.

1. 數學可以追尋歷史，放眼未來

數學是一面鏡子，用數字、符號和圖形折射出過去和未來. 在《放射性物質的衰減》中，引進良渚遺址中發掘的草裹泥來研究水壩的修建時間，進而刷新對中國文明起源的認知. 良渚古城被列入世界遺產，良渚文化得到國際社會的普遍認可離不開碳元素檢測，它比其他史料和考古都更具說服力. 《放射性物質的衰減》文末還提出：如果函數呈指數增長，那么稱函數值增長為原來的兩倍所用的時間為“倍增期”. 將倍增期的概念和當下人口問題相結合，提出計算人口倍增期的兩種方法：①p=pekn，②p=p（1+k）n，其中p為n年后的人數，p為原有人數，k為人口年增長率，n為經過的年數，當=2時，求得的n就是人口倍增期. 查閱過去幾十年中國人口總數，經過函數擬合，預測20世紀80年代若無實行計劃生育的情況下人口自然增長的倍增期，體會數學在國家宏觀調控上的價值.

2. 數學可以洞察萬物，精準反饋

數學是一部探測儀，可以強力分辨、準確定位隱埋在深處的問題. 《統計學在軍事中的應用——二戰時德國坦克總量的估計問題》介紹了用不放回抽樣來估計離散型均勻分布最大值，強調統計方法的精確性和有效性是常規情報收集方法無法比擬的. 學習了《如何得到敏感性問題的誠實反應》，學生可以自己動手設計問卷，開展考試作弊、校園欺凌等敏感性問題的調查. 《孟德爾遺傳規律》在概率統計的指引下開啟了遺傳學的大門，洞察到外在表象下隱含著的生命密碼. 《大數據》依托數據和數據分析結果做出決策，影響著人們的生活方式，例如每天的天氣預報. 近年來，教育事業快速發展，全面步入“智慧教育”新時代，其中一個方面就是大數據精準教學.

3. 數學可以化繁為簡，高效運作

數學善于思考問題的共性，提出高效的解決方案，是計算機技術的基礎和核心，是最強大腦. 《中國古代數學家求數列和的方法》介紹了北宋數學家沈括為了求一層層壘起的酒壇總數，提出了二階等差數列的一個求和公式，即“隙積術”，為后續“垛積術”的研究奠定了基礎. 學習《向量概念的推廣與應用》，借鑒材料中校服廠家定制服裝的過程，學生可以就班服的購買問題進行一次數學實戰演練，選考技術的學生還可以根據所學的知識編寫一套程序，高效解決這一問題. 這些“閱讀與思考”可以讓學生深刻地體會到數學在解決實際問題中的有效性.

[?]結語

“閱讀與思考”的教學研究活動可以促使學生從實際背景抽象出數學問題，建立數學模型，運用數學語言表達問題，用邏輯推理解決問題，進一步指導實踐，極大地活躍學生的數學思維. “閱讀與思考”的課堂富有問題性、抽象性、推理性、探索性，充滿著“數學味”. 高中數學教學以發展學生的核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質[4]. 數學雖源于對現實世界的抽象，但在教學過程中不能只有抽象，還應時時刻刻回顧其與社會生活的關系，為社會創造的價值. “閱讀與思考”真正體現了這一要求. 因此教師應將“閱讀與思考”教學落到實處，提升“數學味”，凸顯素養觀，充分發揮學生的主觀能動性，使學生以更高的熱情投身于數學學習.

參考文獻：

[1] ?中華人民共和國教育部. 普通高中數學課程標準（2017年版2020年修訂）[M]. 北京：人民教育出版社，2020.

[2] ?王娟，李保臻. 基于數學運算能力培養的單元教學設計研究——以初中“因式分解”內容為例[J]. 中學數學教學，2019（04）：1-6.

[3] ?裴亞光. 數學教學是圓夢之旅——在湖北大學第四屆（2017）數學文化節上的報告[J]. 中學數學教學參考，2019（25）：2-4.

[4] ?中華人民共和國教育部. 普通高中數學課程標準（2017年版2020年修訂）[M]. 北京：人民教育出版社，2020.