創生修正，體驗積淀

蘇娜 王圣昌

學習不應停留在對知識的表層理解與機械式重復訓練中，教師要基于知識的內在結構和整體特性，以知識為載體，以問題為主線，引導學生從知識學習走向思維發展。“許多時候學生在數學課堂上表現得消極與被動，是因為教師沒有引領學生真正學會用數學的眼光看世界，學生在課堂上只能靜坐、聽從、接受，進行各種訓練，沒有自主思考的時間。”[1]王圣昌老師執教的《正方形數的秘密》一課，讓學生自主經歷創新修正的過程，在體驗中積累經驗、積淀智慧，給一線教師帶來了深刻的啟示。

該課的目標定位是：利用學具操作，可視化理解（a+b）2≠a2+b2，并在“形”的幫助下自主探索，深入理解為什么（a+b）2=a2+2ab+b2。王老師把目標拆解成精準有效的任務，通過學習、操作、交流、修正，讓學生慢慢體驗“式”與“形”的內在聯系，進而主動表征（a+b）2和a2+2ab+b2的意義。掌握這一知識本身不是教學的目的，而是教學的載體，通過這一載體讓學生經歷建構模型的過程，是本節課真正的價值所在。

【教學片段賞析】

（一）借助學具，初步建立“式”與“形”的聯結

課堂上，教師為每位學生都準備了可以相互連接的不同顏色的小立方體學具。教學伊始，簡單的課前交流后，教師在屏幕上呈現了第一個活動任務“請思考如何用學具表示2×（2+3）”。

師：看屏幕上的活動要求，有不明白的地方嗎？

生：可以直接表示2×5嗎？

生：不可以，因為2+3分開表示，說明它們不是一組的，如果表示成5的話，就變成一組了。

師：非常好！還有問題嗎？沒有，那就開始吧！

（學生獨立操作學具后，教師引導學生進行交流）

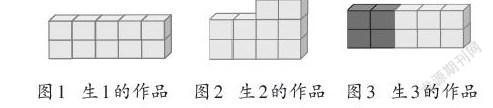
師（呈現生1、生2的作品，如圖1、圖2）：哪個比較符合題目的要求？

生：我覺得生2的作品比較符合要求。生1的作品可以直接用算式2×5表示，生2的作品可以用算式2×2+2×3表示。

生3：我覺得生2的作品也不合適，題目要求用學具表示2×（2+3），生2的作品沒有表示出這個算式的意思來。我認為應該這樣（出示自己的作品，如圖3）。

師：誰能看懂他的意思？你同意哪一個？

生：我同意生3的，他用不同的顏色表示，左邊深色的表示的是2×2的意思，右邊淺色的表示的是2×3的意思，合起來就表示出算式2×2+2×3的意思。

生：我也同意生3的，一行有（2+3）個小立方體，有2行，所以是2×（2+3）。

學生進入真正的思考狀態，是學習發生的重要標志。教學要呈現知識本身的屬性，還原學習的本質，讓學生更多地經歷知識的形成過程，發展學生的能力。以上教學片段中王老師巧妙地利用學具資源，把要達成的學習目標設計成合理的學習任務——“如何用學具表示2×（2+3）”。在這一活動中，學生不只是進行了操作，還通過與同伴間的交流，不斷發現“式”與“形”的聯結點，明晰2×5和2×2

+2×3的拼搭方式不能夠完全表達算式的含義，進而在辨析中找到并理解能夠表達2×（2+3）這個算式意義的正確圖形。在這個創生修正的過程中，學生既經歷了模式的識別，也實現了活動經驗的有效積淀，逐漸積累一種思維的方法和經驗。

（二）自主操作，嘗試辨析式與式的區別

在學生建立了“式”與“形”之間的聯結，能夠用學具表達算式的意義后，教師提出第二個活動任務“（2+3）2和22+32是否相同？請用學具操作、畫圖說明或算式解釋等方法表達你的想法”。

師：先思考10秒鐘，想想你的答案是什么，你打算怎樣說明你的結論，然后開始。你將有5分鐘的時間來呈現你的想法。

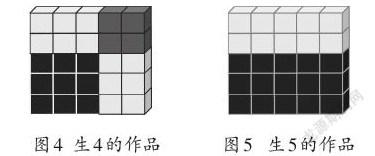
學生操作后，教師呈現生4的作品（如圖4），并在引導學生思考這幅圖的意思后，請生4解釋。

生4：我的結論是（2+3）2和22+32不相同。我用學具擺圖形來說明。我擺的圖形可以看作是一個大正方形，它的邊長是2+3，所以面積就是（2+3）2。其中右上角正方形的面積是22，左下角正方形的面積是32，所以它們的面積不相同。

生：我來補充。大正方形的面積（2+3）2比其中兩個小正方形的面積22與32的和還多出了2個長方形，也就是多了2×（2×3）。

教師繼續出示生5的作品，引導：有同學也得到了同樣的結論，并用這樣一幅圖（如圖5）表示了他的想法。看一看，你有什么想說的？

生：我覺得不能這樣表示。雖然看起來總數是一樣的，但是圖表達的算式的意思不相同。這幅圖上半部分表示的意思是2×5，下半部分表示的意思是3×5，合起來應該是（2+3）×5。圖中看不到22和32。

師：怎么改能讓大家看到（2+3）2和22+32？

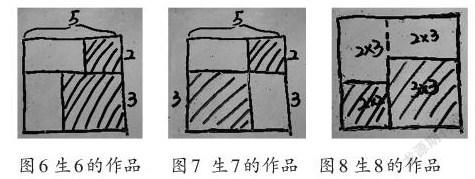
生6一邊板書（如圖6）一邊解釋：這里是22，這里是32，加起來是22+32，旁邊還多出了兩個2×3的長方形。

生7：還可以這樣畫（如圖7）。整個圖形的面積是（2+3）2，右上是22，左下是32。這和用學具擺差不多，可以更清楚地看出（2+3）2和22+32不相等，多出了兩個2×3的長方形。

生8：這樣畫更清楚，大家看（如圖8）……

本片段的教學，如果教師只停留在讓學生進行（2+3）2和22+32這兩個算式的比較上，那么學生也只會就數論數，不知道為什么這樣算，根據什么來算，這樣算表示什么。而王老師將目標拆解成多個層次的體驗式學習任務，讓學生針對困惑點“（2+3）2和22+32是否相同”，用學具、圖形、算式表達自己的想法，說出自己的理由，注重借助“形”去發現“式”的不同與相同，挖掘數學本質，再在“形”的基礎上構建模型。在這個過程中，學生充分經歷了“多元表征”“數形結合”的過程，主動傾聽、交流、思考，從感知到認知，實現了學習體驗的有效積淀。

（三）思考歸納，獨立嘗試建構模型

在學生借助學具、圖形充分感知算式意義的基礎上，教師呈現第三個活動任務“請畫圖表示（2+4）2，并用等式表示（2+4）2=？”。

學生獨立寫出等式“（2+4）2=22+42+2×2×4”以后，小組內進一步借助圖形交流算式中每一個數表達的意思。

本環節中學生對數學知識的“再發現”過程可謂水到渠成。正因為有了之前的小組合作、操作探究、討論研究等師生間的交往互動，學生的思考逐步深入。他們通過一次次有效的數學活動，在思維碰撞、表達反思、抽象總結的過程中，真正理解了算式的含義。

【對小學數學課堂教學的啟示】

知識的習得不能僅通過填充、記憶、鞏固練習來完成，教師的教學應關注學生的理解，讓學生在獲得每一個結論之前都經歷深入觀察、思考、質疑、操作、驗證、總結的“再創造”過程。分析王老師的課，可以在以下幾個方面給一線教師的課堂教學帶來啟示。

（一）有效拆解，讓操作路徑清晰明了

數學學習過程是一個具體的行為過程，其主體是學生。教師應將學習目標拆解成能夠讓學生經歷、體驗的有效學習任務，為學生的理解與生生之間經驗的互動創造寶貴的機會。如這節課中，王老師沒有講“和平方”的知識點，也沒有要求學生一定要掌握“和平方”的結論，而是設置了“請思考如何用學具表示2×（2+3）”“（2+3）2和22+32是否相同？請用學具操作、畫圖說明或算式解釋等方法表達你的想法”“請畫圖表示（2+4）2，并用等式表示（2+4）2=？”這一系列層次遞進的、可操作的體驗式任務，讓學生在完成任務的過程去發現、比較、建構、遷移、應用，在不斷創生修正中，有效積淀學習體驗。在這種過程性學習中浸潤成長的學生，會形成無論面對何種問題都要尋根問底的深度思考習慣。學生一旦形成穩定而獨特的學習特征，就標志著學科核心素養已初步形成。

（二）順學而教，尊重真實學習自然發生

法國思想家、教育家盧梭倡導教育要回歸自然。順其自然教數學，將人的天性與教育相融合，把內在的“自然”發展要求融入教育實踐中，注重啟發引導，鼓勵學生積極參與學習活動，主動建構和完善知識結構。[2]課堂上王老師尊重學生的真實起點，順學而教，他創設的每一個任務都從學生的真實發展區切入，鼓勵學生大膽嘗試;以輕松、自然的交流方式深入，讓學生在極具安全感的課堂教學環境中暢所欲言，不斷修正。要使學生像數學家那樣去思考，就要給予學生自我探索、提出猜想、做出假設、檢驗結論、進行反駁、調整策略、設計方案、歸納總結、論證結論的機會。創建這樣的學習環境，將會促進學生數學創造力的發展。[3]

（三）提供支持，讓獨立學習成為可能

學生的學習不是憑空可以達成的，教師要為學生搭建合適的腳手架，提供合適的幫助與支持，讓學生的獨立學習成為可能。本節課上，王老師為學生提供的學具都是有效的支持工具，幫助學生實現了思維的“可視化”，讓學生對算式意義的理解主動而深入。王老師借助學具的直觀拼搭，將“式”與“形”進行聯結，從2×（2+3）的數形聯結到（2+3）2和22+32式、形的比較與辨析，每一次王老師都不急于呈現答案，而采用先拼搭、體驗、交流，再驗證的方式加以創生修正，深度挖掘數學本質，依托可視化的直觀呈現，化抽象為具體，變無形為有形。通過幾何直觀，幫助學生建立畫面感，讓學生充分感知形與數、形與式，進而建構模式、應用模式，進行識別、創造，助力學生更深刻地理解數學知識。

作為一線數學教師，我們在這節課中看到了真實的學習發生過程。我們在教學過程中都應當“忌急”“忌表”，寓積極于無為，以無為成就有為，尊重教育規律，積淀深度學習體驗，尋求深刻、真實的數學學習。

參考文獻：

[1]周斌.立足課堂讓深度學習自然發生[J].數學學習與研究，2021（23）：24-25.

[2]高叢林.“順其自然”教學的內涵與策略探微[J].小學數學教師，2020（6）：15-17.

[3]謝明初，王尚志.數學創造力的特征、培養與研究展望[J].全球教育展望，2020（5）：119-128.

（1.浙江省溫州市實驗小學? ?325000? ?2.清華大學附屬中學朝陽學校? ?100027）