“六性”：讓復習題撬動學生的數學思維

郭紅敏

[摘 ?要] 有效的復習題不僅可以幫助學生鞏固數學知識和技能，還可以有效發展學生的數學思維，提升學生的數學思維品質。文章從復習題的“自主性”“針對性”“綜合性”“開放性”“遷移性”“文化性”這幾個方面，探討其與數學思維發展之間的關系。

[關鍵詞] 復習題;數學思維;六性;整理與復習

數學習題是鞏固所學知識，形成基本技能，提高解決問題能力，發展數學思維，溝通數學與生活的聯系，培養數學情感的重要途徑。在人教版六年級下冊的“整理與復習”教學中，如何讓學生落實“四基”且有效發展和提高“四能”？復習題的設計和甄選尤為重要。本文從習題設計原則與學生思維發展之間的緊密聯系探討如何設計習題讓學生的數學思維得到發展。

[?] 一、自主性復習題，讓思維更具批判性

自主性是指學生按自己的意愿行事的動機、能力或特性。在教學“整理與復習”時，設計的復習題要能引起學生自主探究、自主參與的強烈意愿，在已有的認知水平上找到新的生長點，將知識點有機地串聯起來，形成新的數學活動經驗，讓學生自主思考，產生新的想法，提出疑問，讓學生的批判性思維得到發展，讓學習真正發生。如復習平面圖形時，筆者給出問題：在長為12.4cm，寬為7.2cm的長方形紙中，剪半徑是1cm的圓，能剪多少個？畫一畫，剪一剪。（人教版六年級下冊第90頁第7題）

學生通過畫一畫、剪一剪等操作活動發現：在長方形里剪出固定大小的圓，不能直接用長方形面積除以圓面積得出可剪圓的個數。由于有長方形面積計算公式推導的活動經驗，學生會想到方中圓，正方形的邊長即圓的直徑，長方形的長有幾個正方形邊長，就表示一排可以剪幾個圓;長方形的寬有幾個正方形邊長，就表示可以剪幾排。學生最終通過計算發現：12.4÷2=6（個）……0.4cm，7.2÷2=3（行）……1.2cm。一排可以剪6個，有3排，利用這樣的剪法，可以剪6×3=18個，如圖1。

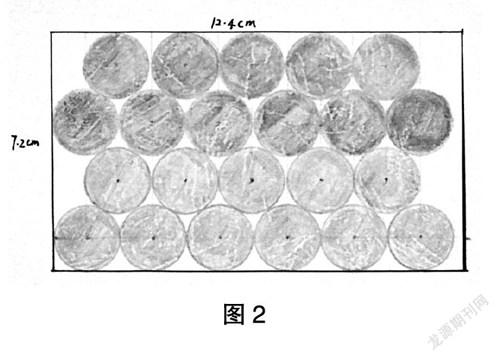
自主性的復習題給了學生思維的活動空間、方法的分享空間。學生在交流中碰撞經驗，于是就會產生疑問：如果圓與圓交錯相拼，會不會擺放更多的圓？問題是讓學習真實發生的內驅力，學生主動參與解決問題，通過再一次的畫一畫、剪一剪等實踐操作，可以體會到圓與圓之間兩兩相切拼擺后不同的結果：第一行剪6個，第二行剪5個，剪出4行這樣的圓，共有6+5+6+5=22個，如圖2。

[?] 二、針對性復習題，讓思維更深刻

針對性是指在復習過程中，根據學生知識儲備的差異，從教材和學生的實際出發，設計適合學生發展的學習內容。在教學“整理與復習”時需要因材施教，既要顧慮班級里大部分學生的學習情況，又要滿足小部分學生的學習需求，所以設計復習題要做到“三針對”：

1. 針對不同層次的學生

通過作業反饋等方式了解全體學生及個別學生的知識儲備情況。習題要由淺入深，由易到難，循序漸進，讓每一層次的學生都能在關鍵處“練”，在生長點上“習”，讓每一位學生的數學思維能力都能在已有的水平上提升。如復習百分數時出示：商場搞活動，所有服飾類物品一律八折銷售。（1）一套西服原價950元，現在多少錢可以買到？（2）一條連衣裙原價700元，實際買到時節約了多少錢？（3）李阿姨買了一件羊毛衫，省了120元。這件羊毛衫原價應是多少錢？

這是一道典型的百分數應用的練習題，但是卻分成了不同難度的三個小題，各小題的練習目標依次是鞏固“已知一個數，求這個數的百分之幾是多少”“一個數減去它的百分之幾是多少”和“已知一個數減去它的百分之幾后的得數，求這個數”。這樣的題組設計，先是順向思維，鞏固基礎知識，后是逆向思維，提升思考能力，滿足了不同層次學生的練習需求。

2. 針對知識的易混淆處

六年的數學知識細碎繁雜，概念抽象，學生易混淆。但這是復習的重點，具體的操作方法是厘清相關知識的前瞻和后延，針對學生出現的典型錯誤，進行對比練習，讓他們在比較中抓住數學本質，抽絲剝繭般地領悟數學知識所蘊含的思想方法。如復習比和比例時出示：

（1）一項工程，甲完成要5小時，乙完成要4小時，甲、乙兩人的工作效率比是________。

（2）從甲地到乙地，客車要行1/4小時，貨車要行2/3小時，客車與貨車的速度比是________。

由于工作總量一定，工作時間和工作效率成反比，甲、乙兩人的工作時間的比是5∶4，所以甲、乙兩人的工作效率比是4∶5，同理可以解決第（2）題。這樣針對易混淆的知識進行對比練習，易于化濁為清，明晰概念。

3. 針對知識的重難點處

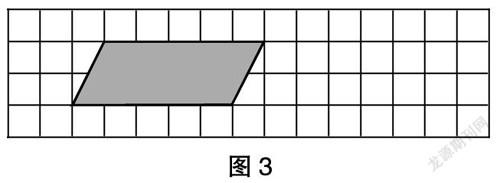
數學知識不是孤立存在的，彼此間既有層次，又有關聯，而重難點知識好比“神經元”，各種細小的基礎知識連起來好比“神經纖維”，只有凸顯出“神經元”，知識網狀的整體性才得以明晰。針對性地復習重難點知識，有利于強化學生對知識的結構性的認識，讓其數學思維變得有序且深刻。如復習平面圖形的面積時出示：如圖3，在方格紙上畫出與給定的平行四邊形面積相等的圖形，你能畫出幾個？你發現了什么？

此題主要溝通不同平面圖形形狀不同、面積相同時底和高之間的關系。學生通過觀察長方形、正方形、三角形、梯形、平行四邊形的面積，從而得出它們都可以用（a+b）h÷2的面積計算公式，進而體會“變中不變”的思想，發展空間觀念。

[?] 三、綜合性復習題，讓思維更靈活

綜合性是指將不同的知識融合在一個情境之中。創設綜合性的復習題，是為了更好地激發學生的求知欲，提高復習的效率，同時讓學生在解決問題中培養思維的靈活性。

1. 數學與實際生活相融合

以現實世界為背景和實際生活問題為引導，帶動知識點的復習，既能解決實際問題，培養學生的數學思維能力，又能激發學習興趣，變枯燥為生動，促進學生的學習可持續發展。如在整理復習“統計與概率”這一相關知識時，教師結合“新冠疫情”來設計復習題：以收集的2020年2月3日—2月13日全國30個省區市和新疆生產建設兵團新冠肺炎新增確診病例數量為例（如圖4，數據來源：國家衛生健康委員會官方網站），要求學生繪制統計圖，分析數據，談發現、說感想和提建議。

學生在經歷統計的過程中，復習了數據的收集、整理和分析的步驟與方法，同時，進一步認識了統計的現實意義，感受了統計與生活的緊密聯系，并能引發對數據變化正確預測的思考。

2. 數學與其他學科相融合

數學不是一門孤立的學科，而應融入各學科組成的大知識之中，所以要關注數學與其他學科的融合，要讓學生善于應用數學和喜歡數學。設計與多學科相融合的復習題，也是增強學生綜合能力的一種手段。如復習體積時出示：怎樣測量一個馬鈴薯的體積？對于不規則物體的體積測量，需要用到轉化的思想，轉化的途徑多樣，用得較多的是物理的方法——排水法。而要利用這一方法測出馬鈴薯的體積，學生需要對實驗程序有一定的統籌與安排。①杯中放入部分水，測量出水的高度h1;②將馬鈴薯完全浸沒于水中，記錄水的高度h2;③用皮尺測量出杯底周長，從而推算出半徑r;④根據水排開的體積就是馬鈴薯的體積，利用V=Sh=πr2（h2-h1），求出其體積。將數學與物理相結合，體會知識間的關聯性，也為學習初中物理利用排水法求相關物體密度等知識積累活動經驗。

3. 數學內部知識間相融合

數學知識間具有逐步遞進的關系，有著一定的合理的認知結構。復習題應注重內部知識間的融合，教師應將一道題精講、講透、講活，由此真正提高復習的效率。比如教學等底等高的長方體、正方體、圓柱和圓錐的體積時，設計復習題：如果圓柱體積是1立方分米，則圓錐的體積是多少？圓錐的底面積是多少？那么，正方體的表面積又是多少？如果圓錐體積要和長方體的體積相等，高度應該怎么變化？要使高度不變，圓錐的底面積又和正方體的底面積成什么關系？同一道題，不同的切入點，就有不同的思維深度。

[?] 四、開放性復習題，讓思維更具獨創性

開放性是指學生不拘泥于單一內容和形式，解決問題時可以有不同的方式，也可以得到不同的答案。復習中，開放的題型以意識的創新為引導，以思維的新度為側重點，以思維的發散為核心。培養學生思維的獨創性，大致分為以下三類：

1. 條件開放，一題多變，培養舉一反三的能力

通過改變條件，題型變得接近卻又不盡相同，學生在變式中厘清概念，追本溯源，能夠有效克服定式思維的負遷移，從而培養舉一反三的能力。

題1 ?一根繩子被剪成兩段，第一段長米，第二段占全長的，這兩段繩子相比（ ? ?）。

A. 第一段長 B. 第二段長

C. 一樣長 D. 無法比較

題2 ?兩根同樣長的繩子，第一根剪去它的米，第二根剪去它的，剩下的兩段繩子相比（ ? ?）。

A. 第一段長 B. 第二段長

C. 一樣長 D. 無法比較

類似的情境，數據相同，求解時都需要真正去理解單位“1”的含義。學生只有通過變化個別條件，進行對比練習，才能做出正確的選擇。

2. 方法開放，一題多解，培養發散變通的能力

方法的開放可以理解為解決問題的多元化，多元化并不是形式的多元，而是新思路、新視角的多元。但是有時并不是思路越多樣越好，而是應在“優化”的前提下，重視方法間的比較，引導“多元化”的達成，這才是思維發散變通的本質。

如數學書90頁的第11題：把一個棱長6cm的正方體切成棱長2cm的小正方體，可以得到多少個小正方體？它們的表面積之和比原來大正方體的表面積增加了多少？

對于第二問，學生思考時借助畫圖來直觀分析題意，從而理出不同的解題思路：可以是先求出所有小正方體的表面積之和，再減去原來大正方體的表面積;也可以是直接求出大正方體被切割后增加的表面積，沿著長、寬、高三個方向各切2次，一共就切了6次，每切一次就增加2個大正方形的面積，也就總共增加了6×2=12個大正方形的面積。

3. 結論開放，多題一解，培養概括歸納的能力

一題可以有不同結論，當然，多題也可以有同一結論。結論的開放，需要學生在各種數學現象中“撥云見日”，梳理出關聯性，分離出問題核心，區分出相同本質。

題3 ?擺一擺，找規律。

（1）用小棒擺三角形，按照圖5擺放的規律，每多搭1個三角形就要增加多少根小棒？

（2）擺第7個圖形需要用多少根小棒？

（3）擺第n個圖形需要用多少根小棒？

在觀察比較中，學生會發現小棒根數與三角形個數之間的關系：以第1根小棒數為基準，添上2根，就成為一個三角形，再添2根，就再增加1個三角形，那么，新增n個三角形需要增加2n根小棒，加上基準的1根小棒，便是2n+1，所以擺第n個圖形需要用2n+1根小棒。

當然，這樣的結論也適用于擺正方形：用火柴按照圖6的方法擺正方形（每條邊擺1根火柴），照這樣，擺15個正方形共需要（ ? ）根火柴。

A. 45 ? ? B. 46 ? ? C. 60

不管是三角形，還是正方形，抑或是五邊形，其實都是“新瓶裝舊酒”，學生在這樣的開放式題目中，一一試錯，一一提煉，一一厘清，在特殊中找到一般，從具體中抽象出模型，進而培養概括歸納的能力。

[?] 五、遷移性復習題，讓思維更敏捷

遷移性可以理解為學生已獲得的知識經驗對完成其他學習活動產生的影響。如果復習時，學生的練習沒有得到層層推進，沒有發生知識遷移，那么學生的獲得也只能夠停留在知識層面，不能夠有思維的提升，也難有活動經驗的積累。

“用一根長24cm的鐵絲圍一個長方體（或正方體）框架。在這個長方體（或正方體）的表面糊一層紙，怎樣用紙最多？”

此復習題是關于已知立體圖形的總棱長求此立體圖形的最大面積的問題。此復習題對學生來說有一定難度，只有遷移到更為低階的知識或方法，才能更好地理解此問題的解決方法。

解決前，可通過厘清兩個知識點來實現方法的遷移，一是周長相等時，長方形與正方形相比，正方形的面積最大;二是底面周長和高相等時，長方體與正方體相比，正方體的體積最大。由這兩個稍微低階的問題，類比遷移來解決此復習題，學生便能理解總棱長一定的長方體與正方體相比，正方體的表面積最大，其表面糊一層紙的紙量也最多。在這里，教師要告知學生正方體是特殊的長方體。

[?] 六、文化性復習題，讓思維更廣闊

文化性凸顯數學的精神、思想及方法的形成和發展。學生通過涉獵具有數學文化性的復習題，不僅能理解數學內涵，還能了解數學在人類文明發展中的重要性，在開闊數學視野的同時培養思維的廣闊性。

比如，在我國古代，隨著農業的發展，各種谷倉、糧庫容積的計算也益加繁重，到《九章算術》成書時代，我國的各種幾何體體積公式都已具備，如計算堆積的方法，以編成歌訣的形式在古代民間廣泛應用：尖堆法用三十六，倚壁須分十八停。內角聚時如九一，外角三九甚分明。

每一句表達一種形式的堆積公式。比如第一句的意思：糧食堆積在平地上成圓錐體，其體積為底面周長的平方乘高，再除以36，即平地堆積=C2h。

試根據上面的平地堆積公式求下面圓錐的體積：一個圓錐形沙堆的底面周長是6米，高是2米，它的體積是多少？

“解題不單單是為了找到答案，應當學會這樣一種對待習題的態度，即把習題看作精密研究的對象，而把解答習題看作設計和發明的目標。” 衡量數學習題質量的一個重要標準就是所設計的習題是否能充分引起學生思考，使學生在鞏固知識的同時，思維也得到發展。總之，復習題把握住自主性、針對性、綜合性、開放性、遷移性和文化性，有助于學生在現實生活中找尋到數學的影子，點燃探索的好奇火種，用數學的理性角度去思考問題，認識世界，并在解決問題中，讓思維“活”起來。