初中數學函數應用題的解題對策研究

摘 要：函數知識是初中數學教學重要的內容，同時也是中考數學試卷常見的題型.但函數知識對初中生而言比較抽象，學習起來存在著一定的困難，無法扎實掌握函數題的解題思路和技巧，同時也會有一些畏懼心理，從而影響到中考試卷中函數應用題的解答和后續高中函數的學習，但二次函數的學習有利于培養學生的思維能力.因此，初中數學教師必須采取有效的措施，讓學生掌握函數應用題解答的思路和技巧，消除畏懼心理.本文對此進行了分析探究，希望能為廣大同仁的函數教學提供參考.

關鍵詞：初中數學;函數的應用;解題對策

中圖分類號：G632 ? 文獻標識碼：A ? 文章編號：1008-0333（2022）08-0044-03

收稿日期：2021-12-15

作者簡介：程曦（1988.2-），女，浙江省杭州人，本科，中學二級教師，從事初中數學教學研究.

函數知識是初中數學學習重要的內容之一，在課程中占據著很大的份額，同時也是中考數學中重要的題型，占據著較大比重的分值.因此，作為初中一線數學教師，必須做好初中函數應用題的分析和研究工作，幫助學生認識到函數知識學習的重要性，傳授學生解題的對策，培養他們解題的思維，提升他們解題的能力，理解并掌握研究函數的學習方法，從而構建高效課堂，并為學生的中考提供幫助，為后續函數的學習提供方法.

根據筆者多年的教學經驗，中考考題年年變，但基本上都是換湯不換藥.作為初中數學教師，我們要贏在課堂教學中，提高課堂效率，認真分析函數應用題的知識點，并將其貫徹到中考當中.基于此，筆者認為初中數學教師應從如下幾個方面著手.

1 把握知識體系，明確題目要求

在初中數學教學中，教師要想傳授學生函數應用題的解題思路和技巧，首先應引導學生把握知識體系，明確題目的要求，提煉題目的有效信息.用通俗的話講就是讓學生讀懂題目，這也是提升學生函數應用題解題技巧和能力的前提基礎.在浙教版初中數學教材中，函數知識主要分為一次函數、反比例函數和二次函數三種類型，其中，二次函數是中考數學試卷必出的題型，且在總分值中占比較大.為了提高學生二次函數解題的準確率，教師在講解函數應用題的過程中，就必須先引導學生把握函數知識的整體脈絡，提升自身的讀題能力，讓他們能夠快速抓住問題的題干和題眼，明確自己要解決的問題是什么，這樣才能幫助學生快速找到解題的思路和方法，準確解決問題.在具體操作中，教師應結合中考的考點和要求，幫助學生理清題目中要考查的知識點是什么，然后能根據解析式找到特殊點，利用描點法畫出二次函數的圖像，根據圖像分析題目中隱含的信息，為解決問題做準備.

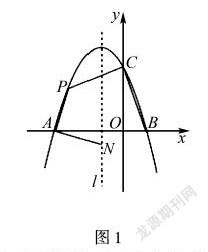
例如：如圖1所示，拋物線y=ax2+bx+c與x軸相交于點A和點B（2，0），與y軸相交于點C（0，6），其對稱軸l為x=-2.

（1）求二次函數的解析式和其頂點的坐標.

（2）如果動點N在對稱軸l上，動點P在第二象限內的拋物線上，①當PA=NA，PA⊥NA時，求此時點P的坐標;②當四邊形PABC的面積最大時，求四邊形PABC的面積最大值及此時點P的坐標.

在講解這道應用題時，教師應巧妙運用轉化思想，將復雜的問題向簡單化的問題轉化，讓學生對該問題熟悉起來，這樣才能讀懂問題，在本題中，可以將點的坐標轉化為線段的長度，再把線段的長度轉化為方程式，把面積最大值的問題轉化為底邊（線段）的最大值問題，這樣才能簡化問題并讀懂問題，從而快速、高效、準確地解答問題，并掌握相應題型的解答規律，這樣才能為中考函數應用題的解題提供幫助.

2 把握解題細節，進行類比分析

在對函數應用題進行解答時，把握解題的細節，并巧妙進行類比分析是解答函數應用題時一個十分重要的技巧和方法.常用的類比分析就是指在解題的過程中，引導學生回顧與該題型相似的題目，然后探尋二者之間的聯系，根據類型模擬曾經的解題方法，從而快速解決問題.在實際教學中，這種解題方法通常也被稱為“變式訓練”，能達到舉一反三的教學效果.但要想運用好這種解題方法，初中數學教師還必須引導學生細致分析該類型題目解題的思路，把握解題的細節，了解應注意的事項，如函數自變量的取值范圍、函數的值域等，切不能一味生搬硬套，導致解題錯誤.

例如，在教學浙教版初中數學九年級上冊第一章《二次函數》第三節《二次函數的性質》的內容時，作業部分第6題：籃球運動員投籃后，籃球運動的路線為拋物線的一部分，拋物線的對稱軸為直線x=2.5，求（1）球運動路線的函數表達式和自變量的取值范圍;（2）球在運動中離地面的最大高度.

在講解這道題時，教師就可以引導學生回顧上一節數學課作業題中的第5題，運動員推鉛球的問題，回想教師在講解這一道題解題的思路和方法，然后把握解題的細節，根據題目給出的數據，并結合教材給出的圖示，設出未知量，并找到等量關系，求出拋物線的方程式，最后再求出未知量.

3 巧用轉化思維，實現數量轉換

初中學生在解答函數應用題時，往往會因為思路不清或者是對未知的參數理解錯誤導致解答錯誤，時間一長，就會打擊到他們學習的積極性和自信心，這樣到了中考時，面對函數問題，就會影響到他們實力的發揮，進而影響到中考答題.面對這一問題，初中數學教師應加強對學生的指導和點撥，引導他們巧用轉化思維，實現數量關系的轉換，如運用逆向思維進行思考，將未知的參數變成已知數，把變量當作常量，通過這樣的數量轉換，降低解題的難度，正確解答函數問題，逐漸培養學生學習的自信心，豐富他們解題的技巧，提升他們解題的能力.

例如：已知x1和x2是關于x的方程（x-2）（x-m）=（t-2）（t-m）的兩個實數根.（1）求x1和x2的值;（2）若x1和x2分別是某直角三角形中兩直角邊的邊長，當實數m和t滿足什么條件時，該直角三角形的面積最大？求出其最大值.gzslib202204031106

在引導學生解答這道函數應用題時，如果學生們直接入手分析實數m和t，幾乎是無法進行解答的，只會讓他們陷入思維混亂當中，從而影響到答題的準確性.數學教師可以引導學生，將問題中的實數m和t當成常量，可以以其中的一個常量對x進行求解，找出x與實數m和t之間的關系式.

4 利用函數圖像，做到數形結合

在初中函數應用題解答時，教師還可以巧妙利用函數圖像，引導學生進行數形結合，這也是提升學生解題能力，將函數問題解答落實到中考當中的有效措施.在實際應用中，利用函數圖像，做到數形結合，能有效降低函數應用題解題的難度，幫助學生更快、更準確地解答出正確的答案.

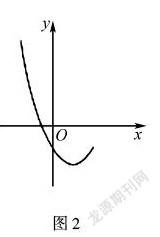
例如，已知拋物線y=x2-2x+c的部分圖象如圖2所示.

（1）求c的取值范圍;

（2）若拋物線經過點（0，-1），試確定拋物線y=x2-2x+c的解析式.

這道函數應用題就是一道典型的蘊含著數形結合思想的題目，在解答這道題時，需要學生在解題的過程中，認真審視題目中所給出的數據及圖像，細心把握住圖像給出的信息及其囊括的相應知識點，然后認真分析，運用數形結合的思想，解答出每一個未知的參數.此外，教師還要引導學生在解出答案后，回過頭來對題目所給的圖像再一次進行分析，細心排除掉圖像中不可能存在的情況，從而提高自己的答題準確率.只有這樣做好數形結合，才能真正有效提升學生的解題能力，為他們中考取得高分奠定基礎.

5 巧用幾何畫板，建立動態思維

與以往的教學相比，幾何畫板可以使原來靜態的函數圖像動起來，從而能夠給學生更加直觀的了解到二次函數的解析式與函數圖像之間的對應關系.例如，在學習圖像變換的相關內容時，教師可以利用幾何畫板動態展示二次函數y=2x2圖像到y=2x+12+4圖像的變化，而在以往的函數教學中，教師通常的做法只能是在黑板上畫出靜態的函數圖像，然后讓學生進行觀察比較，但往往人工作圖會出現誤差，不太標準的圖形很難收到理想的教學效果.在二次函數的教學中，幾何畫板還能進一步對所學知識進行更深入的探究，輔助學生對二次函數性質的理解和歸納，幾何畫板中的移動、計算、隱藏、系列等功能，能使教學活動更加生動形象，學生的數學理解力更強，教學效率更高，同時，學生有了動態圖的直觀感受后對題目的分析也會更全面，從而加深對函數的理解，提高解決函數問題的能力.

綜上所述，在初中數學教學中，函數知識是教學中重要的內容，也是中考數學試卷必出的題型.在實際教學中，函數知識的內容比較豐富，解答起來具有一定的難度.作為初中數學教師，應在日常的教學中想方設法將其落實到中考中，結合中考的要求，讓現代信息技術作為輔助手段，教會學生找等量關系，提取題目中的隱含信息，然后再通過對其他條件的分析，提高學生解題和分析的能力，從而為學生的全面發展奠定堅實的基礎，同時也為后續的更復雜的函數學習做好準備.

參考文獻：

[1] 魏雪梅.初中數學函數應用題的解法探究[J].中學數學，2020，614（16）：57-58.

[2] 張小亮.初中數學課堂教學中數形結合思想在函數解題中的應用探究[J].新課程（中），2019，470（01）：41-41.

[3] 黃林斌.初中數學函數應用題解題教學分析[J].高考，2018，300（29）：201.

[4] 鄒迎春.初中數學函數應用題解題教學略談[J].吉林教育，2017，839（39）：49-50.

[5] 黃端鑫.例談初中數學有關三角函數應用題的四個模型[J].中學數學研究（華南師范大學版），2017，423（06）：41-42.

[6] 張運虎.有關函數的綜合應用題解析[J].語數外學習（初中版），2017，559（03）：30-33.