關(guān)于數(shù)學(xué)符號感及其發(fā)展策略的探究

劉 梅，李占峰

(周口師范學(xué)院 a.數(shù)學(xué)與統(tǒng)計學(xué)院；b.教務(wù)處，河南 周口 466001)

符號是從具體事物和情景中抽象概括出的一種簡明記號，用來交流、推理、計算和解決問題的工具[1]。從某種意義上來說，人們生活在“符號化”的世界里，由于符號和符號體系的出現(xiàn)，數(shù)學(xué)才能以簡潔明了、結(jié)構(gòu)優(yōu)美的形式出現(xiàn)，它對數(shù)學(xué)發(fā)展的推動作用是非常大的。德國著名數(shù)學(xué)家萊布尼茨說：“符號的巧妙和符號的藝術(shù)是人們絕妙的助手，因為它們使思考工作得到節(jié)約，在這里它以驚人的形式節(jié)省了思維。”[2]杰出的俄國數(shù)學(xué)家羅巴切夫斯基說：“數(shù)學(xué)語言更加完善、準(zhǔn)確明了地提供了把一些概念傳達給別人的方法。利用符號，數(shù)學(xué)上的每一個論斷和它所描述的東西就可以更快地被別人所了解。”[3]

數(shù)學(xué)符號感是對符號模式和符號關(guān)系的意識，并用這種意識靈活解決數(shù)學(xué)問題的能力[4]。數(shù)學(xué)符號是數(shù)學(xué)語言的基本成分，伴隨著人類文明的發(fā)展而快速發(fā)展，是數(shù)學(xué)交流、數(shù)學(xué)思考、數(shù)學(xué)表達的重要工具。用符號來表示數(shù)的過程是人們表示和認(rèn)識研究對象的開始，是深入探索數(shù)的關(guān)系、事實、性質(zhì)及數(shù)學(xué)模式的必然發(fā)展。數(shù)學(xué)符號和特定的對象相聯(lián)系，和概念的本質(zhì)特征緊密相關(guān)，正確掌握和運用符號可以提高人們的抽象概括能力。數(shù)學(xué)中的邏輯推理關(guān)系就在于能夠合理、恰當(dāng)?shù)剡\用符號，而這卻要依賴于人們在長期的學(xué)習(xí)符號、創(chuàng)造符號、理解符號、應(yīng)用符號的時候培養(yǎng)和發(fā)展起來的數(shù)學(xué)符號感的引導(dǎo)作用[5]。在解決實際問題時，《全日制義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn) (實驗稿)》(以下簡稱《標(biāo)準(zhǔn)》)根據(jù)數(shù)學(xué)課程和學(xué)科的特點，得出義務(wù)教育階段一個非常重要的學(xué)習(xí)內(nèi)容是在具體問題中培養(yǎng)學(xué)生的數(shù)學(xué)符號感。

一、數(shù)學(xué)符號的發(fā)展歷史

數(shù)學(xué)符號一般分為以下幾種：

(1)數(shù)量符號：如 5、3+2i、e、π、∞等。

(2)運算符號：如加、減、乘、除(+、-、×、÷)，比(∶)等。

(3)關(guān)系符號：如“=”是相等的意思、“≈”為近似等號、“≠”是不等號，還有“<”(小于號)、“>”(大于號)、“‖”(平行符號)、“⊥”(垂直符號)等。

(4)結(jié)合符號：如花括號{ }、方括號[ ]、圓括號( )等。

(5)性質(zhì)符號：如絕對值符號(| |)、正負(fù)號(±)等。

(6)簡寫符號：如三角形(△)、因為(∵)、所以(∴)、階乘(！)、總和(∑)等。

所有數(shù)學(xué)符號都是經(jīng)過長期演變、發(fā)展而形成的，了解這些符號產(chǎn)生和發(fā)展的歷史過程，能夠讓人們領(lǐng)略數(shù)學(xué)符號的美學(xué)價值，感受符號化思想方法和數(shù)學(xué)文化。

二、數(shù)學(xué)符號感的表現(xiàn)

符號感是自覺地、主動地運用符號和理解符號的意識[6]與態(tài)度，不同的人對于符號感的看法則有不同。對符號感的理解包括：理解數(shù)學(xué)符號表示的意思，會使用這些符號；領(lǐng)會數(shù)學(xué)符號的意義與作用，知道使用這些符號的益處；在學(xué)習(xí)符號和應(yīng)用符號時，在與人交流和獨立思考時，能主動地、經(jīng)常地，甚至是創(chuàng)造性地使用符號。有人認(rèn)為從語言和認(rèn)知的角度來講，數(shù)學(xué)符號感是人們在數(shù)學(xué)的語言環(huán)境中，對數(shù)學(xué)符號及數(shù)學(xué)問題本質(zhì)特征的快速、敏捷反應(yīng)。主要表現(xiàn)在面對數(shù)學(xué)符號和數(shù)學(xué)關(guān)系式時，能夠準(zhǔn)確地理解數(shù)學(xué)符號的真實含義，揭示出關(guān)系式中所蘊含的客觀規(guī)律；面對與數(shù)學(xué)有關(guān)的實際問題時，能夠迅速地使用符號，從中抽象出數(shù)學(xué)模型。而《標(biāo)準(zhǔn)》明確強調(diào)：“發(fā)展學(xué)生的符號感就是能從具體問題中使學(xué)生能夠抽象出變化規(guī)律和數(shù)量關(guān)系，會用數(shù)學(xué)符號表示；深刻理解數(shù)學(xué)符號所表示的數(shù)量關(guān)系，并進行符號間的變換；對于用數(shù)學(xué)符號所表示的問題能選擇合適的方法解決。”

1.在具體情境中抽象出變化規(guī)律和數(shù)量關(guān)系，并用符號表示

用數(shù)學(xué)符號來表示變量間的變化規(guī)律和數(shù)量關(guān)系的基礎(chǔ)是引進字母表示[6]。荷蘭數(shù)學(xué)家弗賴登塔爾表示，“用字母表示數(shù)學(xué)符號的作用：字母作為專用名詞，在特定集合中使用專用名詞；字母作為非專用名詞，可以用日常中的‘人’來表示所有的人”。

在數(shù)學(xué)語言中，描述各種實際問題的基礎(chǔ)是數(shù)字、字母、符號。學(xué)生認(rèn)識上的飛躍是從研究數(shù)到研究用字母表示數(shù)，但是學(xué)生在初學(xué)時總是感到非常困難，有些學(xué)生基本是機械地記憶，根本不清楚符號的真正意義。因此，在實際問題中教師要盡量引入數(shù)學(xué)符號，這樣可以讓學(xué)生更容易理解用字母表示一般數(shù)的實際意思。

(1)用字母表示計算公式、運算法則以及運算規(guī)律。此表示方法最初是從小學(xué)數(shù)學(xué)中數(shù)的運算開始接觸的。

(2)用字母表示學(xué)科和實際問題中的數(shù)量關(guān)系。

(3)用字母代表數(shù)，方便在實際問題中抽象出變量關(guān)系、變化規(guī)律，進而可以用相關(guān)的數(shù)學(xué)知識去解決與實際相聯(lián)系的問題[7]。

關(guān)于《標(biāo)準(zhǔn)》中說的“在實際問題中抽象出變化規(guī)律和數(shù)量關(guān)系，會用符號表示”的意義在于，這種表示方法一般開始于發(fā)現(xiàn)和探索規(guī)律，再用代數(shù)式將它們一般化地表示出來。一般化超越了實際問題情境，深刻指明和揭示問題中的普遍性和共性，從而把推理和認(rèn)識推向更高水平[8]。

2.理解符號表示的變化規(guī)律和數(shù)量關(guān)系

(1)從實際問題中能夠深刻理解數(shù)學(xué)符號代表的意義和關(guān)系式代表的意義。

(2)用圖像、表格、關(guān)系式表示變量間隱含的關(guān)系。

(3)從圖像、表格、關(guān)系式表示的變量關(guān)系中得到需要的信息。

3.會進行符號間的轉(zhuǎn)換

用數(shù)學(xué)符號所表示的變量關(guān)系的變換主要是指解析式法、表格法、語言表示和圖像法之間的變換。

深入理解問題背景或概念本身的有效方式是呈現(xiàn)和描述數(shù)學(xué)對象，因此，對于單一對象掌握更多的表示方法，有助于強化對概念的深入理解。分析學(xué)習(xí)數(shù)學(xué)心理可知，學(xué)習(xí)數(shù)學(xué)的核心是不同的表達方式及其思維形式之間的轉(zhuǎn)換。把變量關(guān)系從一種形式轉(zhuǎn)換成另一種形式，也就是前面所提及的四種表示形式之間相互轉(zhuǎn)化，這是構(gòu)成學(xué)習(xí)數(shù)學(xué)過程中非常重要的方面[9]。

圖像表示法的直觀性對于深入理解變量間的關(guān)系非常重要，其作用也是其他表達方式不能替代的。圖像表示法是把數(shù)據(jù)、關(guān)系式轉(zhuǎn)變?yōu)閹缀涡问剑裕朔ㄊ悄堋翱匆姟弊兞筷P(guān)系及變化情況的一種方法。

四種表示方法是相互聯(lián)系的，對于同一對象如果一種表示方法發(fā)生了變化，其他表示方法也會相應(yīng)地變化。

4.選擇適當(dāng)?shù)乃惴ń鉀Q問題

將具體問題用數(shù)學(xué)符號表示是解決實際問題的第一步，之后可以選擇合適的算法進行符號之間的運算。簡單來說，解決問題的第一步是把實際問題轉(zhuǎn)化為數(shù)學(xué)問題，然后再運用數(shù)學(xué)理論運算、推理得出結(jié)果，選擇合適的算法以及進行符號運算是十分重要的問題。

三、符號感的發(fā)展策略

1.在實踐活動中發(fā)展數(shù)學(xué)符號感

數(shù)學(xué)符號具有高度的形式化、精確性和概括性特點，這讓學(xué)生感到數(shù)學(xué)符號太抽象、難理解，甚至感到枯燥乏味，從而導(dǎo)致學(xué)生缺乏學(xué)習(xí)興趣，也影響學(xué)生對數(shù)學(xué)符號的理解和符號關(guān)系式的記憶及應(yīng)用。

案例1：若“*”號表示一種運算，且滿足以下兩個條件：(1)1*1=1 (2)(x+1)*1=3(x*1)(x≥1，x∈N+，N+為正整數(shù))，則x*1=( )

A.3x-2 B.3xC.3x+1 D.3x-1

這是一道高中一年級的考題，能夠很好地檢驗學(xué)生的數(shù)學(xué)符號感。針對這一考題筆者對一所重點中學(xué)一年級的學(xué)生進行了訪問調(diào)查，發(fā)現(xiàn)學(xué)生解答的正確率不高。在對一所普通民辦高中二年級一個班80多人的集體訪問調(diào)查時，在3—5分鐘的時間里竟沒有一位學(xué)生正確作答。對初中數(shù)學(xué)教師和大學(xué)本科、專科數(shù)學(xué)系學(xué)生的調(diào)查情況相對好一些，但在3—5分鐘的時間里也只有少數(shù)人能夠正確作答。是什么原因?qū)е逻@樣的情況出現(xiàn)呢？下面的訪談錄可以說明一些問題。

訪談?wù)撸嚎荚囍羞@道題你是如何作答的？

學(xué) 生：看不懂。

訪談?wù)撸侯}設(shè)說的很清楚呀！“*”號表示一種運算，滿足兩條規(guī)律。

學(xué) 生：哪有這種運算呢？

訪談?wù)撸簲?shù)學(xué)中的運算有很多，有些是已經(jīng)學(xué)習(xí)過的，如加、減、乘、除等，還有更多是沒有學(xué)習(xí)過的。“*”號表示的運算就是這種情況，這里的N+表示正整數(shù)，1*1=1題設(shè)已經(jīng)給出，那么對于其他的一些正整數(shù)，它們和1的運算結(jié)果會怎樣呢？(學(xué)生立刻從x=2、3……入手進行運算歸納，片刻得出結(jié)果)。

學(xué) 生：答案應(yīng)該是3x-1，選D，我差一點兒選對。

訪談?wù)撸耗惝?dāng)時是如何想的呢？

學(xué) 生： 我當(dāng)時想1*1=1和乘法運算相似，一個數(shù)連乘就會出現(xiàn)乘方，所以感覺不是選D就是選B，最后選擇了B。

分析以上問答，容易發(fā)現(xiàn)學(xué)生思路受阻的原因在于對“*”號表示運算不理解，不能敏銳地體會出“*”號所表示的運算規(guī)律。雖然學(xué)生對1*1=1有所認(rèn)識，并在此產(chǎn)生了解決問題的數(shù)學(xué)直覺，但由于對(x+1)*1=3(x*1)(x≥1，x∈N+，N+為正整數(shù))所蘊含的規(guī)律缺乏感知，解決問題的數(shù)學(xué)直覺合理性得不到理性的邏輯驗證，最后導(dǎo)致盲目作答。究其根本原因則是學(xué)生對以往所學(xué)習(xí)的有關(guān)運算及其符號表示的本質(zhì)缺乏理解，對符號化過程中所表示的一般化的數(shù)學(xué)思想體會不深。事實上，能夠正確作答的學(xué)生也都是對x=1、2、3等各種特殊情況所得結(jié)果進行歸納得出正確答案的。但這一答案的正確性還需要用數(shù)學(xué)歸納法加以證明，對于高中一年級的學(xué)生，這一點很難做得到。如若對數(shù)學(xué)運算有較深入理解，在此基礎(chǔ)上發(fā)展起來的數(shù)學(xué)符號感就較強，自覺地運用數(shù)學(xué)符號的意識也就強，就能產(chǎn)生更簡捷美妙的方法。

訪談?wù)撸骸?”號表示一種運算，運算就是一種關(guān)系，以往所學(xué)習(xí)的“加、減、乘、除”等運算，實質(zhì)上是兩個元素之間有了某種關(guān)系之后，會有一個新元素和它們對應(yīng)。這里“*”號所表示的運算不也是這樣嗎？

學(xué) 生：(經(jīng)過思考)是的。

訪談?wù)撸耗敲矗隳軐⒁陨蟽蓚€運算關(guān)系式簡化一些嗎？

學(xué) 生：設(shè)ax=x*1，上述關(guān)系式可表示為(1)a1=1，(2)ax+1=3ax(x∈N+)

至此被訪談?wù)哒f：“這不是一個等比數(shù)列嗎？我應(yīng)該想到呢！”

是呀，我怎么就想不到呢？這正是數(shù)學(xué)教學(xué)和數(shù)學(xué)學(xué)習(xí)所應(yīng)思考、研究的問題。

人們的數(shù)學(xué)符號感是在數(shù)學(xué)的實踐活動中發(fā)展起來的，由于人先天素質(zhì)的差別，后天的個人經(jīng)驗不同，數(shù)學(xué)符號感也不相同，表現(xiàn)在數(shù)學(xué)理解上就有層次之分，體現(xiàn)在數(shù)學(xué)思維能力上則有強弱之別。具體到所給案例，許多受訪者坦言，如若給予足夠的考慮，他們會想到從特殊到一般地歸納方法得到答案，但不會想到對所給關(guān)系式進一步抽象，轉(zhuǎn)化為等比數(shù)列的問題來處理。因此，在數(shù)學(xué)的實踐活動中發(fā)展數(shù)學(xué)符號感是非常重要的。

2.在具體情境中發(fā)展數(shù)學(xué)符號感

在已往的經(jīng)驗中，發(fā)展數(shù)學(xué)符號感的基礎(chǔ)是挖掘人們內(nèi)心潛藏的“符號意識”。因此，應(yīng)重視生活中給人們提供的感受和體驗機會，運用“現(xiàn)實生活問題→轉(zhuǎn)化為數(shù)學(xué)問題→用數(shù)學(xué)符號表示”這種將實際問題逐步符號化的方法，鍛煉發(fā)展學(xué)生的數(shù)學(xué)符號感。

案例 2：在確定烤制時間時某烤鴨店的主要依據(jù)，見表1：

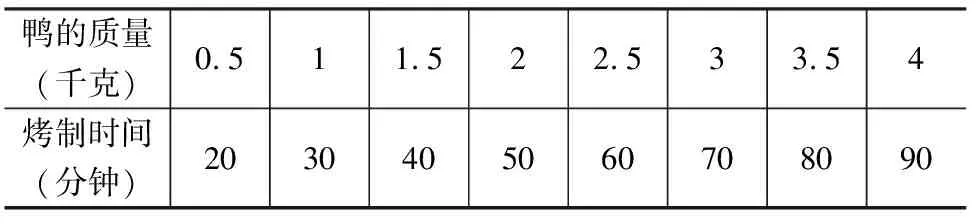
表1 烤鴨質(zhì)量與烤制時間對應(yīng)關(guān)系

利用表1所提供的數(shù)據(jù)可以清晰地看出，鴨的質(zhì)量和所需烤制時間的對應(yīng)關(guān)系。然而，如果需要烤制鴨的質(zhì)量是2.8千克，則需要多長時間呢？面對表格中的兩組數(shù)，學(xué)生發(fā)現(xiàn)鴨的質(zhì)量與烤制時間之間有一個對應(yīng)關(guān)系，這些對應(yīng)關(guān)系的直觀圖形是什么形狀呢？從而產(chǎn)生一種動手操作的想法，通過作圖發(fā)現(xiàn)，這些數(shù)據(jù)所對應(yīng)的點反應(yīng)在圖像上是一條直線，從而對這一問題就有了更深入的理解，即鴨的質(zhì)量與烤制時間具有一次函數(shù)的關(guān)系。從而想到用關(guān)系式來表示鴨的質(zhì)量與烤制時間之間的關(guān)系，用w千克表示鴨的質(zhì)量，用t分鐘表示烤制的時間。通過表格中的數(shù)據(jù)可以得出，鴨的質(zhì)量每增加0.5千克，烤制時間則增加10分鐘，從而得出關(guān)系式：t=20w+10(w>0)，于是也就可以得到烤制2.8千克鴨所需的時間。當(dāng)然，也可以繪制圖像，如圖1。

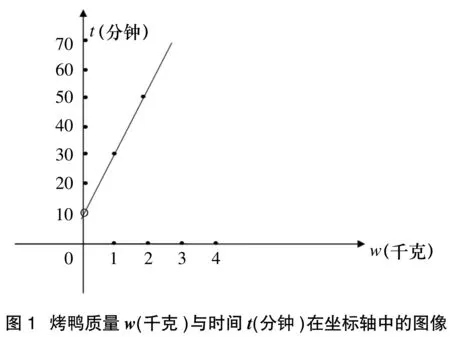
這種由具體數(shù)字到直觀圖形，再由直觀圖形到數(shù)學(xué)關(guān)系式的解題途徑，表明學(xué)生對符號感的認(rèn)識在逐步深入。由此也說明培養(yǎng)學(xué)生符號感的一個重要途徑是在具體問題中發(fā)展數(shù)學(xué)符號感。

3.在解決實際問題中發(fā)展數(shù)學(xué)符號感

在解決實際問題中，教師應(yīng)當(dāng)在學(xué)生深刻領(lǐng)會數(shù)學(xué)符號、數(shù)學(xué)表達式、數(shù)學(xué)關(guān)系式含義的基礎(chǔ)上，培養(yǎng)發(fā)展數(shù)學(xué)符號感，避免造成學(xué)生對符號演算的機械記憶，應(yīng)多增加與符號有關(guān)的實際背景、幾何解釋、探索過程等內(nèi)容，從而幫助學(xué)生深入理解。

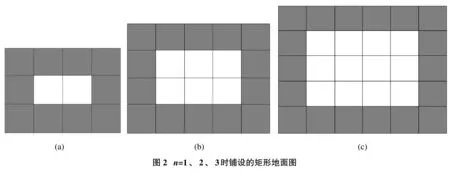
案例3：如圖2，用型號相同的黑白兩種顏色正方形地板磚鋪設(shè)矩形地面，根據(jù)所給圖形回答以下問題：

(1)考察在第n個距形圖中，每一橫行各有____塊地板磚，每一豎列各有____塊地板磚。(請用含n的表達式表示，n∈N+)

(2)設(shè)鋪設(shè)矩形地面所用地板磚的總數(shù)為y塊，請給出變量y與(1)中的變量n的函數(shù)表達式。

(3)按照上述的鋪設(shè)辦法，如果鋪一塊矩形地面共用506塊地板磚，請求出n的值。

(4)若黑色地板磚的單價是4元，白色地板磚的單價是3元，在上述問題(3)中，購買這樣的地板磚共需花多少元錢？

(5)請通過計算說明是否存在所用黑色地板磚與白色地板磚塊數(shù)相等的時候？

通過觀察，歸納出每一橫行各有n+3塊地板磚，每一豎列各有n+2塊地板磚，從而求出總塊數(shù)y與n的函數(shù)關(guān)系式為y=(n+3)(n+2)=n2+5n+6。根據(jù)已知的函數(shù)值y=506可以求出自變量n的值為20。通過計算可得第n個圖形黑色地板磚的數(shù)量為4n+6塊，白色地板磚的數(shù)量為n2+n塊。當(dāng)n=20時可計算出黑色地板磚的數(shù)量為86塊，白色地板磚的數(shù)量為420塊，所以共需花費1 604元錢。最后根據(jù)解一元二次方程n2+n=4n+6，得出n的值不是正整數(shù)，與實際情況不符，所以，黑色地板磚與白色地板磚塊數(shù)相等的時候是不存在的。

符號是數(shù)學(xué)的語言，數(shù)學(xué)語言系統(tǒng)是被符號化的系統(tǒng)，難以想象如果當(dāng)今數(shù)學(xué)沒有精確化的符號會變成怎樣。所以，數(shù)學(xué)學(xué)習(xí)的一大特色是用符號表示數(shù)學(xué)內(nèi)容和數(shù)學(xué)方法。數(shù)學(xué)語言體系不同于其它語言系統(tǒng)，如英語、漢語、德語等，正因為如此，數(shù)學(xué)語言才更有可能成為一種國際化的通用語言。培養(yǎng)學(xué)生的數(shù)學(xué)符號感，對他們領(lǐng)悟語言的概括美和簡潔美，熏陶他們對數(shù)學(xué)學(xué)習(xí)的興趣，增強其自主學(xué)習(xí)數(shù)學(xué)的積極性是非常必要的。