飛翼無人機著艦橫側向控制律設計

劉光銳，陳欣

(南京航空航天大學，江蘇 南京 210016)

0 引言

飛翼布局無人機擁有氣動和結構效率高、升阻比和有效載荷量大、載荷分布均勻以及隱身性能好等優點[1]，因而受到了世界各國的廣泛關注。目前，這一類無人機在世界范圍內尚未投入使用，還處于試驗階段。

對艦載機而言，影響艦載機著艦的因素有海洋、大氣和著艦平臺等，這些因素導致艦載機的著艦操作異常復雜。據公開資料，美國的X-47B無人機是當前世界上唯一一款成功在航母上自主起降的無人機[2-3]，其著艦方式采取人工控制和自適應控制相互結合。飛翼無人機的研究技術屬于機密，當前理論界的研究成果甚少。王鑫[4]提出基于多變量模型參考自適應理論的抗干擾飛行控制律，在較快的響應下通過抑制作用保證系統的穩態、瞬態響應各項指標的穩定性。楊恩泉等[5]人指出，基于反饋線性化方法的非線性控制方法需要精確的系統模型，然而這是很難做到的。

在飛翼無人機著艦過程中，對理想著艦點的高度與距離的精確跟蹤仍是一大難點。本文首先針對無人機著艦橫向控制提出了幾點要求，并設計了航向增穩控制律，解決了飛翼無人機著艦橫側向荷蘭滾模態不穩定的問題；其次基于自適應動態逆理論設計了滾轉角控制律，使滾轉角控制變得準確、穩定；最后設計了以航跡角控制器和側向速度控制器，實現了平動軌跡的精確跟蹤，同時在每個控制器設計后都對控制器的響應和裕度進行了魯棒性分析驗證。

1 著艦橫側向控制需求

在理想狀態下無人機可無側滑地降落在航母飛行甲板著艦區域內并順利掛上阻素[6]。實際操作中，飛翼無人機將面臨著十分復雜的著艦環境，影響飛機順利著艦。分析可知，飛翼無人機著艦的橫側向控制需滿足以下條件：

1)著艦航向范圍的控制。為防止無人機在著艦后滑向側方，需保證飛行航向與著艦甲板中心線方向一致，無人機的航向與航母飛行甲板的中心線夾角須控制在±3°范圍以內。

2)著艦側偏的控制。在飛翼無人機著艦過程中，需保證無人機理想著艦點控制在相對航母甲板中心線的±3 m距離以內[7]。

3)飛翼無人機航向的增穩控制。由于飛翼無人機的特殊氣動布局，其航向不夠穩定[8]。為保證航向的穩定性，需要設計增穩控制。

4)需要設計抗擾動能力強的橫側向控制律。海平面是一個復雜的著艦環境，在這樣的環境下無人機在著艦過程中會受到大氣擾動和艦尾流[9]等多種不同的擾動。為使無人機可以安全著艦，設計的橫側向控制律應可以很好地克服外來擾動帶來的干擾。

為滿足上文提出的4個控制需求，設計了如圖1所示的無人機著艦橫側向控制結構。

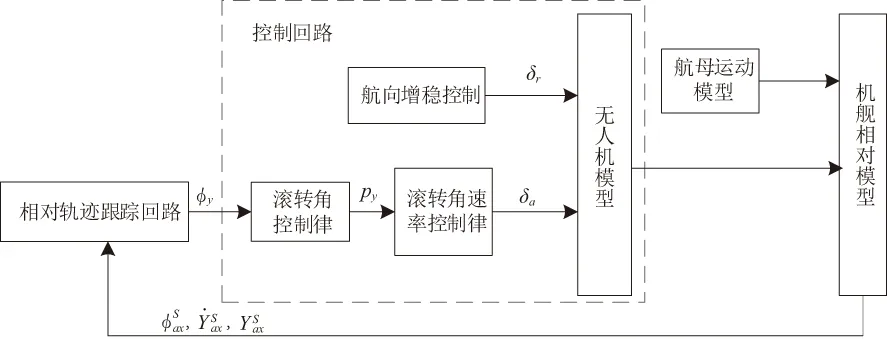
圖1 自動著艦橫側向通道控制結構

2 增穩控制律設計

飛翼無人機縱向模態偏于穩定，但是橫側向模態阻尼較弱。因此應進行增穩控制律的設計，使無人機模態穩定。

為了快速消除側滑角，抑制荷蘭滾模態的發散，需要增強航向靜穩定性。為解決航向阻尼不足問題，文中將側滑角β負反饋加入至方向舵通道，同時再利用改變滾轉角速度來提高航向穩定性，讓無人機模態趨于穩定。因此橫側向的增穩控制律結構為

(1)

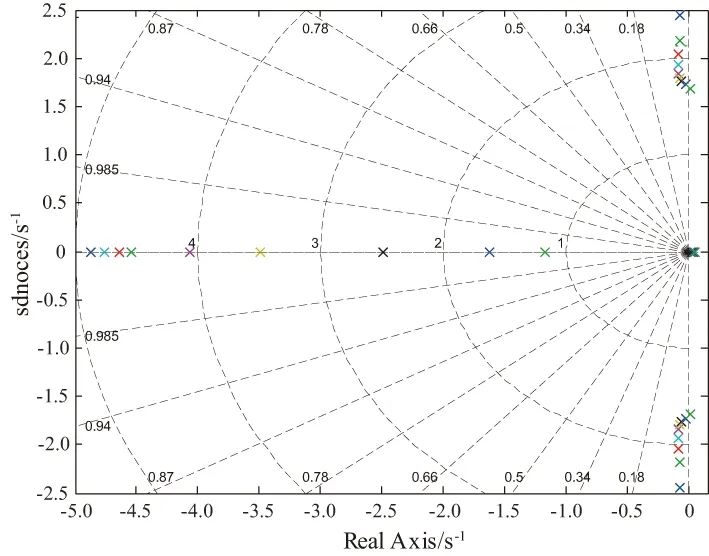
圖2 航向增穩前

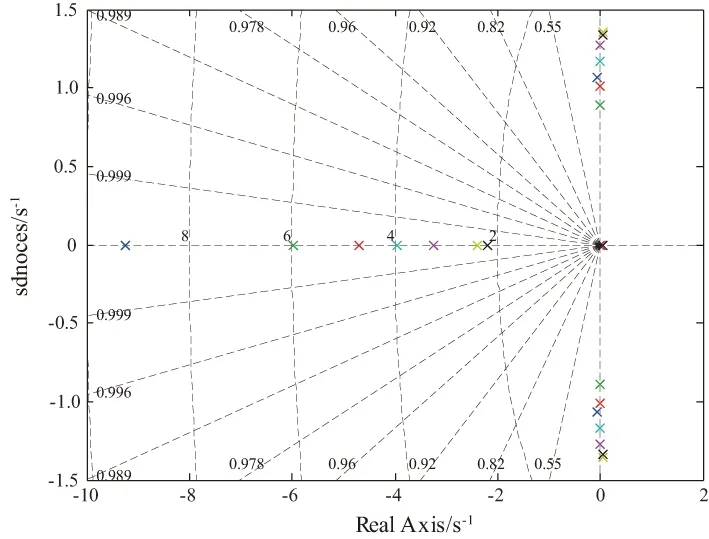
圖3 航向增穩后

3 滾轉角控制律設計

飛翼無人機想要實現橫側向平動軌跡跟蹤，必須在著艦過程中保持滾轉角穩定。為實現無人機迅速、穩定地滾轉，本文采用滾轉角為外環控制、滾轉角速率為內環控制的方式設計滾轉通道控制律。圖4所示為本文設計的滾轉角控制律結構。

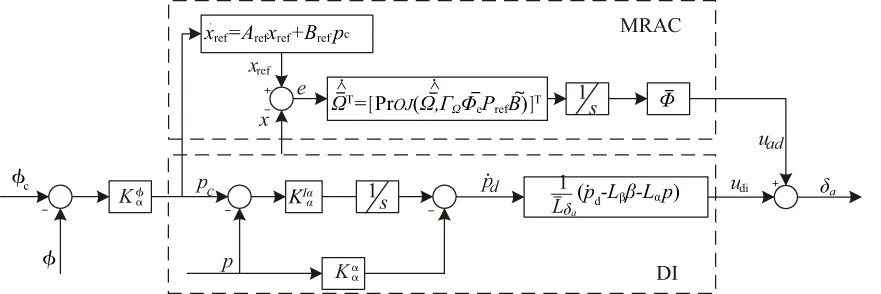
圖4 滾轉角控制律結構

本文對于滾轉通道的控制律采用自適應動態逆理論設計。控制器中指令模型采用2階系統模型，模型為

(2)

(3)

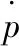
(4)

因此，滾轉角速度動態逆控制律為

(5)

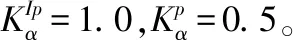
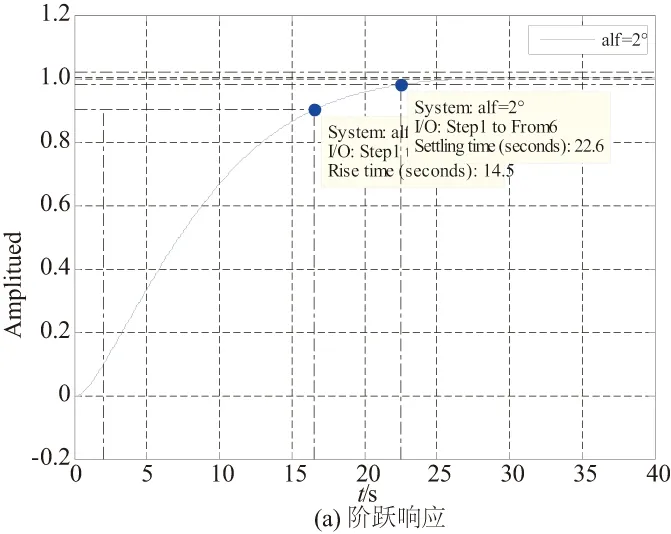
圖5 滾轉角速度階躍響應與開環伯德圖

在滾轉角速率控制器設計的基礎上，基于經典PID控制可設計滾轉角控制律為

(6)

滾轉角速度指令輸入和滾轉角輸出的傳遞函數如下：

(7)

如圖6所示，系統階躍響應無超調，上升時間約為2.18 s，調節時間約為13.5 s，系統無靜差。同時開環傳遞函數的相角裕度約為91.4°，幅值裕度約為38.1 dB，設計點的裕度達到要求。

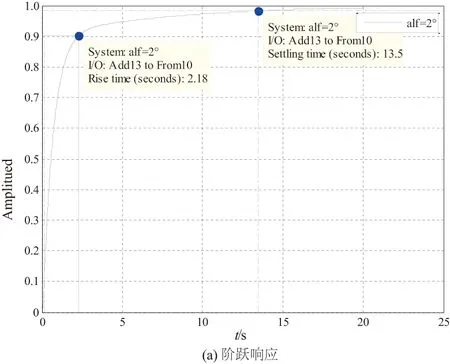
圖6 滾轉角階躍響應與開環伯德圖

4 平動軌跡跟蹤控制律設計

為更好地使無人機實現平軌跡跟蹤，需要將航跡角與艦船中心線對準并消除側向偏差[10]。文中設計了如圖7所示的水平軌跡跟蹤控制律。

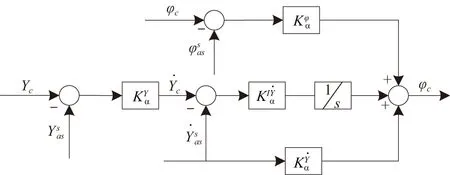
圖7 平動軌跡跟蹤控制律結構

航跡角對準甲板跑道中心線是平動軌跡跟蹤的關鍵。航跡角控制通道是滾轉角控制通道的外回路，故本文在滾轉角控制律的基礎上設計航跡角控制律，可得到滾轉角指令輸入到航跡角輸出的傳遞函數為

(8)

由滾轉角控制律可知，航跡角控制律為

(9)

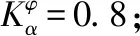
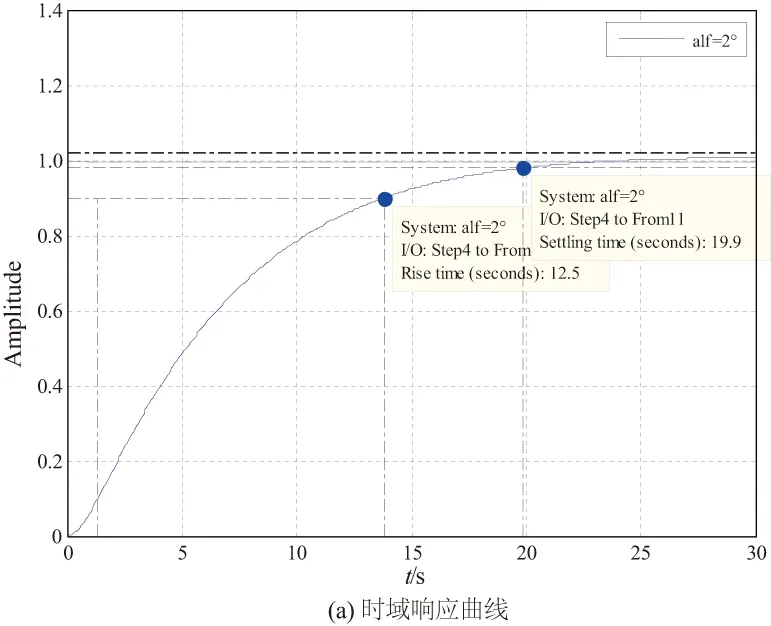
圖8 航跡角時域響應曲線與開環頻域響應圖

航跡角控制器只能使航跡角與甲板跑道中心線對準，但無法消除側向偏差。本文選擇在航跡角控制律的基礎上設計側向速度控制律，通過控制側向速度調整無人機側向位置來消除側偏。

滾轉角指令輸入到相對側向速度輸出的傳遞函數為

(10)

采用比例積分環節設計側向速度控制律，可得控制律為

(11)

在側向速度控制律的基礎上分析可知側向速度指令輸入到側向位置的傳遞函數為

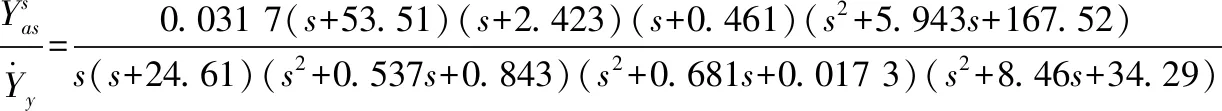
(12)

采用比例控制設計側向位置控制律，可得控制律為

(13)

如圖9所示，系統階躍響應無超調，上升時間約為7.83 s，調節時間約為12.8 s，系統無靜差。開環傳遞函數的相角裕度約為76.4°，幅值裕度約為45.9 dB，設計點的裕度達到要求。如圖10所示，系統階躍響應無超調，上升時間約為21.5 s，調節時間約為38.4 s，系統無靜差。開環傳遞函數的相角裕度約為73°，幅值裕度約為24.1 dB，設計點的裕度達到要求。

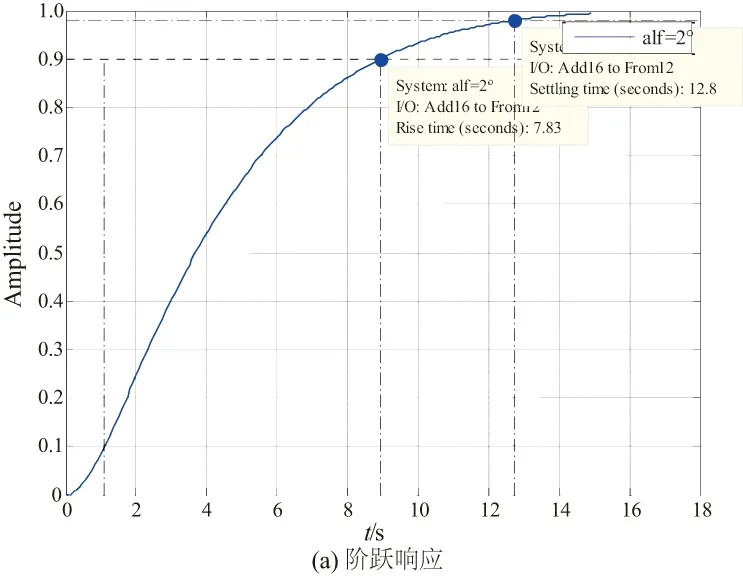
圖9 側向速度階躍響應與開環伯德圖

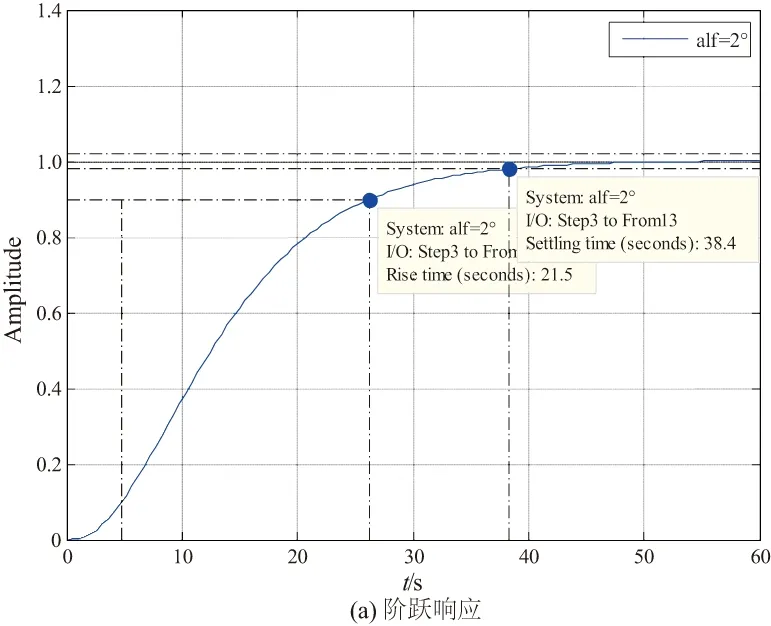
圖10 側向位置階躍響應與開環伯德圖

5 仿真驗證

為了驗證控制器的控制精度及控制效果，如圖11所示，在Matlab/Simulink環境下構建了著艦仿真數值環境，根據仿真環境模型分別對飛翼無人機在平靜大氣環境與有艦尾流擾動的情況下進行著艦仿真。假設艦船以15 m/s的速度勻速前進，樣例無人機在初始高度為120 m，速度為60 m/s，沿-3.5°理想著艦下滑軌跡著艦。

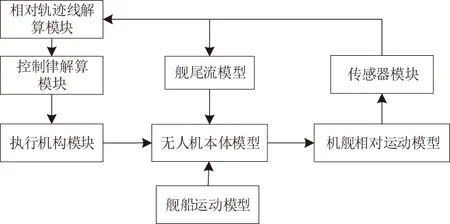
圖11 某型無人機著艦數值仿真環境

1)平靜大氣環境下著艦仿真

由圖12可知，無人機在自動著艦過程中橫側向保持無側滑飛行；同時在過程中保持2 m/s的側向速度跟隨艦船的側向運動；相對艦船甲板跑道中心線的側向偏差最大約0.5 m，實現了無人機無側偏觸艦。

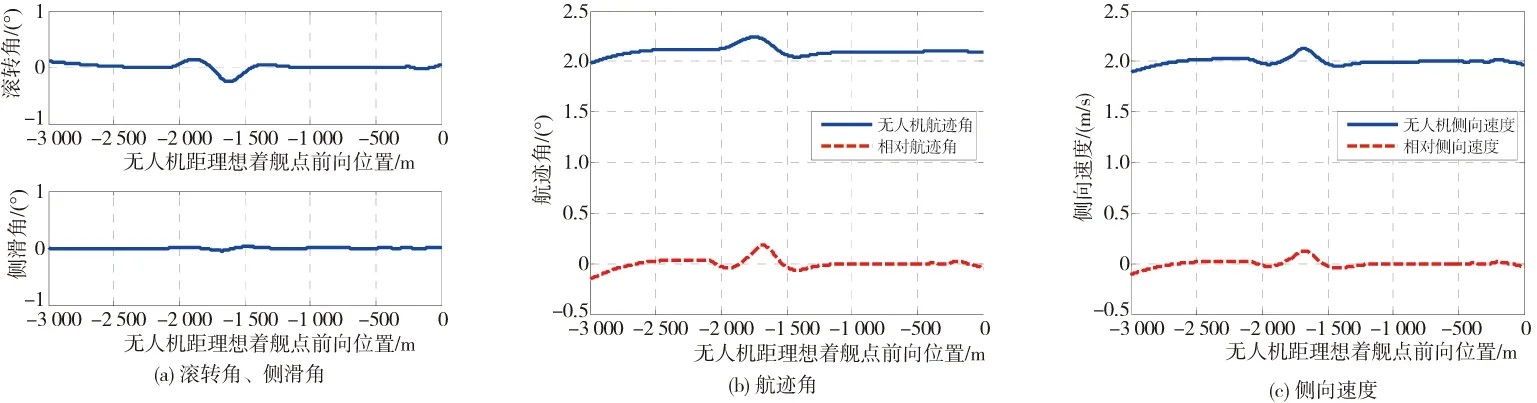
圖12 平靜大氣環境下著艦滾轉角、側滑角、航跡角、側向速度曲線

2)穿越艦尾流著艦仿真

為驗證本文設計的控制器在艦尾流影響下的控制效果，在仿真系統中加入了艦尾流模型；仿真采用的艦尾流模型為MIL-F-8785C軍用規范中規定的艦尾流[11]。

從圖13可以看出，艦尾流對無人機的橫側向軌跡跟蹤影響甚小。整個著艦過程中無人機與艦船保持了同樣的側向移動速度，側滑角控制基本為0，側向位置跟蹤誤差控制在±0.6 m內，實現了橫側向無側滑、無側向偏差的跟蹤控制。

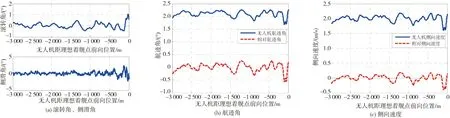
圖13 穿越艦尾流下著艦滾轉角、側滑角、航跡角、側向速度曲線

6 結語

本文針對艦載無人機著艦過程中姿態與空速控制問題，首先設計了航向增穩控制律，解決了橫側向荷蘭滾模態不穩定的問題；其次基于自適應動態逆理論設計了滾轉角控制律，使滾轉角控制變得準確、穩定；最后設計了以航跡角控制器和側向速度控制器，實現了平動軌跡的精確跟蹤。

仿真結果表明：該控制方法可以滿足著艦落點誤差的要求，且對艦尾流有一定的抑制效果，對著艦研究具有一定的參考價值。