基于遺傳算法的機器人加工位姿優化研究

王昊，張得禮，王宏濤

(南京航空航天大學 機電學院，江蘇 南京 210016)

0 引言

工業機器人由于其工作靈活、可移動和高重復定位精度等特點被廣泛應用于搬運、噴漆、銑削、焊接、制孔等工業加工領域。工業機器人與CNC機床一樣具有多軸功能，然而由于工業機器人獨特的懸臂梁結構，與CNC機床相比剛度相對較差。CNC機床的剛度通常>50 N/μm[1]，而工業機器人的剛度僅為CNC機床的1/50～1/20，提高工業機器人的剛度對提高加工質量具有重要影響。工業機器人末端剛度由機器人關節剛度和機器人位姿決定[2]，所以對于型號已定的工業機器人，其位姿對末端剛度有著決定性作用。此外，機器人傳遞力和運動的運動學性能、規避奇異點的能力對機器人的加工性能也有較大影響[3]。國內外學者有關研究表明，可以通過尋優機器人加工位姿達到提高機器人末端剛度性能和運動學性能的目的。CHEN S F等建立了工業機器人末端剛度和關節剛度、機器人姿態的關系，并表明末端剛度隨機器人姿態變化而變化[4]；ZARGARBASHI S H H等人提出一種與任務相關的優化方法，對機器人姿態進行尋優，從而選取滿足任務要求的最優加工姿態[5]；KHAN W等人基于機器人運動性能評價指標，研究了機器人不同運動性能對機器人加工軌跡的影響[6]。然而上述優化方法僅考慮優化機器人的剛度性能或機器人的運動性能，并沒有將二者綜合考慮。LIN Y等人在對機器人加工位姿的優化時，對機器人的運動性能和剛度性能皆進行了研究，但其選擇優化位姿的方式是在性能分布圖中直接選擇機器人關節角，未使用優化算法[7]。

本文基于機器人性能指標并結合遺傳算法對機器人加工位姿進行優化。

1 機器人運動性能對加工位姿的影響

1.1 機器人正運動學模型

埃斯頓ER30機器人為六自由度關節式工業機器人，且所有關節均為旋轉副。按照D-H參數法建立機器人D-H參數模型如表1所示。表1中，關節1-6分別代表機器人的6個關節；θi為關節i的關節角度；di為關節i的偏距，即連桿i-1與連桿i的距離；αi為關節i-1與關節i軸線之間的夾角；ai-1為關節i-1與關節i軸線之間公法線距離。

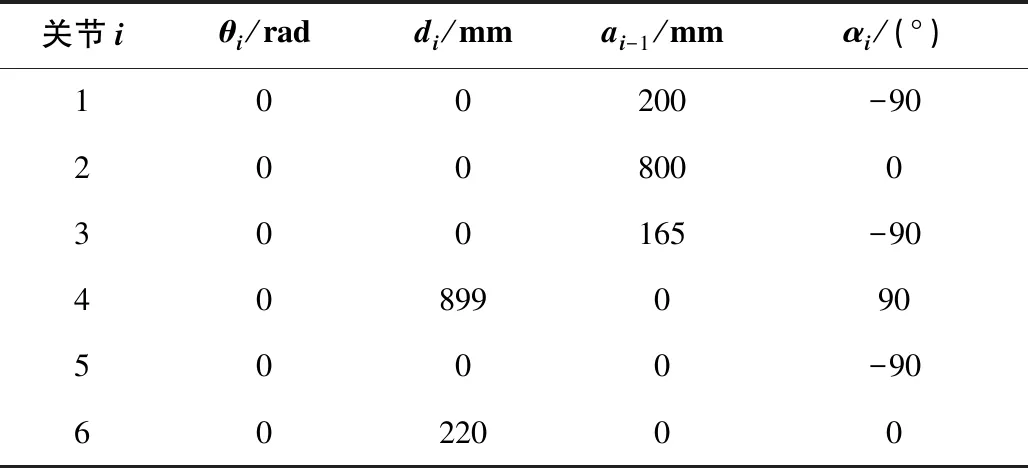
表1 ER30機器人D-H參數

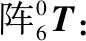
(1)

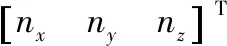
1.2 機器人運動性能評價指標

機器人運動性能是指機器人系統傳遞力和運動的能力，機器人的運動性能可以通過運動性能指標來評價。機器人運動性能指標除了可以評價機器人的運動性能還可以直觀地衡量機器人當前位姿與奇異點距離的遠近。本文選擇基于條件數[8]的機器人運動性能的評價指標，條件數定義見式(2)，機器人運動性能評價指標KM見式(3)。

(2)

KM=1/K(JN)×100%

(3)

式中：n為雅克比矩陣的維數，本文機器人為6R機器人，所以n=6；tr(JN)為機器人雅克比矩陣的跡；JN為雅克比矩陣的規范標準型。

1.3 各關節角對運動性能的影響

在機器人的6個關節角中，θ1、θ6對機器人末端運動性能無影響[7]，所以設置θ1=0,θ6=0，僅需研究θ2、θ3、θ4、θ5對機器人末端運動性能的影響。式(1)中機器人空間位置px、py、pz主要隨θ2、θ3變化而變化，機器人末端姿態n、o、a主要隨θ4、θ5變化而變化，所以可通過KM在2、3關節空間中的變化，研究機器人空間位置變化對KM的影響。通過KM在4、5關節空間中的變化，研究姿態變化對KM影響。

為研究θ2、θ3對KM的影響，通過蒙特卡洛法繪制KM在2、3關節空間的分布如圖1(a)所示。圖1(b)為機器人末端運動性能在笛卡兒空間的分布。在R1、R2、R3三個矩形區域中機器人的末端運動性能較好。通常情況下，機器人進行加工時，待加工工件放于機器人前方，所以當機器人進行加工時，機器人末端通常處在R1區域，此區域內的機器人加工位姿符合加工實際且機器人運動性能較佳，此時θ2∈[-1,0.5]，θ3∈[-0.8,1.5]。

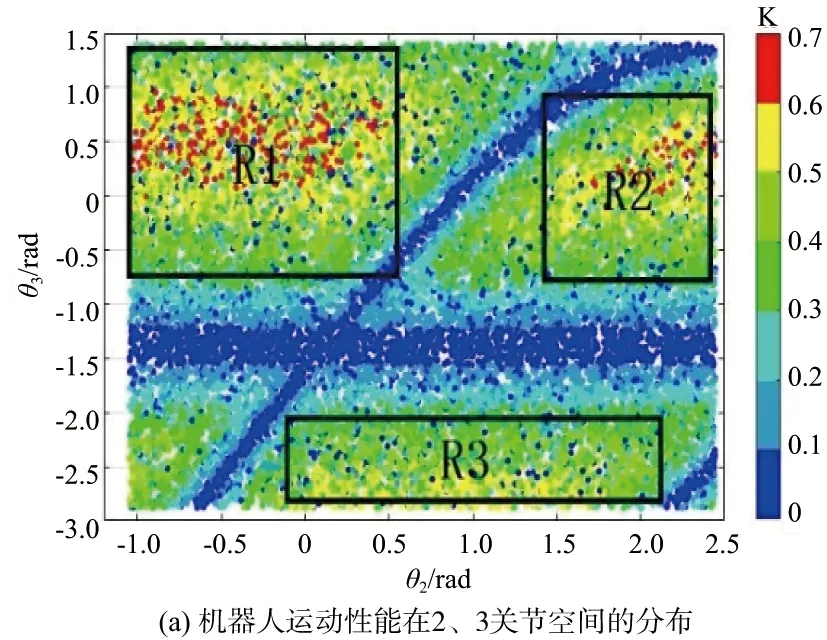
圖1 機器人運動性能在關節空間中的分布

同理，繪制KM在4、5關節空間的分布如圖2所示。由圖2可知，KM主要隨θ5變化而變化。在考慮姿態對KM的影響時，只需優化θ5的取值，以避免機器人四軸與六軸平行導致接近奇異點，機器人末端即可達到較好的運動性能。

圖2 機器人運動性能4、5關節空間中的分布

綜合上文分析，當機器人四軸與六軸不平行遠離奇異時，θ2、θ3變化導致的KM變化范圍為[0,0.7]，θ4、θ5變化導致的KM變化范圍為[0.5,0.7]。機器人末端運動性能主要受機器人位置變化即θ2、θ3變化的影響，機器人姿態變化即θ4、θ5變化對機器人運動性能影響較小。

2 機器人剛度性能對加工位姿的影響

2.1 機器人靜剛度模型

對于6R串聯機器人，加工時其末端誤差主要來自于機器人關節的受力變形[9]。基于此可以建立機器人末端笛卡兒剛度矩陣K與關節剛度矩陣Kθ的映射關系[10]：

K=J-TKθJ-1

(4)

式中：J為機器人雅克比矩陣；Kθ=diag([Kθ1,Kθ2,Kθ3,Kθ4,Kθ5,Kθ6])，為機器人關節剛度矩陣。

由式(4)可知，機器人的末端剛度與機器人的雅克比矩陣J和關節剛度矩陣Kθ有關。機器人的雅克比矩陣J僅由機器人位姿決定，所以機器人末端剛度具有位姿依賴性。

2.2 機器人剛度評價指標

為減少計算難度和計算誤差，引入機器人柔度模型：

(5)

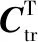
由于機器人末端所受力矩帶來的末端變形遠小于力帶來的末端變形。機器人末端的角位移也遠小于線位移，所以機器人剛度性能評價指標Ks可簡化為[11]

(6)

2.3 各關節角對剛度性能的影響

由參考文獻[7]可知，θ1、θ6對機器人剛度評價指標Ks無影響，設置θ1=0，θ6=0。機器人剛度性能在2、3關節空間的映射如圖3所示。對比圖3(a)和圖3(b)，當θ4、θ5變化時，機器人末端剛度性能在2、3關節空間的分布基本不變。當機器人運動性能較好，即θ2∈[-1,0.5]、θ3∈[-0.8,1.2]時，由圖可知，機器人的剛度性能在θ2→0.5，θ3→-0.8時較好。

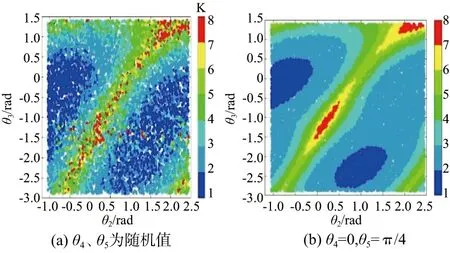
圖3 2、3關節空間的機器人末端剛度性能

圖4為機器人末端剛度性能在機器人4、5關節空間中的映射。由圖4可知，當θ2、θ3為隨機值時，機器人剛度性能的分布并無明顯規律；θ2、θ3為固定值時，機器人剛度性能分布呈現明顯規律，此時Ks取值區間為[2,4]。結合圖3，無論θ4、θ5為何值時，機器人剛度性能分布規律不變，Ks取值區間為[1,8]。由此可知θ2、θ3對機器人剛度性能有較大影響，θ4、θ5對機器人剛度性能影響較小，即相較于機器人末端的位置變化，機器人末端的姿態變化對機器人剛度性能影響較小。

圖4 4、5關節空間機器人末端剛度性能

3 基于遺傳算法的機器人加工位姿尋優

根據上文的分析，可以歸納得到機器人加工位姿優化問題的數學模型，如式(7)所示。這是一個多目標、多約束且目標數學表達式不可導的優化問題，解決此優化問題需要在變量全局范圍內對最優解進行搜索。遺傳算法對優化問題沒有太多數學要求，其較強的全局尋優能力的特點符合本文優化問題的要求。所以選用遺傳算法實現機器人位姿優化。

(7)

1)使用遺傳算法尋優機器人加工位姿需先設計變量和適應度函數，設置選擇、交叉、變異算子，設置終止條件，步驟如下。

步驟1：設計變量和取值范圍。機器人末端運動性能和剛度性能主要受機器人位姿影響，其中θ1、θ6對機器人末端運動性能和剛度性能均無影響，所以待優化變量為θ2、θ3、θ4、θ5。結合上文分析設置各變量取值范圍為：

θ2∈[-1,0.5],θ3∈[-0.8,1.2],θ4∈[-π,π],

θ5∈[-2.5，-0.5]∪[0.5,2.5]。

步驟2：設計適應度函數。適應度函數有兩個評價指標KM和Ks，以KM和Ks的和作為適應度函數。參考文獻[12]考慮到在加工時機器人的運動性能與剛度性能對加工效果都有明顯影響，設置權重ω1=2/3，ω2=1/3。最終的適應度函數如式(8)所示。

Fit(θ2，θ3，θ4，θ5)=0.000 1ω1Ks+ω2KM

(8)

步驟3：設置選擇、交叉、變異算子。使用輪盤賭選擇法對種群中的個體進行選擇。為快速淘汰低適應度值的個體，交叉方法為均勻交叉，交叉算子pc=0.8。變異算子pm通常在[0.001,0.1]區間取值，本文變異算子pm=0.05。

步驟4：設置終止條件。遺傳算法終止條件有多種，本文以達到目標代數作為終止條件，當迭代代數達到50代時停止優化。

2)完成以上設置后，使用遺傳算法對機器人加工位姿進行優化，步驟如下所示。

步驟1：生成初始種群。隨機生成符合取值范圍的25組關節角θ2i,θ3i,θ4i,θ5i(i=1～25)，并以二進制編碼的方式將25組關節角編譯成25個染色體作為初始種群。

步驟2：計算Fit。計算初始種群中25個染色體Fit(θ2，θ3，θ4，θ5)。

步驟4：判斷是否終止遺傳算法。若代數g<50，則g+1，進行步驟5；若代數g>50,則停止優化，輸出優化結果。

步驟5：遺傳操作生成下一代子群。根據當前種群中各染色體Fit值，對種群中所有個體進行選擇、復制、交叉以得到新的種群。進行步驟2。

運行遺傳算法得到的優化結果如表2所示。此優化結果對應的機器人位姿如圖5所示。優化位姿與隨機位姿的性能指標值如表3所示，相較于隨機位姿優化后的位姿各項性能得到了較大提升。

表2 遺傳算法優化結果(θ1、θ6=0)

圖5 優化后的機器人加工位姿

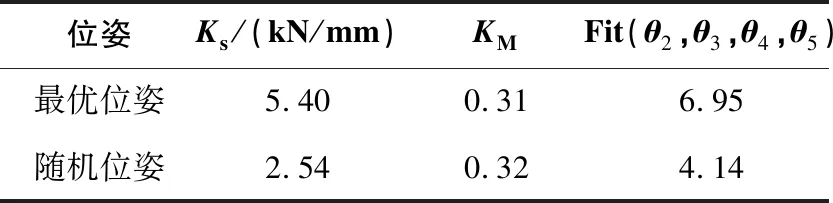
表3 優化位姿與隨機位姿的各評價指標值

4 結語

機器人6個關節中，θ2、θ3對機器人運動性能影響較大，θ4、θ5對機器人運動性能影響較小，θ1、θ6對機器人運動性能無影響。當θ2∈[-1,0.5],θ3∈[-0.8,1.2],θ4∈[-π,π],θ5∈[-2.5,-0.5]∪[0.5,2.5]時機器人運動性能較好且機器人位姿符合加工實際。

使用遺傳算法對加工位姿進行優化，設計了一種綜合機器人運動性能評價指標和機器人剛度性能評價指標的適應度函數，并通過系數設計調整兩種性能在優化過程中的比重，最終得到了一個符合加工實際且性能較好的機器人加工位姿。