考慮誤差的行星滾柱絲杠副嚙合模型研究

劉靖楠，范元勛

(南京理工大學 機械工程學院，江蘇 南京 210094)

0 引言

行星滾柱絲杠的結構組成包括絲杠、多個圓周布置的滾柱、螺母以及保持架等。與滾珠絲杠相比，行星滾柱絲杠同樣具有將旋轉運動轉化為直線運動的功能，且比滾珠絲杠具有更高的理論承載能力、使用壽命和使用可靠性[1-3]。但是與理論上的高承載能力相比，國產行星滾柱絲杠在實際使用上的表現不佳。影響行星滾柱絲杠承載能力的因素有很多，其中一個重要原因是由于滾柱制造安裝時存在精度誤差，導致滾柱各螺紋牙接觸程度不同，有些螺紋牙甚至沒有接觸，大大影響了行星滾柱絲杠的承載能力與使用壽命。因此，進行滾柱偏斜時的嚙合特性研究對提高行星滾柱絲杠副的承載能力與使用壽命有重要的意義。

目前，國內外對于行星滾柱絲杠的理論研究已有一定基礎，而國內的理論研究主要集中在運動學分析、軸向變形、動態特性以及傳動效率等方面[4-7]。在螺紋牙載荷分布方面，楊家軍等[8]依據Hertz彈性接觸理論，將滾柱作為整體，建立了剛度模型，得到了載荷分布與軸向剛度曲線;陳兵奎等[9-10]將滾動體等效成承受剪應力的矩形單元，建立了載荷分布計算模型并與有限元解進行對比。上述研究中，均假設行星滾柱絲杠副中的各滾柱的軸線與絲杠軸線平行，且各滾柱相對于理論位置未發生位移。

本文綜合考慮行星滾柱絲杠副在加工以及裝配過程中可能產生的各種誤差，建立了考慮誤差的行星滾柱絲杠副嚙合模型，并運用高斯牛頓迭代法進行求解，與其他論文模型進行計算結果比對驗證。結果表明：本文所提出的嚙合模型結果可行，可以有效地對行星滾柱絲杠副零部件加工誤差進行理論指導，為后續進行考慮誤差的載荷分布模型研究打下基礎。

1 行星滾柱絲杠副誤差描述與分析

行星滾柱絲杠副的工作原理與行星齒輪輪系原理相類似，其結構如圖1所示。

圖1 行星滾柱絲杠副結構

1.1 螺紋參數誤差

根據螺旋類零件加工誤差的分析，螺紋類零件加工誤差主要分為三類，即螺旋線分度誤差、螺紋中徑誤差以及牙型誤差。

1)螺紋中徑誤差

螺紋中徑是通過螺紋軸向截面內牙型上的溝槽和凸起寬度相等處假想圓柱的直徑，是確定螺紋幾何參數和配合性質的基礎參數。因此，螺紋中徑誤差是螺紋的一項重要技術指標。記中徑誤差為Δdi，其中i=s、r、n時分別表示絲杠、滾柱與螺母。

2)螺旋線分度誤差

理論上，多線螺紋的各條螺紋螺旋線間的相位角是相等的，但由于加工時分度機構自身的制造精度、零件熱變形以及操作誤差等因素，螺紋上各條螺旋線間的相位角將產生誤差值，如圖2所示。

圖2 螺旋線分度誤差

3)牙型誤差

牙型誤差的定義為實際牙型輪廓與理想牙型輪廓之間的差值。圖3中，虛線為理論牙型輪廓，實線為實際牙型輪廓，Δβi為螺紋牙側角誤差，Δci為螺紋半牙厚誤差，Δr為滾柱圓弧半徑誤差。

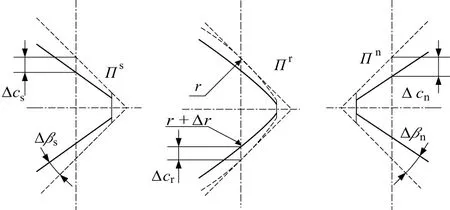
圖3 牙型誤差

1.2 滾柱定位誤差

1)銷孔定位誤差

銷孔位置偏差示意圖如圖4所示。

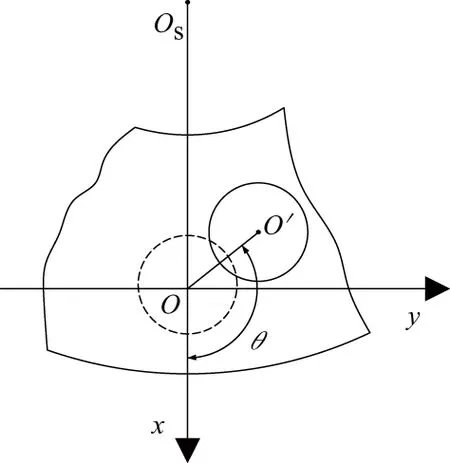
圖4 保持架中銷孔位置偏差示意圖

2)保持架定位平面誤差

定位平面誤差引起的滾柱軸向偏差示意圖如圖5所示。

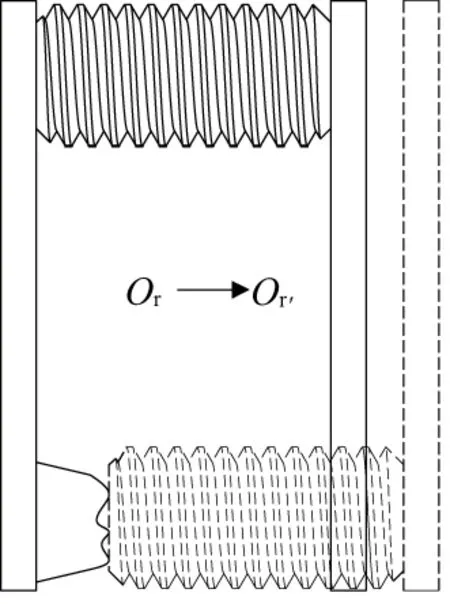
圖5 滾柱軸向偏差示意圖

3)保持架安裝扭轉誤差

安裝扭轉誤差引起的滾柱偏斜示意圖如圖6所示。

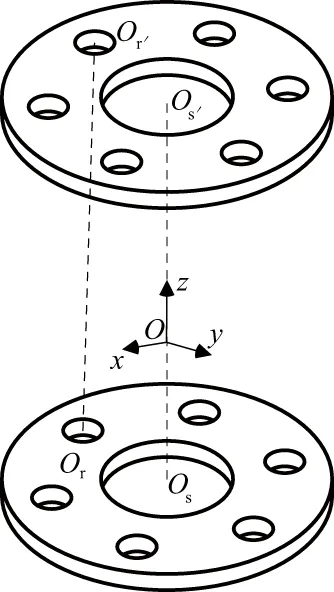
圖6 滾柱偏斜示意圖

2 行星滾柱絲杠副嚙合模型

2.1 考慮誤差的螺旋曲面方程

由于加工誤差的存在，行星滾柱絲杠副的滾柱在實際工作過程中存在著旋轉偏斜與位移偏斜兩部分。這兩部分偏斜參數，與前文所述各偏斜位移與中心線向量有關。行星滾柱絲杠副偏斜模型如圖7所示。

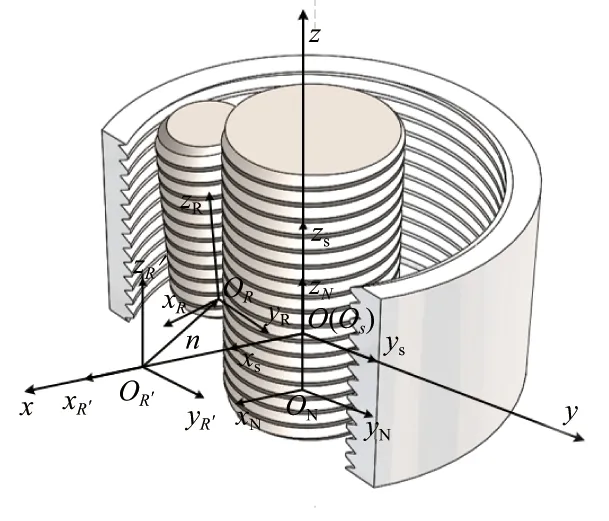
圖7 行星滾柱絲杠副坐標系

(1)

式中：OR′p為滾柱相對未偏斜坐標系的坐標；ORp為滾柱偏斜坐標系內的坐標；OR′ROR為滾柱相對于原坐標系的旋轉變換矩陣。

根據剛體轉動的歐拉定理，剛體有限轉動下的旋轉變換矩陣可表示其繞原坐標系各軸旋轉角度的余弦矩陣的乘積。因此，滾柱相對原坐標系的旋轉變換矩陣表現形式如下：

首先建立外螺紋的螺旋曲面方程。如圖8所示，在外螺紋坐標系中，取螺紋中徑上任一點O′，以O′為原點，垂直螺紋牙厚方向為x′軸,截面處與之垂直且與外螺紋軸線方向平行的另一坐標軸為z′軸，垂直截面的坐標軸為y′軸，以此建立相對坐標系。

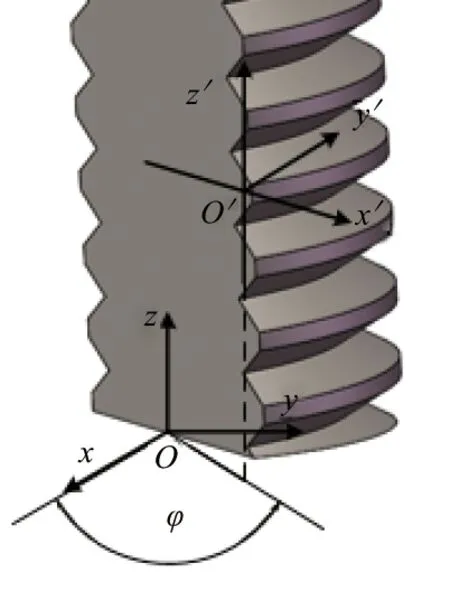
圖8 外螺紋相對坐標系

在坐標系O′-x′y′z′中，考慮誤差的外螺紋牙截面方程的表示形式為

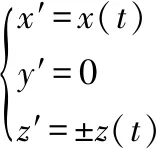
(2)

其中z的正號代表螺紋牙的上輪廓，負號代表下輪廓。

如圖8所示，參考坐標系O′-x′y′z′可看作將螺旋曲面主坐標系O-xyz將原點平移至O′后，坐標系繞z軸旋轉φ角而得到。其中φ為直線OO′在平面O-xy上的投影與x軸的夾角。因此坐標原點O′在主坐標系O-xyz中的向量參數為

(3)

式中：d為外螺紋的螺紋中徑；L為螺紋的導程；Δd為中徑誤差。

根據參考坐標系中的螺紋牙輪廓方程與參考坐標系與主坐標系的變化關系，可得外螺紋的螺旋曲面方程在主坐標系中的方程：

(4)

其中：OΠ為主坐標系下的螺旋曲面方程；OT為參考坐標系與主坐標系的變換矩陣；Π為在參考坐標系下的螺旋曲面方程。

(5)

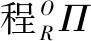
式中s、c分別為sin與cos縮寫。

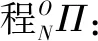
(6)

2.2 行星滾柱絲杠副嚙合模型

由于行星滾柱絲杠副的接觸類型為線接觸，因此，為了在安裝時便于裝配以及使傳動更加平穩，行星滾柱絲杠副的各螺紋間會留有一定間隙，因此可構建一個軸向間隙向量。根據嚙合原理的描述，在傳動過程中，兩相切嚙合點的法向量應保持平行，如圖9所示。

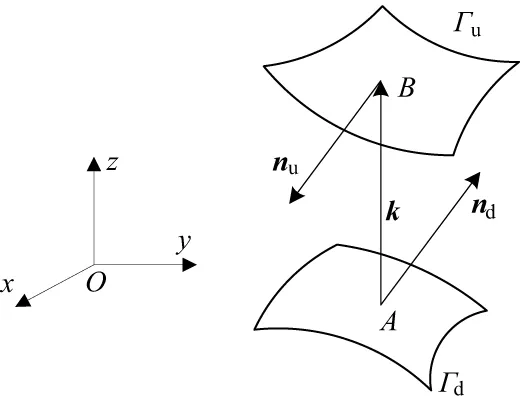
圖9 嚙合條件

圖9中，Γd與Γu為相嚙合的兩螺紋牙螺旋曲面,嚙合點分別為點A與點B，兩平面嚙合點處法向量分別為nd與nu，軸向間隙向量k=(0,0,δ)，則相切嚙合的接觸條件如下：

(7)

式中ξ為常數。

由式 (7)中的曲面與間隙方程，可得

(8)

通過式(7)與(8)可得出含有5個不同的未知數的方程組，此即為兩螺旋面間的嚙合方程，可求解相嚙合的兩螺旋曲面間嚙合與接觸參數。

螺紋分度后的螺紋牙螺旋曲面可看做原螺旋曲面繞z軸旋轉分度相位角后得到，左旋取正。所以，對于n頭絲杠與螺母來說，其螺紋分度矩陣為

(9)

將螺紋分度誤差帶入螺紋分度矩陣中，并將分度矩陣左乘絲杠或螺母螺旋曲面方程，可得改進后的絲杠與螺母的螺紋牙螺旋曲面方程。式中，j表示第j條螺紋線。將式(5)與式(6)左乘分度矩陣，可得出改進后的行星滾柱絲杠副的絲杠與螺母螺旋曲面。將求得的螺旋曲面帶入式(8)與式(9)中，即得出考慮誤差條件下的行星滾柱絲杠副嚙合方程。

2.3 模型算例驗證

為了與已有論文的計算結果作對比，以表1的標準式行星滾柱絲杠副螺紋參數為例進行嚙合方程求解運算。由于此計算未考慮任何偏斜誤差，故表中未標注的參數皆取值為0。

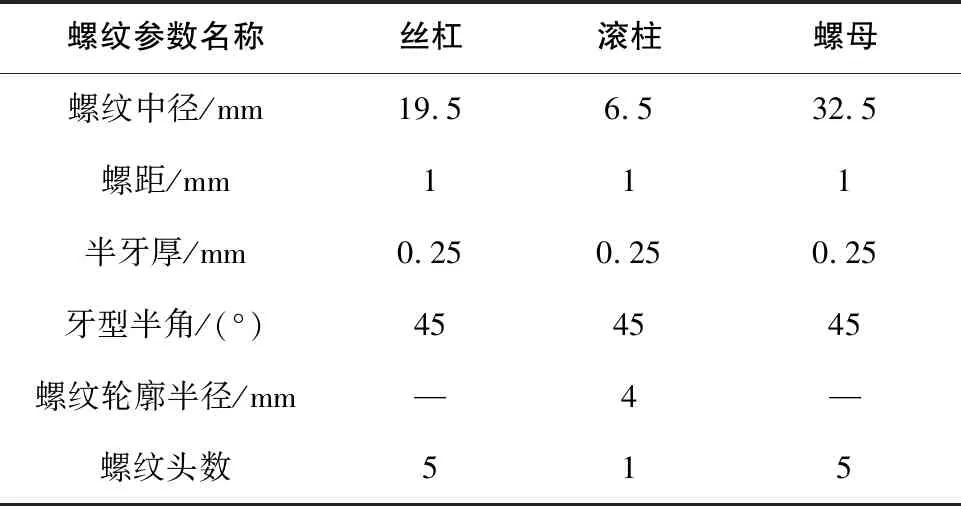
表1 標準式行星滾柱絲杠副螺紋參數

為了方便計算，選用x軸上的滾柱進行分析研究。在嚙合時，絲杠的分頭螺紋依次與滾柱螺紋進行嚙合。運用Matlab軟件進行迭代數值求解。取初值(0,0,0,π,0)，并設置終止條件ε=10-6，計算結果如表2所示(僅求解前5個螺紋牙的接觸參數)。

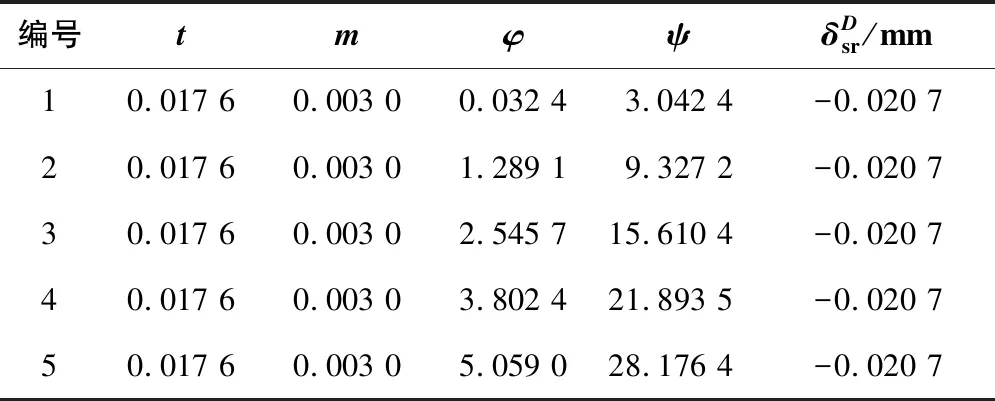
表2 滾柱絲杠側嚙合接觸特性計算結果

表中所求的軸向間隙與文獻[11]中的是一致的，說明本文所建立的螺旋曲面方程與嚙合方程在不考慮誤差的情況下是正確的。

通過在Creo中建立行星滾柱絲杠副模型，并觀察干涉量與間隙值，從而對考慮誤差的嚙合模型進行驗證。裝配模型如圖10所示。

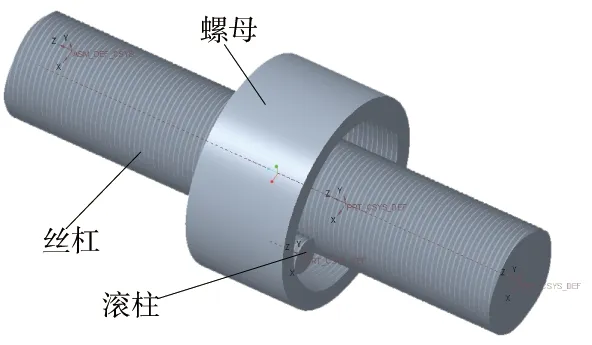
圖10 裝配模型

以絲杠螺紋中徑誤差分析計算為例進行驗證，將帶有絲杠螺紋中徑誤差的曲面方程帶入式(7)與式(8)中，計算不同誤差下絲杠與滾柱間的軸向間隙，同時建模分析三維模型的干涉量。計算結果如表3所示。

表3 不同絲杠螺紋中徑誤差下的計算結果對比

從表3中的干涉結果數據可以看出，隨著絲杠螺紋中徑誤差增大，Creo中三維模型的干涉體積開立方后的數據也將增大，其變化趨勢與本文所建立的嚙合模型計算出的軸向間隙變化趨勢基本一致，可說明本文所提出的考慮誤差的行星滾柱絲杠副嚙合模型是正確的。

3 結語

1)提出了一種考慮誤差的標準式行星滾柱絲杠副嚙合模型的分析方法，并經過算例計算三維模型驗證其結果合理，方法可行；

2)通過算例分析表明，當考慮誤差時，標準式行星滾柱絲杠副嚙合點將發生變化，可能影響行星滾柱絲杠副傳動精度及嚙合平穩性；

3)本文采用的分析方法假定各滾柱偏斜參數一致，會引入一定誤差；

4)本文采用的含誤差的嚙合模型分析方法可為進一步研究含誤差的行星滾柱絲杠副運動學與動力學分析打下基礎。