氣體在雙重多孔介質中運移的分數階導數建模研究

胡 韜 吳本霞 余星吉 靳 勇

(南京市江南小化工集中整治工作現場指揮部，江蘇 南京 210038)

在我國經濟快速發展和工業化進程不斷前進中，全球的能源如石油、煤和天然氣等占據重要地位，也是國民經濟發展的重要基礎[1]。隨著油氣工業的快速發展以及油氣資源的不斷消耗，非常規油氣資源如致密油、致密砂巖氣、煤層氣和頁巖油氣等正逐步取代常規油氣資源[2]。目前，隨著自然資源日益減少，環境污染與能源開采問題是能源可持續發展的兩大關鍵問題[3]，越來越受到整個社會的高度重視。眾所周知，雙重多孔介質系統如天然土壤、裂縫巖石、油氣儲藏、煤氣層等，其裂縫和基質孔隙自身結構具有不同的幾何特性。大多數油氣藏結構也是由多孔介質與樹狀分叉網絡鑲嵌而成的雙重多孔介質結構[4]。雙重多孔介質中的流體流動廣泛應用于水文、地質、石油工程、農業工程、環境工程等自然界和工業生產中，如地下水源污染預測、二氧化碳地下埋存和油氣資源開采輸運等，并越來越受到更多領域研究學者的高度關注和重視[5]。就當前研究現狀而言，研究較多的是地下水、污染物及溶質的運移過程，可為水污染預測及治理提供理論依據[6]。而在油氣開采運輸過程中，油氣儲藏存在分布范圍較廣、滲透性能較低和開采難度較大等特點，常用的注水驅替技術會損壞套管、發生水竄效應且采收率較低。而氣驅法最早源于1958年美國進行的注CO2混相驅項目；1996 年，美國又在圣胡安盆地 Burlington Allison試驗區進行了CO2驅替煤層氣現場試驗，并達到了提高采收率的效果。1963年我國將該技術引入到大慶油田；2003 年我國在山西的沁水盆地南部進行了CO2驅替煤層氣的單井試驗。此外，高等[7]利用不同高溫高壓實驗系統研究了CO2與原油相互作用的機理；黃等[8]建立了CO2驅替原油的多相滲流模型。總之，將CO2注入到油氣藏中，不僅可以實現CO2的地質封存，減少大氣中CO2的排放量，也可以降低油的粘度且提高油和氣的產量，從而達到提高油氣采收率和改善環境的雙贏目的[9]。因此本文主要關注氣體在復雜油氣藏中的運移過程，搞清氣體運移規律，對油氣勘探、開發都有重要的指導意義。

雙重多孔介質中的氣體運移過程由通過大尺度裂縫的滲流流動和基質內部的擴散運動兩種不同的物理機制構成[10]。Bear[11]第一個將對流—擴散方程(Convection-Diffusion Equation, CDE)模型用于描述宏觀多孔介質中溶質的運移過程。而在非均質土壤或儲藏結構中，由于流體自身特有的物理屬性和賦存壓力以及外界環境因素的干擾，使得流體流動出現反常擴散現象，即所測得的穿透曲線(Breakthrough Curves, BTCs)通常表現出早到達和明顯的長拖尾現象[12]，CDE模型無法充分描述該現象。本文引入了分數階導數模型的應用，分數階微分方程具有記憶性或非局部性，在工程、信息處理、物理、金融、流體等領域的應用越來越廣泛，比整數階微分方程能更好地模擬自然物理過程和動力系統過程[13]。2000年，Benson等[14]最早將分數階導數模型應用于地下水和溶質運移中，模擬Cape Cod實驗場地中溴離子的反常擴散現象；Meerschaert等[15]通過研究發現，初始階段污染物在土壤中運移的BTCs會出現提前穿透，而在運移后期會出現長拖尾現象。此外，Ali等[16]建立了用于描述致密介質中氣體運移規律的時間分數階對流—擴散模型。El Amin等[17]提出了空間分數階導數模型用于探討氣體運移過程。總之，目前研究高效開采油氣資源及突破技術瓶頸是學者們急需解決的科學和工程問題，而將力學、數學與石油工程、地球科學等學科實現深度交叉融合，可以更加有效地推動非常規油氣資源的勘探開發。

1 模型與方法介紹

1.1 分數階對流—擴散模型

從以往的研究中可知，對流—擴散方程可以準確地揭示流體在均勻多孔介質中的運移機理和時間、空間對運移過程的影響，同時還可以描述流體的反應擴散、質量分布和熱量運輸等物理現象，且形式簡單便于計算。通常用于描述均勻介質中的粒子運移問題的基本方程即經典對流—擴散方程，它的表達式如式1所示。

(1)

式1中C為濃度，v為平均流速，K為擴散系數。

在自然界和實際工程應用中，由于復雜多孔介質(土壤、裂隙巖體)結構和物理性質的非均勻性導致了反常擴散現象的出現，利用CDE模型描述氣體運移問題時存在不足。因為流體或粒子的運移過程是隨著時間、空間發生變化的，并不是恒定不變的。大量的實驗觀測和數值模擬結果也顯示氣體運移的濃度穿透曲線具有時間方向上的拖尾現象，和空間上的非高斯分布特征，而分數階導數算子具有歷史記憶性和空間依賴性，因此引入了分數階對流—擴散方程模型。本文主要開展了雙重多孔介質中氣體運移機理、運移模型、簡化求解、模型參數、模型應用以及運移規律等研究。

分數階對流—擴散方程模型的表達式如下：

(ⅰ) 時間分數階對流—擴散模型

(2)

(ⅱ) 時空分數階對流—擴散模型

(3)

這里α為時間分數階階數，β為空間分數階階數。

分數階導數的定義由時間或空間的非局部卷積算子表示，刻畫粒子反常擴散過程。常用的分數階定義包括Riemanm-Liouville、Caputo和Gründwald-Letnikov。下面簡要介紹幾種常用的分數階定義。

(ⅰ) Riemanm-Liouville定義[18]

(4)

和

(5)

(ⅱ) Caputo定義

(6)

(ⅲ) Grünwald-Letnikov定義

——法國農業部稱：預計2018年法國葡萄酒總產量為46.1億升，比2017年增長27%，超出過去5年平均產量達6%。在波爾多，盡管部分酒莊受到冰雹和霜霉病的影響，但預計產量還將達到歷史正常水平。

(7)

(8)

1.2 數值模擬方法

通常分數階微分方程的解析解含有特殊函數或者復雜的級數，難以獲得方程的解析解，因而數值求解方法引起了學者們的廣泛關注。多種求解對流—擴散方程的數值方法，如有限差分法(Finite Difference Method)、有限體積法(Finite Volume Method)、有限元方法(Finite Element Method)和無網格方法(Meshless Method)等被利用[19-21]。

本文主要采用的是較為靈活、簡便的數值計算方法，即有限差分法求解分數階微分方程，且求解分數階偏微分方程具有適用范圍較廣、精度較高和穩定性較好等特點。Liu等[22]建立了一種顯式差分格式求解時間分數階擴散方程，并證明了方法的穩定性和收斂性。Meerschaert和Tadjeran[23]利用有限差分法有效地獲得了分數階微分方程的數值解。此外，Chen等[24]也較好地將有限差分法應用于求解分數階對流—擴散方程中，且方法的穩定性和收斂性被有效地證明。丁志清[25]利用有限差分法求解了空間分數階導數方程，并進行了收斂性分析。本文采用隱式有限差分法建立數值求解方案，該方法的穩定性和收斂性已被證明，這里不再贅述，感興趣的讀者請參考文獻[26-28]。

2 數值模擬結果分析

近年來的研究發現，整數階導數的非線性和變系數模型能夠描述某些特殊情況下的反常擴散過程，但依然存在適用面窄、參數物理意義不清晰和長時間歷程模擬不準確等缺點[18]。本文引入分數階導數模型，并對其進行數值求解。將時間分數階導數項進行離散，可以寫成如下式9的形式[29]。

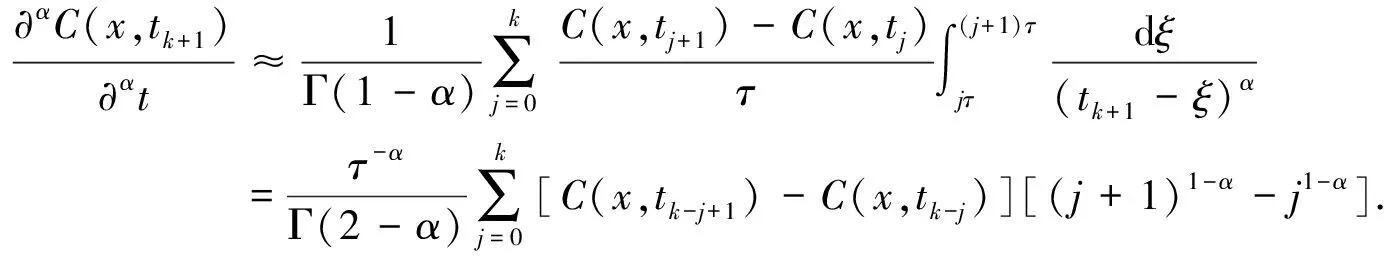
(9)

2.1 算例1

假設給定入口邊界處一個連續點源Cin且持續向模擬樣品入口端通入氣體，并在出口邊界定義了對流邊界條件，氣體濃度曲線呈不斷上升趨勢直至逐漸達到穩定。給出初始濃度值為0，且出口邊界條件設置為自由邊界條件。

通過數值模擬方法對氣體粒子在一定介質區域內的運移過程進行數值模擬，如圖1所示。

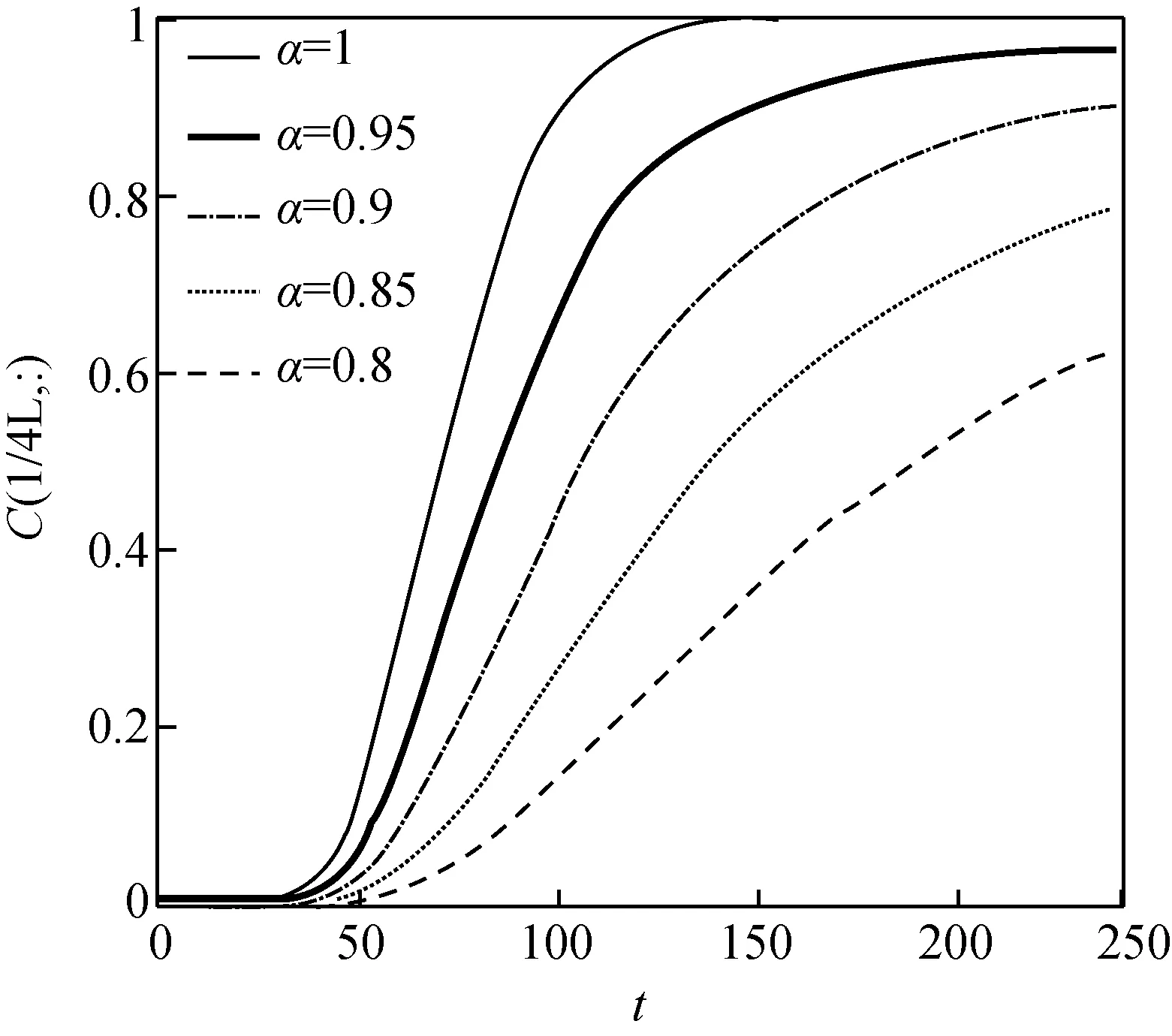
圖1 算例1：已知初始條件和邊界條件下，給定不同分數階階數α求解時間分數階對流—擴散方程(FCDE)模型在一定時間內模擬獲得的氣體粒子的幾種無量綱濃度穿透曲線。模型參數如下：v=0.2，K=0.05，T=240和L=120。

在非均勻介質結構中，分數階導數模型是模擬粒子反常擴散的有效工具。圖1顯示，時間分數階對流—擴散模型模擬結果中的分數階階數α越小，粒子運移過程越緩慢且濃度達到最大值所需的時間越長。結合模擬結果推斷，介質結構是影響濃度穿透曲線變化的主導因素，分數階模型中的階數有效反映了介質結構對粒子運移的作用。由于油氣儲藏基質具有較強的非均質性結構，雙重介質結構中存在死孔隙，或部分運移通道被阻塞、填充，這些都阻礙了氣體粒子的運移過程。從圖1可以看出，隨著分數階模型中的時間階數α變小，則顯示氣體運移過程越慢。而α=1時，經典對流—擴散模型在達到最大濃度之前以最快的增長趨勢變化，直至濃度達到峰值。

2.2 算例2

假定在入口邊界處給定一初始值為C0，而設置入口邊界條件為0，同時設置出口邊界為自由邊界條件。

分數階導數模型的數值模擬結果展示如下。

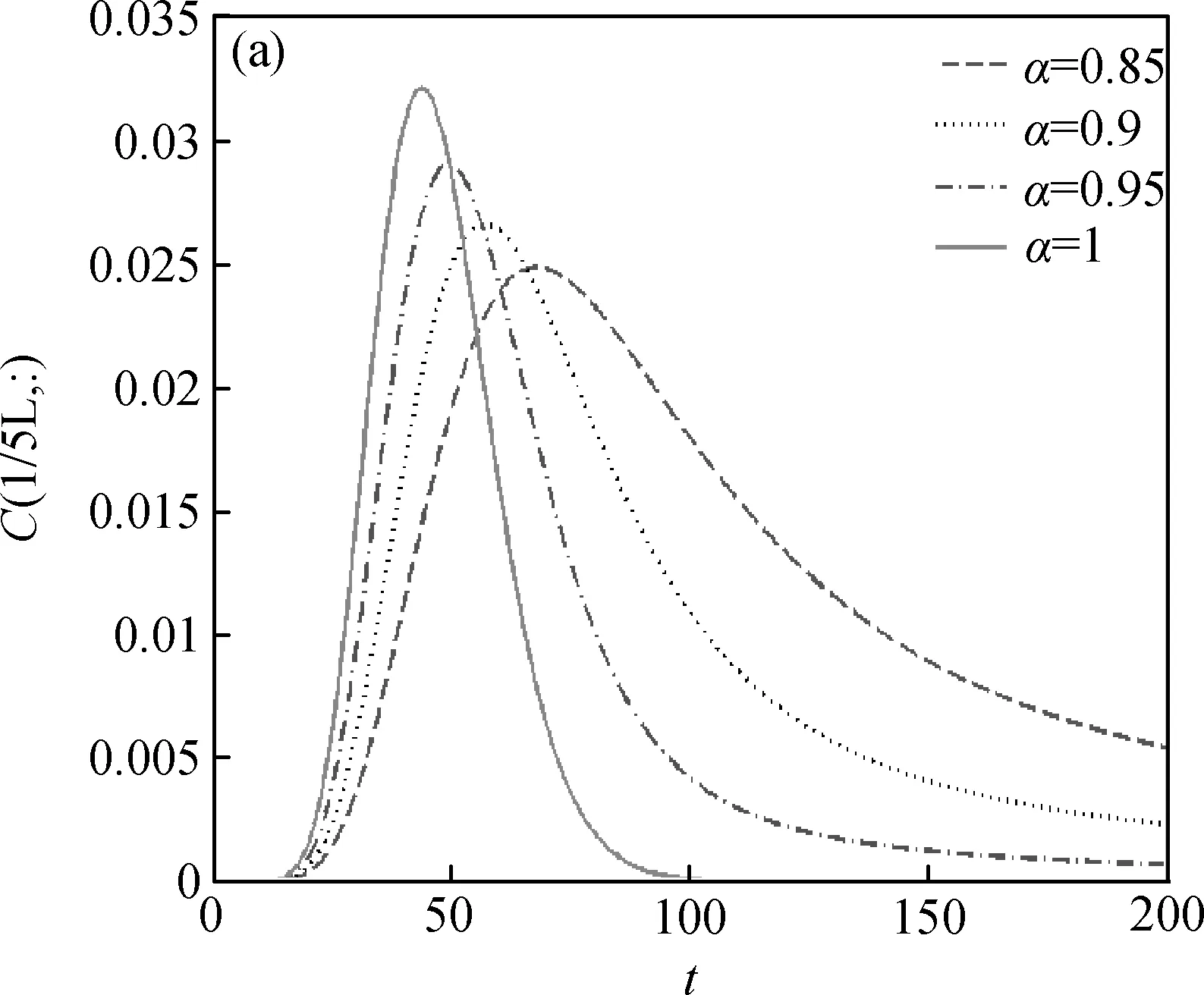
圖2顯示在時間分數階導數模型中，通過數值方法求得幾種不同時間階數α下的濃度穿透曲線。在分數階對流—擴散模型中，當0<α<1時，分數階階數α對氣體運移過程具有強有力的影響。在固定的控制位置1/5L處，隨著階數α的減小，濃度峰值越小，并且反常擴散會出現緩慢的衰減。圖2中可以看出濃度穿透曲線的尾部斜率隨階數α的改變而改變，階數越小，則冪律拖尾現象越嚴重，拖尾就越長，這是由于粒子運移通道被阻塞且阻礙了氣體的運動。圖2(b)是半對數坐標圖，可以觀察到不同時間階數α下，濃度穿透曲線的尾部斜率不同，說明了時間階數α是影響拖尾現象的主要參數。

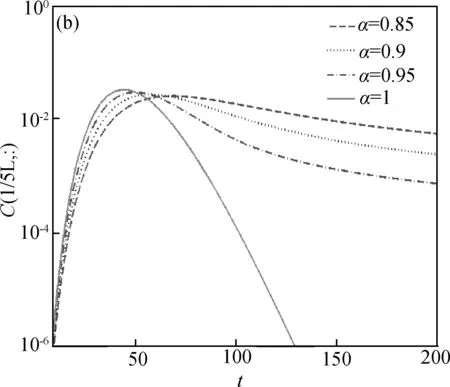
圖2 算例2：已知初始條件和邊界條件，由時間分數階對流—擴散模型數值求解獲得的不同階數α下的濃度穿透曲線(a)。模型參數如下：v=0.2，K=0.01，T=200和L=100。(b)是半對數坐標圖。

2.3 算例3

在邊界處給定一瞬時點源，利用時空分數階對流—擴散模型(3)模擬粒子運移規律。初始值為C0，入口邊界值為0，右邊邊界條件為自由邊界。數值模擬結果如下。

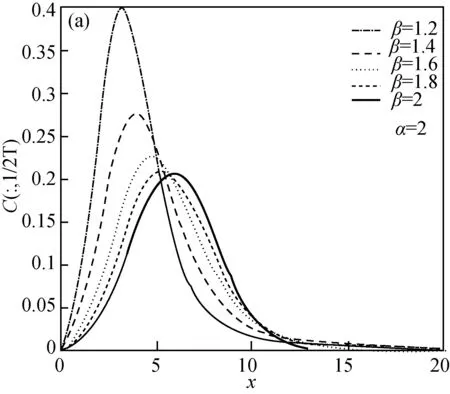
從圖3可以得出，空間分數階對流—擴散模型能夠較好地模擬粒子的早到達現象。隨著空間階數的減小，早到達現象越明顯。結合實際情況分析，若粒子在雙重多孔介質中運移時，介質中存在大尺度裂縫通道，促使粒子加速運動，因此出現了早期的超擴散現象。氣體在雙重多孔介質中的運移過程與孔隙結構和空間分布密切相關。簡而言之，分數階導數模型是描述具有記憶效應的氣體運移過程的有效工具，下面將通過實驗數據驗證該模型。

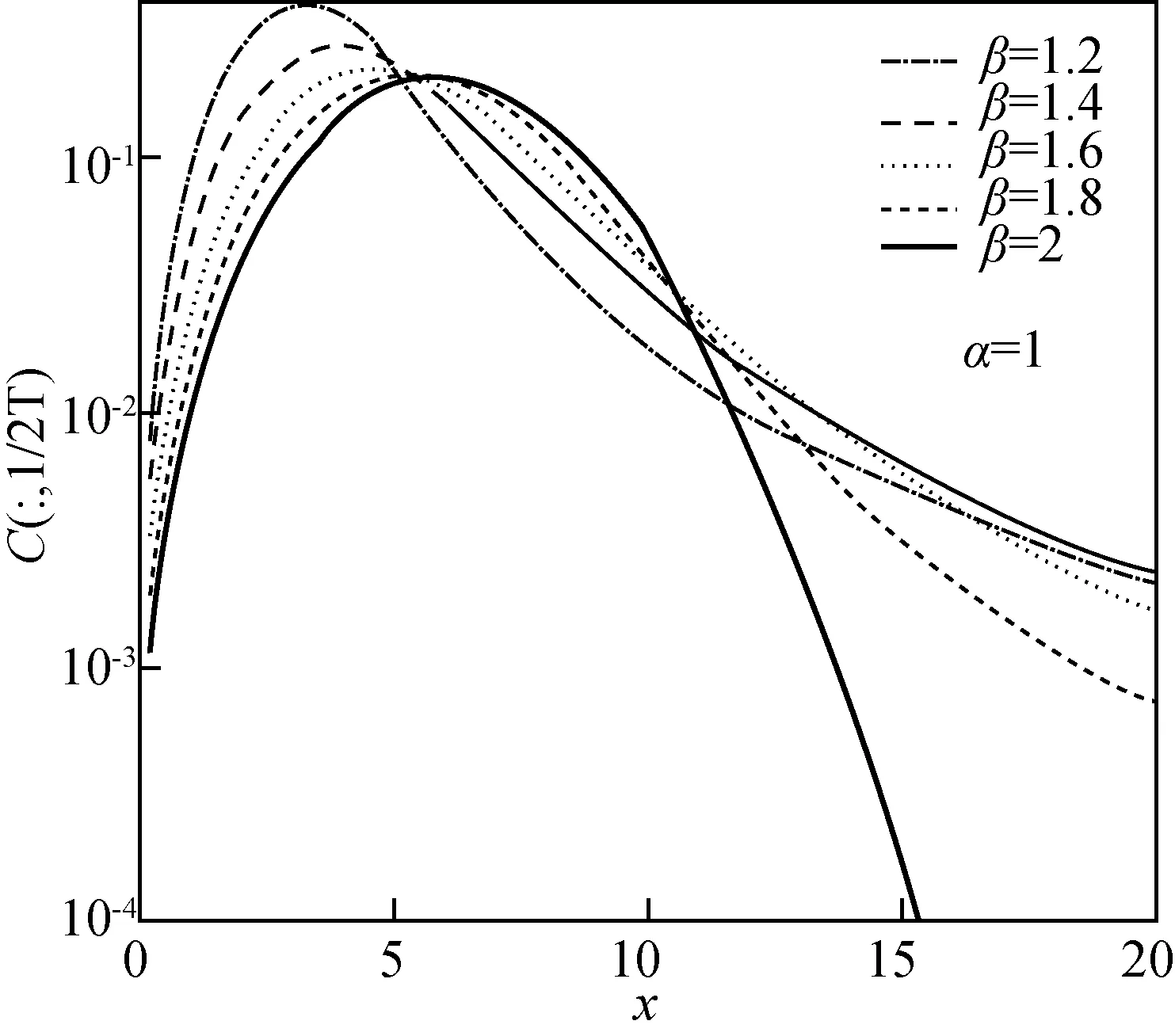
圖3 展示的是時空分數階對流—擴散模型模擬的數值結果(a)，(b)圖是半對數下的坐標圖。模型參數為：C0=20，v=0.1，K=0.05，T=200和L=20。

3 結果討論

基于文獻[30]中的一系列實驗研究，探討不同條件下包括壓力、溫度、氣體流速和介質不均勻性等，CO2驅替頁巖上CH4的動力學理論機制和CO2驅替的有利條件。經典對流—擴散模型在模擬CO2在頁巖儲藏的裂隙和基質系統中的傳質過程時，存在明顯不足。因此借助分數階導數模型研究氣體運移規律，模擬氣體的濃度穿透曲線。

在非均勻頁巖儲藏中，CO2置換CH4的過程較為復雜，CO2的運動會出現反常擴散過程，其本質是時間上有記憶性和空間上有非局域性的過程，而整數階導數極限定義具有局域性不能準確地描述這類反常擴散過程。從圖4可得出，分數階導數模型相比于傳統模型更具準確性和實用性。分數階對流—擴散模型能夠較好地描述驅替頁巖過程中CO2在非均勻儲層中的次擴散過程。分數階導數模型因其具有記憶和遺傳、路徑依賴性，能夠較準確地刻畫氣體粒子的反常擴散過程。

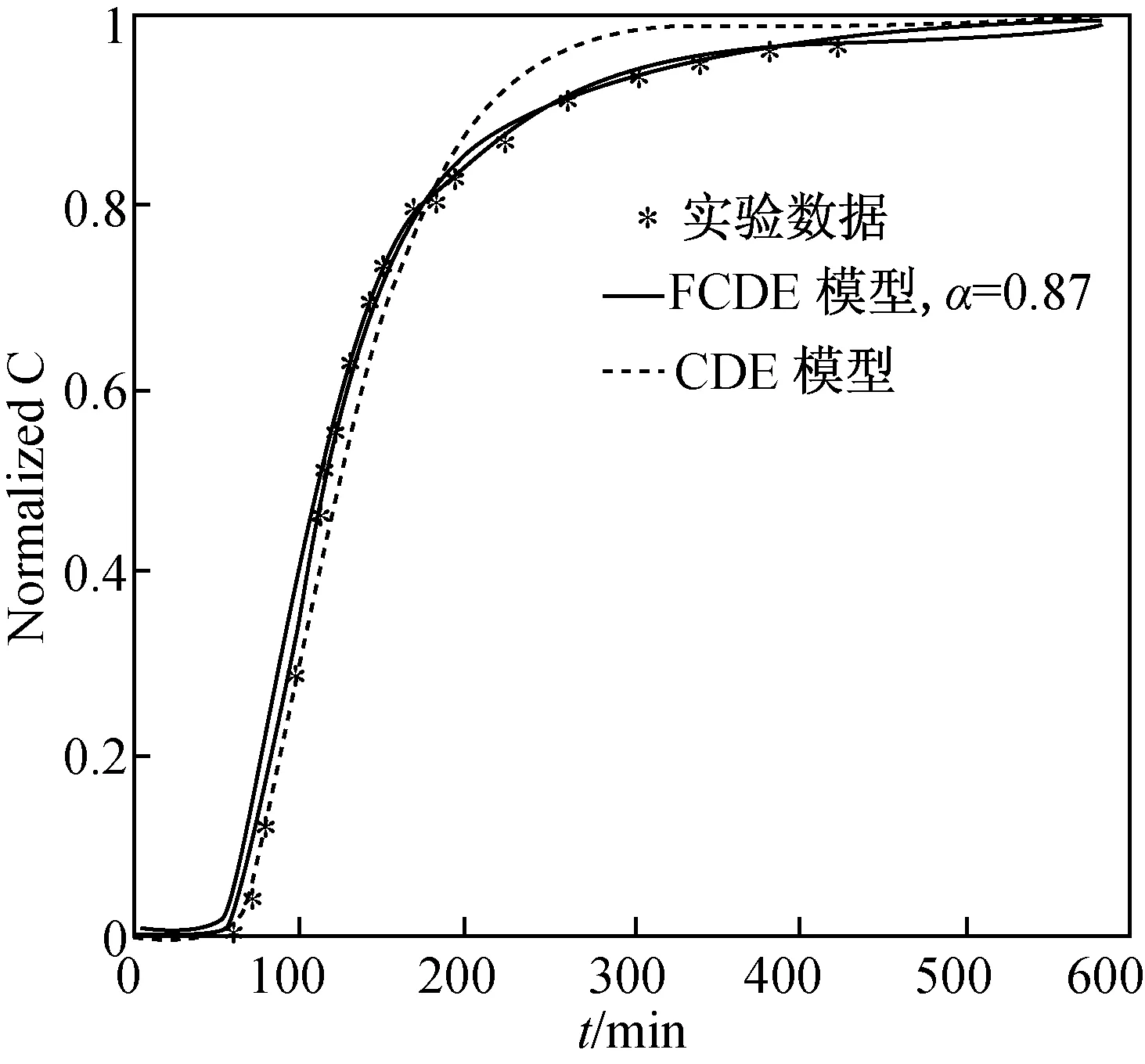
圖4 利用時間分數階對流—擴散方程(FCDE)模型和經典對流—擴散方程(CDE)模型模擬CO2的濃度穿透曲線。模型參數分別為：L=50 cm，K=10-4 cm2/s，v=0.15 cm/s。

4 總結

分數階導數是微分—積分形式表示的非局域性算子，能準確地刻畫復雜介質結構或流場中粒子運動的全域相關和歷史依賴性，已成為一種流行的建模工具。

分數階對流—擴散方程模型在描述地下含水層、河流、土壤和裂隙巖體等復雜介質中的流體擴散或遷移過程時，具有參數少、物理意義清楚和描述準確等優點。

從數值模擬結果得出，分數階導數模型能夠較準確地刻畫粒子的反常擴散現象，通過改變分數階模型中的時間或空間階數，則可反映不同程度的次擴散或超擴散現象。

從實驗擬合結果得出，整數階導數的局部極限定義不適合描述地質儲存中氣體粒子運動過程具有的路徑和時間依賴特征。而分數階導數模型能夠較好地擬合實驗數據，準確刻畫了氣體的運移過程。