一道平面解析幾何考題的探究之旅

張 淦 (浙江省新昌中學(xué) 312500)

之前筆者參與了浙江省“9+1”高二聯(lián)考命題工作,命制了一道直線與橢圓的問題,結(jié)果學(xué)生的解答情況很不好.今年,一次高二校考中使用了這個題目.盡管考試的對象變了,但測試的結(jié)果還是不理想.解答正確的學(xué)生寥寥無幾,絕大多數(shù)學(xué)生雖然思路正確,但普遍不能將解題過程進行到底.這說明學(xué)生對平面解析幾何的本質(zhì)認識不到位，對解析幾何中算法的設(shè)計、選擇、優(yōu)化能力偏弱.為此,我們針對此題進行了專題教學(xué),通過不同解題策略的探尋、實施、反思和比較，讓學(xué)生體會平面解析幾何的基本內(nèi)涵——傾向用代數(shù)的方法研究幾何問題[1]，在問題解決的過程中,根據(jù)幾何問題和圖形的特征,探索解決問題的思路,用恰當(dāng)?shù)拇鷶?shù)方法“解析”幾何的問題.

1 問題再現(xiàn)

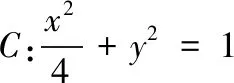
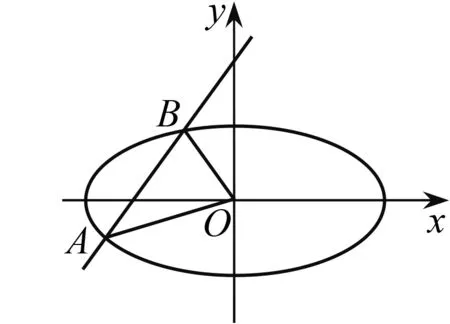
圖1

(1)略；

(2)設(shè)直線OA,OB的斜率分別為k1,k2,且k1=λk2,求實數(shù)λ的取值范圍.

2 解法探究

聯(lián)立直線l和橢圓C的方程,得到k的取值范圍.假設(shè)A,B兩點的坐標(biāo),利用兩點之間的斜率公式得到k1,k2的表達式,最終建立起λ與k之間的代數(shù)關(guān)系式.

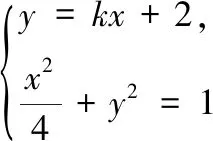
從解答過程來看,很多學(xué)生也是化簡到此,無法再繼續(xù)下去.究其原因,是式中的x1與x2不具有對稱性,無法直接使用韋達定理.因此①式的處理是整個問題的關(guān)鍵所在.

策略1 千淘萬漉雖辛苦,吹盡狂沙始到金——“直接法”

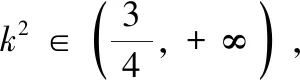
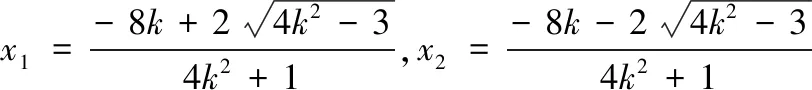
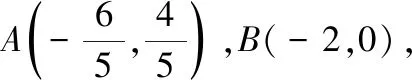
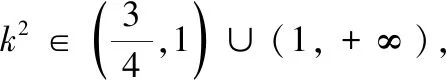
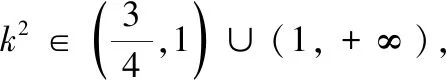
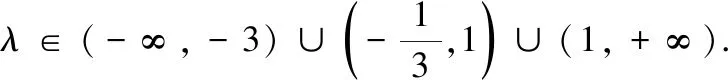
點評 我們在解題時,要理清題目的條件和需要解決的問題,明確問題和條件之間的聯(lián)系,看透問題的本質(zhì)，克服“怕運算”的心理障礙,不妨將自然的解題……