曲徑通幽 轉“角”尋蹤
——例析解析幾何“角”轉化的常用策略

福建省莆田第二中學 (351131) 黃少瑩

福建教育學院數學教育研究所 (350025) 蔡海濤

解析幾何是高中數學的主干知識，高考重點考查的內容.作為幾何定量問題中的重要元素“角”，是常見的考查載體，并且往往與三角函數、平面向量、平面幾何等相關知識交匯考查.如何轉化這些已知或求解(證)的“角”的信息，尋找適當的轉化途徑，是解決問題的關鍵.本文例析“角”轉化的常用策略.

一、利用斜率轉化

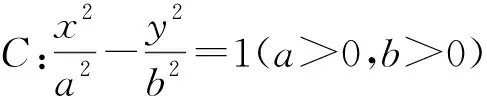
解：(1)易得e=2(過程略).

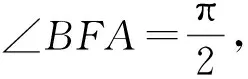
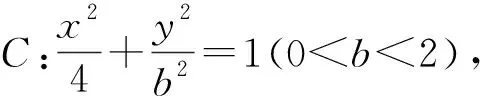
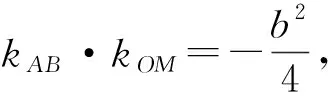
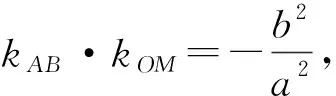
二、利用三角函數轉化

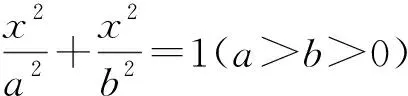
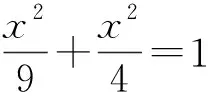
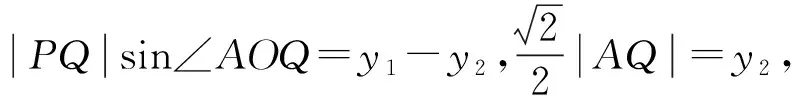
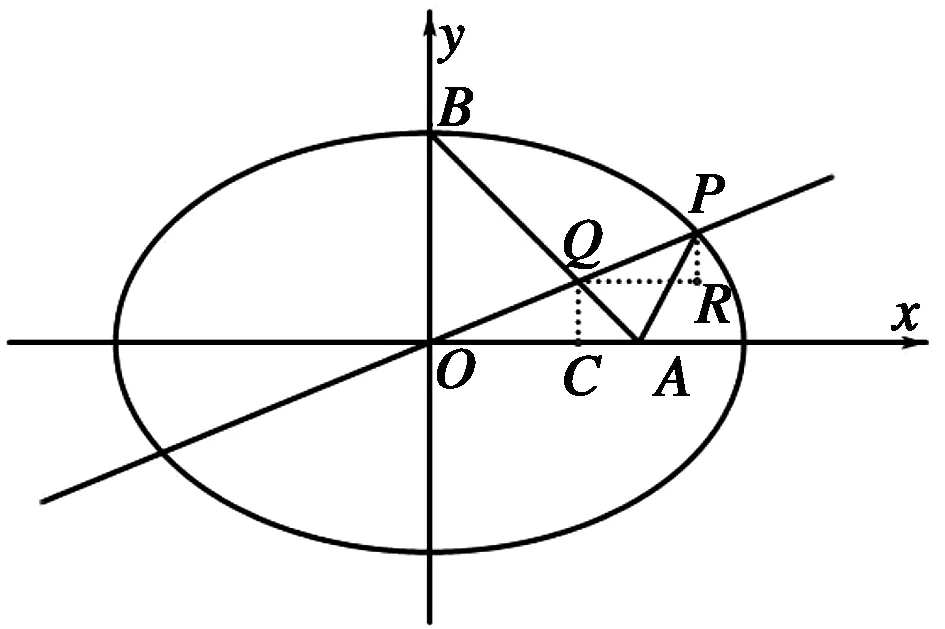
圖1

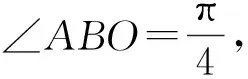
三、利用平面幾何性質轉化

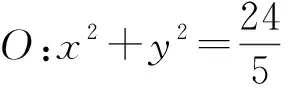
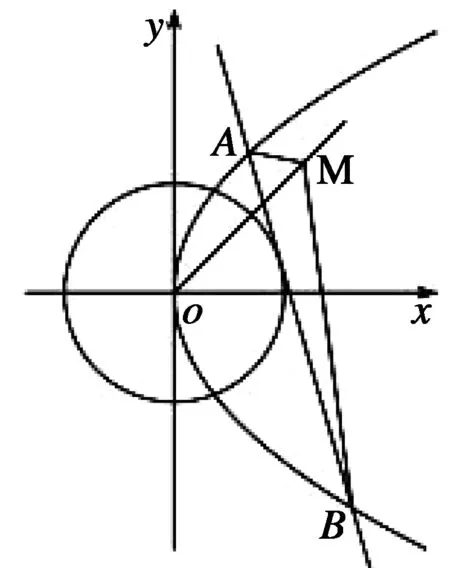
圖2

(1)求p的值；(2)求直線l的方程.

解：(1)易得p=2(過程略).

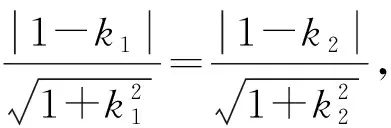
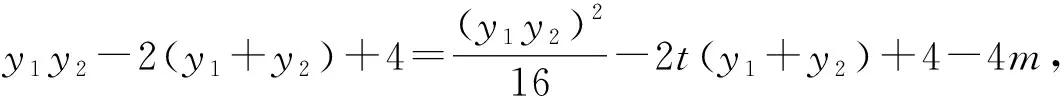
評析：由∠OMA=∠OMB知OM為∠AMB的角平分線，利用角平分線的性質得到點O到直線AM,BM的距離相等，從而得到k1k2=1，再將問題轉化至A,B兩點坐標，結合韋達定理進行解題.

四、利用平面向量轉化

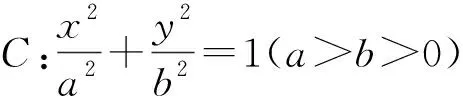
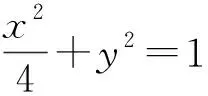
評析：由已知∠F1PM=∠F2PM，選擇結合點坐標利用向量的數量積求出cos∠F1PM與cos∠F2PM，由二者相等可以得到m與P點坐標的關系，從而求出m的取值范圍.

五、利用解三角形結合定義轉化

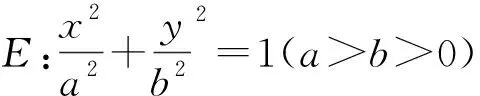
(1)若|AB|=4,△ABF2的周長為16，求|AF2|；

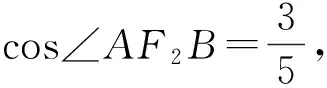
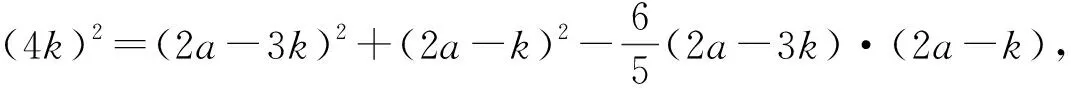
評析：本題先利用橢圓定義確定△ABF2的三邊關系，再利用余弦定理解決問題.當已知的角所在三角形與焦半徑有關時，可考慮聯系定義并結合解三角形進行轉化.

六、結語

“角”是描述圓錐曲線形狀特征的一個重要元素，它的變化直接導致曲線類型和形狀的變化.求解圓錐曲線“角”的問題，往往綜合性較強，是圓錐曲線教學中的一個難點，學生往往未能結合圖形特征，合理找到對“角”轉化的切入點來進行解題.教學中，教師可立足教材，聚焦高考試題，歸納通性通法，使學生感悟解決“角”問題的思想就是化歸與轉化的思想，轉化的途徑即從數從形這兩個角度來突破，鼓勵學生敢于思考，勇于挑戰，反思感悟，從而提升直觀想象與邏輯推理的數學核心素養.