2021年全國高考乙卷理科數學第12題解法探究
福建省莆田第二中學 (351131) 盧 妮
在近年高考試題中,比較大小問題,如2021年全國高考乙卷理科數學第12題,2020年高考全國卷Ⅲ理科第12題,2020年高考全國卷Ⅲ文科第10題,2019年高考全國卷Ⅰ理科第3題……,對學生來說是個不小的挑戰,得分率很低,這一現象引發筆者的思考.為什么學生的解答差強人意?是基礎知識薄弱、遷移能力不足、思想方法欠缺,抑或是應試心態緊張?本文從一道2021年高考題談起,研究這類問題的破解之道.
一、試題呈現

A.a 分析:本題考查比較大小問題,主要考查對數運算、對數函數的單調性、基本不等式等基礎知識,考查推理論證能力、運算求解能力、應用意識與創新意識,考查化歸與轉化思想、分類與整合思想,考查直觀想象、邏輯推理、數學運算等核心素養,體現綜合性、應用性與創新性. 評析:對于a與c,b與c的大小關系,根據泰勒公式將a,b,c展開估值可得出c與a,b的大小關系. 題1 (2019年高考全國卷Ⅰ理3)已知a=log20.2,b=20.2,c=0.20.3,則( ). A.a 分析:運用中間量0比較a,c,運用中間量1比較b,c,故選B. A.a 題3 (2020年全國卷Ⅲ理12)已知55<84,134<85.設a=log53,b=log85,c=log138,則( ). A.a 波利亞指出:“數學問題的解決僅僅只是一半,而更重要的是解題之后的回顧與反思.”本文中研究的題目考查比較大小問題,難度較大,關鍵難點是將各個值中的共同的量用變量替換,構造函數,利用導數研究相應函數的單調性,進而比較大小,這樣的問題,憑借近似估計計算往往是無法解決的.而高考鏈接題1-4不盡相同,但其題目背景都是以“對數式”為載體,解題目標均是“比較大小”,比較的方法均可利用“不等式傳遞性”,解題思想均是“化歸與轉化”.這啟示教師在解題教學中可通過一題多解,多個角度分析一道題目的思路,讓學生領會其中滲透的思想方法,積累解題經驗,達到“做一題、通一類”的效果.二、解法分析


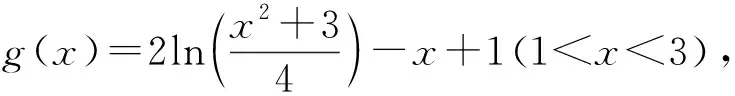
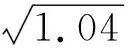
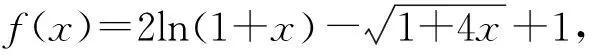
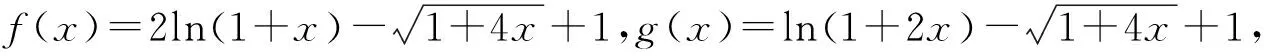
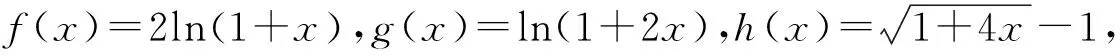
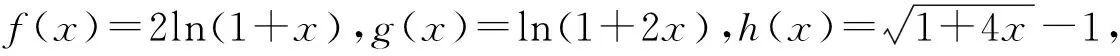
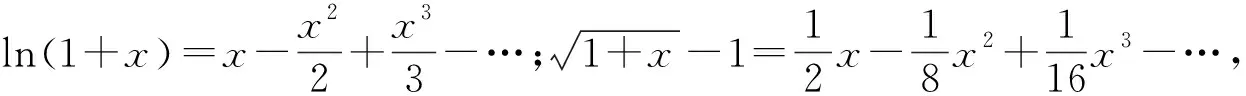
三、鏈接高考

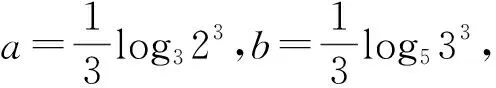

四、回顧反思

