一道橢圓試題的解法探究及推廣

貴州省六盤水市第二中學 (553401) 張 東

一、試題呈現

(1)求橢圓E的標準方程；

(2)過F2作兩條互相垂直的直線與E分別交于A，B和C，D,若M，N分別為AB和CD的中點.證明：直線MN恒過定點，并求出定點坐標.

試題評析：第(1)問以橢圓的基本概念入手，起點低，注重考查數學的基礎知識、基本概念，第(2)問考查直線與橢圓的位置關系、中點弦、定點問題.試題立足通性通法，注重數學本質，試題設計多層次，入口寬，解法多樣，考查學生數學運算，邏輯推理，直觀想象的數學核心素養，試題有很好的教育引導價值.

二、解法探究

這里我們只探討第(2)問,給出三種常見解法.

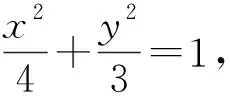
點評：聯立直線與橢圓方程，由韋達定理即可求出點M，N坐標，解法立足通性通法，淡化技巧，思路清晰明了，循序漸進，思維量小，但計算量大，學生需具備扎實的數學運算，邏輯推理素養，才能完備性地求出定點.

點評：從圓錐曲線點差法的思想角度入手，探尋動點M，N滿足的曲線方程(對稱中心不在坐標原點的橢圓)，直線MN恒過的定點即可轉化為學生熟悉的解析幾何問題.

點評：在解法二的基礎上，利用動點M，N滿足的曲線方程，另辟蹊徑，構造關于直線F2M，F2N的齊次化方程，引入韋達定理即可求出直線MN恒過的定點，該方法有一定的技巧性，可作為學生復習備考的選講內容，拓寬學生的解題思路.

三、問題一般化

由于試題中直線AB和CD的任意性，我們可把定點F2拓展到橢圓內部任意一點，得到問題的一般性結論，為了簡化證明，這里我們沿用解法三中齊次化[1]的方法給出證明過程.

四、問題推廣

五、問題引申

性質5 已知點P(x0,y0)為拋物線E：y2=2px(p>0)內部任意一點，過P點作兩條相交的直線與E分別交于A，B和C，D,且M，N分別為AB和CD的中點.若kAB·kCD=λ，則直線MN恒過定點

性質4、性質5證明過程可類比性質性質2、性質3完成，限于篇幅，這里不再一一贅述.